轮毂曲面机器人力控磨抛路径规划方法
2021-04-27王逸潇俞桂英郑建明
王逸潇,俞桂英,丁 烨,郑建明
(1.上海交通大学机械与动力工程学院,上海 200240;2.浙江万丰科技开发股份有限公司,浙江 嵊州 312400)
0 引言
汽车轮毂表面复杂,其磨抛工序以人工为主。由于人工成本较高,生产环境恶劣,工作强度较大,磨抛自动化逐渐成为研究热点。磨抛自动化中一大重要问题是磨抛路径规划。该路径不仅需要全覆盖复杂的轮毂表面,还应达到一定的磨抛要求,如磨抛量达到预期、磨抛效率较高等。因此,磨抛路径规划应考虑磨抛力学模型。由于恒定的力磨抛能够显著提高表面质量[1-2],所以越来越多的学者开始力控磨抛路径规划的研究。
力控磨抛路径规划首先需要获取轮毂信息,其方法主要有基于视觉[2]、基于三维扫描所得点云[3]、基于CAD模型[4]等。然后根据轮毂信息,规划全覆盖的磨抛路径。主流的复杂曲面全覆盖路径规划的策略是对曲面进行分割,对易于规划的子曲面进行局部路径规划,而后通过求解复杂的旅行商(TSP)问题来规划局部路径之间的间隔移动,以减少路径长度、提高效率[5-6]。曲面分割的目的是使得子曲面符合所选取的局部路径规划特性。2016年,Perez-imza等[7]选取zig-zag作为局部路径规划算法,使用正六边形进行曲面分割,在各子曲面迅速地计算出连续的局部路径。局部路径模式有2种:由平行线簇构成的类zig-zag路径[8-9];基于目标区域几何边界的轮廓或螺旋路径[10-11]。在考虑局部路径模式后,应引入制造工艺模型,以达到一定的制造工艺要求。2019年,Chen等[12]引入高精度磨抛工艺模型,通过规划进给速度使得工件表面各处磨抛去除量较为均一,从而提高磨抛表面质量。2011年,Li等[13]引入机器人机加工模型,根据去除量最大化等目标规划平行路径间隔。间隔移动算法主要是通过构建TSP问题,采用LKH[14]等算法进行求解[5]。
基于上述分析,针对力控轮毂磨抛,本文根据轮毂CAD模型采样形成的点云模型,设计了一套由基于扫掠线的曲面分割、考虑磨抛力学模型的局部路径规划、局部路径间的间隔移动规划构成的力控轮毂磨抛路径规划算法。
1 基于扫掠线的曲面分割
传统路径算法难以应对复杂曲面如轮毂的情况,在碰到凹区域或不必要加工的区域时,需要工具多次从工件表面抬起和落下,带来不必要的时间损耗。因此,有必要将复杂曲面进行分割成数个子曲面,使得在各个子曲面的局部路径能够连续,以减少刀具抬起落下次数。但若分割成的子曲面数量过多,在子曲面之间的间隔移动规划会更为复杂,反而会增加刀具抬起落下次数,影响加工效率。因此,本节提出基于扫掠线的曲面分割方法,使得子曲面内的任意平行扫掠线均可连续,且子曲面数量较少。
传统刀具路径是由一组平行的直线或曲线构成。该种刀具路径较为简单,易于实现,通用性较强,且适用于轮毂磨抛实际工况。可以通过莫斯分解(Morse Decomposition)[9]将复杂曲面分割成由不间断的平行线覆盖的子曲面。但该种方式需要确定分解函数以及区域边界的一、二阶导数等,在面对复杂几何区域时,实现较为烦琐。因此,基于莫斯分解的部分思想,提出了一种曲面分割的数值方法。该方法可人为设定任意平行曲线,适用于任何几何区域,其步骤如下:
a.设置平行线模式(空间中任意直线、曲线)与足够小的扫掠半径r,生成相邻间隔为r的n条扫掠平行线,使该线簇能够覆盖目标区域。每条平行线会和目标区域的边界相交,从而形成数条线段,记该线段集合为{li},i∈{0,1,2,…,n-1}。
b.对每个线段集合{li},i∈{0,1,2,…,n-2},检查每条线段与{li+1}中的线段是否有重叠。2条线段重叠定义为将一条线段沿法向投影到另一条线段,投影线段与另一条线段有重合。
c.将{l0}中的每条线段定义为一个子区域。

由此,可获得由线段构成的子区域。在该子区域规划由该平行线模式构成的刀具路径时,平行线均不会间断。
2 磨抛局部路径规划
磨抛局部路径规划的主要目的是使子曲面各处的磨抛深度达到预期且较为均一。由于采用力控磨抛,磨抛工具进给速度越小,在工件表面某处的驻留时间越长,磨抛深度越大。相邻平行路径的间距过小,则会容易产生过磨;过大,则会造成部分区域磨抛不足。因此局部路径规划应考虑磨抛力学模型,对磨抛工具进给速度及相邻平行路径的间距进行规划。
本文所研究的圆盘工具磨抛模型,如图1所示。{w}为世界坐标系。{c}为磨抛力为0时,圆盘与工件曲面接触点c的坐标系,原点为c,z轴与工件曲面在c的法向n一致,x轴在xw-yw平面投影方向与进给方向Pf一致。{d}为圆盘磨抛工具坐标系,圆心在圆盘底面中心,z轴为圆盘轴向,x轴指向接触点c。
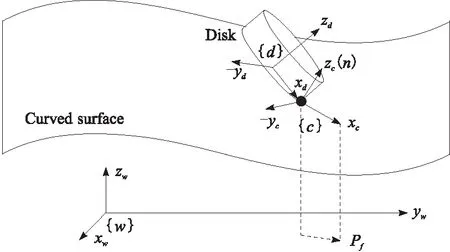
图1 圆盘工具磨抛曲面模型
2.1 接触力学及材料去除模型
根据接触力学[15],法向磨抛力F为
(1)
E为杨氏模量;H为圆盘磨抛工具的厚度;β为通过实验确定的系数;S为磨抛工具的磨抛区域(与工件接触的区域);s为其小量;h(s)为在s磨抛工具深入工件的沿磨抛工具轴向的深度。离散化后,法向磨抛力F为
(2)
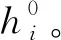
(3)
若给定法向磨抛力F,可通过牛顿迭代法计算h。 在某点的材料去除深度r为
r=Kpvδt
(4)
K为材料去除系数;p为该点所受压强;v为滑动摩擦速度;δt为磨抛时间。
2.2 进给速度规划
进给速度影响着磨抛量,也决定着是否发生过磨。进给速度越低,磨抛量越多,但由此可能会发生过磨。因此有必要进行进给速度的规划。
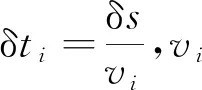
(5)
该优化问题可以通过线性规划求解,但没有考虑加速度约束。由于该问题是根据距离δs离散的,所以加速度可以通过式(6)求解:
(6)
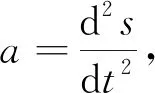
设最大加速度为Amax,则可用差分法计算得到加速度约束。对∀i∈{1,2,3,…,n-1},使用中心差分可计算得到加速度约束为
(7)
在首尾点采用前向差分和后向差分即可。
该问题可通过有约束的非线性优化算法,如Sequential Least Squares Quadratic Program-ming(SLSQP)等进行求解。
2.3 路径间距规划
路径间距规划的主要目的是使得路径间的平均残余磨抛量最小。设第i条与第i+1条平行路径的间距为xi,设第i条与第i+1条平行路径之间的区域为Area(xi),设区域Area(·)的平均残余磨抛量为MR(Area(·))。因此,已确定xn,对随后的m个路径间距进行规划的优化模型为
(8)
路径间距规划有2种策略:贪婪算法和全局算法。贪婪策略是当前已规划好前n条路径,并计算得到磨抛完这些路径后的子曲面内的残余待磨量,然后规划下一条路径的间距,即xn+1。根据xn+1可以确定下一条路径的各离散点,进而可以规划进给速度,从而获得子曲面内的残余待磨量,最终获得MR(Area(xn+1))。由于计算MR(Area(·))较为费时且难以计算梯度,采用全局求解器如模式搜索、模拟退火等可进行求解。全局算法是给定初始位置,同时规划m条路径。此时根据xn+1,xn+2,…,xn+m,可确定m条路径的离散点,进而可以同时规划这m+1条路径(包括初始位置)的进给速度,但目标函数替换为MR(Area(xn+1,xn+2,…,xn+m))。理论上,全局算法能够使得路径间的平均残余磨抛量更小,但所带来的弊端在于变量个数成倍数增长,求解效率降低,且容易陷入局部最优。
3 间隔移动规划
间隔移动规划是指已有局部磨抛路径后,如何规划磨抛工具在子曲面之间进行移动,使得这部分移动总耗时最少。一般来说,间隔移动总长度最短意味着总耗时最少。在之后的优化模型中,均采用使得间隔移动总长度最短为目标。值得注意的是,只要有计算总耗时的函数,即可替代总长作为新的目标。但优化模型的结构和方法均不变。
3.1 间隔移动规划变量
间隔移动问题的本质是将第i个子曲面的终止点和第i+1子曲面的起始点相连,并将第0个子曲面的起始点与工具初始位置点相连,∀i∈{1,2,…,n},n为子曲面个数,从而使得这部分移动总长最短。因此,各子曲面起止点的位置及连接子曲面的次序是决定总长的因素。
局部路径种类α决定了子曲面起止点的位置。由局部路径规划可确定不同间隔的平行线作为磨抛路径,但如何将平行线连成一条完整的连续路径具有4种可能性。图2展示了4种由竖直平行线构成的连续路径。其中连续段线为路径,箭头为进给方向。因此路径种类将影响起止点位置,从而影响间隔移动总长,是一个规划变量。
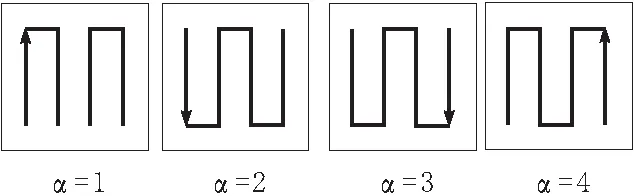
图2 4种不同的局部路径种类
连接子曲面的次序也将影响间隔移动的总长。在给定各个子曲面的路径种类后,将前局部路径的终止点和后局部路径的起始点两两相连的次序不同,间隔移动的总长度也会不同。
3.2 间隔移动规划问题生成及求解

s.t.αi∈{1,2,3,4},∀i∈{0,1,2,…,n-1}
(9)
这是一个非线性整数规划问题。遗传算法适合求解该问题[16]。
4 轮毂磨抛工艺实验
轮毂磨抛实验系统由ABB IR4400机器人、力传感器、电主轴、圆盘磨抛工具等构成,如图3所示。力传感器反馈力信息,以控制电主轴轴向的力恒定。测量系统为三维扫描仪ATOS-III,以确定磨抛前后轮廓误差。磨抛实验将磨抛由铝6061#制成的半个汽车轮毂模型。

图3 轮毂磨抛实验系统
根据研究所及企业经验、实验及测量结果,选取常用实验参数如表1所示。其中圆盘磨抛工具倾角ω指的是{c}沿yc旋转ω后得到{d}。实验所用砂纸目数为240#,半径与圆盘磨抛工具一致。

表1 轮毂磨抛实验参数
4.1 曲面分割及间隔移动实验
实验探究了曲面分割及间隔移动规划对磨抛效率的影响。对磨该实验不考虑磨抛量和表面质量,即不考虑局部磨抛路径规划。磨抛效率的评价指标为ABB机器人磨抛同一轮毂曲面总耗时。
实验圆盘磨抛工具中心磨抛半个轮毂上表面。假设局部磨抛路径间隔设为恒定的10 mm。磨抛力为12 N。设置磨抛工具与工件接触时的进给速度恒定为10 mm/s,磨抛工具从工件表面抬起并移动的速度为20 mm/s,磨抛工具移动至工件表面的速度为10 mm/s。图4展示了轮毂上表面及4种不同路径的垂直投影。实线为轮毂轮廓边界和磨抛工具与工件接触的路径,虚线为磨抛工具离开工件表面,移动至下一磨抛点。A为简单路径规划结果,B为进行曲面分割后的结果,C为进行曲面分割及间距移动规划的结果,D为将C的曲面分割扫掠线改成圆弧后的结果。表2展示了4种路径对应的区域个数、磨抛工具抬起次数(离开工件表面次数)、间隔移动路径总长度和总耗时。由于A没有进行曲面分割,故其没有区域个数。由A与B、C、D进行对比可得,曲面分割能够大幅减少磨抛工具抬起次数,降低间隔移动总长,从而大幅减小整体轮毂磨抛的耗时。由B与C进行对比可得,曲面分割及间隔移动规划能够将子曲面间的路径更好地连接起来,从而减少磨抛工具抬起次数,提高磨抛效率。由C与D进行对比可得,圆弧路径更适合轮毂磨抛。
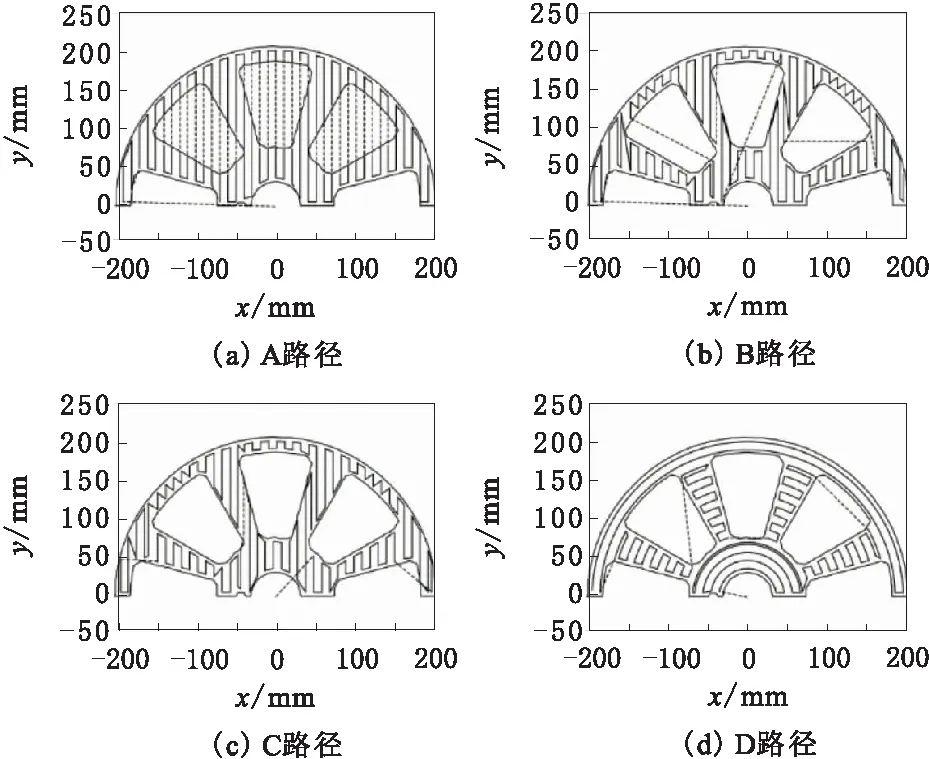
图4 4种不同的磨抛路径
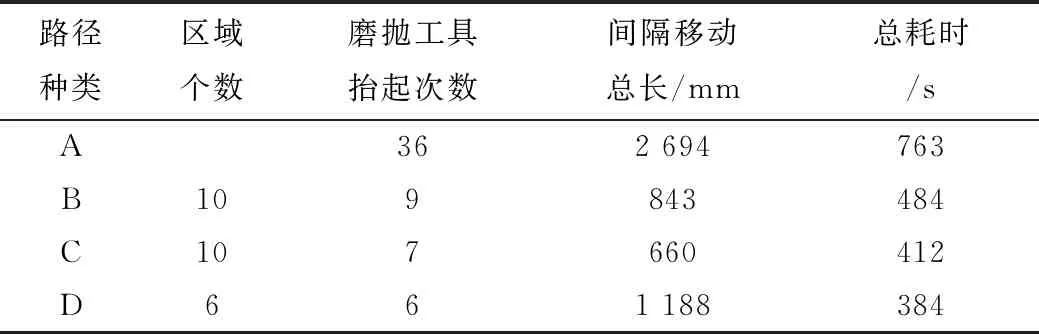
表2 实验结果统计
4.2 局部路径规划策略实验
实验探究了在局部路径规划中,贪婪及全局算法对残余磨抛量的影响。实验分别采用贪婪和全局算法规划3条平行路径,磨抛2根相邻的轮毂辐条。所采用的扫掠线形式为圆弧。磨抛力为8 N。预期磨抛去除量为80 μm,最大过磨量为20 μm,因此最大磨抛量为100 μm。磨抛前后分别使用三维扫描仪测量轮毂点云模型,对比计算得到材料去除深度,如图5所示。实验表明,相对于贪婪算法,使用全局算法能够显著降低表面平均残余磨抛量。
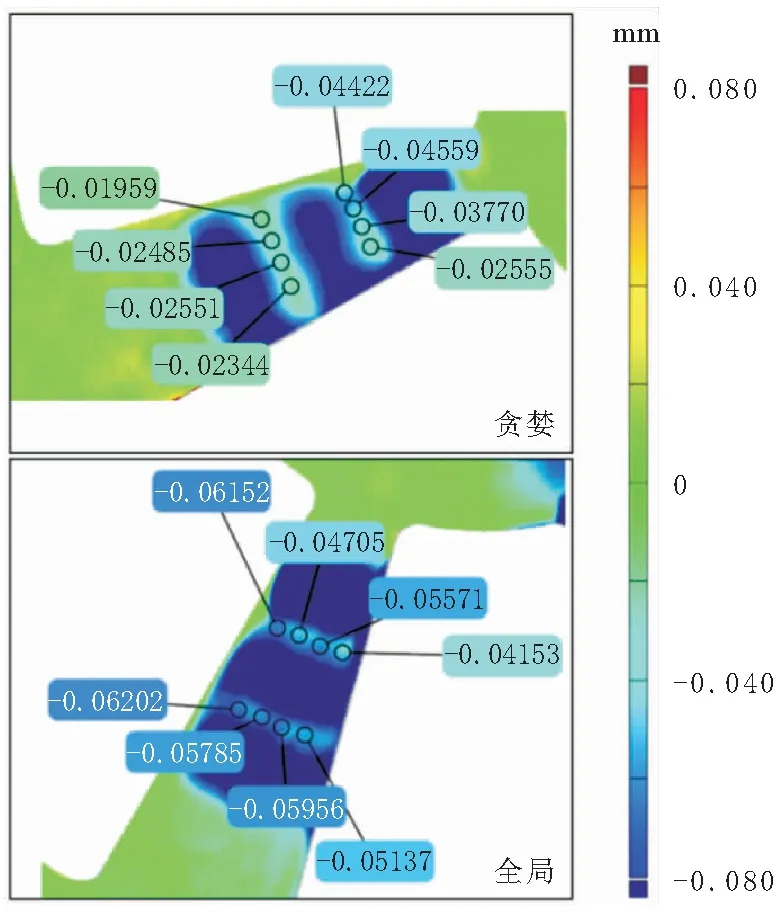
图5 贪婪及全局算法实验结果
4.3 轮毂整体磨抛实验
实验采用本文所提出的力控轮毂磨抛路径规划算法,磨抛半个轮毂上表面。所采用的扫掠线形式为圆弧。由于全局局部规划策略存在维度灾难,故采用更为稳定的贪婪策略。磨抛力为12 N,预期磨抛去除量为80 μm,最大过磨量为20 μm,因此最大磨抛量为100 μm。由于磨抛区域较大,为保持砂纸质量,每磨抛1块子曲面,更换1张砂纸。磨抛前后分别使用三维扫描仪测量轮毂点云模型,对比计算得到材料去除深度。
实验结果如图6所示。由图6a可以看出,磨抛后磨抛区域整体光滑、有光泽,磨抛效果较好。由图6b可以看出,大部分磨抛区域达到预期磨抛去除量80 μm,符合预期。部分区域达到去除量110~120 μm,略大于理论仿真计算。这是由于更换砂纸后,砂纸质量较好,材料去除系数略高于仿真实验参数。极少部分区域达到去除量140~160 μm。这与更换砂纸有关,也因为磨抛工具落下开始磨抛时,力控系统需要一定时间稳定,从而使得磨抛时间过长。
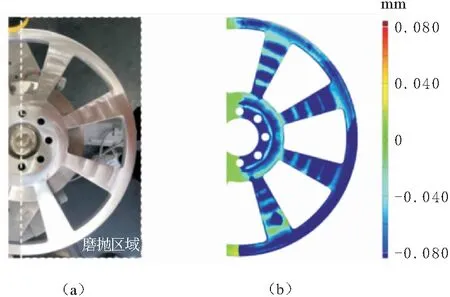
图6 轮毂整体磨抛实验结果
5 结束语
本文提出了完整的轮毂力控磨抛路径规划算法,并通过实验验证了其正确性及优越性。首先,根据局部路径模式,将复杂曲面分割成了数量较少的子曲面,从而使得各子曲面的局部路径能够连续且易于生成。其次,根据由接触力学和材料去除模型构成的磨抛力学模型,规划了路径各点的驻留时间及路径间距,使得子曲面平均残余去除量较小,并提高了磨抛效率。采用全局规划算法能够显著降低平均残余去除量,使得磨抛去除量更为光滑。最后,通过构建非线性整数规划问题,对各子曲面之间的间隔移动进行规划,降低了间隔移动的总长度。通过实验发现:
a.在磨抛中砂纸的损耗是磨抛量的重要影响因素之一。
b.子曲面相邻区域存在磨抛不足的情况。
c.全局策略存在维度灾难等。这些方向是未来值得研究的主题。
