双电机驱动的精密伺服转台及控制系统设计

段晓英，孙克龙，王雪芹

(中国人民解放军93498部队，河北 石家庄 050000)

0 引言

伺服转台系统作为雷达的重要组成部分之一，其主要功能是支撑和驱动天线运转，随着雷达应用领域的不断扩张和深化，对其伺服转台系统的要求也逐步提高[1]。然而，伺服转台系统中的机械传动装置通常采用齿轮或者蜗轮蜗杆等形式，存在着诸如齿轮侧向间隙、轴承间隙、弹性变形等各类影响传动精度的因素，严重降低了雷达伺服转台系统的动态精度和稳态性能[2]。同时，由于传动间隙的存在，在伺服转台启动或者换向的时候，会造成传动机构空回、齿轮组之间发生刚性碰撞等现象，不仅降低了传动精度，且容易产生振荡和噪声[3]。因此，减小传动间隙对于提高雷达伺服转台系统的控制精度和稳定性显得尤为重要。

为满足某雷达伺服转台高精度、高动静态特性的要求，本文从满足大负载、提高控制精度角度出发，立足于工程实际应用，采用机械消隙与伺服控制算法相结合的方式，提出在其伺服转台中采用双电机驱动的方式，并对整个机电系统进行详细的设计，最后利用MATLAB/Simulink对所设计的双电机驱动的伺服转台及控制系统进行建模和仿真[4]，以验证此系统设计方案的可行性，对实际系统的研制和调试具有十分重要的意义[5]。

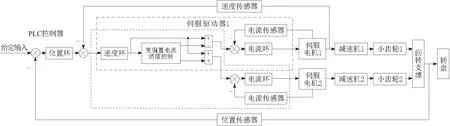
图1 双电机驱动的伺服转台及控制系统原理框图

1 主要指标要求

某雷达伺服转台的主要指标要求如表1所示。

表1 伺服转台主要指标要求

2 伺服转台总体设计

2.1 设计原理

为提高系统动态响应，同时减少传动链误差带来的影响，伺服转台采用双电机驱动的方式，实质就是用2台相同的电机分别带动2套完全相同的减速机构，再由2套减速机构的小齿轮带动主机构上的回转支撑转动。同时，2个电机按照设定的消隙控制算法运行，使得2个输出小齿轮分别贴紧在回转支撑的2个相反啮合面。此时，回转支撑无论是在启动还是换向的过程中，都将受到偏置力矩的作用，间接使其不能在齿隙中来回摆动，以此达到消除传动间隙，实现高精度控制的目的。

双电机驱动的伺服转台及控制系统原理框图如图1所示，系统收到输入指令后，由PLC控制器发出控制信号，经2个伺服驱动器处理后，按照设定的消隙控制算法驱动各个方位电机及减速机工作，同时通过同轴安装的高精度位置传感器采集角度信息并反馈给伺服控制器，以此实现伺服转台及控制系统的闭环跟踪功能。

2.2 设备组成

某雷达伺服转台主要由转盘、回转支撑、驱动单元、控制系统和旋转变压器等组成，如图2所示。

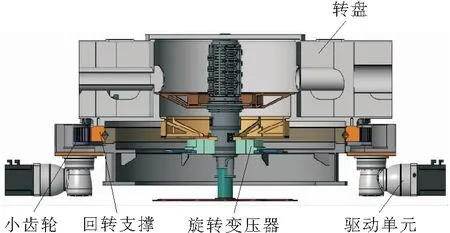
图2 伺服转台主要设备示意

转盘由高强度钢板和低合金结构钢拼焊成腔体式结构，内部布置相应的筋板，用于承载天线重量及天线阵面传递的环境载荷。

为了实现方位旋转运动，在一体化底座和转盘之间采用回转支撑连接形式。由于该伺服转台对跟踪精度要求高，因此选择精度等级为P4的回转支撑。

结合图2可知，转盘左右两侧的驱动单元结构形式完成相同，皆由伺服电机、减速机、小齿轮和安装板组成，其中小齿轮与回转支撑外齿啮合，齿隙通过调整安装板位置来调节，单侧末级传动链齿隙控制在0.15 mm左右。

控制系统由PLC控制器、伺服驱动器等组成，主要负责控制驱动单元中的伺服电机精准跟踪输入指令并形成反馈系统等。

旋转变压器是一种测量角度用的小型交流电动机，常用来测量旋转物体的转轴角位移和角速度。本文采用18位双通道旋转变压器来测量转盘的角位移、角速度等信息。

3 控制系统的设计与仿真

3.1 双电机驱动控制系统设计

除了在转台结构上考虑机械消隙之外，本文在控制系统设计中还考虑施加变偏置力矩的消隙控制方法。

如图1所示，本文所设计的双电机驱动伺服控制系统由电流环、速度环和位置环组成。电流环用于改善伺服转台的动态特性，速度环用于提高伺服转台的运行平稳性，位置环用于快速准确跟踪定位并实时反馈位置信息，三者共同实现伺服转台快速、精准的控制功能。

由于力矩正比于电流，所以施加变偏置力矩也就是施加变偏置电流。本文变偏置电流消隙控制模块采取如下方式：在2个电机原有电流环主输入的基础上额外叠加1个与2条支路相关的、幅值可调节的偏置电流，合成后的电流再送入各个电流环。整个伺服转台系统启动或者换向时，速度环的输出经变偏置电流消隙控制模块、电流环处理后，得到可调节的输出电流，又由于电流环输出电流与电机输出转矩之间呈线性关系，因而可使2个电机之间产生如图3所示的变偏置力矩，最终实现双电机同步消隙的目的[6-7]。

图4 双电机驱动的伺服转台及控制系统仿真模型

实际使用时，主要由PLC控制器、驱动器、伺服电机、减速机和旋转变压器等共同组成伺服硬件系统。本设计中，电流环和速度环均采用PI控制器，位置环采用带有前馈控制的PID控制器，将电流环和速度环均设置在伺服驱动器中，同时，在驱动器中引入如上所述的变偏置力矩消隙控制算法，以保证有效降低传动间隙；位置环设置在PLC控制器中，以实现伺服转台系统的精确定位功能。

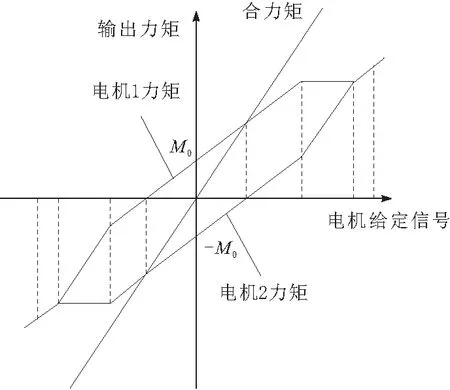
图3 变偏置力矩消隙曲线

3.2 仿真分析

本文所设计的伺服转台的主要参数如表2所示。

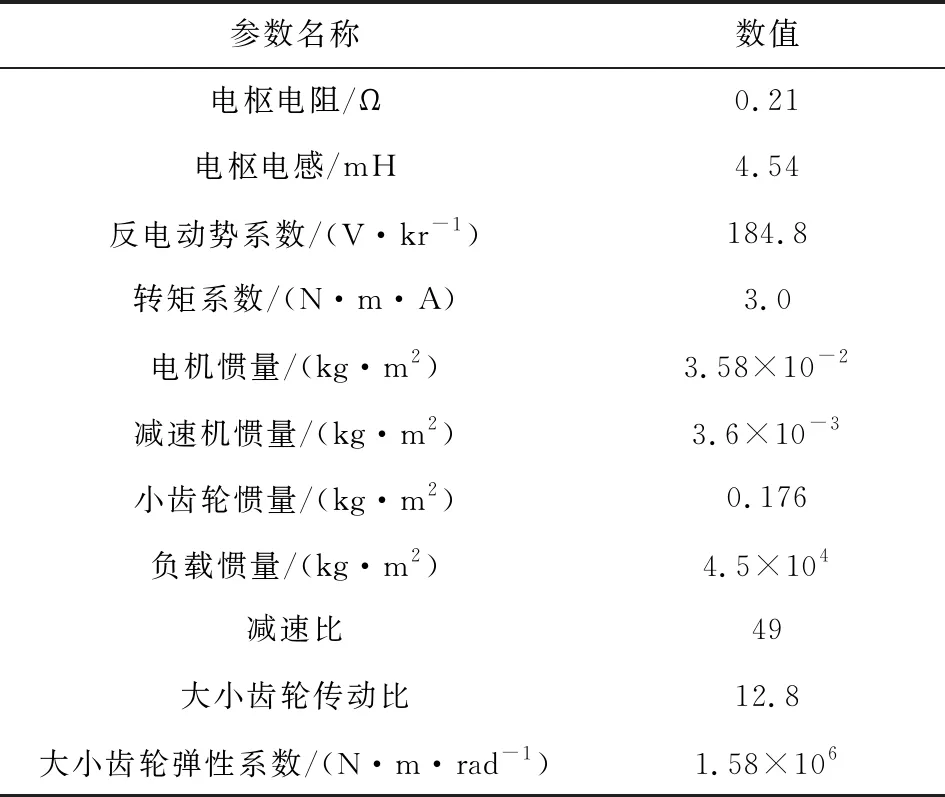
表2 伺服转台主要参数

依据如上参数，在MATLAB/Simulink中，对双电机驱动的伺服转台及控制系统进行仿真建模和分析。为便于表示出仿真模型，将2条支路上的电流环、部分速度环等部分分别封装成2个相同的子系统，整个系统的仿真模型如图4所示。

如图4所示，在位置环中引入前馈控制器，通过调节各环路控制器参数，得到伺服转台系统给定单位阶跃指令下的响应曲线，如图5所示。

图5 系统单位阶跃响应曲线

由图5可知，在给定单位阶跃信号的情况下，所设计的双电机驱动的伺服转台及控制系统，其系统响应的上升时间tr为0.017 s，超调量为0.35%，符合设计预期。

为验证所设计的伺服转台及控制系统的跟踪性能，给定正弦信号指令：y(t)=28.125 sin(0.51t)，并通过调节各环路控制器参数，得到伺服转台系统跟踪误差曲线如图6所示。

图6 给定正弦信号系统跟踪误差曲线

由图6可知，在给定正弦信号的情况下，所设计的双电机驱动的伺服转台及控制系统，其跟踪误差最大达到0.034 4°，符合设计预期。

4 伺服转台系统指向精度分析

影响整个伺服转台系统指向精度的因素，除上述分析的伺服系统最大跟踪误差0.034 4°(2.064′)，还需考虑其他除传动间隙之外的机械结构方面的误差[8]。主要考虑如下几方面：

a.回转支撑加工误差造成的轴系偏差(两面)φ1，约为0.020′。

b.减速机的刚性最大变形量折算到回转支撑上的角误差φ2，约为0.130′。

c.风力、温差、加速度等引起的结构变形，以及日光照射不均匀引起的热变形等因素所造成的总误差φ3，约为0.020′。

d.各类结构件、传感器的安装误差所引起的机械误差φ4，约为1.200′。

综上，整个伺服转台系统总的误差φ为

2.391′≈0.04°<0.05°

由上述分析可知，本文所设计的双电机驱动的伺服转台及控制系统总误差约为0.04°，满足系统跟踪精度指标要求。

5 结束语

本文对某雷达所采用的双电机驱动的精密伺服转台及控制系统进行了详细的设计，并在MATLAB/Simulink中建立整个伺服转台及控制系统的模型，对其进行了仿真试验。仿真系统动态响应结果表明，本文所设计的双电机驱动的精密伺服转台及控制系统对减小传动间隙误差，提高跟踪精度等方面具有积极的作用，满足系统设计指标要求，为后续实际系统研制和调试提供参考。