硅锭电火花线切割对称式张力控制研究

刘 鹏，罗福源，孙凌云

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

硅晶体材料的硬脆特性导致传统加工难以满足大尺寸、高精度、低损耗、绿色环保的切割要求[1-2]，而高速往复电火花线切割因其非接触加工方式正逐渐成为硅晶体的有效加工手段[3]。但是在切割加工过程中，电极丝由于受到诸多外界因素干扰，其张力值始终发生变化，这必然会影响电极丝形位的稳定性[4]，严重影响硅片表面的切割质量与加工的稳定性。因此对电极丝张力的控制已经成为半导体材料电火花加工中的一个关键问题。

为改善电极丝张力波动等问题，国内外学者进行了深入研究和探索。丁成才等[5]对不同电极丝恒张力控制装置进行了对比研究，发现弹簧式的张力恒定效果最明显，磁粉式对张力的恒定起效慢，但具有张力调节方便、快捷的优点；蒋近等[6]使用伺服电机代替重锤施加张力，通过伺服电机的编码器反馈实时位置，调整收放线电机速度，保证切割线张力稳定。张义兵等[7]使用转矩电动机来代替张力锤进行张力调节，运用自适应逆算法设计智能控制器来控制张力；Saha等[8]使用神经网络遗传算法研究电极丝恒张力的控制以及加工参数对TiC 加工时的影响；Yan 等[9]运用基于遗传算法的模糊逻辑控制器控制走丝系统，研究电极丝的恒张力控制。这些学者在控制方法上做出了较为深入的研究，但他们仅仅对一端电极丝张力进行控制，并没有分析走丝结构与控制方式对于加工区域电极丝张力的影响。

1 非对称式单边恒张力控制

1.1 非对称式单边控制策略张力数学模型

在电火花线切割机床放电加工过程中，电极丝的运行状态分为匀速运动状态和换向状态。换向期间机床电火花电源停止放电，伺服电机停止进给运动，因此该阶段电极丝张力状态可以不予考虑。匀速走丝状态是指储丝筒以恒定速度旋转，正常放电加工的状态，电极丝大部分时间处于此状态，此状态的电极丝张力的稳定性及其控制精度对硅片表面切割质量影响重大，根据机床走丝结构建立如图1所示张力模型，建立数学模型时作如下假设：

a.电极丝在放电加工阶段匀速走丝，无加减速，不考虑工作液冲击扰动、放电爆炸力和周围电磁场等因素。

b.电极丝与导轮之间无相对运动，电极丝在导轮处受的摩擦力为轴承的滚动摩擦力。

c.丝与导电块之间接触良好，电极丝在导轮或者导电块处正反转时摩擦系数不变。

正向切割时，放丝端的电极丝经过导电块以若干导轮进入放电加工区域，对硅片进行切割加工，因此在正向切割阶段各段电极丝张力的递推公式可以表示为

Ti+1=Ti+fi

(1)

Ti+1为第i+1段电极丝内部张力值；Ti为第i段电极丝内部张力值；fi为第i段电极丝经过导轮或者导电块所受的摩擦力。

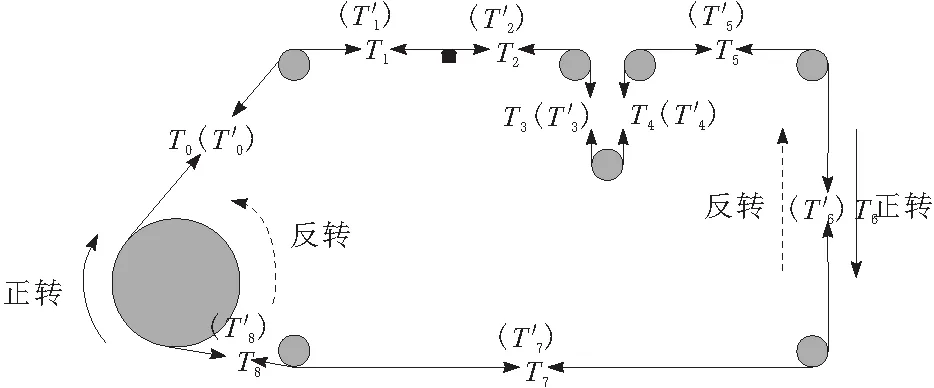
图1 非对称式走丝电极丝受力模型

电极丝受力分析如图2所示。由图2可知，电极丝在导轮以及导电块处所受的摩擦力不同。电极丝与导电块之间存在相对运动，因此导电块处电极丝所受的摩擦力为滑动摩擦力fd。电极丝与导轮以相同的线速度运动，两者之间并不存在相对运动，因此电极丝在导轮处所受的摩擦力为静摩擦力fs，此时电极丝所受的摩擦力可以等效为导轮所受合力对滚动轴承的滚动摩擦力。

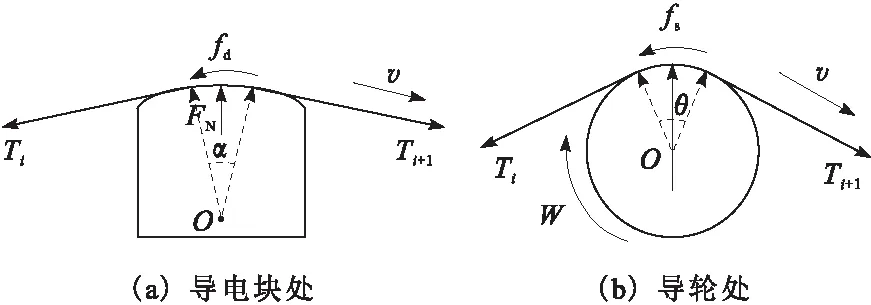
图2 电极丝受力分析示意

根据柔性体摩擦的欧拉公式，可以推导出导电块对电极丝的滑动摩擦力为

fd=(eμ α-1)·Ts=(1-eμ α)·Tl

(2)

μ为导电块与电极丝之间的滑动摩擦系数；α为导电块与电极丝接触时的围包角；Ts为与运动方向相反一端电极丝张力；Tl为与运动方向相同一端电极丝张力。

轴承的摩擦力可以通过轴承的摩擦力矩间接获得，此处影响滚动轴承摩擦力矩的因素有很多，本文中采用一般的计算方法[10]，相关公式可以表示为：

Mf=M0+M1

(3)

(4)

M1=μ1P1dm

(5)

M0为与轴承载荷大小、粘度、润滑、转速等有关的摩擦力矩；M1为与轴承载荷大小、载荷系数有关的摩擦力矩；P1为轴承载荷；μ1为载荷系数；μ0为考虑润滑方法以及轴承结构的系数；v为润滑脂的基油粘度；n为轴承转速；dm为轴承平均直径，取内径外径和的平均值。因此非对称式单边张力控制在正向走丝阶段，放电加工区域的电极丝张力可以表示为

(6)

f1为导电块与电极丝之间的滑动摩擦力；fi为正向走丝时导轮所受的滚动摩擦力。两者计算方法可以表示为：

f1=fd=(eμ α-1)·T1

(7)

(8)

同理，反向走丝阶段加工放电区域的电极丝张力可以表示为

(9)

1.2 张力数学模型分析

图3 非对称式单边张力控制各段电极丝张力条形图

2 对称式双边恒张力控制方案设计

2.1 走丝结构设计

设计图4所示的对称式双边张力方案，在上下丝架分别安装张力传感器与张力执行装置，正向走丝时，下丝架传感器检测收丝端张力值，将采集到的张力值送给运动控制器，控制器通过计算张力的偏差值来控制下丝架伺服电机的运动，从而控制其收丝端的张力值。反向走丝时，上丝架传感器检测收丝端张力，运动控制器通过反馈的上丝架的张力值来控制上丝架伺服电机的运动。

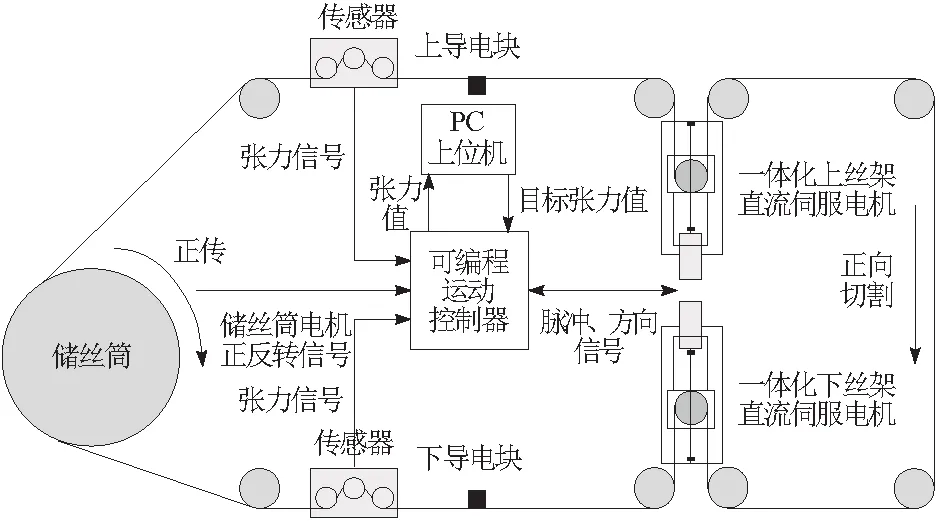
图4 对称式双边张力控制系统原理

2.2 对称式双边控制策略张力数学模型

采用同样的方法构建双边对称式恒张力控制策略中电极丝张力物理模型，如图5所示。

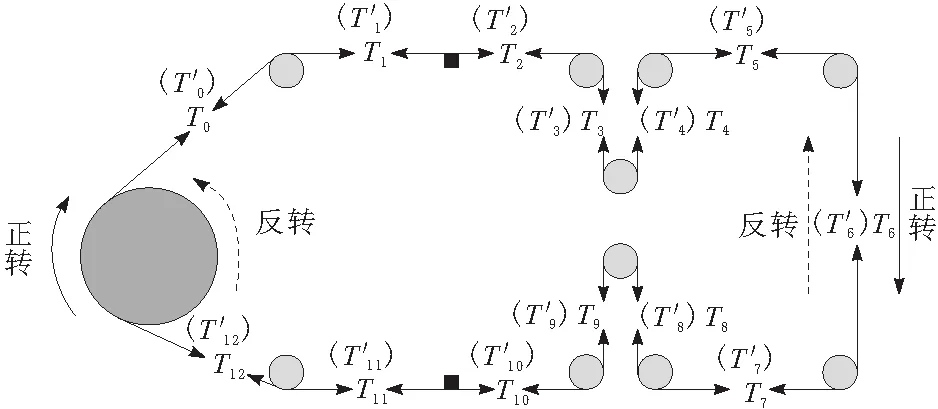
图5 对称式双边走丝机构电极丝张力模型

正向走丝阶段，下丝架电极丝为收丝端，上丝架电极丝为放丝端，各段电极丝张力值的递推公式可以表示为

Ti=Ti+1-fi

(10)

fi为第i段电极丝经过导轮或者导电块所受的摩擦力，计算方式在上一节中已经给出，正向走丝时加工区域的电极丝张力可以表示为

(11)

f10为正向走丝时下丝架电极丝与导电块之间的滑动摩擦力，其计算方法可以表示为

f10=fd=(1-eμ α)·T11

(12)

反向走丝时，上丝架电极丝为收丝端，下丝架电极丝为放丝端，各段电极丝张力值的递推公式可以表示为

(13)

同理，反向走丝时加工区域的电极丝张力与传感器检测处的张力值之间的关系可以表示为

(14)

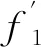
(15)

2.3 对称式双边张力模型分析

通过正反向走丝的各段张力递推公式以及相关参数可以分别求出正反向加工时电极丝的各段张力值，如图6所示。

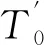
由图7a可以看出，T1处电极丝张力始终保持不变，距离控制点越远电极丝张力差值越大，加工区域电极丝正反向走丝时张力差值高达0.49 N，通过非对称式单边恒张力控制方式，将难以保证加工区域电极丝的张力值均衡性与稳定性。

由图7b可以看出，在对称式双边张力控制方案中，距离加工区域越远的位置处，电极丝张力值因走丝方向改变变化幅度越大，例如收丝端和放丝端电极丝张力值，在正反向走丝时差值为0.55 N。但是加工区域电极丝的张力在正反向切割时具有良好的一致性，仅仅相差0.02 N。对称式双边恒张力控制策略能够使加工区域电极丝张力具有良好一致性，原因在于这种走丝结构的上下丝架导轮数目以及导电块具有良好的对称性。控制结构上的对称性保证了上下丝架电极丝所受摩擦力的对称性。

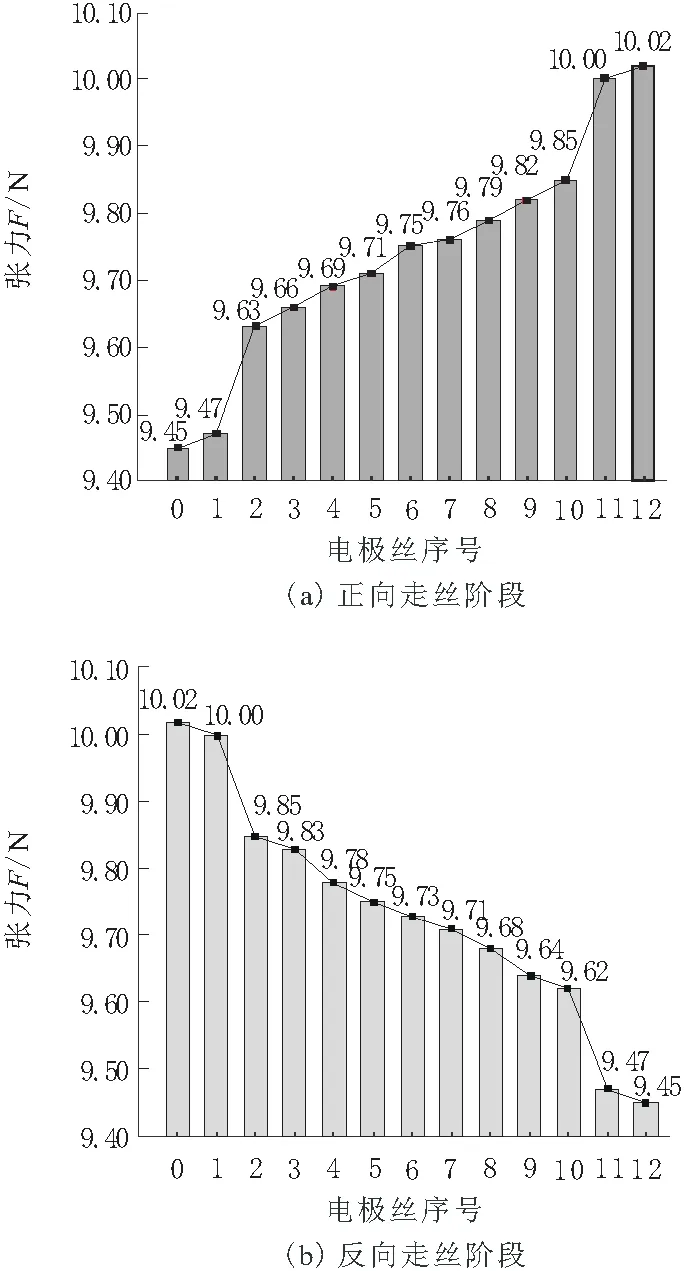
图6 对称式双边恒张力控制各段电极丝张力条形图

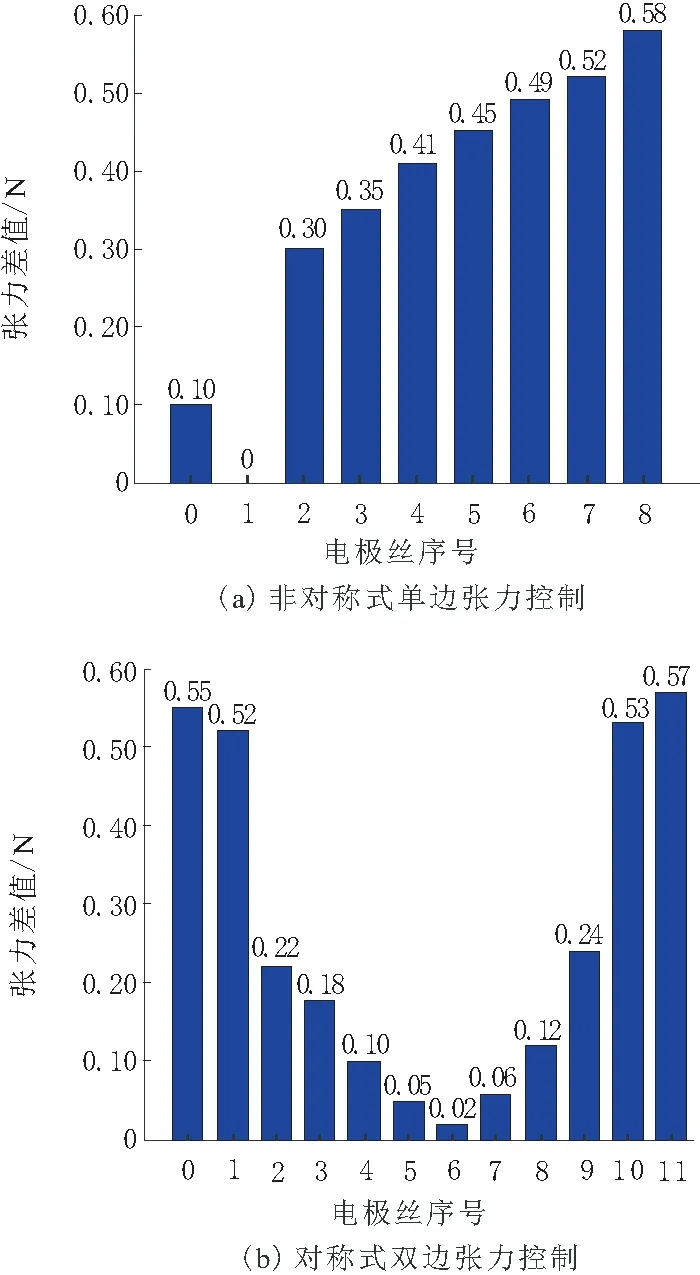
图7 正反向走丝电极丝张力差值条形图

3 对称式双边张力控制系统建模

3.1 分时切换控制方案

本文设计的对称式双边恒张力控制方案存在2套张力执行机构，分别位于上丝架与下丝架，若此时采用2台电机联动协调控制，控制系统将变得异常复杂，可靠性也会大大降低。针对此问题，本文采用“分时切换控制”的控制思想，即在任意时刻只存在1套伺服装置进行控制，整个控制方案的流程如图8所示，其关键点在于切换瞬间，张力控制系统要满足较快的响应特性以及较小的超调量。

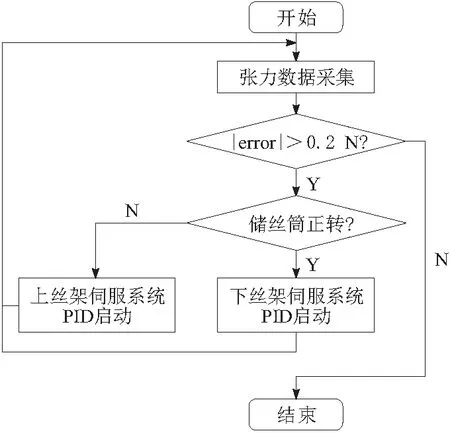
图8 分时切换控制流程

3.2 控制系统模型构建

本文中将电极丝张力控制过程简化成如图9所示。

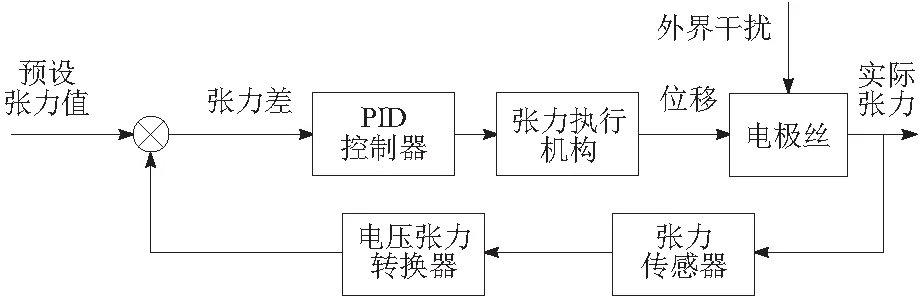
图9 张力控制框图

传感器作为反馈装置，输出与输入成正比例关系，因此可将此部分视作张力值的增益部分，传递函数可以表示为

H1(s)=K1

(16)

电压张力转换器将电压信号线性转化为张力信号，因此可将这一部分也视为输入增益，传递函数为

(17)

执行机构是位移输出，并直接作用于电极丝，电极丝长度的改变对应着张力的变化，其传递函数可以表示为

(18)

张力执行环节由直流伺服电机以及丝杆组成，电机通过联轴器与丝杆相连，丝杆带动张力调节轮上下运动，从而驱动电极丝长度改变，进行张力实时调整，张力执行机构以位移为输出的传递函数为

(19)

传递函数中参数数值及其含义如表1所示。

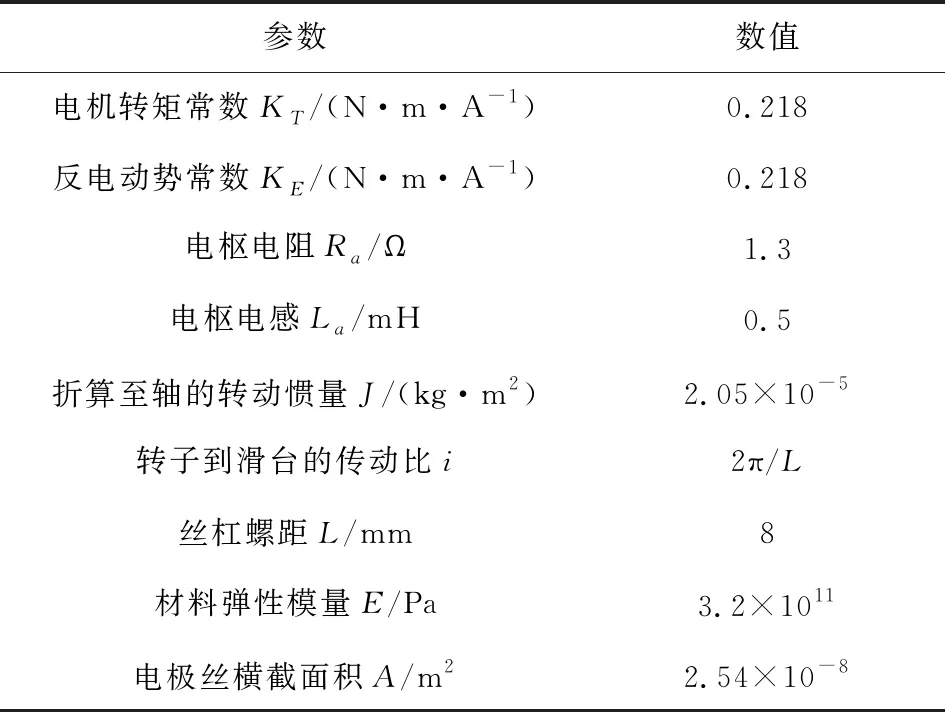
表1 传递函数中的相关参数

为验证PID算法控制效果以及控制系统的稳定性，本小节使用Simulink模块搭建仿真模型。给系统输入一个单位阶跃信号，并不断调节PID的3个参数，当KP=130.8，KI=12.0，KD=2.5时可以得到如图10所示的阶跃响应信号以及误差跟随信号。

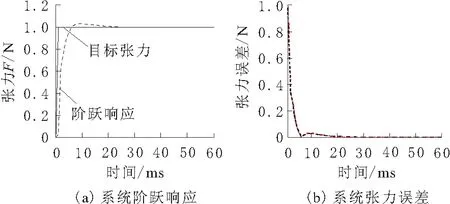
图10 阶跃响应及误差跟随信号

由图10可知，响应信号上升时间约为0.01 s，超调量小于5%。并且系统达到稳定的时间约为0.03 s，稳定时误差接近于0。可知本文设计的恒张力控制系统可以在保证较小超调量基础上实现张力迅速调整，调整时间在0.03 s以内，满足实际需求。

4 实验与分析

恒张力控制试验样机如图11所示，运用此样机可以分别完成3种不同控制策略的张力控制实验。弹簧紧丝器用来完成弹簧式恒张力控制，2套伺服执行机构配合FPGA控制器完成对称式和非对称式恒张力控制。

图11 双边恒张力控制试验样机

实验开始前设定控制系统的目标张力值为10 N，检测加工区域电极丝张力实时波动情况如图12所示。

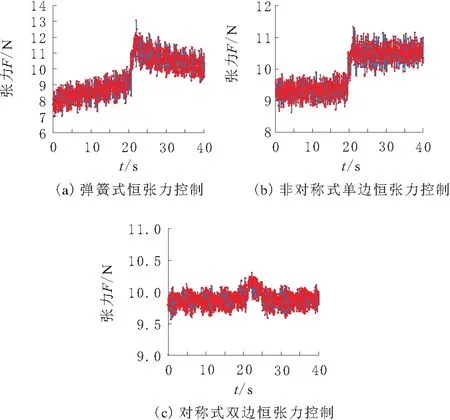
图12 加工区域电极丝实时张力值

由图12a可以看出，在弹簧式恒张力控制方式下，换向阶段有4 N左右的张力波动幅值，正反向切割时张力波动率在20%以上，反向切割时张力随时间呈现递增的趋势，正向切割时张力随时间呈现递减的趋势，难以维持一个稳定的张力值。

由图12b可以看出，在非对称式单边恒张力控制方式下，电极丝张力波动情况得到改善，波动率降低到10%左右。但是存在加工区域张力正反向加工时不一致的现象，反向切割时张力值在9.4 N附近波动，正向切割时张力值在10.5 N附近波动，相差1.1 N。

由图12c可以看出，在对称式双边恒张力控制方式下，加工区域电极丝张力在9.9 N附近波动，正反向走丝时电极丝张力具有很好的一致性，且张力波动率在5%以内，张力波动率仅为非对称式单边恒张力控制方式的50%，换向时冲击在0.5 N以内，满足硅片切割对张力波动的苛刻需求。

5 结束语

针对现有机床电极丝张力波动幅度大、加工区域张力正反向走丝时不一致的问题，设计了双边对称式张力控制方案，并从数学模型的角度指明了此方案较单边非对称式控制方案的优越性。随后，对设计的控制系统进行仿真，仿真结果表明控制系统具有良好的稳定性和响应特性。最后，在实验室环境下设计张力控制对比实验，实验结果表明，本文设计的控制方案可以将加工区域张力波动率控制在5%以内，并且解决了因走丝方向不同导致的加工区域张力不一致的现象，满足硅片切割对于电极丝张力的需求。