基于科创板波动性的实证研究
2021-04-25郭建峰白瑜瑜
郭建峰,白瑜瑜
(1. 西安邮电大学经济与管理学院,陕西 西安710061;2. 英国雷丁大学亨利商学院,雷丁RG6 6AH)
一、 引言
2018 年11 月5 日,习总书记在中国首届上海国际进口博览会开幕式上提出设立科创板并在上海试点注册制。 该板块是独立于现有主板市场的一个新设板块,实现了我国科技型和创新型中小企业融资的重大制度创新。
波动性被认为是最能反映金融市场资产价格变化的基本特征之一,所以适当的波动性已经成为衡量当前金融市场健康运行最直接、最简单的指标。 2019 年7 月22 日,科创板正式挂牌上市。 由于市场还不够成熟,交易数据较少,用传统交易数据建模分析的方法不能够很好地分析和预测科创板的波动性。 根据当前市场的实际交易情况,由于单一模型的结果过于武断,对问题的分析过于片面以及结合实际交易情况,使用R 语言和Winbugs 软件对SV-N 和SV-T 模型进行贝叶斯分析,采用MCMC 方法来拟合科创板市场的波动性。
二、 文献综述
吕红兵和朱奕奕认为我国证券市场参与者应重新审视和构建自身的监管职能,进而形成一种高效且合理的监管,实现政府和市场之间的互动。 黄登仕和王辉认为科创板作为一种新的制度供给对我国经济高质量发展具有重要的作用,但存在缺陷,他们提出了从各个方面完善科创板制度供给的对策。 张群辉通过对双重股权结构背后的机制进行分析,得出:科创板应该在信息披露、股权转让等方面制定相关的规定来保护投资者利益。
姚德权和曹海毅采用派许加权平均法编制我国A 股传媒业振兴指数,通过实证得出该指数能够很好地反映股票价格的波动,具有实际应用价值。 王源昌等采用派式加权法编制云南板块指数,通过实证分析得出该指数反映了云南上市公司股票的整体波动情况,且走势和沪深300 指数走势一致。 一般来说,指数编制的方法有算术平均法、几何平均法和加权平均法。 与前两种方法相比,加权平均法更能真实地反映出市场的整体走势。
杜俊娟通过上证指数的农业股信息,运用MCMC 方法研究随机波动模型对于农业经济的波动性影响。 张静和张旭以招商银行理财产品为研究对象,采用不同的SV 模型研究收益率波动性,结果表明SV-T 模型对于研究收益率波动性有显著的效果。 赵慧琴和刘金山用MCMC 方法研究上海股市的波动性,结果表明:SV-T 模型可以更好地适应上海股市的“尖峰厚尾”特征。
但是,目前关于科创板波动性实证研究的相关文献较少,大多数都是介绍科创板市场以及科创板上市的各种制度、准则等,所以无法在前人的基础上来参考研究。 论文选取从2019 年7 月22 日到9 月30 日首批上市的25 家公司10分钟的高频交易数据科学构造指数,采用基于MCMC 模拟的贝叶斯方法进行实证分析。
三、 模型原理
论文的模型构建将基于以下的理论基础。 研究收益率波动性主要采用两类模型:自回归条件异方差模型(ARCH模型)和随机波动模型(SV 模型)。 Taylor 在1986 年解释和研究金融产品收入序列波动率的自回归行为时提出的随机波动率模型,称为SV 模型。 SV 模型将波动率视为不可观察的随机过程,新的随机变量被添加到SV 模型中,使得长期波动率预测和波动序列稳定性的拟合效果优于传统ARCH 模型。 长期的研究结果表明,相对于ARCH、GARCH 模型,SV模型对于新兴交易市场尤其是刚刚设立的交易市场波动率的预测具有很好的适应性。
考虑到我国科创板市场于2019 年7 月22 日开始正式交易,无论是交易股票数量还是交易额都处于成长阶段,积累的交易数据有限,市场尚未成熟,交易制度尤其是监管制度也在逐步完善,且刚刚上市交易的股票价格波动明显,故论文最终选用SV 模型来研究科创板市场收益率的波动性。
(一)随机波动模型
在讨论随机波动模型时,Taylor 在讨论和解释不同金融资产的预期收益序列的自回归行为时,引入了标准的SV 模型,简称SV-N 模型。 其形式如式(1)所示。
标准SV 模型:

式(1)中,SV 模型的波动率是由均值方程和波动方程组合构成。 其中,SV 模型的波动率是对数形式的波动率。yt表示t时刻的波动率;εt为独立同分布的白噪声干扰,服从正态分布N(0,1);ηt是独立同分布的波动的扰动水平,服从正态分布N(0,τ2)。 在标准SV 模型中误差项ηt与εt都是一个不可能被观测的值,且二者之间不具有任何的相关性。
为了描述金融交易波动数据的“尖峰厚尾”的特征,Kim等将标准SV 模型扩展为一般模型,称为厚尾SV 模型(SVT)。 该模型能够从时间序列中捕获“尖峰厚尾”的特征。 其形式如式(2)所示。
厚尾SV 模型:
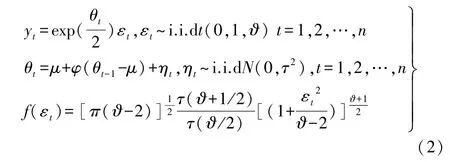
式(2)中前两个模型式子的含义与SV-N 模型一致,第三个式子明确地描述了金融数据“尖峰厚尾”的特征,当4<ϑ<∞时,t分布的峰态系数大于3,ϑ→∞时就为正态分布,ϑ<4时其峰态系数不存在。
(二)随机波动模型估计
SV 模型可以很好地刻画金融交易数据的特征,在金融研究领域应用广泛。 论文基于经典的贝叶斯原理构造SV 模型的后验分布,然后通过Gibbs 抽样方法估计SV 模型的参数和分析其波动性。
1. 贝叶斯推断
贝叶斯推断的基本思想:若θ为一个待估参数或向量,样本为x1,x2,…,xn,以p(x1,x2,…,xn|θ)为样本x1,x2,…,xn对θ的条件密度,称为似然密度函数,h(θ|x1,x2,…,xn)表示θ对x1,x2,…,xn的条件似然密度,即后验分布密度,贝叶斯公式如下:
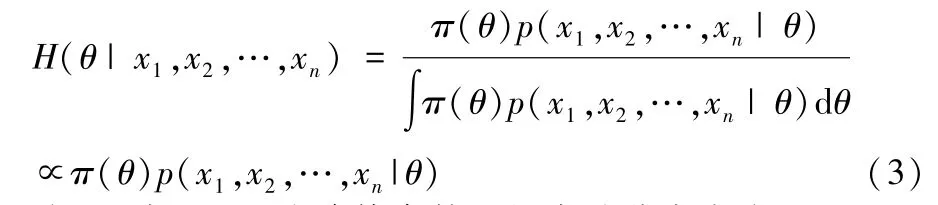
式(3)中,π(θ)为待估参数θ的先验分布密度。 即通过h(θ|x1,x2,…,xn)推断出待估参数θ,也可以对待估参数θ进行估计和检验。
2. MCMC 模拟
MCMC 的原理:给定随机数学过程{Xt},假设每个贝叶斯Xt的值为状态空间⊃中任意一个贝叶斯值。 若我们给定一个Xt值,Xh值不随着Xs值的变化而变化,s<t,这样就把该随机过程{Xt}称为马尔可夫过程。 即如果随机数学过程{Xt}是马尔可夫过程,则该随机数学过程的条件分布函数必须满足以下式子:

如果{Xt}过程是离散的随机过程,则式(4)可以变成

设A为状态空间⊃中的一个子集,则转移概率函数Pt(θ,h,A)=P(Xh∈A|Xt=θ)(h>t)为马尔可夫过程的一个转移概率函数。 如果该过程中转移概率只是依赖于h-t而不依赖于t,那么称该马尔可夫过程有一个稳定的转移概率分布。
3. Gibbs 抽样
Gibbs 抽样原理:假设一个n维随机变量向量θ=(θ1,θ2,…,θn),不知道其联合分布,只知道每个随机变量θi在给定其他随机变量的条件下满足条件分布θ=(θi|θ1,θ2,…,θn),这时就可以直接使用Gibbs 抽样。 假设给定一组初始值θ0=(θ1.0,θ2.0,…,θn.0),则这个抽样过程可以表示为:
从分布p(θ1|θ2.0,…,θn.0)中抽取θ1.1;
从分布p(θ2|θ1.0,θ3.0,…,θn.0)中抽取θ2.1;
……
从分布p(θn|θ1.0,θ3.0,…,θn-1.0)中抽取θn.1,这样就完成了一次Gibbs 迭代,得到了θ1=(θ1.1,θ2.1,…,θn.1)。
重复上述步骤,就可以得到θ1,θ2,…,θn,去掉前m次得到剩下的θm+1,θm+2,…,θn,当m足够大时,就可以把θm+1,θm+2,…,θn看成是分布p(θ|X),这样就可以根据此序列来做统计推断,即
四、 实证分析
论文选用科创板开市以来第一批挂牌上市的科创板企业,2019 年7 月22 日开盘到9 月30 日期间每隔10 分钟的股票收盘价作为基础数据。 用加权平均法构建科创板指数(简称为“科指”),采用加权平均法编制指数,简单易懂,便于计算,同时,这也是很多指数包括上证指数构建的方法。 根据各个上市企业在科创板市值所占的比重来构建该科创板指数,具体公式为:

使用SV 模型建模时,通常使用对数收益率:yt=100×(lnpt-lnpt-1),pt表示在t时刻科创板指数的收盘价,yt表示t时刻股票的对数收益率。 论文统计和研究所用数据均来源于Wind 数据库,所用的软件为WinBUGS14。
(一)标准SV 模型建模
在标准SV 模型中,每个先验参数都是独立的。 参考古典物理学者Kim 对标准模型中各参数的先验分布假设,对各参数的先验分布分别做如下假设:
设φ=2×φ∗-1,其中假设先验参数φ∗服从分布Beta 分布φ(φ(1),φ(2)),于是先验参数φ的先验分布表示为
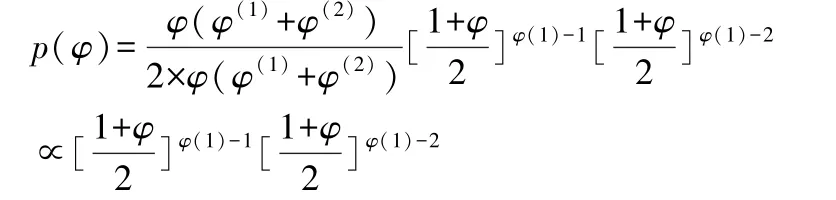
其中,超参数φ(1)的初始值为20,φ(2)的初始值为1.5。参数μ的先验分布当且仅当服从于正态分布N(μ∗,σ2∗),其中超参数μ∗取0,σ2∗取100。 参数τ2的先验分布服从于逆分布取为Gamma 分布IG(σr和sσ),其中超参数σr和Sσ分别取为2.5,0.025。
SV-T 模型中多了参数ω,先验分布为ω~(8)I(4,40)。
(二)厚尾SV 模型建模
与标准SV 模型类似,在Gibbs 采样过程中获取初始值μ=0,φ=0.95,τ=0.02,ω=-0.6。 为了确保其参数的收敛性,对每个参数进行10000 次迭代并退火,舍弃前500 次迭代后各参数达到收敛状态,通过Gibbs 抽样,得到每个参数的估计值。
表1 为SV-T 模型各参数的均值、标准差、MC 误差、2.5%分位数和97.5%分位数的贝叶斯值。 据Gibbs 抽样,获得每个参数的估计值:

表1 SV-T 模型中科指10min 数据的参数估计值
(1)在SV-T 模型中科指10min 数据的自由度参数ω的值为7.204。
(2)在SV-T 模型中科指10min 数据的波动水平参数μ为-0.6563,波动持续性参数φ为0.8591,参数τ的贝叶斯参数估计值为100.4。
和SV-N 模型不同的地方是,SV-T 模型中加入了自由度。 从图1 可以明显地得出:SV-T 模型中10min 数据参数ω的拟合效果更形象。 采用MCMC 方法进行模拟估计的参数值是准确的。

图1 科指10min 数据SV-T 后验分布密度函数仿真图
五、 结论
论文通过对收盘价进行指数构造,以10min 高频数据作为样本,采用SV-N 和SV-T 模型来研究科创板的波动性。通过贝叶斯原理,构造基于Gibbs 抽样方法的MCMC 模拟仿真过程,并对两个模型进行实证分析,结果均表明:科创板指数收益率波动较大且持续时间较长,且SV-T 模型的拟合效果明显优于SV-N 模型。
通过对收益率波动性的综合分析,可以很好地评估和预测金融风险。 科创板是新设立的一个板块,对于投资者来说,应当充分了解和掌握各种交易制度,加强风险识别能力,学习相关专业知识,进而进行准确、合理的投资;对于监管者来说,科创板制度的创新导致价格资产波动明显,给监管者带来了一定的挑战,另外科创板收益率波动性明显,这就要求加强信息披露和投资者与上市公司之间的沟通;对于机构投资者来说,科创板“尖峰厚尾”的特性吸引了更多的投资者参与进来,而这种虹吸效应,使得其他市场资金回流到科创板市场,引发了各个市场对机构投资者的争夺,造成更大的波动性和流动性;对于研究人员来说,目前上市公司不多,股票数量不够,数据交易时间较短,这都将对研究科创板收益率波动性产生影响。 随着科创板市场的不断交易,交易数据和上市公司将不断增加,这会使得对科创板市场波动性的研究具有更坚实的基础。
