问题链:让学生在探究中体验数学美
2021-04-22陈明叶玲菊张红
陈明 叶玲菊 张红
摘要:数学美需通过具有探究性的数学学习活动来体验。数学问题链教学强调利用主干问题及其关系驱动学生的数学探究,体现数学思维的脉络,因此,可以成为引导学生体验数学美的重要方式。《平行四边形角平分线问题》一课,以问题链为载体,让学生:发现关联,体验和谐美;繁中抽简,体验统一美;不断拓展,体验生长美。
关键词:问题链教学;数学探究;数学美;《平行四边形角平分线问题》
数学是美的,但“与一般的美感不同,数学美感主要是指因为理解、认识或发现(或意识到、领悟到)某种数学内在实质、数学关系结构或数学思想方法等而产生的愉悦感、满足感、兴奋感、新奇感等”;“深层的数学美感主要是在潜心思考后所获得的灵感与顿悟中感受的,也是在超越自然后所获的自由与统一中感受的”。因此,数学美需通过具有探究性的数学学习活动来体验——可以说是,像数学家一样,通过“火热的思考”来体验“冰冷的美丽”。这是数学学习(研究)中比较高的境界。
数学问题链教学强调利用主干问题及其关系驱动学生的数学探究,体现数学思维的脉络,因此,可以成为引导学生经历数学发生、发展的过程,发现数学的本质、结构,领悟数学的思想、精神,从而体验数学美的重要方式。教学《平行四边形角平分线问题》一课时,我们便着力思考如何通过问题链让学生在探究中体验数学美。
这节课是教学完平行四边形的相关知识后的一节专题复习课。其目的是,一方面让学生综合应用平行四边形的性质,另一方面讓学生像数学家一样思考、研究数学问题。其基本思路是,在作出平行四边形一条角平分线的基础上,发现图形中存在的等量关系、特殊对象等,研究图形变化中的不变性(繁中抽简);进而在增加角平分线数量的基础上,研究相关问题,体验数学思维的生长性。
一、发现关联,体验和谐美
结构化是数学的一个典型特征,数学对象之间存在着各种各样的关联。而数学对象之间关联的发现过程能让人体验到一种和谐美。在几何中,这种美既体现在几何对象的位置关系上,又体现在几何对象的数量关系上。因此在教学中,教师要有意识地创造机会,让学生经历几何关系的发现过程,体验数学对象之间的和谐美。
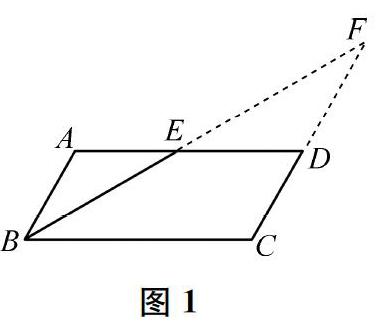
问题1如图1,BE是平行四边形ABCD中∠ABC的平分线。请仔细观察,你能由此发现哪些几何关系?
问题1是这节课的起点性问题,难度较低,可以引出课题和后续问题(平行四边形角平分线的有关问题)。在教学中,教师直接呈现问题1,让学生自主探索。学生由于比较熟悉几何图形中的边、角等基本元素,几何对象的相等、比例等数量关系,平行、垂直等位置关系,以及特殊的几何对象等几何研究的基本角度,因此能够自然地从上述角度出发寻找几何关系。比如,从角的相等关系角度发现∠ABE=∠EBC=∠AEB=∠FED=∠DFE,由此转向线段相等关系的角度,发现AB=AE、FD=ED、FC=BC,进而转向特殊几何对象的角度,发现△ABE、△DFE、△CFB均为等腰三角形。这样,从平行四边形的一条角平分线出发,发现丰富的角、边的相等关系以及特殊的几何对象,让学生体会到数学对象之间的和谐美。而且,这些关系都是学生根据已知条件自己找出来的,因此,美的体验也更为强烈。
二、繁中抽简,体验统一美
米山国蔵认为,数学中充满着统一建设的精神,教师应将这种精神教给学生。事实上,统一性既是数学发展中的一种精神追求,又为数学发展提供了一种方法论。欧几里得的《几何原本》和布尔巴基学派的公理化运动即是这一方面的典型例证。具体地,统一性旨在寻求纷繁多样的数学对象和数学问题背后数学本质和数学思想上的一致性或相似性,明晰数学知识的内在逻辑,因此,能让人感受到发现变化中的不变性(繁中抽简)后的统一美。在教学中,教师要有意识地渗透一般化思想,引导学生发现变化中的不变性。
问题2是否从平行四边形所有内角的平分线出发都能得到上述结论?
问题3是否从所有平行四边形出发都能产生上述结论?
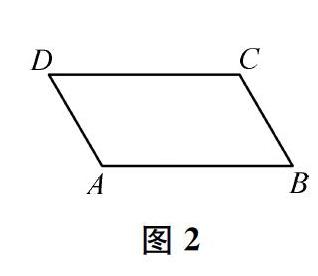
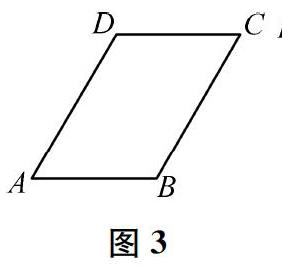
问题1给定了一个特殊平行四边形的一个特殊角。因此,站在一般化的角度,学生容易提出问题2和问题3。具体地,有学生由图1自然会想到∠ABC与∠BAD(或∠BCD)是有差异的,甚至怀疑∠ABC与∠CDA也是有差异的,于是提出问题2;也有学生由图1自然会想到平行四边形ABCD的位置(形状)比较特殊,还能画出其他位置(形状)的平行四边形(如图2—图4),于是提出问题3。
在教学中,教师没有直接让学生一个个地探究问题2和问题3中的各种情况,而是组织学生先思考问题2中的四个角能否分类、归并,问题3中的四种位置(形状)具有怎样的内在关系,并通过“画图—旋转(翻折)—观察—分析”的方法来解决。具体地,针对问题2,要求学生画出角平分线,直观感受角平分线与边交点的位置;进而以两条对角线的交点为中心,将平行四边形顺(逆)时针旋转180°,发现∠ABC与∠CDA重合,∠BAD与∠DCB重合;因此,只需要再讨论是否从∠BAD的平分线出发也能得到上述结论。针对问题3,要求学生先在纸上画出图1—图4所示的平行四边形,然后从纸的反面看图2,发现与图1一样;以两条对角线的交点为中心,将图3顺时针旋转90°,发现与图2一样;以两条对角线的交点为中心,将图4逆时针旋转90°,发现与图1一样;因此,只需要研究是否从图1所示的平行四边形出发能够得到上述结论。基于此,学生不难发现变化中的不变性。
问题4图1中点E的位置一定在边AD上吗?为什么?
聚焦角平分线与边交点的位置,学生还能提出一般化问题,即问题4。针对这个问题,学生借助问题1中线段的等量关系,利用逻辑推理,反向画出交点在边AD上、与顶点D重合、在边AD延长线上等三种情况的平行四边形。同时,将其与问题3联系起来,使问题3中的四种位置(形状)与问题1中的基本图形建立起另一重关联,从而更加强化对统一美的体验。
三、不断拓展,体验生长美
数学文化观认为,数学是人类的一项创造性活动,本质上不是先验的、固化的,而是经验的、生长的。在教学中,教师要不断地拓展内容(增加对象),深化认识(综合思考),让学生体会数学的生长美。
问题5刚才的研究聚焦于平行四边形的一條角平分线所引发的问题,如果在图1中增加角平分线的数量,又能引发哪些问题,发现什么几何关系呢?
问题5是在问题1基础上拓展内容(增加角平分线的条件)提出的更具复杂性和周延性的问题。针对问题5,学生能够画出图5,进而发现更多的几何关系。比如,AE∥CH,BG∥DF,AE⊥BG,AE⊥DF,CH⊥BG,CH⊥DF(平行四边形对角的平分线相互平行,邻角的平分线相互垂直);四边形ADEF、BCGH为菱形,四边形IJKM是长方形等。此外,图中还有很多等腰三角形、直角三角形和平行四边形。探索这个问题,发现这些结论,是一种美妙的“生长”体验。
问题6平行四边形两个内角的平分线相交时,交点在什么位置?
聚焦两条角平分线交点的位置,学生还能提出一般化问题,即问题6。针对这个问题,类比迁移问题4的探究经验,学生很快感觉到,虽然图5中两条角平分线的交点I、J、K、M都在平行四边形内部,但它们也可能在平行四边形边上或外部;类比迁移问题2和问题3的探究经验,学生能够认识到,考虑到对称性,只需要研究图5中点K的位置。具体地,当DE+CG>CD,即2AD>CD时,点K在平行四边形ABCD内部;当DE+CG=CD,即2AD=CD时,点K在边CD上,且是边CD的中点;当DE+CG 问题7如图6,四边形ABCD是平行四边形,P是边CD上一点,且AP和BP分别平分∠DAB和∠CBA,如果AD=5 cm,AP=8 cm,求△APB的周长。 聚焦问题6中两条角平分线交点的特殊位置,即在平行四边形边上的情况,学生可以根据问题5中得到的几何关系,编制出诸如问题7的习题(并解决)。这也是一种体验数学生长美的方式。 总之,本节课以问题链为载体,引导(驱动)学生深入探究,不断发现几何关系,获得数学结论,从中感受数学的思想和精神,充分体验数学美。 *本文系浙江省教研项目“基于问题链的初中数学课堂教学探索”(编号:G2019156)、全国教育科学规划课题教育部重点课题“指向深度理解的‘问题链教学研究”(编号:DHA200318)的阶段性研究成果。 参考文献: [1] 陈焕斌,张雄.略论数学美的本质属性[J].数学教育学报,2008(5). [2] 王钦敏.感受数学美的两个重要途径[J].数学教育学报,2014(2). [3] 唐恒钧,张维忠,陈碧芬.基于深度理解的问题链教学[J].教育发展研究,2020(4). [4] 米山国蔵.数学的精神、思想和方法[M].毛正中,吴素华,译.成都:四川教育出版社,1986.热点透视
