模态逻辑的集合论语义与互模拟不变性

史璟

本文首先介绍模态逻辑的集合论语义，我们在集合传递闭包上解释模态语言。第二部分定义从模态语言到集合论语言的翻译，引入集合传递闭包之间的互模拟的概念。第三部分讨论集合论语言与一阶关系语言之间的一些联系，这是第四部分证明刻画定理的基础。第四部分，将证明集合论语义下的刻画定理，即一个一阶集合论公式等价于某个模态公式的集合论翻译当且仅当它在集合互模拟关系下不变。也就是，模态语言是一阶集合论语言的集合互模拟不变片段，它是对van Benthem 刻画定理的推广。

1 模态逻辑的集合论语义

巴威斯（J.Barwsie）和莫斯（L.Moss）在著作《恶性循环——非良基现象的数学》中引入了模态语言的集合论语义。（[2]）这种语义在集合上解释模态公式。令ML(◇,Φ)是基本模态语言，其中Φ 可数命题变元集合，◇是一个一元模态词。模态公式按照如下规则定义：

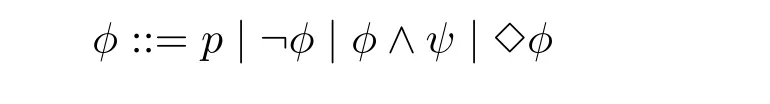
公式φ 在集合a 上是真的（记号：a|=φ）递归定义如下：

(1) a|=p ⇐⇒p ∈a；

(2) a|=¬φ ⇐⇒a/|=φ；

(3) a|=φ∧ψ ⇐⇒a|=φ 且a|=ψ；

(4) a|=◇φ ⇐⇒存在集合b ∈a 使得b|=φ。一个命题变元p 在a 上真定义为p 属于a。因此，集合a 中含有的命题变元不是集合也不是类，我们把这样的元素称为本元，本文使用的本元仅指命题变元；其次，公式◇φ 在集合a 上是真的，定义为存在a 中是集合的元素b 满足φ。我们仅仅在集合上计算公式的真值，而在本元或命题变元上不计算公式的真值。

另一个重要问题是，如上递归定义中使用的集合包括非良基集合。在经典集合论ZF 中有一条公理称为正则公理或良基公理，它是说每个非空集合都有属于关系的极小元。因此不存在无穷下降的属于关系链，不存在属于自身的集合x ∈x，也不存在循环x ∈y1∈...∈yn∈x。非良基集合允许无穷下降的属于关系链，因此允许属于自身的集合，也允许循环。阿克采尔（P.Aczel）在《非良基集合》这部著作中研究了非良基集合，提出了反基础公理AFA。（[1]）非良基集合论ZFA，是把ZF 中的基础公理去掉后再加上反基础公理AFA 得到的。（[6]）

阿克采尔的基本思想是利用集合与图的关系，一个集合可以按照逆属于关系展开为一个图，而一个图通过装饰函数可以转化为一个集合。一个图(G,R)是由结点集G 和结点之间的二元边关系R 组成的，如果Rwu，那么称u 是w 的子结点。一个装饰d 是一个函数，对每个结点w 指派集合d(w)使得：如果Rwu，那么d(u)∈d(w)。在经典集合论ZF 中，Mostowski 坍塌定理说明，每个良基图都有惟一的装饰。每个良基图都对应于由它的所有结点的装饰组成的集合。但是，如果考虑非良基图，比如w 是自身的后继结点，那么d(w) ∈d(w)，这样就存在属于自身的集合。因此，阿克采尔将Mostowski 坍塌定理推广为：每个图都有惟一装饰。由此引入非良基集合。

在模态逻辑中，一个框架F=(W,R)就是一个图。如果框架中有循环结点，比如自返点、对称点等等，那么这个图是非良基图，所对应的集合是非良基集。由于模态公式在框架基础上进行解释，所以，在集合上解释模态语言，就必须引入非良基集合，以便处理循环图。比如模态公式p→◇p 在任何属于自身的集合a上是真的。这样，把集合之间的属于关系看作可及关系，一个集合就可以看作模态语言所谈论的关系结构。反之，给定一个关系结构，也可以通过装饰函数把它与一个集合联系起来。

一般地，对任意非空集合a，它的传递闭包TC(a)定义为∩{b : a ⊆b 并且b 是传递的}，即包含集合a 的最小传递集合。TC(a)中可以含有本元。对每个集合a，令support(a)= TC(a) ∩Φ（Φ 是命题变元集）。集合support(a) 是与集合a 相关的本元的集合。如果support(a)= ∅，那么称集合a 为纯集合。纯集合是不含本元的集合。经典集合论的论域中的集合都是纯集合。一般地，定义论域Vafa[Φ]= {a : a 是集合并且support(a)⊆Φ}。Vafa[Φ]是集合类，它不含本元。此外，把Vafa[∅]写成Vafa，它是由所有纯集合组成的类。

任给非空集合a，a |= ◇◇p 当且仅当存在集合b 和c 使得c ∈b ∈a 并且p ∈c。这里集合b 属于a，但是c 不一定属于a。为保证a 中所有集合中的集合都在a 中，我们递归定义{a}的集合传递闭包STC({a})如下：

• T0=a；

• Tn+1=Tn∪{b:b ∈c ∈Tn并且b 是集合}。

那么定义STC({a})=∪Tn:n ≥0。显然a ∈STC({a})。下面我们在集合传递闭包上解释模态公式。

定义1.任给非空集合a，如下递归定义模态公式φ 在集合传递闭包STC({a})中一个集合b 上真（记号：STC({a}),b|=φ）：

(1) STC({a}),b|=p ⇐⇒p ∈b；

(2) STC({a}),b|=¬φ ⇐⇒STC({a}),b/|=φ；

(3) STC({a}),b|=φ∧ψ ⇐⇒STC({a}),b|=φ 且STC({a}),b|=ψ；

(4) STC({a}),b|=◇φ ⇐⇒存在c ∈STC({a})使c ∈b 且STC({a}),c|=φ。

显然集合传递闭包的作用相当于关系语义学下模型的作用。在集合传递闭包上解释模态语言，不同于在集合上解释模态语言，关键是每次我们从集合中取出的集合都属于集合传递闭包。在后面我们以定义1 提供的模态逻辑语义为基础。

2 集合翻译与互模拟

在这一部分我们引入从模态语言到集合论语言的翻译。在集合论语义下，集合上的逆属于关系恰好可以看作可及关系，而集合本身可以看作状态。因此，很自然也可以把所有模态公式翻译为集合论公式。所使用的集合论语言含如下初始符号：

(1) 集合变元：x0,x1,...（使用x、y、z 等表示）；

(2) 本元符号：p0,p1,...（使用p、q、r 等等表示本元）；

(3) 二元属于关系符号：∈；

(4) 逻辑符号：∀、∃（量词），¬、∧、∨、→（命题联结词）。该集合论语言的公式是由如下规则形成的：

其中p 是本元，本元的集合就是基本模态语言ML(Φ,◇)的命题变元集合Φ。其它联结词和量词可以定义出来。

定义2.定义从基本模态语言到集合论语言的标准集合论翻译π(φ,x)：

(1) 对每个p ∈Φ，π(p,x)=p ∈x

(2) π(¬φ,x)=¬π(φ,x)

(3) π(φ∧ψ,x)=π(φ,x)∧π(ψ,x)(4) π(◇φ,x)=∃y(y ∈x∧π(φ,y))

这里的变元x 和y 都是集合变元；把命题变元直接翻译为集合的本元。同样，对于公式□φ，有如下翻译：π(□φ,x)=∀y(y ∈x→π(φ,y))。在翻译过程中，如果遇到重叠的模态词，由于不同的量词约束不同的变元，可以交替使用变元x 和y。因此，可以把所有模态公式翻译到所定义的集合论语言的两变元片断，即只使用两个变元的集合论语言片段。

例3.模态公式◇◇◇p 的集合论翻译如下：

定理4.对任意集合a ∈Vafa[Φ]和模态公式φ，对每个b ∈STC({a})，如下成立：

证明.对φ 的构造归纳证明。只证明φ:=◇ψ 的情况。显然：

根据上面定义的标准翻译，一个很自然的问题是：是否所有集合论公式都是某个模态公式的集合论翻译？答案是否定的。为证明这一点，首先定义集合传递闭包上的互模拟关系，并且证明所有模态公式在这个互模拟概念下不变。

定义5.任给两个非空集合a 和b，一个非空关系Z ⊆STC({a})×STC({b})称为这两个集合传递闭包之间的互模拟关系，如果它满足如下条件：如果cZd，那么

(1) c ∩Φ=d ∩Φ。

(2) 如果集合s ∈c，那么存在集合t ∈d 使得sZt。

(3) 如果集合t ∈d，那么存在集合s ∈c 使得sZt。

如下图所示：

这里第一个条件意思是c 和d 含有相同的命题变元，因此在集合传递闭包中，它们满足相同的命题变元。第二个条件和第三个条件分别相当于基本模态逻辑中互模拟关系定义（[5]）中的前进条件和后退条件。

命题6.令Z ⊆STC({a})×STC({b})是互模拟关系使得cZd。那么对任意模态公式φ，STC({a}),c|=φ 当且仅当STC({b}),d|=φ。

证明.对φ 的构造归纳证明。只证φ:=◇ψ 的情况。首先假设STC({a}),c|=◇ψ。那么存在s ∈c 使STC({a}),s |= ψ。因此存在t ∈d 使sZt。由归纳假设得STC({b}),d|=ψ。所以STC({b}),d|=◇ψ。反之类似证明。

在关系语义学中，并非每个一阶公式都等值于某个模态公式的标准一阶翻译，一阶公式Rxx 就不等值于任何模态公式的标准一阶翻译（[5]）。那么，在上面给出的集合论翻译下，利用命题6 的互模拟不变结果可证如下命题。

命题7.存在一个集合论公式x ∈x，它不是任何模态公式的集合论翻译。

证明.若不然，假设x ∈x=π(φ,x)。考虑自然数上的属于关系(ω,∈)。再考虑满足方程x={x}的集合Ω，令Z={(n,Ω):n ∈ω}是这两个集合之间的互模拟关系使得每个自然数n 与集合Ω 互模拟。注意，STC({ω})=ω ∪{ω}=ω+1，并且STC({Ω})=Ω ∪{Ω}。由于Ω= {Ω}，STC({Ω})=Ω ∪Ω=Ω= {Ω}。如下图所示：

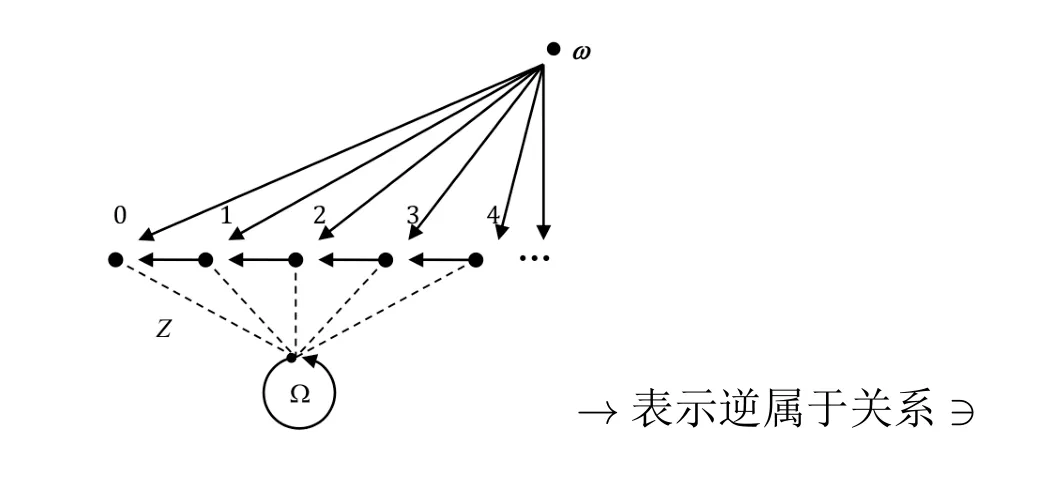
因为STC({Ω}) |= x ∈x[Ω]，所以STC({Ω}) |= π(φ,x)[Ω]。那么根据定理4，STC({Ω}),Ω|=φ。因为每个自然数n 与Ω 互模拟，根据命题6，STC({ω}),n|=φ。再根据定理4，STC({ω}),n |= π(φ,x)，所以STC({ω}),n |= x ∈x，但是n/∈n，矛盾。

由于并非所有集合论公式都等价于某个模态公式的标准翻译，那么一阶集合论语言在集合传递闭包之间互模拟下不变的片段是否等价于模态公式的集合翻译呢？在第四部分证明该问题的答案是肯定的。下面首先给出一些关于集合论语言和一阶语言之间的关系的结论。

3 集合论语言与一阶关系语言

首先我们从模态语言在集合传递闭包上的解释可以看出，在一个集合传递闭包STC({a}) 中元素之间的属于关系相当于关系语义学下可能世界之间的可及关系。因此，我们可以使用任意二元关系R 表示集合上的属于关系∈。如下定义集合传递闭包STC({a})上的关系R：

在对应的一阶关系语言中，对于每一个命题变元p，含有一元谓词符号P，二元关系符号R。对任何模态公式φ，定义它的标准翻译Tr(φ,x)如下：

(1) 对每个p ∈Φ，Tr(p,x)=Px

(2) Tr(¬φ,x)=¬Tr(φ,x)

(3) Tr(φ∧ψ,x)=Tr(φ,x)∧Tr(ψ,x)

(4) Tr(◇φ,x)=∃y(Rxy∧Tr(φ,y))

同样在集合传递闭包下也可以解释上面的公式：任给集合传递闭包STC({a})，令σ 是对变元的指派，一元谓词解释P 为STC({a})中含有相应的命题变元p 的子集，二元关系符号R 解释为集合之间的属于关系。然后如下解释一阶关系语言的公式：

(1) STC({a}),σ |=Px ⇐⇒p ∈σ(x)；

(2) 命题联结词的解释与一阶逻辑相同；

(3) STC({a}),σ |=∃xα ⇐⇒存在b ∈STC({a})使得STC({a}),σ[b→x]|=∃xα这里指派σ[b→x]表示把集合b 指派给变元x。下面我们表明集合论翻译和一阶翻译在集合传递闭包的语义下是等价的。

定义8.如下定义从集合论语言到一阶关系语言的翻译(·)∗：

显然这里定义的翻译(·)∗是一个双射。根据定义，下面这个命题表明在集合传递闭包的语义解释下，集合翻译和一阶标准翻译是等价的。

命题9.对任何模态公式φ，集合传递闭包STC({a})和其中元素b，如下成立：

为了证明刻画定理，我们还要引入另一些定义结论。首先引入超滤扩充的概念。任给集合传递闭包STC({a})和其中的元素b，前面定义了关系R，这里定义R[b]={c:c ∈b 并且c 是集合}。任给一个集合S，令℘(S)表示S 的一个幂集，也就是S 的所有子集的集合。如下定义函数mR:℘(STC({a}))→℘(STC({a}))使得：

令lR(X)=STC({a})mR(STC({a}))。

任给集合S，一个子集族F ⊆℘(S)称为S 上的超滤子，如果它满足以下条件：

(1) S ∈F；

(2) 如果X,Y ∈F，那么X ∩Y ∈F；

(3) 如果X ∈F 并且X ⊆Y，那么Y ∈F；

(4) 对任何X ∈℘(S)，X ∈F 当且仅当SX/∈F。

任给元素x ∈S，由x 生成的超滤子U(x)={X ⊆S :x ∈X}，即所有含x 的自己组成的集合族。在超滤扩充集合中，所有元素都是超滤子，而这些超滤子之间的关系R#是二元关系，而不是属于关系。

定义10.任给集合传递闭包STC({a})，其超滤扩充集合为二元组ueSTC({a})=(Uf(STC({a})),R#)：

(1) Uf(STC({a}))是STC({a})上所有超滤子的集合；

(2) 任给两个超滤子u 和v，定义R#uv 当且仅当X ∈v 蕴涵mR(X)∈u。

根据前面的论述，显然我们可以在任何集合传递闭包上定义等价的模型。任给集合传递闭包STC({a})，定义模型M=(STC({a}),R,V)如下：R 关系即定义(@)；对任何命题变元p，集合b ∈V(p)当且仅当p ∈b。于是很容易得到以下结论。

命题11.任给集合传递闭包STC({a})，令M 是由STC({a})诱导的模型。那么对所有模态公式φ 和集合b ∈STC({a})，STC({a}),b|=φ 当且仅当M,b|=φ。

命题11 建立了模态语言的关系语义学与集合传递闭包语义学之间的联系，这一联系对于证明刻画定理起到了关键作用。

4 刻画定理

在基本模态逻辑的关系语义学下，van Benthem 刻画定理（[3,5]）说明，对于任意一阶公式α(x) 逻辑等值于某个模态公式的标准翻译当且仅当它在互模拟下不变。这条定理对模态语言提供了一种刻画，它使用互模拟不变这个概念刻画了基本模态语言ML 通过标准翻译嵌入到一阶语言FOL 的两变元片段FOL2：

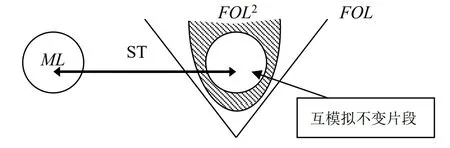
如下证明van Benthem 刻画定理对于集合论语义和集合翻译是成立的，一阶集合论公式α(x)等价于某个模态公式的集合翻译当且仅当它在集合互模拟下不变。

根据基本模态逻辑的结论和命题11，如下引理成立。

引理12.任给集合传递闭包STC({a})和STC({b})，令c 和d 分别是这两个集合传递闭包中的集合，(M,c)和(N,d)分别是那么如下三个命题等价：

(1) 对所有模态公式φ，STC({a}),c|=φ 当且仅当STC({a}),d|=φ。

(2) 集合ueSTC({a})与ueSTC({a})之间存在经典模态互模拟关系。

(3) 存在可数饱和模型(M∗,c∗) 和(N∗,d∗) 使得存在从(M,c) 到(M∗,c∗) 的初等扩张f，并且存在从(N,d) 到(N∗,d∗) 的初等扩张g 使得f(c)= c∗，g(d)=d∗，并且(M∗,c∗)与(N∗,d∗)是互模拟关系。

称一个集合论公式α(x)在集合传递闭包之间的互模拟关系下不变，若对任何两个集合传递闭包STC({a})与STC({b})，如果它们之间存在集合互模拟关系Z使得cZd，那么STC({a})|=α(x)[c]当且仅当STC({b})|=α(x)[d]。

定理13(刻画定理，[4]).令α(x)是一阶集合论公式。那么α(x)在集合互模拟下不变当且仅当它等价于某个模态公式的集合翻译。

证明.从右到左的方向容易证明，根据定理4 和命题6 即得。下面证明从左至右的方向。假设α(x)在集合互模拟下不变。考虑α(x)的所有为模态公式的集合翻译的推论集合Con(α)=π(φ,x):φ 是模态公式并且α(x)|=π(φ,x)。下面只需要证明：

(*) 如果Con(α)|=α(x)，那么α(x)等价某个模态公式的标准翻译。

原因如下：假设Con(α)|=α(x)。根据紧致性，存在有限集合X ⊆Con(α)使得X |= α(x)。所以|=∧X→α(x)。显然|= α(x)→∧X，所以∧X 作为一些模态公式合取的翻译，它等价于α(x)。下面只需要证明Con(α)|=α(x)。

假设一个集合传递闭包STC({a})|=Con(α)[c]。我们证明STC({a})|=α(x)[c]。构造集合T(x)= {π(φ,x) : STC({a}) |= π(φ,x)[c]}。首先证明T(x) ∪α(x)是一致的。假设它不一致，那么根据紧致性，存在T(x) 的有穷子集T0(x) 使得|= α(x)→¬∧T0(x)。所以¬∧T0(x)/∈Con(α)，所以STC({a}) |= ¬∧T0(x)[c]，这与STC({a})|=T(x)和T0(x)⊆T(x)矛盾。

令STC({b}) |= T(x)∪α(x)[d]。如果STC({a}),c |= φ，那么π(φ,x) ∈T(x)，所以STC({b}),d|=φ。反之，如果STC({a}),c/|=φ，那么STC({a}),c|=¬φ，所以STC({b}),d|=¬φ。由此得到：STC({a}),c|=φ 当且仅当STC({b}),d|=φ。

假设(M,c) 是由(STC({a}),c) 诱导的模型，(N,d) 是由(STC({b}),d) 诱导的模型。所以，M,c |= φ 当且仅当N,d |= φ。下面分别构造(M,c)和(N,d)的初等饱和扩张模型(M∗,c∗)和(N∗,d∗)。根据引理12，(M∗,c∗)与(N∗,d∗)互模拟，因为M,c |= φ 当且仅当N,d |= φ。由于STC({b}) |= T(x)∪α(x)[d]，所以N |= α(x)[d]。所以由初等饱和扩张，N∗|= α(x)[d∗]。再由互模拟不变条件，M∗|=α(x)[c∗]。再根据初等饱和扩张，M,c|=α(x)。

5 结语

模态逻辑的集合论语义与互模拟不变性是一个值得研究的重要问题，本文的基本思想是要在模态逻辑的集合论语义下，定义从模态语言到集合论语言的翻译，以及集合传递闭包上的互模拟概念，从而研究在集合论语言中对模态语言的刻画，所证明的定理是集合论语义下的van Benthem 刻画定理。