弱逻辑F 的矢列演算
2021-04-22陈钰
陈钰
1 引言
直觉主义逻辑(Intuitionistic Logic,简称Int)相对于满足赋值单调性的自返和传递的克里普克模型类是可靠且完全的。所谓赋值单调性,指的是如果一个命题变元p 在一个点w 上为真,那么p 在w 的每一个可及点上都为真。([4])将直觉主义逻辑的克里普克模型类扩大为满足赋值单调性的传递模型类,则可以得到一个比直觉主义逻辑更弱的逻辑——维瑟(A.Visser)在[21]中提出的基本命题逻辑(Basic Propositional Logic,简称BPL)。克罗西(G.Crosi)在[6]中研究了一些现在所说的亚直觉主义逻辑(Subintuitionistic Logics),将其称之为弱逻辑。亚直觉主义逻辑与直觉主义逻辑和基本命题逻辑一样,其蕴涵也是严格蕴涵,而非实质蕴涵。使用严格蕴涵和严格否定但不使用实质蕴涵和实质否定的命题逻辑一般也称为严格蕴涵逻辑。([9])
克罗西在[6]中给出的最弱的逻辑是F。雷斯塔尔(G.Restall)在[17]中也研究了亚直觉主义逻辑,并且其提出的逻辑SJ 与F 是等价的([22])。就F 的证明系统而言,克罗西([6])和雷斯塔尔([17])给出的是希尔伯特式公理系统。万星(H.Wansing,[22])给出了F 及其一些扩张的显示演算(Display Calculus)。塞拉特(C.Cerrato)给出了严格蕴涵逻辑的自然演绎系统。([3])石垣和鹿岛(R.Ishigaki&R.Kashima)给出了严格蕴涵逻辑的矢列演算,这些演算使用的是基于集合的矢列。([9])此外,他们运用语义的方法证明了切割规则的可容许性在这些演算中成立。马明辉和赵之光(M.Ma&Z.Zhao)使用[5]中提出的统一对应理论(unified correspondence theory)建立起严格蕴涵逻辑的模块化的无切割规则的矢列演算,而且这些演算中关于蕴涵的规则分为左引入规则和右引入规则。([12])山崎和佐野(S.Yamasaki&K.Sano)给出了F 和其他严格蕴涵逻辑的G3-型加标的矢列演算,并且证明切割规则在这些演算中是可容许的。([23])在最近的研究中,艾博利安和艾利扎德(N.Aboolian&M.Alizadeh)沿着佐佐木(K.Sasaki,[19])以及阿盖伊和阿德希尔(M.Aghaei&M.Ardeshir,[2])提出的方法,通过引入受限的实质蕴涵来刻画严格蕴涵,从而建立起F 的G3-型矢列演算GF。([1])据我所知,除此之外,没有学者给出F 的其他的G3-型(不加标的)矢列演算,但是山崎和佐野([24])以及朱吟秋([26])给出了BPL 的G3-型矢列演算G3BPL。
本文基于山崎和佐野([24])以及朱吟秋([26])给出F 的G3-型矢列演算G3F。实际上,通过对G3BPL 中的蕴涵规则(B→)进行修改就可以得到G3F 的蕴涵规则,并且G3F 的蕴涵规则严格简单于G3BPL 中的蕴涵规则。另外,这组规则都源自石井(K.Ishii)等学者在[10]中给出的BPL 的矢列演算LBP。更为重要的是,本文通过语法的方法证明切割规则在G3F 中是可容许的。众所周知,直觉主义逻辑可以通过哥德尔–麦金西–塔斯基翻译(见定义5.2)嵌入到模态逻辑S4 中。([7,13,20])本文根据特罗埃斯特拉和施维滕伯格(A.Troelstra&H.Schwichtenberg)的思路([20]),运用证明论的方法建立起从G3F 到正规模态逻辑K 的矢列演算G3K 的嵌入定理的一个新证明。嵌入定理的一个重要作用就是可以将G3F 中的切割规则的可容许性证明规约到G3K 中。另外,本文还讨论了弱逻辑F 的一些扩张及其与模态逻辑的关系。具体而言,首先建立起这些逻辑的G3-型矢列演算,然后利用证明论的方法建立它们通过哥德尔–麦金西–塔斯基翻译到模态逻辑的嵌入定理,从而证明切割规则在这些矢列演算中的可容许性。
本文结构安排如下。第2 节介绍弱逻辑F 的语言和语义。在第3 节中将给出F的G3-型矢列演算G3F,并证明切割规则在G3F 中是可容许的。第4 节将证明G3F与希尔伯特式公理系统HF 之间的等价性,从而证明G3F 的可靠性与完全性。第5 节运用证明论的方法证明弱逻辑F 可以嵌入到正规模态逻辑K 中。第6 节讨论了弱逻辑F 的一些扩张的G3-型矢列演算,并探讨了它们与模态逻辑之间的关系。第7 节是结语和将来的工作。
2 弱逻辑F
2.1 语言和语义
以下介绍弱逻辑F 的语言和语义。
定义2.1(形式语言LF).令Prop 为可数的命题变元集,定义F 的语言LF中的公式如下:

其中p ∈Prop。¬A 定义为(A→⊥), ⊤定义为¬⊥,(A ↔B) 定义为((A→B)∧(B→A))。
本文约定,公式的最外层括号可以省略。而且为了简化表达式,再约定∧,∨的联结比→优先。例如,((A∧B)→C)可以写成A∧B→C。
下面介绍F 的语义。
定义2.2(框架,模型).一个框架F 是一个有序对(W,R),其中W 是非空点集,R ⊆W ×W。框架F=(W,R)上的赋值是一函数V :Prop −→2W。
一个模型M 是一个有序对(F,V),其中V 是F 上的赋值函数。
定义2.3(公式的真).令M=(F,V)为任意模型以及w ∈W。公式A 在M 中的点w 上为真(写作M,w ⊨A)归纳定义如下:
M,w ⊨p当且仅当 w ∈V(p),其中p ∈Prop;
M,w ⊭⊥即,并非M,w ⊨⊥;
M,w ⊨A∧B 当且仅当 M,w ⊨A 并且M,w ⊨B;
M,w ⊨A∨B 当且仅当 M,w ⊨A 或者M,w ⊨B;
M,w ⊨A→B 当且仅当 对任意v ∈W,wRv,若M,v ⊨A 则M,v ⊨B。
令M=(F,V)为任意模型。如果对所有w ∈W 都有M,w ⊨A,就说公式A 在模型M 中为真(写作M ⊨A)。如果公式A 在模型M 上不真,就说公式A被模型M 反驳或者模型M 是公式A 的反模型。如果公式A 在基于框架F 的每一个模型上都为真,就说公式A 在框架F 上是有效的(写作F ⊨A)。令F 为一个框架类,如果公式A 在F 中的每一个框架上都是有效的,则说A 是F-有效的(写作F ⊨A)。
2.2 弱逻辑F 的希尔伯特式公理系统HF
现在介绍克罗西([6])给出的F 的希尔伯特式公理系统HF。
定义2.4(希尔伯特式公理系统HF).希尔伯特式公理系统HF 包含如下公理模式和推理规则:
1.A→A
2.(A→B)∧(B→C)→(A→C)
3.A∧B→A
4.A∧B→B
5.(A→B)∧(A→C)→(A→B∧C)
6.A→A∨B
7.B→A∨B
8.(A→C)∧(B→C)→(A∨B→C)
9.A∧(B∨C)→(A∧B)∨(A∧C)
10.⊥→A
推理规则

HF 中证明和定理的概念与通常定义的一样。如果公式A 是HF 的一个定理,写作⊢HFA。
定理2.1(HF 的可靠性与完全性,[6]).令FF为所有框架的类。对任意公式A 都有:⊢HFA 当且仅当FF⊨A。
3 F 的矢列演算G3F
本节将给出F 的矢列演算G3F。首先引入一些概念。
定义3.1(矢列).给定有穷的公式多重集(multiset)Γ 和∆,一个矢列是形如Γ ⇒∆的表达式,其中Γ 和∆分别称作矢列的前件和后件。
本文约定,矢列Γ∪Σ ⇒∆∪Π(其中∪表示多重集的并)简记为Γ,Σ ⇒∆,Π。例如,A,Γ,A ⇒A,∆,A,B 表示的是前件为Γ ∪{A,A},后件为∆∪{A,A,B}的矢列。另外,用≡表示两表达式相等。对有穷的公式多重集Γ,∧Γ(∨Γ)表示Γ 中所有出现的公式的任意顺序的合取(析取)。特殊地,∧∅≡⊤,∨∅≡⊥。矢列Γ ⇒∆对应的公式定义为∧Γ→∨∆。
定义3.2(子公式多重集).对任意LF公式A,A 的子公式多重集Sub(A)归纳定义如下:
• 如果A ≡p(其中p ∈Prop),那么Sub(A)={p},
• 如果A ≡⊥,那么Sub(A)={⊥},
• 如果A ≡B ∗C(其中∗∈{∧,∨,→}),那么Sub(A)={B ∗C}∪Sub(B)∪Sub(C)。
有穷的公式多重集Γ ≡A1,...,An的子公式多重集。
一个有n 个前提的规则r 有如下形式:
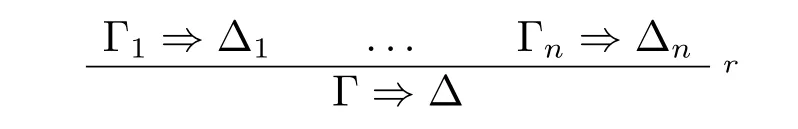
其中Γ1⇒∆1,...,Γn⇒∆n为规则r 的前提,Γ ⇒∆为r 的结论。为了书写的简便,可以把它简写成:
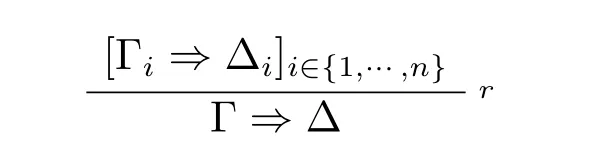
有0 个前提的规则又称公理。
现在介绍F 的矢列演算G3F。
定义3.3(G3F).G3F 的公理和规则定义如下:
公理

逻辑规则

在G3F 的公理和规则中,Γ 和∆称为语境。在一个前提数> 0 的规则的结论中,如果出现的公式在前提中有对应的真子公式出现,则称该公式为这个规则的主公式(principal formula),其对应的出现在前提中的真子公式称为活动公式(active formula)。如果出现的公式同时在前提中也出现,则称该公式为边公式(side formula)。如果出现的公式既不是主公式也不是边公式,称该公式为弱化公式(weakening formula)。特殊地,在公理中,Γ 和∆中出现的公式都是弱化公式,Id 中两次出现的公式p 都是主公式,L⊥中出现的公式⊥为主公式。在规则(→)中,C1→D1,...,Cn→Dn和A→B 都是主公式。在这里,用{Ci→Di}i∈n表示结论的前件中的这n 个主公式,因此,前件中的每一个主公式都被n 中的一个元素标记。
G3F 中的规则(→)有点复杂,现对其作出一些解释。在规则(→)中,每一个前提被n 中的一个子集索引,对s ⊆n,s 挑出指标n 中的子集,然后将被挑出的蕴含式的前件放在被s 索引的前提的后件(即{Cj}j∈s)中,同时将未被挑出的蕴含式的后件放在该前提的前件(即{Dk}k∈ns)中。容易看出,该规则的前提数量由n 决定,即如果该规则结论的前件中有n 个主公式,则该规则的前提数量为2n。再通过一些例子进行说明。当n=0,1,2 时,规则(→)的形式分别如下所示:

注1.正如在引言中提到的,本文是通过对山崎和佐野([24])和朱吟秋([26])给出的G3BPL 中的蕴涵规则进行修改而得到G3F 的蕴涵规则。因此,只需要将G3F中的规则(→)替换为如下规则(B→)就可以得到G3BPL:

注2.石垣和鹿岛([9])给出了F 的矢列演算GKI并且证明了它的可靠性与完全性。而克罗西([6])证明了HF 的可靠性和完全性,因此,易知GKI和HF 是等价的。根据本文在第4 节中证明的G3F 与HF 之间的等价性可知,GKI与G3F 是等价的。
GKI使用集合矢列。而G3F 使用多重集矢列,是[15,20]中的G3-型演算。G3-型演算的一个特点就是将结构规则吸收在公理和逻辑规则中。另外,本文与[9]最重要的一个区别是,本文给出了G3F 中切割规则可容许性的纯语法的证明,这也是本文的主要贡献之一,而[9]则是通过语义的方法证明切割规则在GKI中是可容许的。
定义3.4(“矢列的”证明).G3F 中的一个证明是一棵有穷的有向树,该树的每一个节点上都是矢列,并且每个节点上的矢列作为结论,与其所有子节点上的矢列作为前提,构成对G3F 中一规则的一个运用。每一个证明被称为其根矢列的证明,并且0 前提规则的结论是证明(树)的叶子。一个证明的高度h 是该证明(树)中最长有向路径的节点之间的距离,其中公理的高度为0。矢列Γ ⇒∆在G3F 中是可证的(写作⊢G3FΓ ⇒∆)当且仅当Γ ⇒∆在G3F 中有一个证明。此外,用⊢hΓ ⇒∆表示Γ ⇒∆在G3F 中有一个高度至多为h 的证明。
容易观察到,在G3F 的规则中,前提中出现的每个公式都是结论中出现的公式的子公式。因此,G3F 具有子公式性质。
命题3.1(子公式性质).如果Γ ⇒∆在G3F 中有一个证明,那么该证明中出现的每一个公式都是Γ,∆的子公式。
这样,给定一个矢列Γ ⇒∆,可以在G3F 中构造一棵从下到上的证明搜索树,因而F 是可判定的。
定义3.5(规则的可容许、保高可容许、保高可逆).对任意规则r,(1)如果该规则的所有前提在G3F 中是可证的蕴涵其结论在G3F 中也是可证的,则称规则r 在G3F中是可容许的。如果该可容许规则r 还满足:若其前提在G3F 中有高度≤h 的证明,其结论在G3F 中也有高度≤h 的证明,则称该规则在G3F 中是保高可容许的。(2)如果该规则的结论在G3F 中有高度≤h 的证明蕴涵其所有前提在G3F 中也有高度≤h 的证明,则称该规则在G3F 中是保高可逆的。
定义3.6(公式的度).一个公式A 的度(degree)dg(A)定义如下:
• dg(⊥)=0,
• dg(p)=1,其中p ∈Prop,
• dg(A ∗B)=dg(A)+dg(B)+1,其中∗∈{∧,∨,→}。
定义3.7(切割规则).切割规则(Cut)定义如下:
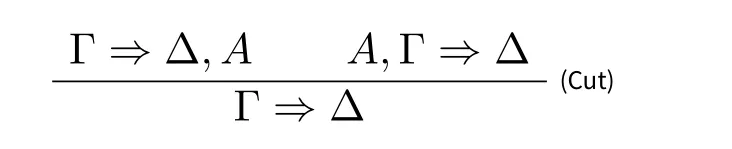
其中公式A 称为切割公式。切割公式的度称为(Cut)的秩(rank),(Cut)的前提的证明高度之和称为(Cut)的级(level)。
如果(Cut)的秩为r 且级为l,则其等级d(grade)为ω·r+l(其中ω 为最小的无穷序数)。用表示将(Cut)的等级限制为≤ω·r+l,G3F⊕(Cut)rl表示通过受限等级的扩张G3F 得到的演算,G3F⊕(Cut)表示通过不受限等级的(Cut)扩张G3F 得到的演算。
接下来将证明切割规则在G3F 中是可容许的,这也是本文的一个主要定理。但在这之前,首先证明一些需要用到的引理。
引理3.1.对任意公式A,都有:⊢G3FA,Γ ⇒∆,A。
证明.施归纳于公式A 的复杂度。考虑A ≡B→C 的情形,那么最后一步如下所示:
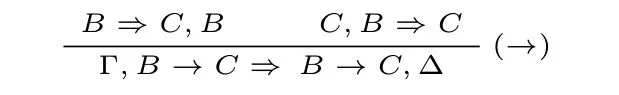
运用归纳假设,B ⇒C,B 和C,B ⇒C 是可证的。因此Γ,B→C ⇒ B→C,∆也是可证的.
引理3.2(弱化规则保高可容许).令Γ,∆为公式多重集,A 为LF中的公式。在G3F或(其中r,l ∈N)中,有
(1) 如果⊢hΓ ⇒∆,那么⊢hA,Γ ⇒∆。
(2) 如果⊢hΓ ⇒∆,那么⊢hΓ ⇒∆,A。
证明.选证(1)。(2)的证明与(1)类似。施归纳于h。如果h=0,那么Γ ⇒∆是公理,因此A,Γ ⇒∆也是公理。
如果h > 0。如果在Γ ⇒∆的证明中,最后运用的规则是L∧,R∧,L∨,R∨或中的一个,那么先运用归纳假设于前提中,再对得到的结果运用该规则即可。
如果最后运用的规则是(→)。不失一般性,令Γ ≡Γ′,{Ci→Di}i∈n以及∆≡E→F,∆′,那么有:

由于[⊢h−1{Dk}k∈ns,E ⇒F,{Cj}j∈s]s⊆n,则运用规则(→)得到⊢hΓ′′,{Ci→Di}i∈n⇒E→F,∆′,其中Γ′′≡A,Γ′。
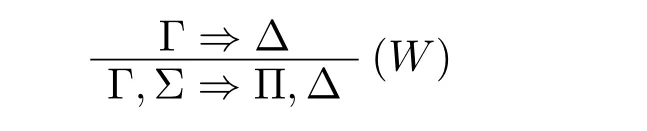
在证明收缩规则保高可容许之前,先引入如下可逆引理。
引理3.3(可逆引理).在G3F 或G3F⊕(Cut)rl(其中r,l ∈N)中,除规则(→)外的所有逻辑规则都是保高可逆的。
证明.选证规则L∨是保高可逆的,其余规则的证明类似。因此只需证:如果⊢hA∨B,Γ ⇒∆,那么有:⊢hA,Γ ⇒∆以及⊢hB,Γ ⇒∆。
施归纳于h。如果h=0,那么A∨B,Γ ⇒∆是公理,则A,Γ ⇒∆和B,Γ ⇒∆也是公理。
如果h>0。如果A∨B 是主公式或弱化公式,显然。
如果A∨B 是边公式,则最后运用的规则不可能是公理或(→),则直接运用归纳假设于该规则的前提,然后对得到的结果运用该规则即可。
引理3.4(收缩规则保高可容许).令Γ,∆为公式多重集,A 为LF中的公式。在G3F或(其中r,l ∈N)中,有
(1) 如果⊢hA,A,Γ ⇒∆,那么⊢hA,Γ ⇒∆。
(2) 如果⊢hΓ ⇒∆,A,A,那么⊢hΓ ⇒∆,A。
证明.同时施归纳于(1)和(2)中的h。如果h=0,显然。
如果h>0。(1)如果A 的两次出现的其中一次是弱化公式,则在运用同样的规则于前提得到的结论中且不引入A 作为弱化公式即可。如果A 的两次出现都是边公式,则最后运用的规则一定是L∧,R∧,L∨,R∨或中的一个,那么由归纳假设易得。如果A 的两次出现其中一次是边公式,另一次是主公式,则最后运用的规则一定是L∨或L∧,则根据引理3.3 和归纳假设可得。如果A 的两次出现都是主公式。不妨令其分别为Cu→Du,Cv→Dv,则有

其中Γ′,{Ci→Di}i∈n{u,v}≡Γ 以及E→F,∆′≡∆。
这时有:对任意r ⊆n,如果u,v/∈r,则有

由归纳假设得⊢h−1{Dk}k∈(n ){u,v},Du,E ⇒F,{Cj}j∈r,
因此有[⊢h−1{Dk}k∈n {u,v},Du,E ⇒F,{Cj}j∈r]r⊆(n{u,v});
对任意t ⊆n,如果u,v ∈t,则有

由归纳假设得⊢h−1{Dk}k∈n ,E ⇒F,Cu,{Cj}j∈t{u,v}。
因此有[⊢h−1{Dk}k∈n ,E ⇒F,Cu,{Cj}j∈t{u,v}]u,v∈t,t⊆n;
运用规则(→)可以得到Γ′,{Ci→Di}i∈n{u,v},Cu→Du,⇒E→F,∆′。
(2) 如果A 的两次出现的其中一次是弱化公式或者边公式,证明与(1)类似。如果A 的两次出现都是主公式,但这显然不可能,因为G3F 或的规则没有结论的后件出现两个(及两个以上)主公式的情况。
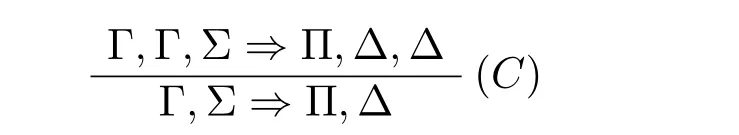
定理3.5.规则(Cut)在G3F 中是可容许的。
证明.对(Cut)的秩和级进行双重归纳。由于A 在左右前提中的每一次出现可以是主公式、边公式或弱化公式中的一种,因此有以下三种情况:
情况1:A 在(Cut)的左前提或右前提中为弱化公式。显然有Γ ⇒∆。
情况2:A 在(Cut) 的左前提或右前提中为边公式。由于规则(→) 没有边公式出现,因此得到左或右前提的最后一步运用的规则必定是L∧,R∧,L∨,R∨或秩 然后将(Cut)规则的运用向上置换可以得到 情况3:A 在(Cut)的左前提和右前提中都为主公式。考虑A 是蕴含式的情况,不妨令A ≡Cz→Dz,Γ ≡Θ,{Gi′→Hi′}i′∈n≡Π,{Ci→Di}i∈m,∆≡E→F,Σ,则有 将[{Dk}k∈m ,E ⇒F,{Cj}j∈t]t⊆m划分成两部分:[{Dk}k∈(m{z}) ,E ⇒F,Cz,{Cj}j∈t]t⊆m{z}以及[Dz,{Dk}k∈(m{z}) ,E ⇒F,{Cj}j∈t]t⊆m{z}。容易知道,这两部分包含的矢列数量皆为2m−1。 对任意s ⊆n 以及t ⊆m {z},令Λ1≡{Dk}k∈(m{z}) ,E 以及Λ2≡F,{Cj}j∈t,则可以得到: 然后有 由于有2n+m−1个上述形式的子证明,因此其结论也有2n+m−1个。 现在令n′= {1,...,n,n+1,...,n+z −1,n+z +1,...,n+m}。对任意i′′∈n′,定义Gi′′和Hi′′如下: 然后有 因此有Θ,{Gi′→Hi′}i′∈n,Π,{Ci→Di}i∈m{z}⇒E→F,Σ,运用规则(C)可以得到Θ,{Gi′→Hi′}i′∈n⇒E→F,Σ。 本节证明矢列演算G3F 与希尔伯特式公理系统HF 是等价的。 引理4.1.对任意公式A,如果⊢HFA,那么⊢G3F⇒A。证明.施归纳于HF 中公式A 的证明结构。容易看到,对HF 中的所有公理A,都有⊢G3F⇒A。例如,(A→B)∧(A→C)→(A→B∧C)在G3F 中的一个证明如下所示: (AF) 的情形是平凡的。至于(MP),假设⊢G3F⇒Ai(其中1 ≤i ≤n)和⊢G3F⇒A1∧···∧An→B,运用有穷多次规则R∧得到⊢G3F⇒A1∧···∧An,因此有⊢G3F⇒A1∧···∧An,B。而得到⇒A1∧···∧An→B 最后一步运用的规则一定是(→),因此⊢G3FA1∧···∧An⇒B。运用规则(Cut)可以得到⊢G3F⇒B。 在证明引理4.1 的相反方向之前,需要证明一系列引理。 引理4.2.对任意公式A,B,如果⊢HFA 以及⊢HFB,那么⊢HFA∧B。 证明.运用(MP)到⊢HFA,⊢HFB 以及⊢HFA∧B→A∧B 即可。 引理4.3([6]).对任意公式A,B,C, 如果⊢HFA→B 以及⊢HFB→C, 那么⊢HFA→C。 证明.假设⊢HFA→B 和⊢HFB→C。根据引理4.2 有⊢HF(A→B)∧(B→C)。因为⊢HF(A→B)∧(B→C)→(A→C)。运用(MP)可得⊢HFA→C。 引理4.4.对任意公式A,B,C,D,如果⊢HFA→B,那么⊢HFA∧C→B∨D。 证明.假设⊢HFA→B。因为⊢HFA∧C→A,根据引理4.3 有⊢HFA∧C→B,又⊢HFB→B∨D,再根据引理4.3有⊢HFA∧C→B∨D。 引理4.5.对任意公式A,B,C, 如果⊢HFA→B 和⊢HFA→C, 那么⊢HFA→B∧C。 证明.假设⊢HFA→B 和⊢HFA→C。由于⊢HF(A→B)∧(A→C)→(A→B∧C),运用(MP)得⊢HFA→B∧C。 引理4.6.对任意公式A,B,C,D,如果⊢HFA→(B→C)和⊢HFA→(C→D),那么⊢HFA→(B→D)。 证明.假设⊢HFA→(B→C)和⊢HFA→(C→D),根据引理4.5,可以得到⊢HFA→(B→C)∧(C→D)。又因为⊢HF(B→C)∧(C→D)→(B→D),根据引理4.3,可得⊢HFA→(B→D)。 引理4.7.对任意公式A,B,C,D1,D2,如果⊢HFA→B∨C,⊢HFB→D1和⊢HFC→D2,那么⊢HFA→D1∨D2。 证明.假设⊢HFB→D1和⊢HFC→D2,则易知⊢HFB∨C→D1∨D2。又因为⊢HFA→B∨C,根据引理4.3 得⊢HFA→D1∨D2。 引理4.8.对任意公式A,B,C,D1,D2,如果⊢HFA→(B→C∨D1)和⊢HFA→(B→C∨D1),那么⊢HFA→(B→C∨(D1∧D2))。 证明.首先证明⊢HF(C∨D1)∧(C∨D2)→C∨(D1∧D2)。 因为⊢HF(C∨D1)∧(C∨D2)→((C∨D1)∧C)∨((C∨D1)∧D2),⊢HF(C∨D1)∧C→(C∧C)∨(C∧D1),⊢HF(C∨D1)∧D2→(C∧D2)∨(D1∧D2),由引理4.7 得⊢HF(C∨D1)∧(C∨D2)→(C∧C)∨(C∧D1)∨(C∧D2)∨(D1∧D2)。易知⊢HFC∧C→C,⊢HFC∨(C∧Di)→C(其中i ∈{1,2}),可得⊢HF(C∨D1)∧(C∨D2)→C∨(D1∧D2)。 假设⊢HFA→(B→C∨D1)和⊢HFA→(B→C∨D1),易知⊢HFA→(B→(C∨D1)∧(C∨D2))。又因为⊢HFA→((C∨D1)∧(C∨D2)→C∨(D1∧D2)),根据引理4.6 可得⊢HFA→(B→C∨(D1∧D2))。 引理4.9([6]).对任意公式A,B,C,如果⊢HFA→B,那么⊢HF(C→A)→(C→B)。 证明.假设⊢HFA→B。运用(AF) 可以得到⊢HF(C→A)→(A→B)。因为⊢HF(C→A)→(C→A),那么根据引理4.5 有⊢HF(C→A)→((C→A)∧(A→B))。因为⊢HF(C→A)∧(A→B)→(C→B),由引理4.3 可得⊢HF(C→A)→(C→B)。 引理4.10.对任意公式A,B 以及k ∈n={1,...,n},如果⊢HF∧{Ci→Di}i∈n→(A→B∨Ck)那么⊢HF∧{Ci→Di}i∈n→(A→B∨Dk)。 证明.首先,(Ck→Dk)→((B→B∨Dk)∧(Ck→B∨Dk)在HF 中的证明如下: 因为⊢HF(B→B∨Dk)∧(Ck→B∨Dk)→(B∨Ck→B∨Dk)以及⊢HF∧{Ci→Di}i∈n→(Ck→Dk),根据引理4.3 有⊢HF ∧{Ci→Di}i∈n→(B∨Ck→B∨Dk)。此外,⊢HF∧{Ci→Di}i∈n→(A→B∨Ck),然后根据引理4.5有⊢HF∧{Ci→Di}i∈n→((A→B∨Ck)∧(B∨Ck→B∨Dk))。又因为⊢HF(A→B∨Ck)∧(B∨Ck→B∨Dk)→(A→B∨Dk),根据引理4.3 可以得到⊢HF∧{Ci→Di}i∈n→(A→B∨Dk)。 引理4.11.对任意公式A,B,C 和D,如果⊢HFC→(A∧D→B)那么⊢HFC→(A∧(B∨D)→B)。 证明.首先考虑HF 中的如下证明: 由于⊢HF(A∧B→B)∧(A∧D→B)→((A∧B)∨(A∧D)→B),然后根据引理4.3,可以得到⊢HFC→((A∧B)∨(A∧D)→B)。然后有 由于⊢HF(A∧(B∨D)→(A∧B)∨(A∧D))∧((A∧B)∨(A∧D)→B)→(A∧(B∨D)→B),根据引理4.3 得到⊢HFC→(A∧(B∨D)→B)。 引理4.12.对任意公式A,如果⊢G3F⇒A,那么⊢HFA。 证明.令∧Γ(∨Γ)为Γ中∧所有公∨式的合取(析取)。证明对任意矢列Γ ⇒∆,如果⊢G3FΓ⇒∆那么⊢HFΓ→∆。 施归纳于Γ ⇒∆在G3F 中的证明高度。这里只考虑规则为(→)时的情况。根据归纳假设,对所有s ⊆n,有⊢HF∧({Dk}k∈ns,A)→∨(B,{Cj}j∈s)。然后运用有穷多次(AF)可得,对任意s ⊆n,有⊢HF ∧{Ci→Di}i∈n→(∧({Dk}k∈ns,A)→∨(B,{Cj}j∈s))。然后多次运用引理4.10 可得:对所有s ⊆ n,⊢HF∧{Ci→Di}i∈n→(∧({Dk}k∈ns,A)→∨(B,{Dj}j∈s))。因此只需证: 然后取s=∅,即可得到⊢HF∧{Ci→Di}i∈n→(A→B)。最后运用有穷多次引理4.4,有⊢HF∧(Γ,{Ci→Di}i∈n)→∨(A→B,∆)。 现在证明(#)。首先根据基数大小将n 的所有子集按如下顺序排列: 令sm是n 的第m(1 ≤m ≤2n)个子集。施归纳于m。 如果m=1,显然有⊢HF∧{Ci→Di}i∈n→(A→∨(B,{Dj}j∈n)),因为{Dk}k∈ns=∅。 如果m > 1。由于⊢HF∧{Ci→Di}i∈n→(∧({Dk}k∈nsm,A)→∨(B,{Dj}j∈sm)),根据 引理4.11 可得令Dk1,Dk2,...,Dkk′为{Dk}k∈nsm中公式的一个枚举。则对任意1 ≤l ≤k′,存在m′ 因此根据引理4.1 和引理4.12 可以得到G3F 和HF 之间的等价性。 命题模态语言L□由语言LF加上模态算子□组合而成。所有其他逻辑联结词以及模态算子◇与通常的定义一样。 现在介绍正规模态逻辑K 的矢列演算G3K。 定义5.1(G3K).G3K 的公理和规则定义如下: 公理 逻辑规则 其中□Θ={□B |B ∈Θ}。 模态逻辑K 的矢列演算首先由莱万特(D.Leivant,[11]),敏兹(G.Mints,[14])以及桑宾和瓦伦蒂尼(G.Sambin&S.Valentini,[18])给出。不过他们给出的矢列演算是基于集合的矢列而不是多重集的矢列,而且模态算子□的规则如下式: G3K 中主公式、边公式、弱化公式、证明、证明的高度以及规则的(保高)可容许等的定义与G3F 中的类似。此外,易知弱化、收缩和切割规则在G3K 中是可容许的。([8]) 现在介绍哥德尔–麦金西–塔斯基翻译。([20]) 定义5.2(翻译τ). 令Γ ≡A1,···,An为有穷的公式多重集,定义Γτ:=,···,。 接下来将运用证明论的方法证明弱逻辑F 可以通过哥德尔–麦金西–塔斯基翻译嵌入到模态逻辑K 中,即:对LF中的每个公式A, 注3.克罗西([6])定义了一个翻译∗,其与翻译τ 的不同之处仅在于对原子命题的翻译:p∗:=p,并且通过模型论的方法证明F 可以通过翻译∗嵌入到模态逻辑K 中。而本文通过证明论的方法给出F 通过翻译τ 嵌入到模态逻辑K 的新证明。 注4.山崎和佐野([23])定义了哥德尔–麦金西–塔斯基翻译的一个变种翻译τ′,由于他们给出的是是加标的矢列演算,因此与τ 的不同之处除对原子命题的翻译(pτ′:=p∧□p)外,还引入了对加标公式x:A 的翻译:(x:A)τ′:=x:Aτ′,以及对关系原子公式xRy 的翻译:(xRy)τ′:= xRy。然后他们证明F 的G3-型加标矢列演算LG3F 可以通过翻译τ′嵌入到模态逻辑K 的G3-型加标矢列演算LG3K 中。而本文的证明使用的是不加标的矢列演算。 为证明(∗∗∗),只需证明更一般的形式:⊢G3FΓ ⇒∆当且仅当⊢G3KΓτ⇒∆τ,其中Γ 和∆为有穷的LF-公式多重集。 引理5.1.令Γ 和∆为有穷的LF-公式多重集。如果⊢G3FΓ ⇒∆,那么⊢G3KΓτ⇒∆τ。 证明.施归纳于G3F 中Γ ⇒∆的证明高度h。 如果h=0。那么Γ ⇒∆是公理,则显然有⊢G3KΓτ⇒∆τ。 如果h > 0。考虑最后一步运用的规则是(→) 的情况。令Γ ≡Γ′,{Ci→Di}i∈n以及∆≡A→B,∆′,那么有: 然后取m=n,可得(⋆⋆)。 现在证明(⋆⋆⋆)。施归纳于m。当m=0 时,由(⋆)直接可得。 假设m=k′时有: 其中k′={1,...,k′}。而其可以划分为两部分: 其中k′′={1,...,k,k+1}。因此有: 引理5.2.令Π 为有穷的原子公式集,p ∈Prop,Γ 为有穷的L□-公式集且Γ ∩(Prop ∪{⊥})=∅,则如果⊢G3KΠ,Γ ⇒p,那么⊢G3KΠ ⇒p。 证明.施归纳于证明的高度易得。 引理5.3.令Π 为有穷的原子公式集,Θ1和Θ2为有穷的L□-公式集且Θi∩Prop=∅(i ∈{1,2}),则如果⊢G3KΠ,Θ1⇒Θ2,那么⊢G3KΘ1⇒Θ2。 证明.施归纳于证明的高度易得。 引理5.4.令Γ 和∆为有穷的LF-公式多重集,Π 和Σ 为有穷的原子公式多重集。如果⊢G3KΓτ,Π ⇒∆τ,Σ,那么⊢G3FΓ,Π ⇒∆,Σ。 证明.施归纳于G3K 中Γτ,Π ⇒∆τ,Σ 的证明高度h. 如果h=0。那么Γτ,Π ⇒∆τ,Σ 在G3K 中是公理,因此Γ,Π ⇒∆,Σ 在G3F也是公理。 如果h>0。注意到Π,Σ 是LF中的有穷的原子公式多重集,而Γτ和∆τ中的公式的最外层联结词一定不是蕴涵符号→。因此考虑如下情况: (i)最后运用的规则是(L∧),(R∧),(L∨)或(R∨), (ii)最后运用的规则是(K□)。 情况(i),考虑最后运用的是(R∧),其余情况类似。令∆τ≡Aτ∧Bτ,∆′τ,那么有 由归纳假设知,⊢G3FΓ,Π ⇒A,Σ 以及⊢G3FΓ,Π ⇒B,Σ,运用规则R∧可得⊢G3FΓ,Π ⇒A,Σ。 情况(ii)。由于最后运用的规则是(K□),则主公式一定是模态前束公式。令Γτ≡Γ′τ,□Π′,以及∆τ≡□A,∆′τ,其中Π′为有穷的原子公式多重集,则有 若A ≡p,则根据引理5.2 有⊢G3KΠ′⇒p,由归纳假设得⊢G3FΠ′⇒p,运用(W)得⊢G3FΓ′,Π′,{Ci→Di}i∈n,Π ⇒p,∆′,Σ。 基于引理5.1和引理5.4,有如下定理: 定理5.5.令Γ 和∆为有穷的LF-公式多重集。那么⊢G3FΓ ⇒∆当且仅当⊢G3KΓτ⇒∆τ。 上述定理的一个运用就是可以用来证明切割规则(Cut)在G3F 中的可容许性。 定理5.6.规则(Cut)在G3F 中是可容许的。 证明.假设⊢G3FΓ ⇒∆,A 以及⊢G3FA,Γ ⇒∆,根据定理5.5 可得⊢G3KΓτ⇒∆τ,Aτ和⊢G3KAτ,Γτ⇒∆τ。又因为切割规则(Cut)在G3K 中是可容许的,因此有⊢G3kΓτ⇒∆τ。因此,⊢G3FΓ ⇒∆。 本文建立的这种G3-矢列演算可以扩展到弱逻辑F 的一些扩张上,比如克罗西([6])建立的逻辑FD、FR 以及FT 上。这三个逻辑希尔伯特式公理系统分别是在HF 的基础上增加如下公理D′、T′以及4′得到: 与之对应的G3-型矢列演算G3D′和G3T′分别是在G3F 的基础上增加如下规则(→d),(→t)得到: 而将G3F 中的规则(→)修改为如下规则(→4)并保持公理和其他规则不变,就可以得到逻辑FT 的矢列演算G34′: 克罗西([6])运用模型论的方法证明了FD、FR 以及FT 可以通过翻译∗分别嵌入到模态逻辑D、T 以及K4 中。本文则运用证明论的方法证明FD、FR 以及FT可以通过哥德尔–麦金西–塔斯基翻译分别嵌入到模态逻辑D、T 以及K4 中。 为此,先给出模态逻辑D、T 以及K4 的G3-型矢列演算G3D、G3T 和G34。G3D、G3T 分别在G3K 的基础上增加如下规则(D□)和(L□)得到: 将G3K 中的规则(K□)修改为如下的规则(4□)就可以得到矢列演算G34: 矢列演算G3D、G3T 和G34 同样具有良好的证明论性质,即弱化、收缩和规则(Cut) 都是可容许的。([16,25])用G3[D′T′4′]表示一个矢列演算X ∈{G3D′,G3T′,G34′},G3[DT4]类似。与第5 节中的证明类似,可以得到: 定理6.1.⊢G3[D′T′4′]Γ ⇒∆当且仅当⊢G3[DT4]Γτ⇒∆τ。 运用定理6.1,可以得到: 定理6.2.规则(Cut)在G3[D′T′4′]中是可容许的。 本文建立起弱逻辑F 的矢列演算G3F,并且证明结构规则(弱化、收缩和切割规则)在该演算中是可容许的。事实上,本文给出了G3F 中切割规则可容许性的一个纯语法的证明。同时,也证明了矢列演算G3F 与希尔伯特式公理系统HF 是等价的。此外,本文运用证明论的方法给出一个通过哥德尔–麦金西–塔斯基翻译将弱逻辑F 嵌入到模态逻辑K 的新证明,并给出了F 的一些扩张的G3-型矢列演算,探讨了它们与模态逻辑之间的关系,即建立起它们到模态逻辑的嵌入定理。 在将来的工作中,我们考虑将本文的方法扩展到其他严格蕴涵逻辑,以此建立起这些逻辑的无切割规则的G3-型矢列演算。另外,切割消去定理的一个应用就是给出克雷格内插性质(Craig Interpolation Property,简称CIP)甚至比其更强的林登内插性质(Lyndon Interpolation Property,简称LIP)的构造性证明。艾博利安和艾利扎德([1])根据阿盖伊和阿德希尔([2])证明BPL 具有CIP 的方法,给出与GF 等价的一个变种矢列演算GFs,在该演算中矢列的后件至多含有一个公式,从而构造性的方法证明了F 具有LIP。然而,这类方法都是借助扩张的语言,即引入受限的实质蕴涵,来刻画严格蕴涵,从而实现目的。但是本文建立的矢列演算不引入额外的语言,因此,能否根据本文的这类演算,运用证明论的方法给出F 以及其他严格蕴涵逻辑的内插性质(如果有的话)的构造性证明也是一项有意义的工作。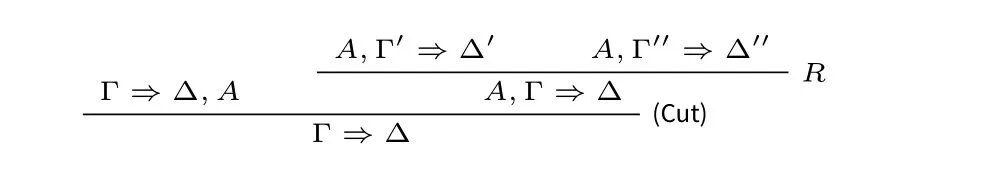


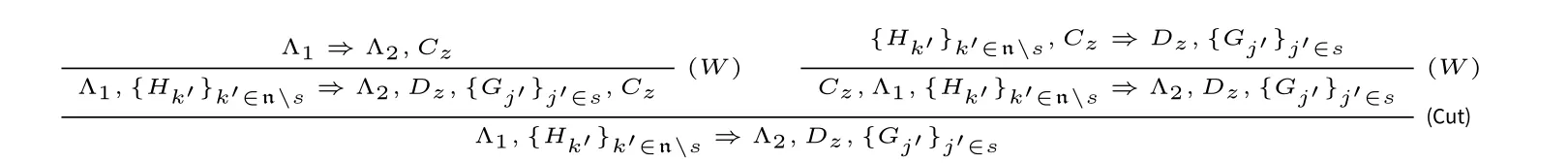

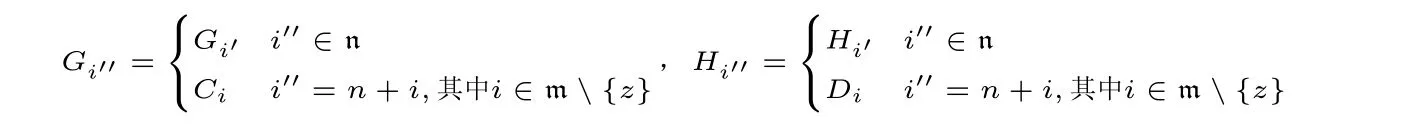
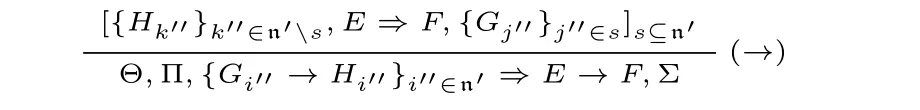
4 G3F 与HF 之间的等价性







5 F 到模态逻辑K 的嵌入定理

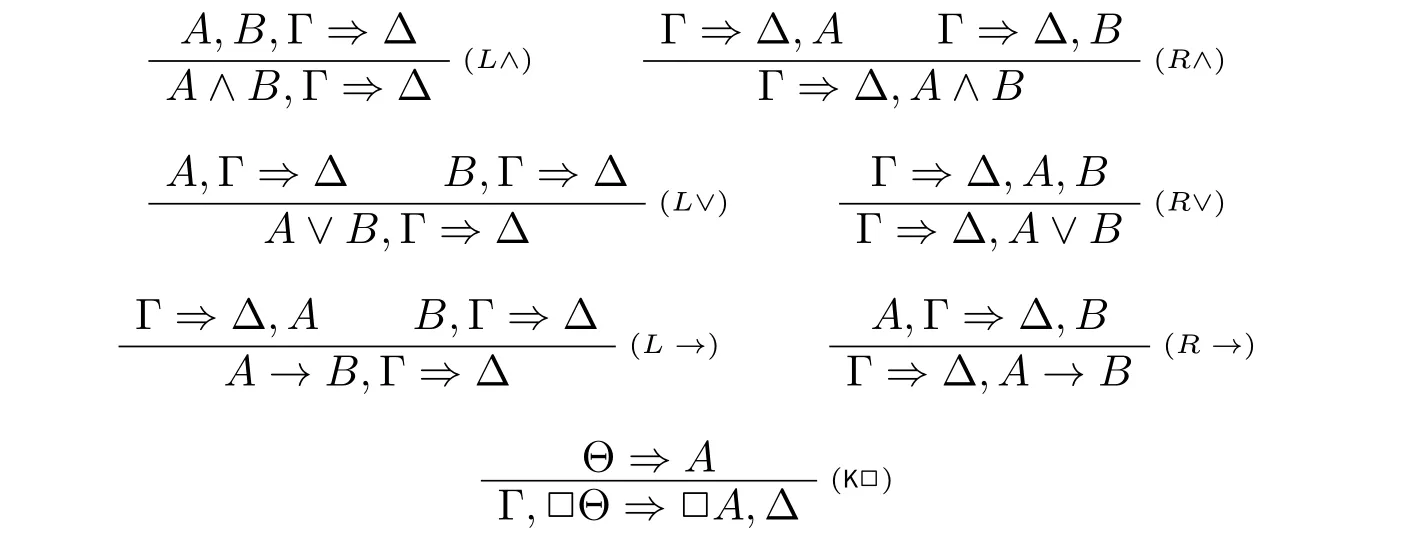


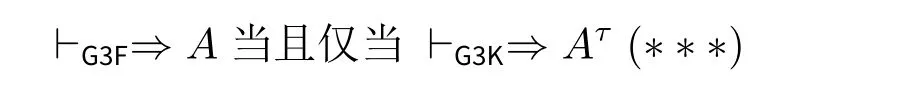

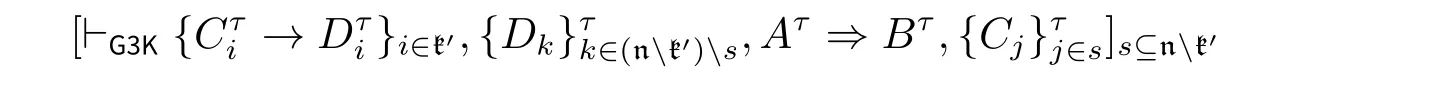


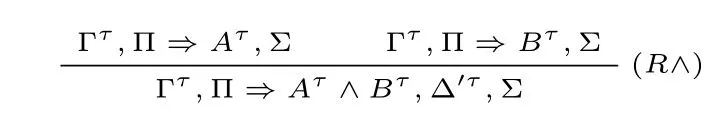


6 讨论
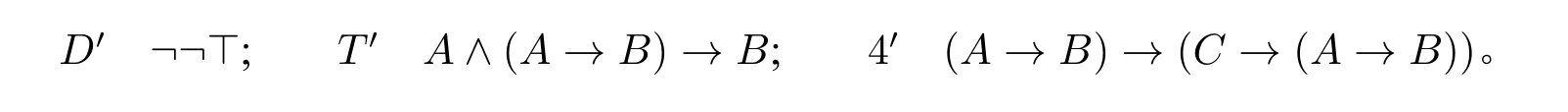



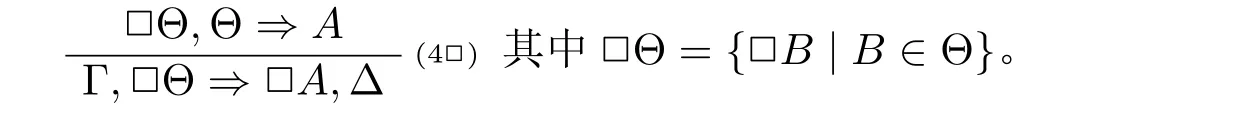
7 结语
