2019年高考北京卷文科第19题的探究与变式

河北省秦皇岛市第一中学(066006) 赵成海 张 瑞 吕东毓

一、题目再现

题目(2019年高考北京卷文科第19 题) 已知椭圆=1 的右焦点为(1,0),且经过点A(0,1).

(Ⅰ)求椭圆C的方程;(答案:+y2=1)

(Ⅱ)设O为原点,直线l:y=kx+t(t /=±1)与椭圆C交于两个不同点P,Q,直线AP与x轴交于点M,直线AQ与x轴交于点N,|OM|·|ON|=2,求证: 直线l经过定点.

二、寻求考题解法的思考策略

定点问题,一般有两种入手方法,一是设直线方程,通过直曲联立及二次方程根与系数的关系寻求解决方法;二是设点坐标,寻求迂迴求解方法.

思考一(以直线l为切入点,通过直曲联立,直接求解)由得:(1+2k2)x2+4ktx+2t2−2=0,Δ = 16k2t2−4(1+2k2)(2t2−2)＞0, 得t2＜2k2+1,设P(x1,y1), Q(x2,y2), 由根与系数的关系:x1+x2=则y1+y2=k(x1+x2)+2t=因为A(0,1), 所以直线AP方程为:y=+1, 故同理由|OM| · |ON|=2,解得t=0,那么直线l经过原点.

评注这种解法, 充分体现考试说明中的“注重常规”.在数学学科核心素养中,“数学运算”是指在清晰运算对象的基础上,依据运算法则解决数学问题.本解法最贴近学生实际,充分体现对“数学运算”的考查.

思考二(以M,N坐标作为切入点, 化归转化, 迂回求解) 设M(m,0),N(n,0), 直线AM:y=由得: (m2+ 2)x2−4mx= 0, 所以xP=同理, 直线AN:y=+ 1.由因为|OM|·|ON|=2,所以mn=±2, 当mn= 2 时,xP −xQ== 0, 从而直线l斜率不存在, 矛盾; 当mn=−2 时,xP+xQ=

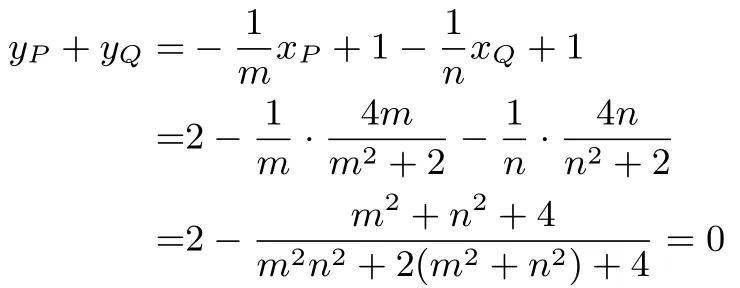
所以P,Q两点关于原点对称,所以直线l经过原点.

评注在数学学科核心素养中,“数据分析”是指针对研究对象获取数据,运用数学方法进行整理、分析和推断,形成关于研究对象知识的素养.本解法就是将直线过定点问题,转化为在|OM|·|ON|= 2 条件下, 获取xP −xQ= 0 及xP+xQ=0 这两个数据,从而判断直线l斜率不存在,或者恒过原点,而斜率不存在时是不合题设的,因而合理推断,获得题目要证的结论.

三、对考题的深入思考与探究

1 探究一般性

题中|OM|·|ON|= 2 是本题的关键所在,是针对具体椭圆+y2= 1 的一个特例,那么这里的“2”与椭圆方程有什么关系呢? 不难发现恰好与椭圆中的a2=2 相一致,这是偶然吗? 能否可以猜想对于= 1(a ＞b ＞0),当|OM|·|ON|=a2具有同样的特点? 经过探究我们得到如下结论:

性质1已知椭圆C:= 1 的上顶点为点A,O为坐标原点,直线l与椭圆C交于两个不同的点P,Q(异于椭圆C的上下顶点),直线AP与x轴交于点M,直线AQ与x轴交于点N,若|OM|·|ON|=a2,则直线l经过原点或者斜率不存在.

证明设M(m,0),N(n,0), 因为A(0,b), 所以直线AM:y=+b, 与椭圆C联立得: (m2+a2)x2−2a2mx= 0, 所 以xP=同理,xQ=|OM| · |ON|=a2, 所以mn=±a2,当mn=a2时,xP −xQ== 0, 从而直线l斜率不存在; 当mn=−a2时,xP+xQ=

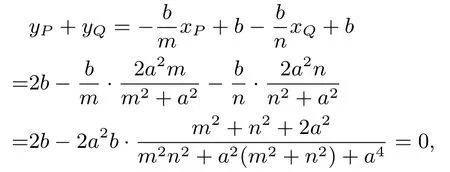
所以P,Q两点关于原点对称,即直线l经过原点.

评注在数学学科核心素养中,“逻辑推理”是指从一些事实和命题出发,依据规则推出其他命题的素养.本探究与分析,显然体现从特殊到一般的推理思想,这就是类比、归纳,然后进行证明.

2 探究完备性

进一步思考,性质1 的逆命题也是成立的.

性质2已知椭圆C:= 1 的上顶点为点A,O为坐标原点,直线l与椭圆C交于两个不同的点P,Q(异于椭圆C的上下顶点),直线AP与x轴交于点M,直线AQ与x轴交于点N,则|OM|·|ON|=a2的充要条件是: 直线l经过原点或者斜率不存在.

简析结合性质1 的证明, 若直线l经过原点, 则由对称性知xP+xQ=0,即xP+xQ== 0,mn2+a2m+m2n+a2n=0,整理得(m+n)(mn+a2)=0,由于m+n/=0,所以mn=−a2.

若直线l斜率不存在, 则xP=xQ, 即,mn2−a2m+m2n−a2n=0,整理得(m+n)(mn−a2)=0,所以mn=a2,所以|OM|·|ON|=a2成立.

评注在数学学科核心素养中,“逻辑推理”是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质.对逆命题的分析与研究,正是这一思维品质的体现.

3 挖掘题目源头

教材例题(人教版选修2-1 第41 页例3): 如图所示, 设点A,B的坐标分别为(−5,0),(5,0),直线AM,BM相交于M,它们的斜率之积是求点M的轨迹方程.

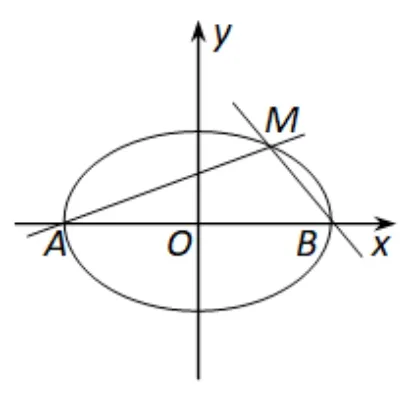
本题容易求得点M的轨迹方程为椭圆:1(x/=±5),教学过程中,曾得出过一般性结论:

结论1已知A,B是椭圆= 1(a ＞b ＞0)长轴的两个端点,P点是椭圆上与A,B两点均不同的点,那么kPA·kPB=

这一结论易证: 由已知A(−a,0),B(a,0), 设P(x,y),则= 1, 移项整理得:即kPA·kPB=

结论2已知A,B是椭圆= 1(a ＞b ＞0)短轴的两个端点,P点是椭圆上与A,B两点均不同的点,那么kPA·kPB=

简证由已知A(0,−b),B(0,b), 设P(x,y), 则移项整理得:,即kPA·kPB=进一步推广到更一般性结论:

结论3已知A,B是椭圆= 1(a ＞b ＞0)关于原点对称的两个点,P点是椭圆上与A,B两点均不同的点,那么kPA ·kPB=;反之,若kPA ·kPB=,则A,B关于原点对称.

证明设已知A(x0,y0),则B(−x0,−y0),=1,又设P(x,y),则=1,两式相减即kPA · kPB=; 反之, 设A(x0,y0) 关于原点对称的点A′(−x0,−y0), 那么kPA · kPA′=又kPA ·kPB=那么kPA′=kPB, 即P,A′,B三点共线, 由一条直线与椭圆至多有两个交点, 那么A′,B两点重合.

4 应用于高考题求解

有了这样的背景知识, 如果回到开始的高考题中, 我们可以发现, 当点M,N位于y轴两侧时,kAP ·kAQ=kAM ·kAN=由结论3,则P,Q关于原点对称,从而直线l过原点.

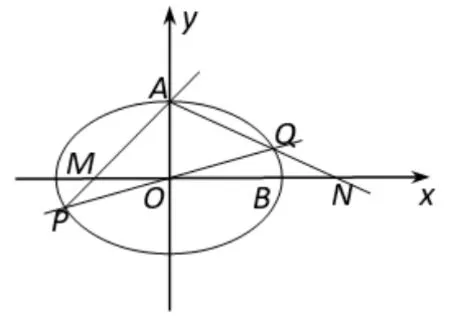
当点M,N位于y轴同侧时, 记点Q关于y轴的对称点为Q′,kAP ·kAQ=kAM ·kAN==−kAP·kAQ′,由结论2 知P,Q′关于原点对称,故P,Q′关于x轴对称,从而直线l斜率不存在.

评注在数学学科核心素养中,“直观想象”是指借助几何直观和空间想象感知事物的形态与变化,利用图形,理解和解决数学问题的素养.结论1,2,3 及其结论3 对于高考题求解的思考,无不渗透着这一素养,特别是通过直观想象发现和提出了问题,并且应用于分析和解决问题.

5 题目进一步变式

通过以上分析,我们对这道高考题已经有了系统的认识,下面给出两道变式,其证明留给读者.

变式1已知椭圆C:= 1 上顶点为A,直线x=m(0＜m ＜2)交椭圆C于点P,Q,直线AP,AQ分别交x轴于点M,N,求证:|OM|·|ON|为定值.(答案: 4)

变式2已知椭圆C:= 1 右焦点为F,点A在椭圆C上, 且AF⊥x轴,M,N为x轴上两点, 且位于直线AF的两侧, 设直线AM,AN分别交椭圆C于P,Q, 若|FM|·|FN|=3,求证: 直线PQ经过定点.(答案: 过原点)

评注高中数学教学要创设合适的教学情境,启发学生思考,引导学生把握数学内容的本质.通过以上分析,今年的这例高考题体现出匠心独运价值,是不可多得的引领我们在教学中注重把握“以数学学科核心素养为导向”的典例.