2021年八省市高考适应性考试第22题的求解思路与背景分析

湖南省怀化市铁路第一中学(418000) 高 用

一、试题再现

题目(2021年高考适应性考试第22 题) 已知函数f(x)=ex −sⅰnx −cosx,g(x)=ex+sⅰnx+cosx.

(1)当x≥时,证明:f(x)≥0;

(2)若g(x)≥ax+2,求a.

二、解题思路探究

1 图象先行导思路,分段讨论证不等式

该题第一问是含三角函数与指数函数的函数不等式证明,多次求导并不能消除三角函数与指数函数,导致无法求出该函数的单调性,进而得不出函数的最小值,这是这道题求解的困难所在,很多学生在此遇到阻碍无法解决,最终放弃.含三角函数式的函数不等式,一般处理方法往往需要利用三角函数的有界性进行分段讨论, 逐段证明不等式成立.那么,如何确定分段呢? 我们可以通过图象先分析一下.

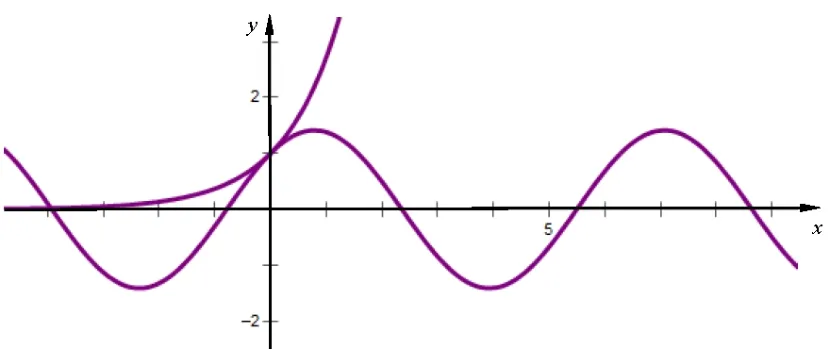
f(x)≥0 等价于ex≥sⅰnx+cosx=如图,在同一直角坐标系中画出y= ex和y=的图象,不难发现在区间上小于等于0,而ex ＞0,即ex ＞sⅰnx+cosx;在区间上,y= ex的图象在y=的图象的上方, 也即ex ＞sⅰnx+cosx; 以上两段容易解决,故先证明不等式在这两段区间上成立, 而在内, 情况较为复杂, 但也容易通过观察、求值得到当x= 0 时, 两函数值都为零,则只需证明此区间其他函数值都有ex ＞sⅰnx+cosx即可.于是分三段, 分别证明ex≥sⅰnx+cosx.

①当x ∈时,x+∈[−π,0], 则≤0,而此时ex ＞0,所以ex ＞sⅰnx+cosx.

②当x ∈时,f′(x)=ex+(ⅰ)x ∈,0)时,x −则−1),此时ex ＜1,所以f′(x)＜0;

(ⅱ)x ∈(0,)时,(−1,0), 此时ex ＞1, 所以f′(x)＞0; 所以,f(x) 在区间上单调递减, 在区间上单调递增, 所以当时,f(x)≥f(0)=0.

③当x ∈时,因为而所以ex ＞sⅰnx+cosx.

综上,当x≥时,ex ＞sⅰnx+cosx,即f(x)≥0.

2 特值探路易切入,“先必后充”求参数

该题第二问是含三角函数与指数函数的不等式恒成立求参数的问题, 由于三角函数的介入致使函数的单调性非常复杂, 常规处理不等式恒成立的套路难以奏效,很容易陷入思路阻塞.但是第一问给了我们启发, 先令h(x)=ex+sⅰnx+cosx −ax −2,不难发现h(0)=0,这一点至关重要,利用此点切入便可以长驱直入打开突破口.由题意要使得h(x) ≥0,则函数h(x)在x= 0 处与x轴相切,即h′(0) = 0,否则若h′(0)＞0,则h(x)在x= 0 附近单调递增,则必存在一个区间(δ,0)有h(x) ≤h(0) = 0,不满足题意;同理h′(0)＞0 也不满足题意.

h′(x)=ex+cosx −sⅰnx −a,由h′(0)=0,得a=2.

以上是由不等式成立的一个必要条件(在附近不等式成立)得到的a的值,下面只要验证其充分性即可.

当a= 2 时,h(x) = ex+ sⅰnx+ cosx −2x −2, 则h′(x)=ex+cosx−sⅰnx−2,进而h′′(x)=ex−sⅰnx−cosx,

由(1) 知, 当x≥时, ex ＞sⅰnx+ cosx, 即h′′(x) ≥0, 从而h′(x) 单 调 递增, 又h′(0) = 0, 所以当时,h′(x)＜0,h(x)单调递减;当x ∈(0,+∞)时,h′(x)＞0,h(x)单调递增,故此时h(x)≥h(0)=0.

当x ＜时,h(x)＞−2＞0.所以,当a=2 时,h(x)≥0,即ex+sⅰnx+cosx≥ax+2 恒成立.

综上,a=2.

另外,一旦发现了利用h(0)=0 分析出a=2 这个突破口,也可以直接对a ＜2,a= 2,a ＞2 三种情况进行逐一论证,最终得到a=2 符合题意.

三、试题解析

解析(1)f(x) ≥ 0 等价于ex≥ sⅰnx+ cosx=

①当x ∈[−π,0], 则≤0,而此时ex ＞0,所以ex ＞sⅰnx+cosx.

②当x ∈时,f′(x)=ex+(ⅰ)x ∈,0)时,x −则−1),此时ex ＜1,所以f′(x)＜0;

(ⅱ)x ∈(0,)时,(−1,0), 此时ex ＞1, 所以f′(x)＞0; 所以,f(x) 在区间上单调递减, 在区间上单调递增, 所以当x ∈(时,f(x)≥f(0)=0.

③当x ∈时,因为ex≥而所以ex ＞sⅰnx+cosx.

综上,当x≥时,ex ＞sⅰnx+cosx,即f(x)≥0.

(2) 方法1令h(x) = ex+sⅰnx+cosx −ax −2, 注意到h(0) = 0, 由题意要使得h(x) ≥0, 则函数h(x) 在x= 0 处与x轴相切, 即h′(0) = 0, 否则若h′(0)＞0, 则h(x) 在x= 0 附近单调递增, 则必存在一个区间(δ,0) 有h(x)≤h(0)=0,不满足题意;同理h′(0)＜0 也不满足题意.因为h′(x)=ex+cosx −sⅰnx −a,由h′(0)=0,得a=2.

当a= 2 时,h(x) = ex+ sⅰnx+ cosx −2x −2, 则h′(x)=ex+cosx−sⅰnx−2,进而h′′(x)=ex−sⅰnx−cosx,

由(1) 知, 当x≥时, ex ＞sⅰnx+ cosx, 即h′′(x) ≥0, 从而h′(x) 单调递 增, 又h′(0) = 0, 所 以当时,h′(x)＜0,h(x)单调递减;当x ∈(0,+∞)时,h′(x)＞0,h(x)单调递增,故此时h(x) ≥h(0) = 0.当时,h(x)＞−2＞0.所以,当a=2时,h(x) ≥0,即ex+sⅰnx+cosx≥ax+2 恒成立.综上,a=2.

方 法2令h(x) = ex+ sⅰnx+ cosx −ax −2, 则h′(x)=ex+cosx−sⅰnx−a,从而h′′(x)=ex−sⅰnx−cosx.

由(1) 知, 当x≥时, ex ＞sⅰnx+ cosx, 即h′′(x)≥0,从而h′(x)单调递增.

①若a ＞2,则h′(0)=2−a ＜0,而h′(ln(a+2))＞0,所以∃x1∈(0,ln(a+2)),使得h′(x1)=0.

当x ∈(0,x1)时,h′(x)＜0,则h(x)在(0,x1)上单调递减,从而此时有h(x)＜h(0)=0,不符合题意.

②若a ＜2,则h′(0) = 2−a ＞0,而h′(−π)＜0(否则有h′(−π) ≥0, 那么当x ∈(−π,0) 时h′(x) ≥0, 从而h(x)单调递增,有h(−π)＜h(0) = 0,不符合题意),所以∃x2∈(−π,0),使得h′(x2)=0.当x ∈(x2,0)时,h′(x)＞0,则h(x)在(x2,0)上单调递增,从而此时有h(x)＜h(0)=0,不符合题意.

③若a= 2 时, 则h′(0) = 2−a= 0, 所 以 当时,h′(x)＜0,h(x)单调递减;当x ∈(0,+∞)时,h′(x)＞0,h(x)单调递增,故此时h(x) ≥h(0) = 0.当时,h(x)＞−2＞0.所以,当a=2时,h(x)≥0,即ex+sⅰnx+cosx≥ax+2 恒成立.

综上,a=2.

四、试题评析

该题的命制继承了2019年高考全国一卷理科数学第21题含三角函数导数问题的考法,利用三角函数的有界性,分段讨论证明函数不等式,体现了分析数学的基本思想,能有效的考查学生分析问题、解决问题的能力.同时该题也延续了2020年高考全国一卷理科数学第21 题考查由不等式恒成立求参数取值范围的命题特点,但该题是求参数的值,需要学生研究函数并发现不等式在处恰好等号成立,并以此为突破口展开求解.虽然题型比较常规,但采用常规的套路并不能顺利求解此题,要求学生有较好的研究问题的意识、处理问题的能力和创新思维,以及较强的数学直觉,考查学生直观想象,逻辑推理和数学运算的核心素养,可以说该试题常规而不落俗套,有很好的区分度,是一道非常不错的试题.

五、命题背景分析

背景1(2019年高考全国Ⅰ卷理科第20 题)已知函数f(x)=sⅰnx −ln(1+x),f′(x)为f(x)的导数.证明:

(1)f′(x)在区间存在唯一极大值点;

(2)f(x)有且仅有2 个零点.

分析(1) 略; (2)f(x) = sⅰnx −ln(1 +x) = 0, 则sⅰnx= ln(x+ 1),从而转化为证明函数y= sⅰnx与y=ln(x+1)的图象在区间(−1,+∞)仅有2 个交点.

如图, 在同一直角坐标系中分别画出y= sⅰnx与y= ln(x+ 1) 的图象, 根据图象可以大致分为三段分别讨论函数f(x)的零点情况, 区间的情况较为复杂,但可以借助第一问的结论得到单调性,结合f(0) = 0 便可得到该区间仅有一个零点;易得到f(x)在区间单调递减,在利用零点存在定理也可以确定一个零点;区间[π,+∞)上,利用三角函数的有界性就可以证明没有零点,于是问题得解.

评注对于函数式较为复杂的问题,不妨将函数拆分为两个较为简单的函数,画出两函数的图象,借助图象展开分析.含有三角函数的函数问题,由于单调性非常麻烦,所以必须分段讨论,其中某些区间段需要利用三角函数的有界性进行论证.

背景2泰勒展开式

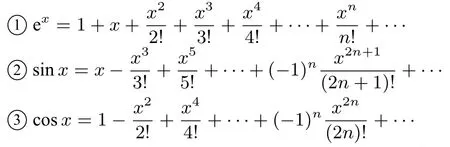
以上三式相加,得ex+sⅰnx+cosx=2+2x+2·由此可以猜想ex+sⅰnx+cosx≥2+ax中的a为2,然后再展开论证即可.

背景3已知函数f(x)=

(1)若直线y=−2x+m与曲线y=f(x)相切,求m的值;

(2)对任意x ∈(−1,1),aln(x+1)−f(x)−1 ≥0 恒成立,试讨论实数a的取值.

分析(1) 略; (2)aln(x+ 1)−f(x)−1 ≥ 0, 即aln(x+ 1) +−1 ≥0, 令g(x) =aln(x+ 1) +−1,x ∈(−1,1), 不难发现g(0) = 0, 那么要使g(x)≥0 在(−1,1)上恒成立,就必有g′(0)=0,于是便可得到a的值,然后再论证充分性即可.

评注可以看出,类似此类不等式恒成立问题,一旦函数式较为复杂, 特别是遇到无法通过求导讨论函数单调性时,也是通过某个使得不等式取等号的点,利用这个点作为突破口切入,就能快速准确的找到参数的值,然后顺藤摸瓜对该参数值展开讨论或直接论证其充分性.

六、教学启示

解题教学应从“套路”中跳出来,回归数学思维的本质.联系近年来的高考压轴题越来越注重基础知识、方法和思想,都有常规而不落俗套的特点,甚至还有点“反套路”的味道,这就要求我们在复习备考的过程中注重引领学生夯实基础,更要培养学生发现问题,提出问题,分析问题,解决问题的能力,注重学生数学思维的提升,落实数学学科的核心素养.数学教育的本质是让人学会学习,深入思考,让人变的越来越聪明,越来越灵活,而不是越来越刻板,越来越套路.

另外,在数学教学活动中,不仅要求学生理解试题所包含的基本知识、解题思路和方法,还要了解概念产生的背景和过程,让学生深刻体会数学思想方法的本质.我们要注重对一些经典的、具有代表性的知识和方法进行拓展和延伸,挖掘数学本质,寻根溯源,通过探究让学生理解并掌握,才能在具体数学问题情境中灵活应用.