题在书外 根在书中——2020年新高考全国卷Ⅱ第21题的探析

广东省佛山市乐从中学(528315) 林国红

“年年岁岁花相似,岁岁年年题不同”.每年都有不少的优质高考试题,这些试题是命题专家精心设计的杰作,对中学教学有良好的导向性,值得我们去品味与探析.要充分认识高考题所蕴含的价值,挖掘高考题的功能,发挥其内在作用,并以此来促进教学.

下面笔者以2020年新高考全国卷Ⅱ(海南卷)第21 题为例,进行详细分析与解答,追本溯源,说明立足教材,重视课本例习题的重要性,并给出相应的变式练习,供大家参考,希望能抛砖引玉.

一、题目呈现与分析

题目(2020年新高考全国卷Ⅱ(海南卷)第21 题)已知椭圆C:= 1(a ＞b ＞0)过点M(2,3),点A为其左顶点,且AM的斜率为

(1)求C的方程;

(2)点N为椭圆上任意一点,求ΔAMN的面积的最大值.

立意分析题目结构清晰,知识方面主要考查直线方程,椭圆方程,直线与椭圆的位置关系,点到直线的距离公式,三角形的面积,圆锥曲线上的点到直线距离的最大值等;思想方面主要考查转化与化归,数形结合等思想.综合考查考生逻辑思维、推理论证及运算求解等方面的能力,试题的思维过程和运算过程体现了能力立意的思想,较好地体现了解析几何中核心内容和基本思想方法的考查.

由于问题(1)较为简单,本文不作讨论,下面从不同视角,对问题(2)进行解答与探究.

二、多视角思考,解法探析

分析由(1) 可得椭圆C的方程为直线AM的方程为x −2y+ 4 = 0, 且|AM|=设点N到直线AM的距离为d, 则ΔAMN的面积为所以问题(2) 转化为: 求椭圆上的点N到直线AM距离的最大值.

解法1(数形结合法)如图1 所示,当直线l平行于直线AM(且与AM距离较远的一条),与椭圆C相切于点为N,此时ΔAMN的面积取得最大值.设直线l的方程为x −2y+m= 0, 联立化简得16y2+12my+3m2−48=0,因为直线l与椭圆C相切,于是

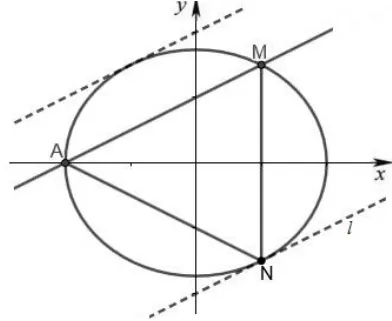
图1

Δ=144m2−4×16(3m2−48)=0,解得m=±8,所以直线l的方程为x −2y −8=0.点N到直线AM的距离即两平行线之间的距离,利用平行线之间的距离公式可得:所以ΔAMN的面积的最大值S=

解法2(导数法)如图1,设切点N(x0,y0)(x0＞0,y0＜0),则得y=于 是y′=从而直线l的斜率为k=因为l//AM, 所以解得x0= 2, 从而y0=−3, 所以N(2,−3).故点N到直线AM的距离d=所以ΔAMN的面积的最大值S=

解法3(椭圆的切线方程)设切点N(x0,y0)(x0＞0,y0＜0),则=1,因为直线l是椭圆C的切线,所以直线l的方程为=1,即3x0x+4y0y−48=0.又因为l//AM,从而即3x0=−2y0.联立解得x0=2,y0=−3,所以N(2,−3).故点N到直线AM的距离d=所以ΔAMN的面积的最大值

解法4(参数方程法)由于椭圆C的方程为= 1, 且点N在椭圆C上, 可设θ ∈[−π,π].则点N到直线AM的距离d=从而当即θ=时,d取得最大值此时N(2,−3).所以ΔAMN的面积的最大值S=18.

解法5(判别式法)设N(x,y), 则点N到直线AM:x −2y+4 = 0 的距离d=因此问题转化为求x −2y的最值问题.设t=x −2y,则y=联立化简得4x2−2tx+t2−48=0,因为关于x的一元二次方程有实数根,于是Δ = (−2t)2−4×4(t2−48) ≥0,解得−8 ≤t≤8.从而当t= 8,即x −2y= 8 时,距离d最大,最大值为d=所以ΔAMN的面积的最大值S==18.

解法6(向量法)设N(x,y)(x ＞0,y ＜0),则点N到直线AM:x −2y+4=0 的距离d=因此问题转化为求x −2y的最值问题.

构造向量m=,n=则|m|== 1,|n|== 8,m · n=x −2y.由向量的性质|m·n|≤|m|×|n|, 所以有|x −2y|≤8,即−8 ≤x −2y≤8, 当且仅当即y=时, 等号成立, 联立解得x= 2,y=−3.从而当x= 2,y=−3,即x −2y= 8 时,距离d最大,最大值为d=所以ΔAMN的面积的最大值S=

解法7(柯西不等式)设N(x,y)(x ＞0,y ＜0), 则点N到直线AM:x −2y+4 = 0 的距离d=因此问题转化为求x −2y的最值问题.于是(x −2y)2=当且仅当即y=时, 等号成立,联立从而有−8 ≤x −2y≤8, 即x −2y= 8 时, 距离d最大, 最大值为d=所以ΔAMN的面积的最大值

评注问题(2)要解决点到直线距离的最值问题,解答中分别使用解析几何、方程、导数、三角、向量、函数、不等式等高中核心知识进行解决,体现了知识的横向联系.因此要对典型高考题要深入挖掘,探求试题背后的思想方法,注重一题多解,力求对所学的知识融会贯通.

从不同的思维角度分析同一道题目,得到不同的解题方法,一题多解的方式增加了题目涉及的知识广度,以一带多,减少了考查同样多的知识所需的题量.从数学知识的角度来看,通过解题发现知识的相互联系,体会知识之间的转化过程,从多角度地思考和发现问题,构建知识网络体系.这样,在学习基础知识、掌握基本技能的同时,能培养学生思维的广阔性、深刻性、灵活性以及创新性,能够使学生对学习的内容有一个整体的认识,并将知识融会贯通,举一反三,开阔眼界,活跃思维,从而提炼出数学思想与方法,这正是数学教学的核心.

三、追本溯源

问“题”那得清如许,唯有源头活水来,可以看出今年考题的问题(2)的“母题”来源于教材的上述例题,只是将例题进行适当的改编而已.立足教材,选编教材原题,生成教材变题,是高考命题的一个不争的事实,这体现了高考命题的公平性和基础性原则.所以教师要善于钻研教材,用“慧眼”去发现有典型性、可拓展性的例题或习题,善于作解后反思,方法的归类,规律的总结与技巧的揣摩,再进一步对例习题进行挖掘、拓展、引申,扩大例习题的辐射面,以此提高复习的效率.

四、试题的变式

为了加强学生对某一类问题的掌握,适当地对题目加以改编再练习,会起到强化解题思想方法的积极作用,通过“一题多变”,能够加深思维深度,学会由表及里,让学生在亲身实践中寻求变通,悟出其中问题的本质,从而为今后的解题迁移找到共同的固着点,对于形成完善的数学思维结构和发展数学思维能力具有重要意义.对于本考题的问题(2),可以进行如下变式训练:

1.变曲线: (2006年高考全国卷1 理科第8 题) 抛物线y=−x2上的点到直线4x+3−8=0 距离的最小值是( )

2.变直线: (2008年高考江苏卷第21 题)在平面直角坐标xOy中,点P(x,y)是椭圆+y2=1 上的一个动点,求S=x+y的最大值.

3.变求最值为求直线: (2017年高考全国卷1文/理科第22 题) 在直角坐标xOy中, 曲线C的参数方程为(θ为参数), 直线l的参数方程为(t为参数).

(1)若a=−1,求C与l的交点坐标;

(2)若C上的点到l距离的最大值为求a.

4.变求最大值为求最小值: (2019年高考数学全国卷Ⅰ文/理科第22 题) 在直角坐标系xOy中, 曲线C的参数方程为(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系, 直线l的极坐标方程为

(1)求C和l的直角坐标方程;

(2)求C上的点到l距离的最小值.

五、链接高考

圆锥曲线上的点到直线距离相关类型的考题是高考中的重要考点,倍受命题者青睐.为了突显考题的有迹可循,把握复习的侧重点,提高复习效率,下面给出部分相关的高考试题,以供参考.

1.(2019年高考江苏卷第10 题)在平面直角坐标系xOy中,P是曲线y=x+(x ＞0)上的一个动点,则点P到直线x+y=0 的距离的最小值是____.

2.(2014年高考全国卷1 理科第23 题) 已知曲线直线(t为参数).

(1)写出曲线C的参数方程,直线l的普通方程;

(2)过曲线C上任一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.

3.(2011年高考褔建卷理科第21(2)题)在直角坐标系xOy中,直线l的方程为x −y+4 = 0,曲线C的参数方程为(α为参数).

(1)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为判断点P与直线l的位置关系;

(2)设点Q是曲线C上的一个动点,求它到直线的距离的最小值.

高考试题是精心之作,每年的高考题在命题角度、题型、难度等方面都进行了充分考虑,是知识、能力和思想方法的载体,是命题思想、命题理念的程序化展现,具有典型性、示范性和权威性.除了具有测试与选拔功能外,还具有良好的教学功能,要了解高考动向、把握高考脉搏,高考试题的研究分析是重要的路径.可以看出今年考题的问题(2)与上述展示的高考题(含“变式练习”)是同类题,这说明命题专家很重视命题的传承和相互借鉴.所以在高考的备考中,适当加入高考真题的训练的必要的,特别是近几年的高考真题.

六、结束语

罗增儒教授语: 教材是课程的载体,因此高考命题最具体、最方便的依据其实是教材.数学高考试题有“源于教材,高于教材”的特点,但万变不离其宗,“宗”就是教材,即是“题在书外,根在书中”.苏联数学教育家奥加涅曾说“很多习题潜在着进一步扩展其教学功能、发展功能和教育功能的可能性……”,教材中的例习题是经过编者精心设计的,具有典型性的范例作用,大多都蕴含着深刻的背景、丰富的数学思想,很多高考题是教材例题、习题的组合、加工、引申、拓展和类比,这充分体现教材是高考试题之根所在.因此,高三的数学复习应立足于教材,钻研教材,深刻领悟教材中数学知识的作用和蕴含的人文素养的文化价值;活用教材,对教材中有潜在本质规律的材料、例题、习题进行归纳、类比、拓展,充分挖掘,将其价值发挥出来,从而实现教材教学功能的最大化、最优化.