2021年八省市高考适应性考试第7题的解法探究与推广
2021-04-21广东省湛江市二中海东中学524057高海秀
广东省湛江市二中海东中学(524057) 高海秀
广东省湛江市一中培才学校(524037) 魏 欣
一、经典试题展示
试题(2021年适应性测试(八省市联考)数学试题第7题)已知抛物线y2=2px上三点A(2,2),B,C,直线AB,AC是圆N:(x −2)2+y2=1 的两条切线,则直线BC的方程为( )
A.x+2y+1=0 B.3x+6y+4=0
C.2x+6y+3=0 D.x+3y+2=0
二、多角度的解法探究
方法一(一般算法) 如图1 所示, 因为A(2,2) 在抛物线y2= 2px上, 故22= 2p ×2,即p= 1.所以抛物线为y2= 2x.设过点A(2,2) 与圆(x −2)2+y2= 1 相切的直线的方程为:y −2 =k(x −2),即kx −y+ 2−2k= 0.则圆心(2,0) 到切线的距离=1,解得
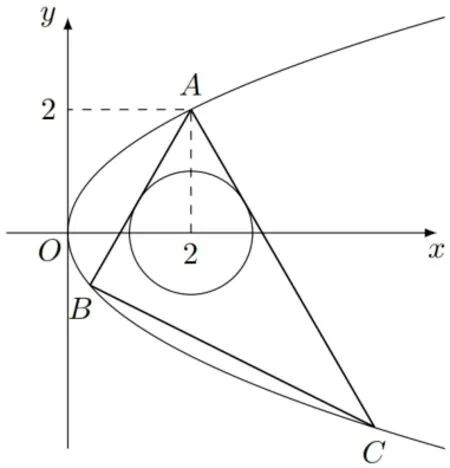
图1
直线AB的方程为:y −2 =直线AC的方程为:联立得=0,故xA·xB=由xA= 2 得xB=联立得0.故由xA=2 得xC=故yC=故yB+yC=−4.由B,C在抛物线上, 可知直线B,C的斜率为kBC=故直线B,C的方程为y −即直线B,C的方程为3x+6y+4=0.
方法二(利用垂径定理与抛物线弦方程)
首先我们回顾两个已知结论.
1.垂径定理: 设A、B是抛物线y2=2px上的两点,AB中点是N,则

2.抛物线两点弦方程: 设A、B是抛物线y2=2px上的两点,则

并且
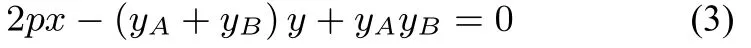
由(1) 式得:同理得:−2, 于是yB+yC=−4,yByC=代入(3) 式得直线BC的方程为3x+6y+4=0.
方法三(设点法) 由(3) 式得: 直线AB的方程为2x −(2+yB)y+2yB=0.由于AB与圆(x −2)2+y2=1相切,所以=1.化简得:0.同理:+ 12yC+ 8 = 0.于是,yB,yC是方程3y2+ 12y+ 8 = 0 的两根, 所以代入(3)式得直线BC的方程为3x+6y+4=0.
方法三改进由(3) 式得: 直线AB的方程为2x −(2+yB)y+2yB= 0.由于AB与圆(x −2)2+y2= 1 相切,所以=1.化简得:+12yB+8=0.即6xB+ 12yB+ 8 = 0⇒3xB+ 6yB+ 4 = 0, 同理:3xC+6yC+4=0,所以直线BC的方程为3x+6y+4=0.
方法四(曲线系)直线AB的方程为:y−2=直线AC的方程为:y −2 =所以B,C满足:所 以(y+2)23y2+ 12y+ 8 = 0, 将y2= 2x代入上式得: 直线BC的方程为3x+6y+4=0.
方法五(直线参数方程法) 设直线AB的参数式方程为联立抛物线方程y2= 2x, 消去x,y得:所 以同理可得:所以kBC=所以直线BC的方程为3x+6y+4=0.
方法六(抛物线参数方程法) 利用抛物线的参数 方 程, 设所以所以同理可得:所以kBC=所以直线BC的方程为3x+6y+4=0.
方法七(张角定理法)
张角定理: 如图2, ΔABC,AD交BC与D,则(用面积法很容易证明)
设直线AB的参数式方程为
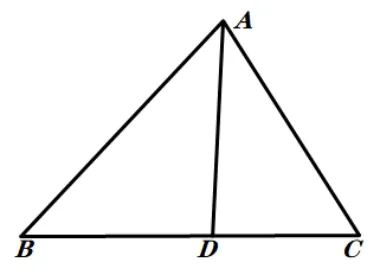
图2
联立抛物线方程y2= 2x, 消去x,y得:=0,所以设直线AC的参数式方程为联立抛物线方程y2=2x,消去x,y得:由张角定理得:所以将E点坐标代入选项,B 正确,故选B.
方法八(利用切线斜率的相反数得结论) 首先证明如下命题: 已知抛物线C:y2= 2px,定点A(a,b)∈C,动点P(x1,y1)∈C,Q(x2,y2)∈C,kAP+kAQ= 0.则kPQ为定值,且等于抛物线在A点处切线斜率的相反数.
实际上,= 2px1= 2px2,b2= 2pa,kPQ=所以kAP=kAP+kAQ= 0, 所以2p(y1+y2+2b) = 0, 所以y1+y2=−2b,kPQ=为定值.因此,命题成立.
B点坐标求法同上, 得下面用上述定理求直线BC的斜率.对y2= 2x两边对x导得:2yy′= 2, 所以所以直线BC的方程为3x+6y+4=0.
三、变式训练
变式(2020年厦门模拟节选) 如图3 所 示, 已知A,B,C是拋物线y=x2上相异的三 点,如果直线AB、AC与圆x2+ (y −2)2= 1 相切,求证: 直线BC也与圆N相切.
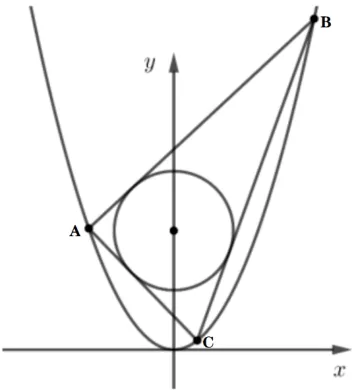
图3
证明设A(a,a2),B(b,b2),C(c,c2), 则直线AB:
y −a2=(x −a).所以(a+b)x −y −ab= 0.因为AB与圆相切,所以所以
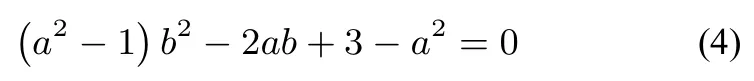
同理:
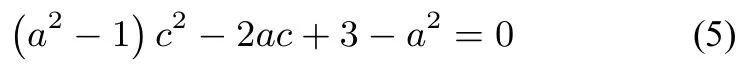
由(4),(5)式知:b,c是方程(a2−1)x2−2ax+3−a2= 0的两根.所以所以直线BC的方程 为: (b+c)x −y −bc= 0, 因 为所以直线BC也与圆N相切.
四、性质推广
(一)抛物线在斜率和(或积)为定值条件下的性质
定理1已知抛物线C:y2=2px,定点A(a,b)∈C,动点P(x1,y1)∈C,Q(x2,y2)∈C,若kAP+kAQ=γ,
(Ⅰ)当γ= 0 时,kPQ为定值,且等于抛物线在A点处切线斜率的相反数;
(ⅠⅠ) 当γ /= 0 时, 则直线PQ恒过定点D, 且
证明= 2px1= 2px2,b2= 2pa,kPQ=
(Ⅰ) 若kAP+kAQ= 0, 所以2p(y1+y2+2b) = 0, 所以y1+y2=−2b,kPQ=为定值, 2yy′= 2p, 所以
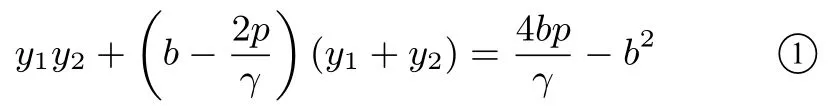
直线PQ:y −y1=(x −x1),所以
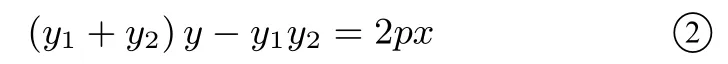
①+ ②得(y1+y2)所以直线PQ过定点
定理2已知抛物线C:y2= 2px,定点A(x0,y0)∈C,动点P(x1,y1)∈C,Q(x2,y2)∈C,若kAP ·kAQ=γ,则直线PQ恒过定点D,且
证明联立消x, 得y2−2pmy −2pn= 0,y1+y2= 2pm,y1y2=−2pn,x1+x2=m(y1+y2) + 2n= 2pm2+ 2n,x1x2=(my1+n)(my2+n) =m2y1y2+mn(y1+y2) +n2=n2, 由得y1y2−y0(y1+y2) +=γx1x2−x0(x1+x2)+,−2pn −2pmy0+=所以γn2+(2p −2γx0)n −解得
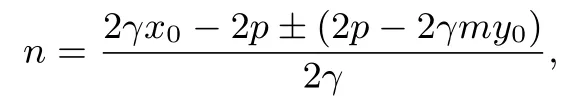
n1=x0−my0(舍),n2=x0+my0−,所以直线PQ方程x −x0+=m(y+y0),恒过
(二)双曲线在斜率和(或积)为定值条件下的性质
定理3已知双曲线=1,(a >0,b >0),定点A(x0,y0)∈C(点A不是双曲线顶点),动点P(x1,y1)∈C,Q(x2,y2)∈C,若kAP+kAQ=γ,
(Ⅰ)当γ=0 时,kPQ=为定值,且等于双曲线在A点处切线斜率的相反数;
(ⅠⅠ) 当γ /= 0 时, 则直线PQ恒过定点D, 且
证明设PQ方程x=my+n, 即x −x0=m(y −y0)+my0+n−x0,所以将b2[(x −x0)+x0]2−a2[(y −y0)+y0]2−a2b2=0,展开得
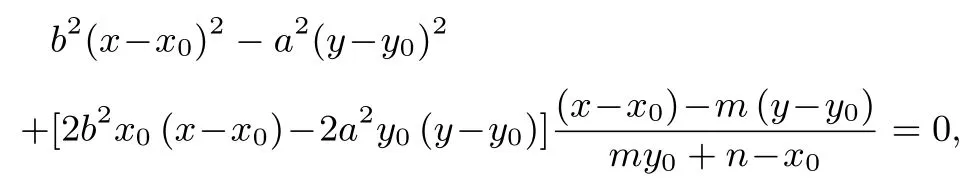
整理得到
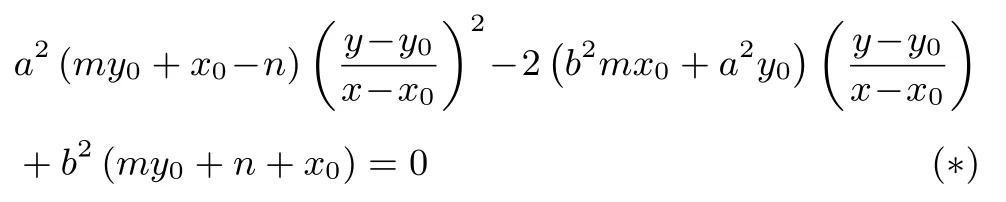
(Ⅰ) 当γ= 0 时,kPQ=为定值.把= 1, 的两边对x求导,= 0, 在A处的导数y′=
(ⅠⅠ) 当γ /= 0 时,γa2n=γa2(my0+x0)−2(b2x0m+a2y0), 所以n=my0−直线恒过
定理4已知双曲线= 1,(a >0,b >0),定点A(x0,y0)∈C,动点P(x1,y1)∈C,Q(x2,y2)∈C,若kAP ·kAQ=γ,
(Ⅰ)当γ=时,kPQ=为定值;
(ⅠⅠ)当γ /=时,则直线PQ恒过定点D,且
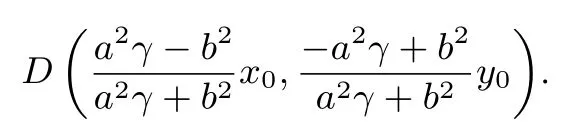
证明由(∗)得到
(Ⅰ)当γ=时,my0=−x0,kPQ=为定值.
(三)椭圆在斜率和(或积)为定值条件下的性质
定理5已知椭圆= 1,(a >b >0) 定点A(x0,y0)∈C, (点A不是椭圆顶点), 动点P(x1,y1)∈C,Q(x2,y2)∈C,若kAP+kAQ=γ,
(Ⅰ)当γ= 0 时,kPQ=为定值,且等于椭圆在A点处切线斜率的相反数;
(ⅠⅠ) 当γ /= 0 时,则直线PQ恒过定点D, 且
定理6已知椭圆= 1,(a >b >0) 定点A(x0,y0)∈C(点A不是椭圆顶点), 动点P(x1,y1)∈C,Q(x2,y2)∈C„若kAP ·kAQ=γ,
(Ⅰ)当γ=时,kPQ=为定值;
(ⅠⅠ) 当γ /=时,则直线PQ恒过定点D, 且
定理5,定理6 的证明见文[1].
应用以上定理,可以很容易解决如下两题.
1.(高二第26 届“希望杯”赛第20 题) 已知抛物线C:y2= 4x,A(4,4), 动点P(x1,y1)∈C,Q(x2,y2)∈C,若kAP+kAQ=则直线PQ过定点D,点D的坐标是____.
2.(2009年高考辽宁卷理科第20 题文科第22 题)已知,椭圆C经过一点A(1,1.5),两个焦点为(−1,0),(1,0).
(1)求椭圆C的方程.
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
