CH4在PVDF中渗透行为及机理的分子模拟研究
2021-04-20张学敏李厚补肖春红冯金茂钟明强
张学敏,王 品,李厚补,周 腾,肖春红,冯金茂,钟明强
(1. 长安大学材料科学与工程学院,西安710064;2. 浙江伟星新型建材股份有限公司,浙江临海317000;3. 中国石油集团石油管工程技术研究院石油管材及装备材料服役行为与结构安全国家重点实验室,西安710077;4. 浙江工业大学材料科学与工程学院,杭州310014)
0 前言
酸性天然气集输用钢质管道在使用过程中易出现腐蚀、穿孔及泄露等现象,严重影响油气的开采效益,并存在巨大的安全隐患[1]。近年来,具有优异的柔韧性、耐腐蚀性以及抗疲劳性的增强热塑性塑料复合管正在成为含硫油气输送的理想管材。这类管材是以热塑性塑料管为内衬层,以金属或非金属材料作为增强层,外敷热塑性塑料保护层复合而成。其中,PVDF 因具有优异的耐高温、耐化学腐蚀以及高阻隔性成为陆地及海洋用增强热塑性塑料复合管内衬层材料的良好选择[2]。Shamsuddoha 和Scheichl 等[3-4]发现气体分子的自由运动会在热塑性塑料表面产生吸附、扩散等渗透现象,这不仅会导致内衬材料起泡失效,吸附在热塑性塑料内的气体还会沿内衬厚度方向发生扩散,进入内衬层和增强层之间的环空,进而导致内衬层坍塌失效或腐蚀金属增强层,使得管线使用寿命大幅降低。因此,研究及确定气体分子在热塑性塑料中的渗透行为和机理对于高阻隔热塑性塑料内衬材料选材及气体渗透过程预防具有重要指导意义。
目前,对小分子气体在热塑性塑料中的渗透行为研究大多采用质量法、浓度法、压力法、体积法等实验方法[5-11]。Novak 等[5]基于重量法,釆用磁悬浮天平测量了乙烯气相聚合条件下乙烯/1-己烯在低密度聚乙烯内的渗透系数。WANG 等[6]和WANG 等[7]采用动态浓度法测量了异戊烷和己烷在聚乙烯中的吸附溶解量,并通过气相色谱-氢火焰离子检测器检测出口气相浓度的变化,并以此判断平衡与否,进而得到异戊烷和己烷在聚乙烯中的渗透系数。Sato 等[8-10]先后采用压力法测量了高温高压下CO2和N2在熔融态聚乙烯、聚丙烯和聚苯乙烯的渗透系数。Mckenn 等[11]釆用体积法研究了乙烯/丁烯在聚乙烯中的渗透系数。但以上通过实验法获得气体分子在聚合物中的渗透系数不仅耗费实验时间和资源,而且不能从分子理论上解释渗透机理。分子模拟是以计算机为辅助工具在原子水平上对晶体结构行为进行模拟的手段,可从原子角度揭示气体分子在聚合物中的运动轨迹及渗透行为,能较好地弥补实验条件方面的不足。陶长贵[12]等运用分子模拟对不同温度下O2在聚丙烯内的渗透行为及扩散机理进行了研究,模拟结果表明随温度的升高,O2在聚丙烯中的溶解系数减小而扩散系数增大,O2在聚丙烯内是以空穴形式存在的自由体积之间扩散。钟颖[13]运用分子模拟的方法研究了CH4在聚叔丁基乙炔中渗透行为,发现CH4在聚叔丁基乙炔中的渗透系数与实验值基本吻合,运动轨迹大部分时间都在空穴内运动,只有当孔与孔之间的临时通道足以其通过时,才能进行一次成功的跳跃。岳雅娟[14]用分子模拟方法研究了有机分子在聚乙烯膜中的渗透过程,结果表明在同种膜的渗透过程中,渗透的大小取决于有机分子对膜的溶解的大小。尽管目前关于小分子气体在聚合物中渗透行为及机理的研究已经很多,但对于天然气中的典型气体CH4在PVDF 中的渗透行为及机理尚未有合理的解释和研究。因此,本文基于分子模拟方法系统研究了不同压力和温度下油气环境中的典型气体CH4在PVDF 材料中的渗透行为,分析了温度及压力对气体渗透能力的影响,并结合CH4在PVDF 中的吸附位点及扩散轨迹,从原子角度探讨了其渗透机理,为油气介质在热塑性塑料中的渗透性评价及控制提供支撑。
1 模型构建和模拟参数设置
1.1 初始结构建立
首先,利用Material stutio7.0 中的Visualizer 模块构建CH4分子[图1(a)]和偏氟乙烯(VDF)单体[图1(b)];其次,利用Amorphous 模块构建三维周期边界条件下的PVDF 晶胞模型用于吸附过程模拟,该晶胞模型由含有4 条聚合度为10 的PVDF 链组成[图1(c)];然后,构建用于扩散过程模拟的CH4/PVDF 混合晶胞模型,该模型中含有4个CH4分子和4条聚合度为10的PVDF 链[图1(d)]。在该混合模型体系中,CH4分子与PVDF 分子链间存在范德华作用力,当溶解行为发生时,CH4分子通过范德华力的作用吸附在PVDF 链内,范德华作用力越强,吸附能力也越强,越易吸附[15];当扩散行为发生时,CH4分子与PVDF 分子链间之间的范德华力越强,则其为了克服周围PVDF 分子链对它的束缚力而跳跃到其他空穴所需的能量会更大,扩散过程越不易进行。

图1 气体分子及晶胞结构模型Fig.1 Gas molecule and cell structural model
1.2 吸附模拟过程及参数设置
CH4分子在PVDF 中的吸附模拟方法采用Monte Carlo 统计方法。分别研究压力2.5 MPa 时不同温度(30、40、60 和80 ℃)下的吸附行为,以及30 ℃时不同压力(2.5、6.4、8.5 和10 MPa)下的吸附行为。首先对图1(a)中构建的CH4分子模型使用Smart Minimizer 模块进行能量最小化处理;其次对图1(c)中构建的PVDF 晶胞模型进行能量最小化处理和200 ps的NPT和NVT 系综优化以降低模拟晶胞构建过程中不稳定结构带来的影响,使晶胞达到松弛得到最终的稳定构型;最后启动Sorption模块以能量最小化后的CH4分子为吸附质,系综优化后的PVDF 晶胞稳定模型为吸附剂,模拟CH4分子在PVDF 中的吸附行为,得到不同条件下CH4分子在PVDF 中的吸附热和溶解系数。整个模拟过程力场采用COMPASS,方法为Metropolis,电子势和范德华势分别采用Ewald 和Group Based 方法进行统计处理,其中平衡步数为1×105步,生产步数为1×106步。
1.3 扩散模拟过程及参数设置
CH4分子在PVDF 中的扩散模拟方法采用分子动力学法,扩散温度及压力与1.2 中设定的吸附参数相同。首先对图1(d)中构建的CH4/PVDF混合晶胞模型使用Smart Minimizer模块进行能量最小化处理,初始晶胞密度设为1.76 g/cm3;其次再进行1 000 ps的NPT和NVT动力学优化,使晶胞足够松弛,得到稳定构型的扩散晶胞模型;最后利用Forcite模块分析原子轨迹获得均方位移(Mean Square Displacement,MSD),进一步计算出气体分子的扩散系数和渗透系数。模拟过程在周期性条件下进行,采用COMPASS力场计算相互作用,温度及压力采用Andersen-Berendsen控温控压方法,起始速度采用Maxwell-Boltzmann 随机分布,模拟步长为1.0 fs,每1 000步记录一次体系的轨迹信息。
2 模拟结果与讨论
2.1 CH4在PVDF中的渗透行为
气体在聚合物中的渗透性通常由2 个因素决定[16]:一是气体在聚合物中的溶解能力;二是气体在聚合物中的扩散能力。因此,气体的渗透系数通常表示为溶解系数和扩散系数的乘积,如式(1)所示:

式中 P——渗透系数,cm3(STP)·cm/cm2·s·Pa,代表了气体通过聚合物的难易程度
D——扩散系数,cm2/s-1,反映了渗透分子与聚合物体系的动力学特性
S——溶解系数,cm3(STP)/cm3·Pa,反映了渗透分子与聚合物相互作用的热力学特性
溶解系数S 描述了处于平衡状态下的气体在聚合物中的浓度C 和压力Pi的关系。用Dual Mode 模型[17-18]可以表示为:

式中 KD——亨利常数
CH——Langmuir吸附容量
b——Langmuir常数
C——气体在聚合物中的浓度,cm3(STP)/cm3
Pi——气体在聚合物中的压力,Pa
为求解分子气体在聚合物中的溶解系数S,常采用吸附等温线法。吸附等温线法是在一定的压力范围内进行一系列的巨正则蒙特卡洛(GCMC)模拟,可通过Sorption 模块里面的Calculation-Adsorption isotherm 选项计算吸附等温线,并由此分析气体小分子在PVDF里面的吸附溶解,得到渗透分子的浓度C 随着压力Pi变化的曲线,通过求出压力为零时的极限斜率,从而得到溶解系数[19],即:

扩散系数D 在扩散过程的研究中常被用来描述传质、传热等过程。扩散系数由Fick第一定律定义[20]:

式中 Ji——第i物质颗粒的通量
ai——i物质的活度,通常假定活度等于浓度
Fick 第一定律的实现条件是等温等压。微观上扩散系数同粒子速度的自相关函数有关。
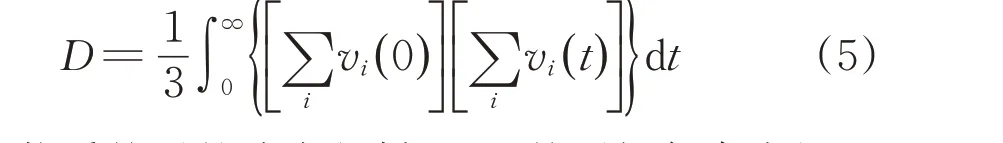
若i物质粒子的浓度很低,而且粒子间仅存在短程作用力,则式(5)可简化成:

从上式(6)可以得到,扩散系数即为粒子的速度自相关函数的时间积分。如果时间无限长,则式(6)可写成如下形式:

式中 Na——a物质的粒子数
r(t)——t时刻粒子的坐标
r(0)——初始坐标
[ri(t)-ri(0)]2——分子的均方位移MSD 的系综平均
式(7)即为爱因斯坦方程(Einstein equation)[21-22]。爱因斯坦方程假设扩散是粒子跳跃式的跃迁,这种跃迁称为正常规则扩散。在这种前提下,Da和MSD 成线性关系。由于MSD 的值已对扩散原子数Na进行了平均,取m 为分子模拟得到的均方位移曲线的斜率,上式(7)则可简化为:

2.1.1 模型可靠性验证
为验证分子模拟气体渗透行为结果的准确性和可靠性,将模拟获得的渗透系数与实验值进行比较。实验方法如下:采用VAC-V2 型压差法气体渗透仪测量气体的渗透系数,试样为厚度350 μm 的PVDF 薄片,在试样两侧压差为0.1 MPa 的条件下检测气体渗透通过薄膜引起低压侧压力的变化量,并根据式(9)计算得到气体的渗透量Q,气体渗透系数P由式(10)得出。
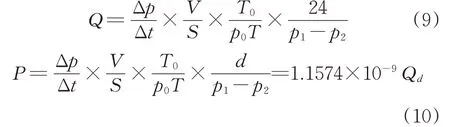
式中 Q——材料的气体渗透量,cm3/m2·d·Pa
Δp/Δt——稳定透过时,单位时间内低压室气体压力变化的算术平均值,Pa/h
V——低压室体积,cm3
S——试样的试验面积,m2
T——试验温度,K
p1-p2——试样两侧的压差,Pa
T0、p0——标准状态下的温度(274.15 K)、压力(1.013 3×105Pa)
d——试样厚度,cm
Qd——气体通过厚度为d 的试样的的气体渗透量,cm3/m2·d·Pa
由以上实验获得室温下(30 ℃)CH4在PVDF 中的渗透系数为0.106×10-11cm3(STP)·cm·cm2/s·Pa。
由于实验压差为0.1 MPa,为保证参数的一致性,在以上模型构建的基础上,设定压力为0.1 MPa,温度为30 ℃的渗透条件进行模拟,其吸附等温线和均方位移曲线如图2 所示,据此计算出的模拟渗透系数为0.158×10-11cm3(STP)·cm/cm2·s·Pa。对比实验值和模拟值可以看出,两者吻合度较好,表明以上所建立的分子模型是合适的,采用分子模拟方法能够反映CH4在PVDF中的实际渗透行为。
2.1.2 溶解系数
基于吸附模拟获得CH4在PVDF 中的吸附等温线如图3 所示,其与Langmuir 吸附等温线趋势一致,对应于Langmuir 单层可逆吸附。采用式(2)对图3 中的吸附等温线进行非线性最小二乘法拟合获得不同条件下的溶解系数,并结合不同条件下体系的吸附热Qst绘制于表1 和表2。其中吸附热Qst的大小可以衡量吸附强弱的程度,吸附热越大,吸附越强[23]。

图2 30 ℃、0.1 MPa下CH4分子在PVDF中的吸附等温线和均方位移曲线Fig.2 Adsorption isotherm and mean square displacement curve of CH4 molecules in PVDF at 30 ℃and 0.1 MPa
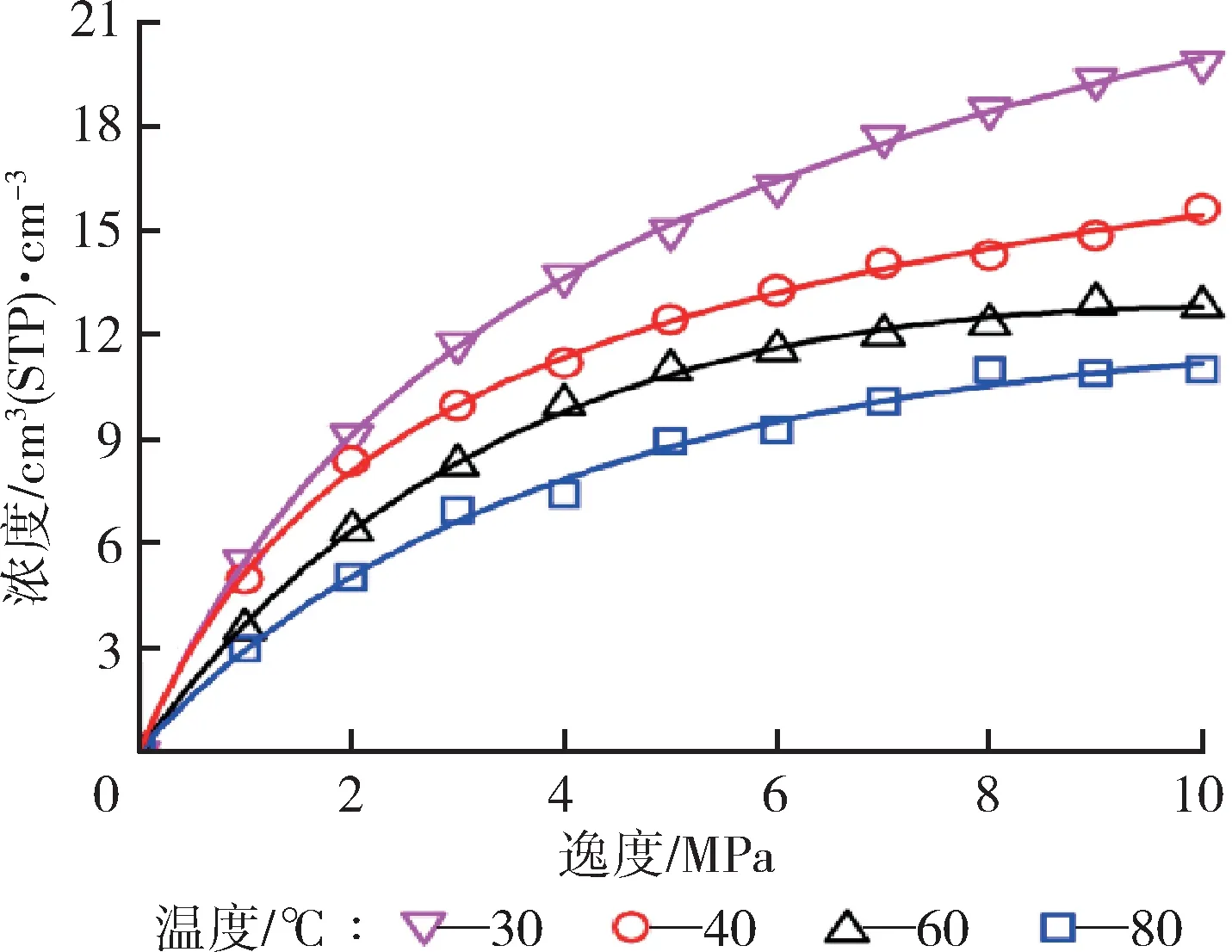
图3 2.5 MPa不同温度时CH4在PVDF中的吸附等温线Fig.3 Adsorption isotherm of CH4 in PVDF under different temperatures at 2.5 MPa
从表1可以看出,当压力一定时,CH4在PVDF中的溶解系数随着温度的升高先增加,在40 ℃时达到最大值后迅速减小。这是由于吸附过程是一个放热过程(Qst>0),当达到吸附平衡时,吸附热会随温度的升高而减小。在低温时,吸附过程在短时间内不能达到吸附平衡;随着温度升高,CH4分子动能迅速增加,热运动加剧,CH4分子和PVDF 链段之间的接触几率增加导致吸附速率增大,吸附热呈现增大的趋势。CH4分子和PVDF链段之间的吸附能力增强使得溶解系数也随之增大。当温度高于40 ℃时,PVDF链段中的吸附位达到饱和平衡状态,吸附热随着温度的升高逐渐减小。这不仅会使PVDF链段的吸附能力下降,还会使PVDF链段对已吸附在其内部的CH4分子的束缚能力下降,CH4分子可克服与其周围聚合物分子的相互作用而逃逸出来,吸附量逐渐减少使得溶解系数也逐渐降低。
温度一定时,不同压力下CH4在PVDF 中的吸附热和溶解系数如表2 所示。可以看出,随着压力增大,CH4在PVDF 中的溶解系数均逐渐增加。这是因为随着压力增大,CH4分子与PVDF 链段之间的吸附热逐渐增大,吸附能力逐渐增强导致各气体分子迅速占据PVDF链段表面的吸附位,溶解系数也显著增加。

表1 2.5 MPa时不同温度下CH4在PVDF中的吸附热与溶解系数Tab.1 Isosteric heat and solubility coefficient of CH4 in PVDF under different temperature at 2.5 MPa

表2 30 ℃时不同压力下CH4在PVDF中的吸附热与溶解系数Tab.2 Isosteric heat and solubility coefficient of CH4 in PVDF under different pressures at 30 ℃
2.1.3 扩散系数
基于Forcite 模块获得CH4在PVDF 中的均方位移曲线如图4 所示。采用式(5)对图4 中各均方位移曲线进行最小二乘法拟合获得不同条件下的扩散系数,如表3和表4所示。
根据Fox 和Flory 的自由体积理论[24],聚合物的体积由高分子占有体积与未被高分子占有的以“空穴”形式存在的自由体积所组成。以“空穴”形式存在的自由体积给聚合物链的运动以及小分子的扩散提供了充足的空间,自由体积大小与扩散系数有着直接的关系。本文使用MS 中的Atom Volume & Surface 模块对PVDF/CH4混合晶胞的自由体积分布图进行模拟研究,结果如图5所示,其中灰色区域为自由体积,其大小以自由体积分数(自由体积与模拟单元总体积的比值)表示。计算得出的不同温度、压力下PVDF/CH4混合晶胞的自由体积分数列于表3和表4。
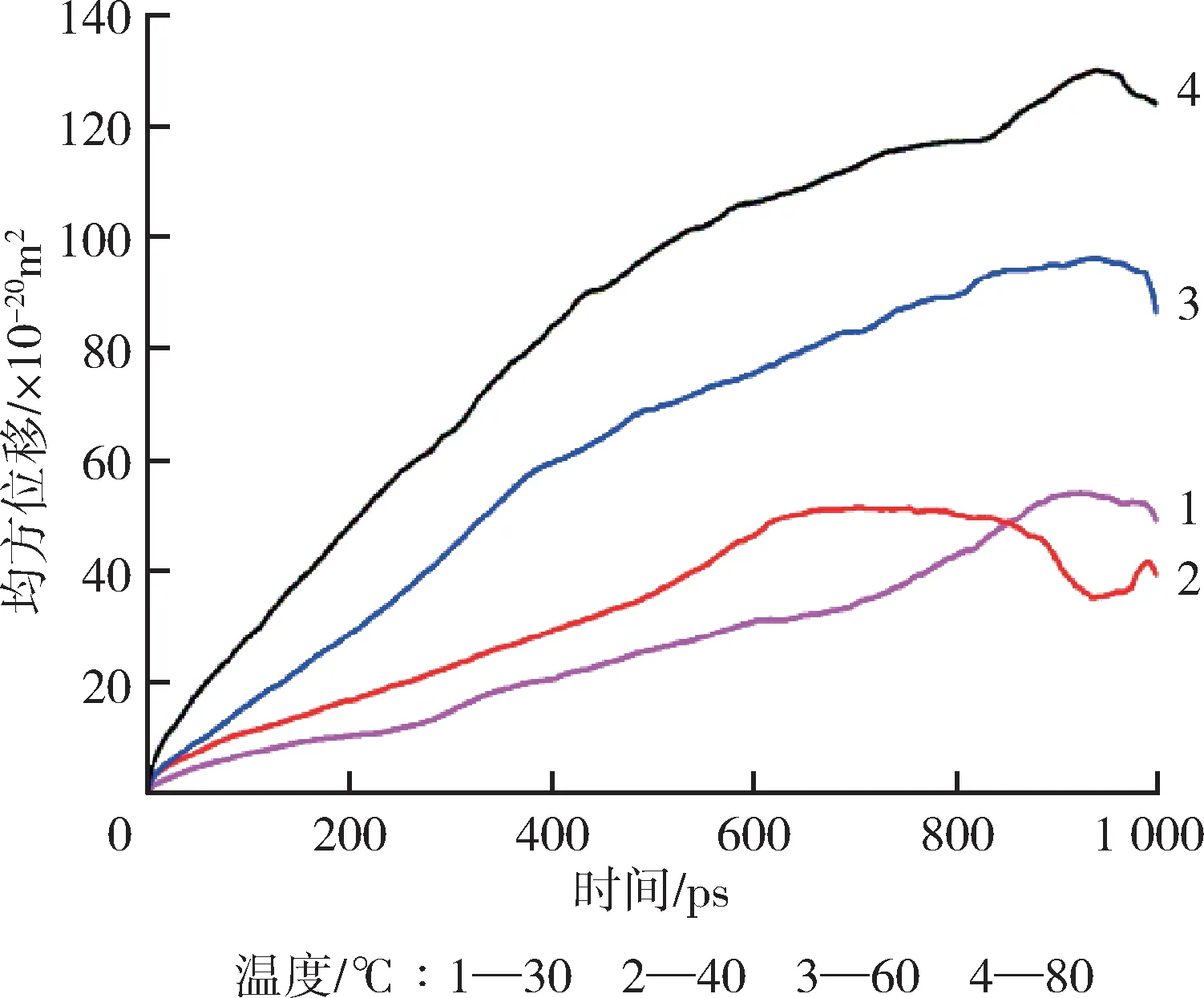
图4 2.5 MPa时不同温度下CH4在PVDF中的均方位移曲线Fig.4 Mean square displacement curve of CH4 in PVDF under different temperatures at 2.5 MPa
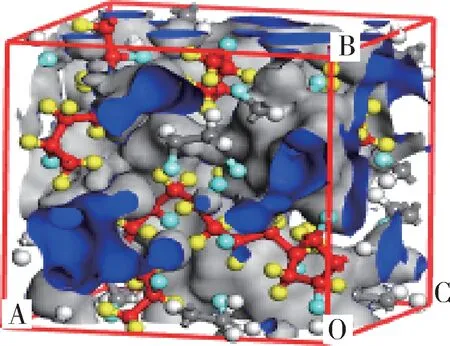
图5 PVDF/CH4混合晶胞的自由体积分布图Fig.5 Free volume distribution of PVDF/CH4 mixed cells
由表3可知,当压力一定时,CH4分子在PVDF中的自由体积分数和扩散系数均随着温度升高而增大。这是由于温度升高会导致PVDF 链段的热运动加剧从而产生更大的构象数,形成更多的自由体积,使得CH4分子在聚合物中自由运动的空间大大增加,扩散过程更加容易进行,扩散系数逐渐增加。另外,温度升高也会增加分子链的活动性,链段更容易发生扭转或进行相对运动,使小分子扩散通道出现的几率增加,从而缩短CH4分子发生跃迁的时间间隔,使跃迁的频率更高。其次,温度升高导致CH4分子的热运动更加剧烈,更容易摆脱空穴的束缚,这也进一步导致扩散系数随温度升高而增大。
温度一定时,不同压力下CH4在PVDF 中的自由体积分数和扩散系数如表4所示。可以看出,自由体积分数和扩散系数均随着压力的增大而增大。这是由于压力升高会使PVDF 分子链的刚性降低而柔顺性增加,链段更易发生剧烈运动形成更多的自由体积,增大了CH4分子从一个自由体积空穴跃迁到另一自由体积空穴的可能性,扩散系数随之增加。此外,压力升高使得PVDF 链段的活动加快,有利于空穴之间通道的形成,从而使CH4分子在PVDF 中的空穴跳跃更加频繁,扩散系数也逐渐增加。

表3 2.5 MPa时不同温度下CH4在PVDF中的自由体积分数和扩散系数Tab.3 Fractional free volume and diffusion coefficient of CH4 in PVDF under different temperature at 2.5 MPa
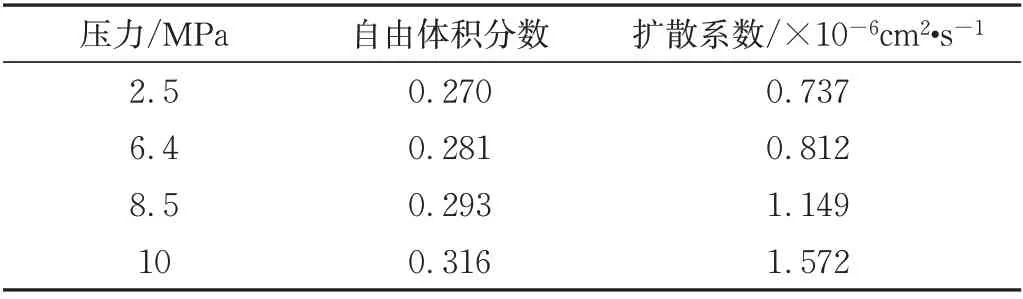
表4 30 ℃时不同压力下CH4在PVDF中的自由体积分数和扩散系数Tab.4 Fractional free volume and diffusion coefficient of CH4 in PVDF under different pressure at 30 ℃
综上,温度和压力升高均会导致模拟晶胞的自由体积分数增大从而加快扩散过程的进行,使扩散系数呈现逐渐增大的趋势。对比自由体积分数和扩散系数的增长幅度还可以看出,温度对自由体积分数和扩散系数的影响要高于压力的影响。
2.1.4 渗透系数
基于以上溶解系数和扩散系数,结合(1)式计算获得不同条件下CH4在PVDF 中的渗透系数,如表5 和表6 所示。随着温度升高,渗透系数先增加后略有减小;随着压力增加,渗透系数稳步增长。渗透系数的变化趋势与溶解系数的趋势(表1 和表2)一致,说明CH4在PVDF 中渗透时,渗透系数的大小主要取决于气体分子在聚合物中的溶解系数。
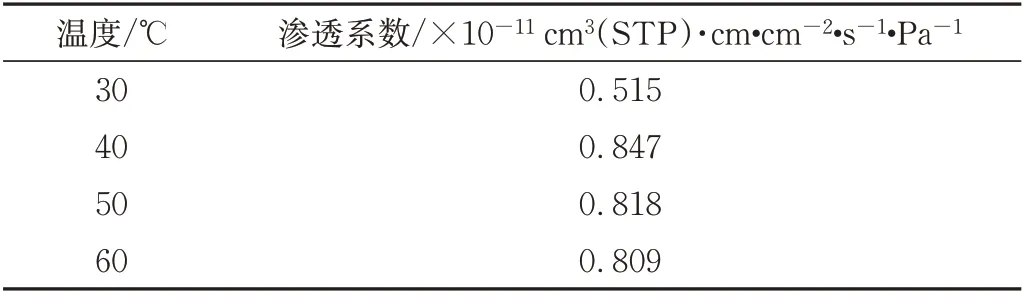
表5 2.5 MPa时不同温度下CH4在PVDF中的渗透系数Tab.5 Permeability coefficient of CH4 in PVDF under different temperature at 2.5 MPa

表6 30 ℃时不同压力下CH4在PVDF中的渗透系数Tab.6 Permeability coefficient of CH4 in PVDF under different pressure at 30 ℃
2.2 CH4分子在PVDF中的渗透机理
渗透机理包括吸附机理和扩散机理:通过CH4分子在PVDF 表面的吸附密度场分布图和等密度显示图对吸附机理进行分析;通过CH4分子在PVDF 中的扩散轨迹以及扩散位移进行扩散机理研究。
2.2.1 密度场分布图和等密度显示图
图6为30 ℃、2.5 MPa下CH4在PVDF中的吸附密度场分布图和等密度显示图,其中等密度面上的颜色描述了对应的能量场值。图6(a)中的散点区域代表气体分子在PVDF模拟单元中的密度集中分布区域,即溶解的分子集中分布的位置,表明CH4在PVDF中的吸附呈聚集分布。根据图中右侧密度与颜色对应表可以看出,在空穴中心吸附密度最大,次外层次之,最外层密度最小。从图6(b)的等密度显示图的情况可以看出,蓝色区域(数值大)代表该区域的分子间作用能高,处于模拟单元中吸附的高能量区域,蓝色越深表示能量越高。红色区域(数值小)代表该区域的分子间作用能低,处于模拟单元中吸附的低能量区域,红色越深表示能量越低。在模拟过程中,红色区域是气体分子吸附的“热点”,也就是最容易吸附的位置,这与密度场分布图反应的情况一致。综合密度场和能量场分布图可以看出,CH4在PVDF中的吸附不是均匀吸附,而是有选择性的聚集吸附,且吸附位置位于模拟单元中的低势能区。

图6 CH4分子在PVDF中的吸附密度场分布和等密度Fig.6 Density field distribution and isopycnic of CH4 molecules in PVDF
2.2.2 扩散轨迹和位移
图7~8 分别是不同温度和压力下单一CH4分子在PVDF内的三维运动轨迹图和扩散位移时间图。从图7可以看出,在2.5 MPa 下,当温度为30 ℃时,CH4分子大部分时间是在小范围内进行空穴内运动[图7(a)],运动位移始终保持在0.05 nm 以内[图7(b)]。当压力不变而温度升高至40 ℃时CH4分子在空间内的扩散轨迹变得更加散落[图7(a)],当扩散继续进行时,CH4分子在0~600 ps 内先后出现了5 次较大范围的空穴间跃迁,跃迁距离为0.2 nm 左右,扩散能力变强[图7(b)]。从图8 可以看出,温度相同下,当压力从2.5 MPa 升高至6.4 MPa时,扩散轨迹不再集中分布[图8(a)],空穴间的跃迁次数明显增多,跃迁距离明显增大[图8(b)]。由上可以看出,温度和压力的升高均会使CH4分子在PVDF中的扩散能力变强。
综合图7 和图8 还可以看出,CH4分子在PVDF 内大部分时间是在很小的范围内运动,可以看作是空穴内振动。当温度和压力增大时,一方面使得CH4分子自身热运动加剧,更容易摆脱空穴的束缚,进而进行大范围的空穴间跃迁;另一方面还会导致PVDF 链段的热运动加剧,不仅会形成更多自由体积还会加快扩散通道的出现,从而使CH4分子从一个自由体积空穴跃迁到另一自由体积空穴的频率增大,CH4分子在PVDF中的扩散也从空穴内运动转变为空穴间运动。以上模拟结果验证了小分子在聚合物中以空穴形式存在的自由体积之间的扩散模式,与陶长贵等[12]分析的小分子在聚合物内的扩散机理基本一致。

图7 2.5 MPa时不同温度下单一CH4分子在PVDF内的三维运动轨迹和扩散位移时间Fig.7 Diffusion trajectory and displacement of a CH4 molecule in PVDF under different temperatures at 2.5 MPa
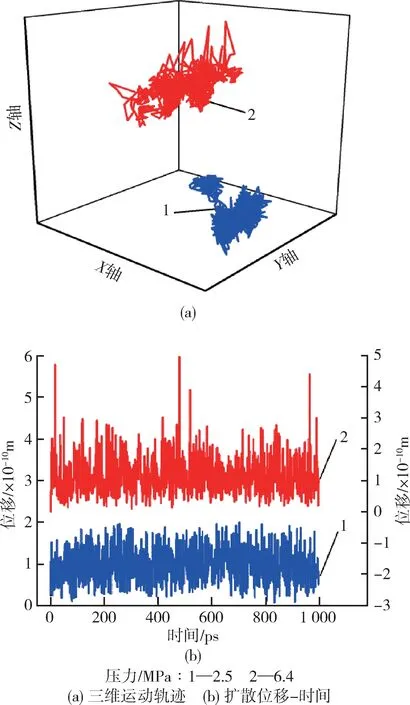
图8 30 ℃时不同压力下单一CH4分子在PVDF内的三维运动轨迹和扩散位移-时间Fig.8 Diffusion trajectory and displacement of a CH4 molecule in PVDF under different pressure at 30 ℃
综上分析可知CH4在PVDF的渗透机理为:CH4分子首先在PVDF内呈现有选择性的聚集吸附,且多吸附于晶胞中的低势能区;随后,吸附在PVDF 内的CH4分子在以空穴形式存在的自由体积之间进行扩散。温度越高、压力越大,CH4分子在PVDF中扩散能力也越强。
3 结论
(1)CH4在PVDF 中的溶解系数、渗透系数随温度的升高先增大后减小,随压力的升高而升高;扩散系数和自由体积分数均随温度和压力的升高而增大;
(2)CH4在PVDF 内呈现有选择性的聚集吸附,且多吸附于模拟晶胞中的低势能区;低温低压下CH4分子在PVDF 内的扩散以小范围的空穴内振动为主,当温度或压力增大时会出现较大范围的空穴间跃迁。
