新型混合改进遗传算法求解零等待流水车间调度问题

裴小兵，李依臻

(天津理工大学管理学院，天津 300384)

0 引言

在制造系统领域，车间调度是一个重要的研究课题，合理的调度计划可以有效地减少浪费，为企业创造更好的经济效益。车间调度问题分为单机调度问题、流水车间调度问题和作业车间调度问题[1]。在工业生产领域，流水车间调度问题(Flow shop Scheduling Problem，FSP)是一个通用的问题模型，同时也是学术领域研究的热点。流水车间调度问题包含置换FSP、零等待FSP、阻塞FSP、零空闲FSP和混合FSP。本文研究了零等待流水车间调度问题(No-wait Flow Shop Scheduling Problem，NWFSP)，且已经证明机器数大于2时，NWFSP是一类NP-hard问题[2]。零等待约束广泛存在于钢铁冶炼、食品加工、生物制药和化工等生产过程中，即加工过程一旦开始将不能中断，直到完成所有加工工序。例如，钢铁生产中为防止金属温度降低而导致成份破坏，其轧制过程必须连续无间断地完成;塑料成型过程中所有工序之间必须不间断地连续完成，以防止塑料成份降解退化。

随着问题规模的扩大，通过分支界定法或混合整数规划法等精确算法求解NWFSP，难以在合理的时间内得到结果，因此，需要进一步研究其他有效算法求解该问题。近几年，已经提出各种有效的优化算法用于求解复杂优化问题，如回溯搜索算法[3]、教与学算法[4]、猴群算法[5]、鲸鱼优化算法[6]等。Laha等[7]提出了基于惩罚的匈牙利算法求解NWFSP，采用基于惩罚的策略产生初始调度，并运用3种插入方法提高初始解的质量，实验结果表明所提算法的计算结果均优于现存优化算法。Ye等[8]以完工时间最小化为目标，提出了平均撤出时间启发式求解NWFSP，插入过程采用目标值增量法来降低算法的计算复杂度，实验结果验证了相同计算复杂度情况下，所提启发式方法比其他启发式方法更优。仲维亚等[9]研究了两阶段零等待流水作业排序问题，提出了两个近似算法，并通过数值分析验证了算法的性能。Ding等[10]结合禁忌搜索机制提出了改进迭代贪婪算法求解NWFSP，该算法采用基于禁忌表重组策略和变邻域搜索策略提高解的质量，运算结果表明了所提算法比其他启发式算法具有更好的性能。针对NWFSP 的特点，Zhao等[11]提出了具有种群适应机制的基于因子的粒子群优化算法，算法采用变邻域局部搜索机制提高种群的质量，通过种群适应机制控制种群多样性，避免算法陷入局部最优，最后通过标准算例对算法进行了测试，算例求解结果表明了文中所提算法的优越性。宋存利等[12]针对大规模NWFSP的特点提出了邻域迭代搜索算法，并以最小化完工时间为目标，通过仿真实验验证了所提算法性能的高效性和有效性。Riahi等[13]结合模拟退火算法提出新型混合蚁群算法求解NWFSP，该算法在增加种群多样性和改善传统蚁群算法容易陷入局部最优问题上有了明显的提高。李永林等[14]提出一种混合群搜索算法，并根据NWFSP的特点设计了一种完工时间的简化计算方法和有效的局部搜索策略，有效地平衡了计算代价与性能。Engin等[15]结合遗传算法的交叉和变异机制来避免蚁群算法陷入局部最优解的可能，采用全局更新规则实现种群进化，计算结果验证了所提算法相对于其他算法具有更好的性能。

上述文献中的算法在解决NWFSP时均求得了较优的结果，为算法的初始化、局部搜索策略、全局改善机制以及种群多样性等方面提供了积极的借鉴意义和理论基础。遗传算法(Genetic Algorithm，GA)[16]是目前发展比较成熟的一种优化算法，具有较高的通用性、潜在的并行性和较佳的全局搜索能力等特点，被广泛应用于求解车间调度问题中。Yu等[17]运用遗传算法解决混合流水车间调度问题，采用一种新的解码机制，从给定的工件排序中改进调度构建过程，然而遗传操作过程采用随机方式无法避免交叉和变异过程中的无效操作。Deng等[18]提出协同进化量子遗传算法求解零等待流水车间调度问题，以方阵表示量子个体，更容易得到工件排序，但并未降低问题复杂度，对于大规模问题运算时间会大大增加。崔琪等[19]提出改进混合变邻域搜索的遗传算法求解混合流水车间调度，但是仅使用反转逆序变异的方式无法有效地避免算法陷入局部最优解。通过查阅和分析文献可知，国内缺乏运用GA求解NWFSP的研究，且运用遗传算法求解调度问题仍存在较大的改进空间。

区块、关键块或优势块是近年来提出的一种新理论，在降低问题复杂性、提高算法求解速度、改善解的质量方面优势明显。Chang 等[20]依据二元变量概率模型，结合概率矩阵和轮盘赌法挖掘优势块，运用二元变量概率模型提出了基于块的分布估计算法求解FSP。Hsu等[21]则运用关联规则挖掘优势个体的基因组合组成优势块，大大提高了运算效率。

随着对GA研究的逐步深入，许多学者将该算法应用求解调度问题中。本研究针对NWFSP问题提出了新型混合改进遗传算法(New Hybrid Improving Genetic Algorithm，NHIGA)。首先，通过改进NEH(Nawaz-Enscore-Ham)算法获得具有较优质量和多样性的初始种群。为加快算法求解效率、降低问题复杂性，采用关联规则挖掘优势染色体上的优势块，加快算法迭代效率。此外，通过改进交叉和变异过程进一步改善遗传算法的全局和局部搜索能力。本研究还提出了基于NEH(Nawaz-Enscore-Ham)算法的邻域搜索机制，通过扩大搜索范围，进一步提高算法的质量。最后，通过仿真实验验证了本文算法求解NWFSP的有效性和鲁棒性。

1 问题描述

NWFSP可以定义如下:在m台机器M={M1，M2，…，Mm}上按顺序加工n个工件J={J1，J2，…，Jn}，工件的加工路径均相同。Pj，i表示工件Jj在机器Mi上的加工时间，j∈{1，2，…，n}，i∈{1，2，…，m}，工件的加工时间已知。问题的约束条件如下:机器在同一时间只能加工一个零件，且该时间一个工件只能在一台机器上加工;工件从开始加工到完成，加工过程中无任何等待时间。调度的目的是找到工件最佳的加工顺序，本研究以最小化完工时间Cmax为目标，则目标函数如式(1)所示。

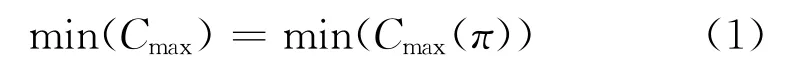
假设一个可行调度序列π={π1，π2，…，πj，…，πn}，由于零等待条件的约束，相邻两工件πj和πj+1在第一台机器上加工时存在开工时间差Ej，j+1，Ej，j+1的计算公式如下[22]:

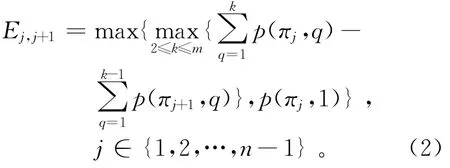
因此，可行调度π的完工时间Cmax的计算公式如下:

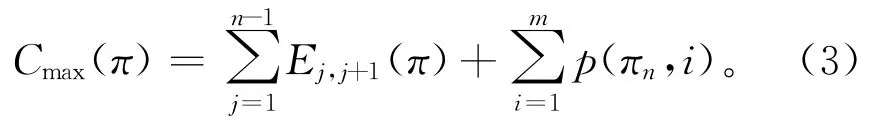
同时，NWFSP问题还需满足下列条件[23]:

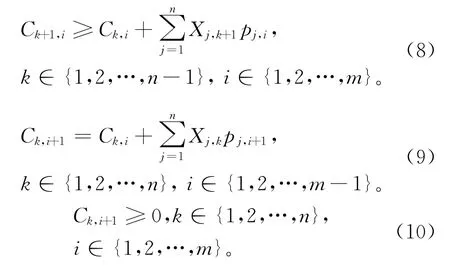
式(4)表示决策变量;式(5)和式(6)确保了在一个调度序列中，所有工件仅出现一次;式(7)表示第一个工件在第一台机器上的完工时间，确保了第一台机器的开工时间为零;式(8)为每一台机器上相邻两工件之间的关系，确保一台机器在同一时刻不能同时加工多个零件;式(9)表示同一工件相邻工序之间完工时间的关系，确保问题满足零等待约束条件;式(10)保证了所有工序的完工时间均大于零。

2 新型混合改进遗传算法求解NWFSP

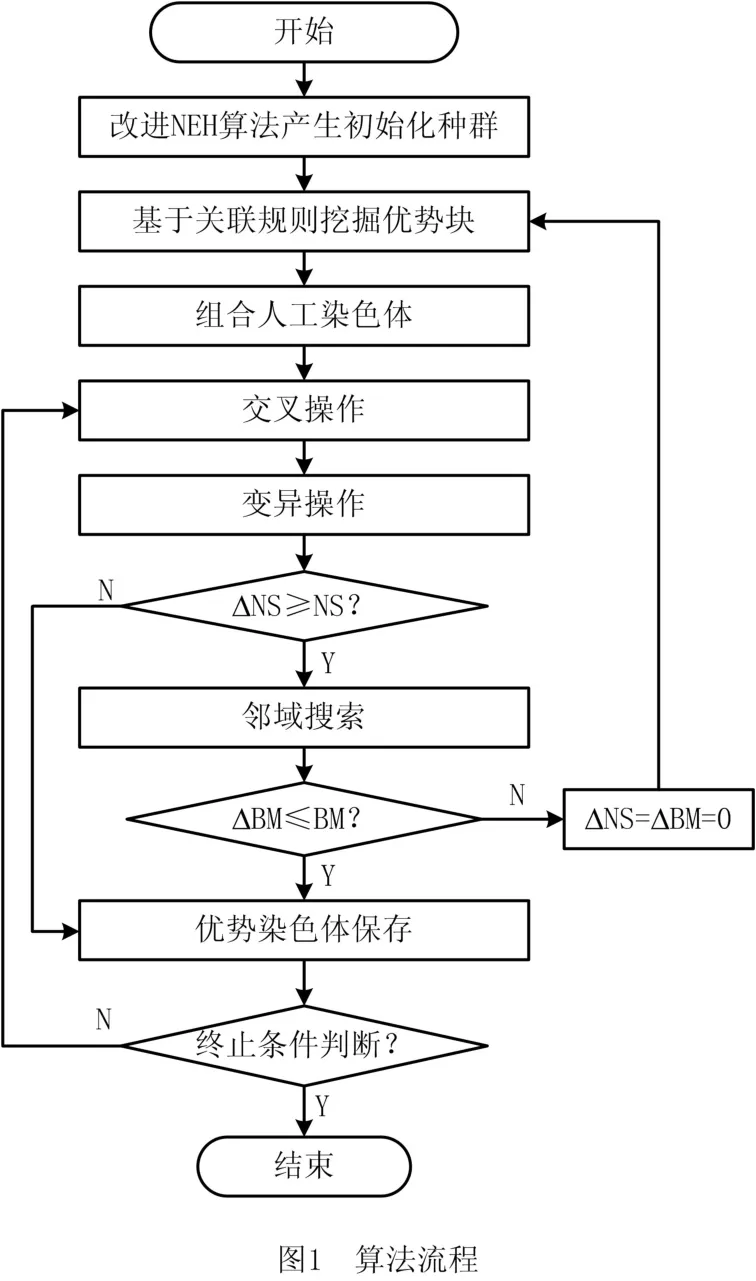
考虑到GA 算法的优点，本研究结合NWFSP自身特点，提出了新型混合改进遗传算法(NHIGA)，其流程图如图1所示。图中:ΔNS表示邻域搜索计数器;NS表示邻域搜索范围临界值;ΔBM表示优势块挖掘计数器;BM 表示优势块挖掘临界值。NHIGA主要分为6个部分:①初始化种群;②基于关联规则的优势块挖掘;③人工染色体组合;④遗传操作;⑤邻域搜索机制;⑥优势染色体保留机制。各部分的具体操作如下文所述。

2.1 初始化种群

本研究以加工工件的编号作为染色体的基因，一个完整的染色体由所有工件的排序组成，工件的个数n即为染色体长度。通过种群初始化构造具有较高质量的初始染色体种群，达到改善算法求解效率的目的。

NEH 算法[24]是最常用的初始化方法，本研究根据NEH 算法的思想，结合NWFSP的特点，提出了改进NEH 启发式算法产生初始化种群。首先，根据NEH 算法生成一条染色体;然后，在该条染色体的基础上实施破坏性重组;从所得邻域中选择最优染色体替换初始染色体。重复上述过程，直到获得NP(种群数量)个初始个体。具体操作如下:

步骤1计算每一个工件从机器1到机器m的加工总时间Tj，并将Tj按降序进行排列，构成工件序列T。Tj计算公式如下:

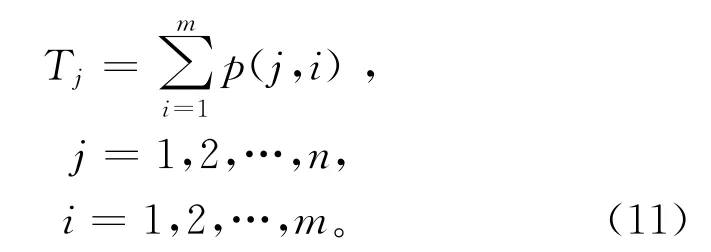
步骤2选择T中的前两个工件，并计算两个工件组成的两个排序的总完工时间，保留完工时间最小的排序。

步骤3按照降序选取T中的一个工件，并依次插入到当前序列的所有可能位置，每插入一个位置计算该位置形成的序列的完工时间，最终将总完工时间最小的序列作为下一个工件插入的基础。

步骤4重复步骤3，直到所有工件都完成插入，形成完整序列π。

步骤5随机选择π中k个工件实施破坏重组操作，并对k个工件按Tj的降序进行排列形成T'。将π中未被选中的工件组成新的排列π'。

步骤6选择T'中第一个工件，将其插入π'中所有可能的位置，并计算对应的完工时间Cmax，保留Cmax值最小的序列作为T'中下一个工件插入的基础序列，重复该步骤直到T'中的工件全部插入到π'中，得到第二条初始染色体。

步骤7重复步骤5和步骤6，直到形成完整的初始种群NP。

2.2 基于关联规则的优势块挖掘

优势染色体之间的基因结构是具有一定规律的，通过寻找这种规律，将其组合成优势块可以大幅降低问题复杂度、提高算法求解效率、改善求解质量。本研究基于关联规则挖掘优势染色体上的优势基因块组成优势块，以提高算法的求解效率，改善算法的整体性能。

2.2.1 关联规则

关联规则[25]是数据挖掘中一种常用的方法，可有效改善数据结构，提高算法求解性能。本研究通过关联规则分析染色体的结构，发现基因之间的相关性，寻找优势基因组成优势块，通过将优势块直接注入人工染色体来降低问题的复杂度。

A与B之间关联规则的表达存在支持度和信心水平[26]两个重要的参考指标。支持度表示A与B同时出现在数据记录中的频率;信心水平表示A与B之间的关联强度。关联强度的评判指标增益值表示关联度的强弱，若增益值大于1，则表示强关联。对应计算公式如下:

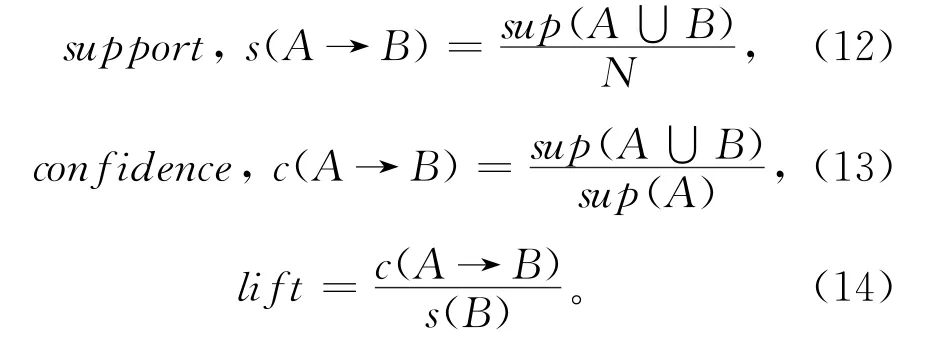
上述公式中，A→B表示若A发生，则B也发生;N为染色体总数;sup(A∪B)表示各染色体上同时出现基因集A和基因集B的总次数;sup(A)表示基因集A出现在各个个体中的总次数;s(A→B)为A和B之间关联支持度的强弱;c(A→B)为A和B之间关联信心水平;lift表示评价指标增益值，其作用是判定A与B之间是否具有强关联性。此外，为保证关联法则的有效性，需设置最小支持度和最小信心水平，当所挖掘个体之间的关联评价指标满足设立的最小临界值时，则视为有效关联，并进行保留。

2.2.2 挖掘优势块

优势块是染色体上优势基因之间的结构组合，在降低算法复杂度上具有明显的效果。本研究采用关联规则挖掘优势染色体中的优势块，寻找优势基因结构组合成优势块。首先，将各代群体中的染色体依据适应度值从小到大的顺序进行排序，选择前k条染色体，将所选染色体上的工件加工顺序转换为工件加工记录资料。以工件5和机器5为例，如图2所示为染色体转化过程。

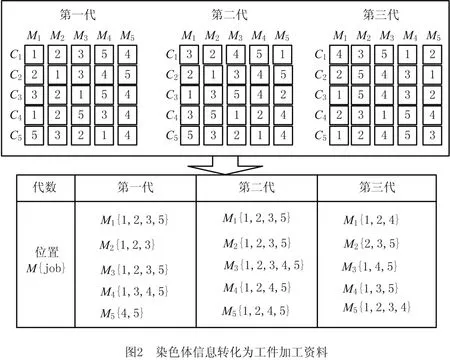
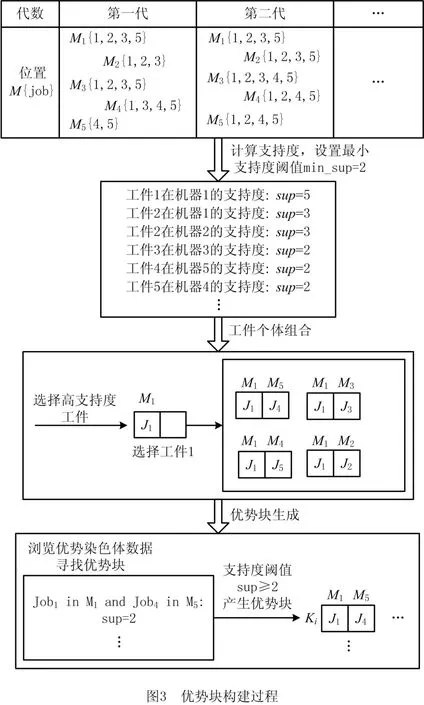
设立最小支持度水平(support)临界值和优势块长度，找出所得到的工件加工数据集中大于临界值的工件及对应机器。具体操作步骤如下:

步骤1选择工件加工数据集中大于临界值的基因放入频繁项目集F中。

步骤2将频繁项目集F中的基因组合成优势块放入候选项目集C中。

步骤3观察候选项目集C，将所有大于临界值的优势基因进行组合，形成新的频繁项目集H'。

步骤4重复上述步骤，直到将所有优势基因组合存入暂存资料库。

如图3所示为优势基因块的构建过程。

2.2.3 优势块筛选

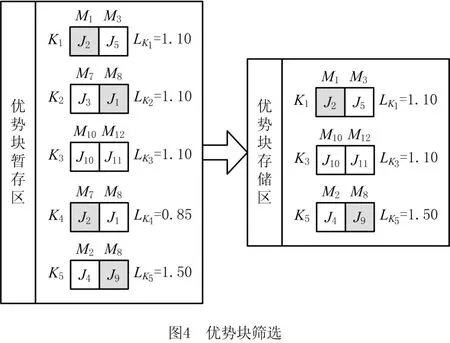
由于依据关联规则挖掘产生的优势块之间存在工件或机器的重叠，需要通过比较优势块暂存器中的优势块进行筛选，通过优势块之间的竞争，最终形成具有高度竞争优势的优势块。具体操作如下:首先，对比暂存器中优势块的工件与机器，若各优势块之间出现重复的工件或机器，则计算优势块的增益值[27]，增益值大于1且数值较大的优势块具有更强的关联度，对其进行保留，不满足要求的则删除。优势块的筛选过程如图4所示，经过竞争留存下来的优势块将用于组合人工染色体。

2.3 人工染色体组合

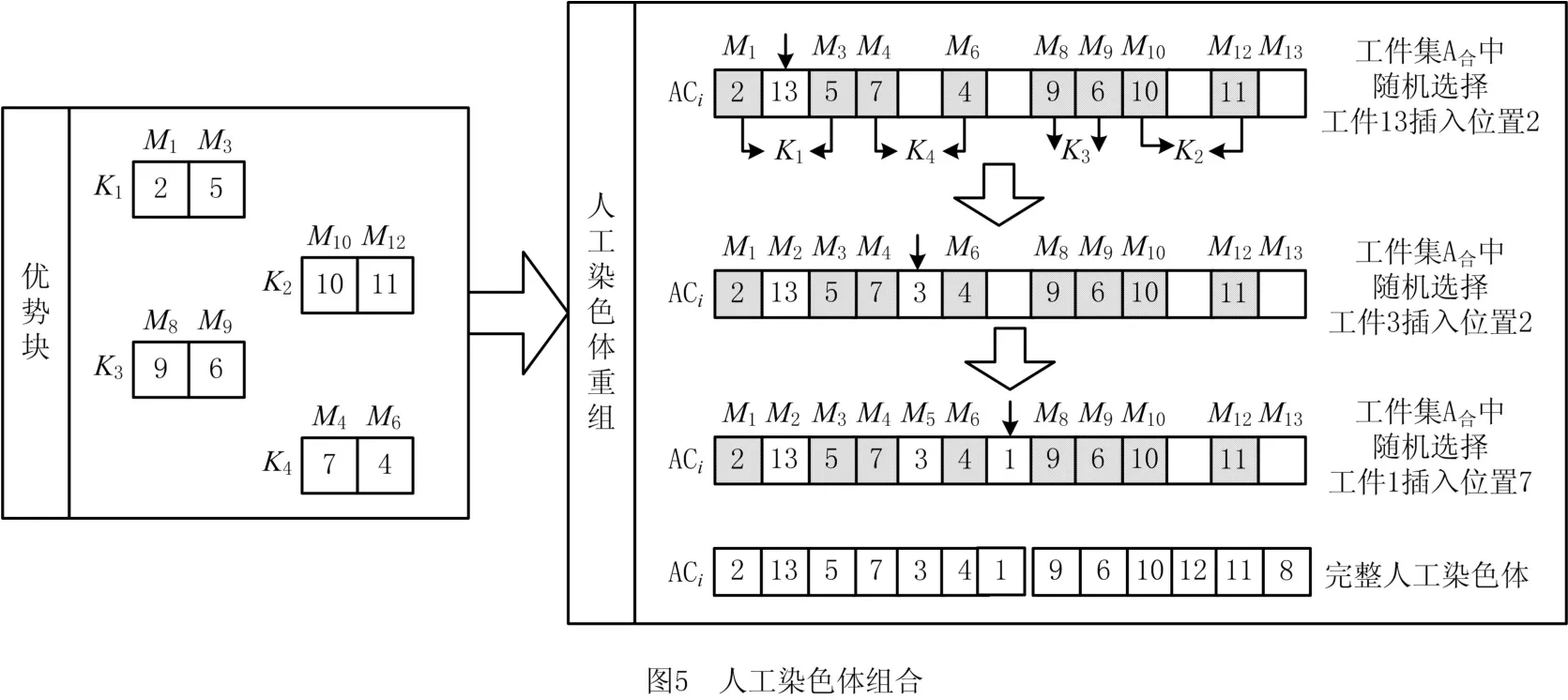
人工染色体组合可以获得具有高度竞争优势的染色体种群。本研究利用关联规则挖掘和筛选出来的优势块组合人工染色体，具体操作步骤如下:将优势基因块直接复制到人工染色体上的对应位置;然后，将尚未分配的非优势块上的基因以随机的方式插入人工染色体的空白位置，直到所有基因均插入到人工染色体中，形成完整的人工染色体。如图5所示为人工染色体组合方式。

2.4 遗传操作

2.4.1 交叉算子

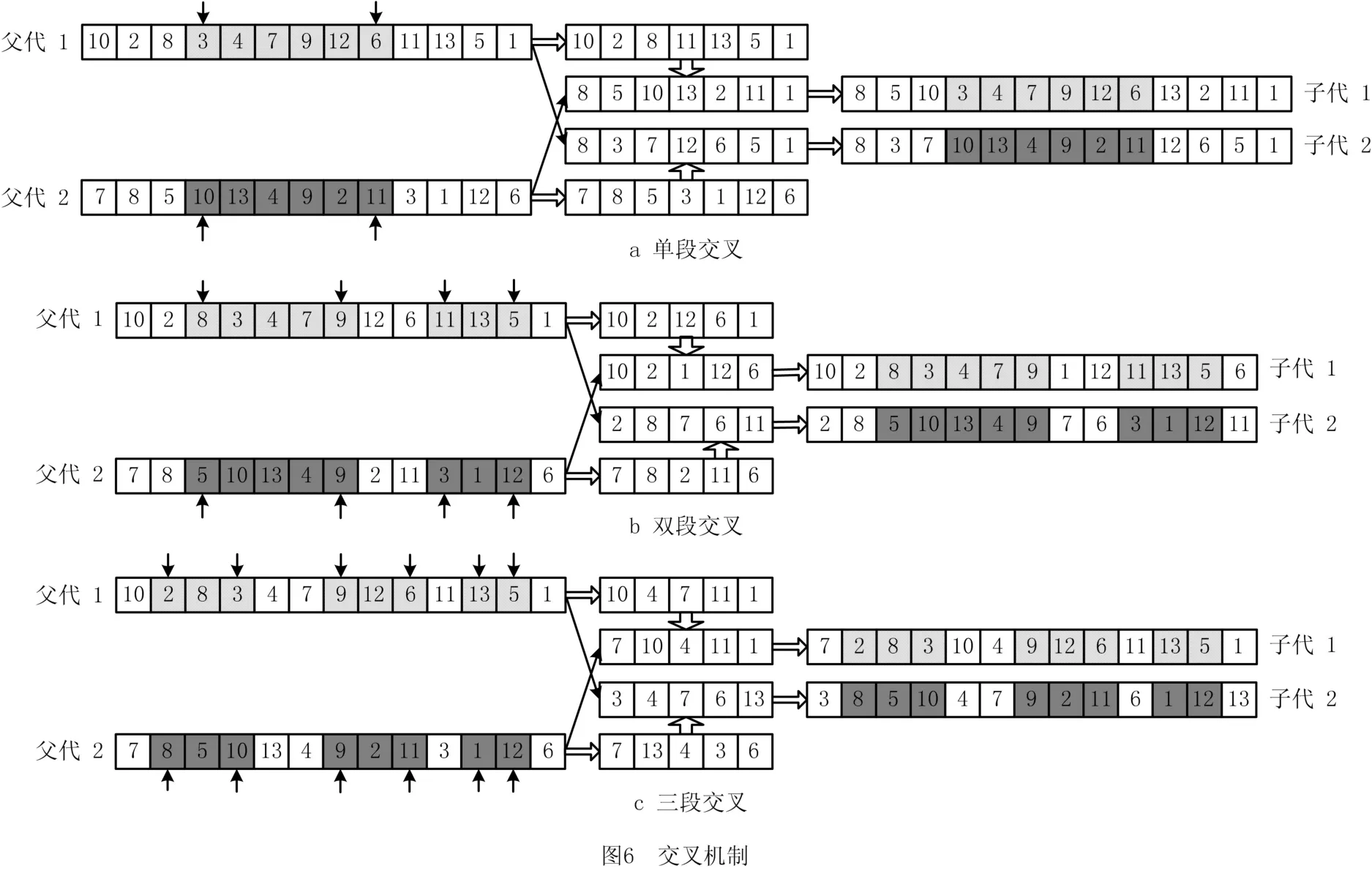
在GA中，通过两个原有染色体之间的交叉，可能会得到更优异的染色体，从而实现种群的进化。求解FSP的GA 大多数交叉算子均采用基于位置的交叉或两点交叉机制。本文根据NWFSP的特点，设计了3种不同的交叉机制，分别为单段交叉、双段交叉和三段交叉，以提高算法求解质量，实现种群进化。首先，随机选择交叉个体父代1和父代2，并选取两个父代上相同位置的基因段，被选择的基因段直接复制到子代;然后，父代1上的剩余基因依据父代2上基因出现的顺序重新组合，父代2上的剩余基因依据父代1上基因出现的顺序重新组合;最后，将重组后的基因段依序插入到对应的子代中。图6展示了3种交叉方式的交叉过程。

2.4.2 变异算子

交叉操作改善了算法的全局搜索能力，提高了种群的整体质量，但较优个体过度集中容易导致算法陷入局部最优，因此在交叉操作的基础上执行变异操作，通过增强染色体基因突变能力，提高算法的局部搜索性能。变异操作用于全局寻优过程，当个体趋于最优解时，有利的变异可以提高种群的质量。为了使变异过程具有方向性和目的性，本研究结合种群分割的概念[28]，提出了基于种群分割思想的变异操作机制，通过执行有效的种群分割，得到染色体质量不同的两个子种群，分割后的两个染色体子种群分别赋予不同的变异概率，以保证染色体变异的有效性。

(1)水平集定义 设第G代变异染色体种群包含个体集合为POP={AC1，AC2，…，ACn}，染色体规模为n，适应度函数为Cmax(i)，称集合:

(2)种群分割定义 将所得染色体中种群集合POP，按照适应度值的升序进行排列，根据水平集的概念，将大于或等于的最小位置作为种群分割点，把种群分割成两部分，大于等于的部分记为Uac，小于的部分记为Lac。

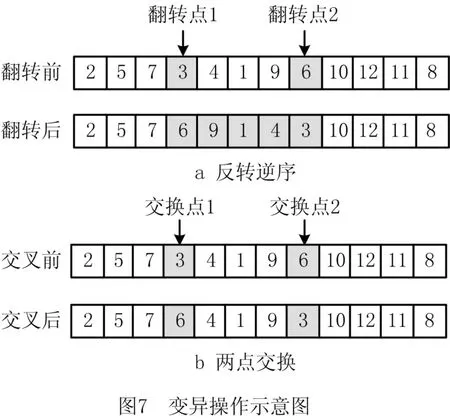
种群分割可以有效避免变异的无效性，提高算法局部寻优能力。较优的染色体子种群进行小概率变异，变异概率为Pm1;次优的染色体子种群进行较大概率的变异，变异概率为Pm2。本研究采用两种变异机制，首先随机产生两个变异点，然后分别采用两点交换和反转逆序的两种变异机制扩大搜索空间，以便能产生更好的扰动，避免算法陷入局部最优解。图7为变异操作示意图。

2.5 邻域搜索机制

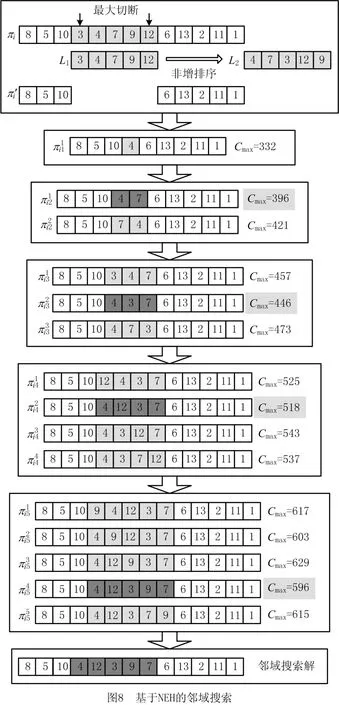
邻域搜索的关键问题是如何设计最优解的邻域。本研究根据NWFSP问题的特点，运用NEH算法的思想，提出了基于NEH 算法的邻域搜索机制。具体操作步骤如下:

步骤1随机选择染色体上L个基因位点，识别出两个连续基因位点之间最长的片段记为L1，剩余染色体上其他基因位置不变，并记为。

步骤2计算L1上各工件在机器加工过程的总时间，并按工件加工完成时间的非增顺序进行排列，得到L2。

步骤3依据NEH 算法规则，将L2上的工件依序插入到染色体的切段位置，并计算适应度值，将适应度值最优的个体作为下一工件插入的基准。

步骤4当L2上所有工件插入完成后，将适应度值最优个体作为邻域搜索的结果，即为邻域搜索解。

如图8所示为邻域搜索的过程示意图。

2.6 优势染色体保留机制

将邻域搜索所产生的子代染色体与此代的原始染色体进行比较筛选，本文采用二元竞赛法[29]选择新的种群进入下一代的进化过程。二元竞赛法的操作过程如下:首先，将新的子代染色体与原始染色体放入同一个选择池中;然后，从选择池中随机选择两条染色体，比较各自对应的适应度值，适应度值小的染色体将被选作新的种群，适应度值大的将被放回选择池继续进行筛选;反复执行上述步骤，直到所选染色体满足种群大小，新的种群将进入算法的下一次迭代过程。

3 仿真实验

3.1 实验设置

选择Carlier[30]、Reeves[16]和Taillard[31]的基准算例进行实验验证。算法程序在MATLAB 2016b进行编写，运行环境为Windows10(64位)操作系统，处理器为Intel(R)Core(TM)i5-4200M CPU@2.50GHz 2.50GHz，内存为8 G 的环境下运行。为了证明本文所提算法的有效性，并能直观地看出与其他算法比较所得结果的优越性，所有算法运行结果均通过平均相对百分比偏差(ARPD)进行评估。ARPD的计算公式如下:

式中Ck表示对给定问题进行第k次实验时算法所得到的解，Copt表示当前所求问题的最优解。显然，ARPD的值越小，则算法的性能越好。此外，实验过程还记录了算法运行结果的标准偏差(SD)，以此来分析算法的鲁棒性。SD的计算公式如下:

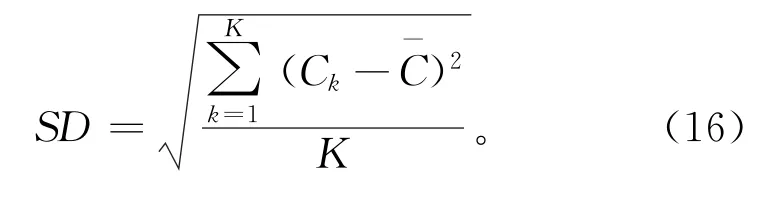
本文所提算法运行过程中的相关参数设置如表1所示，每个算例运行10次，选取最优结果作为输出解，设置算法的运行时间为(n2/2×10)ms。

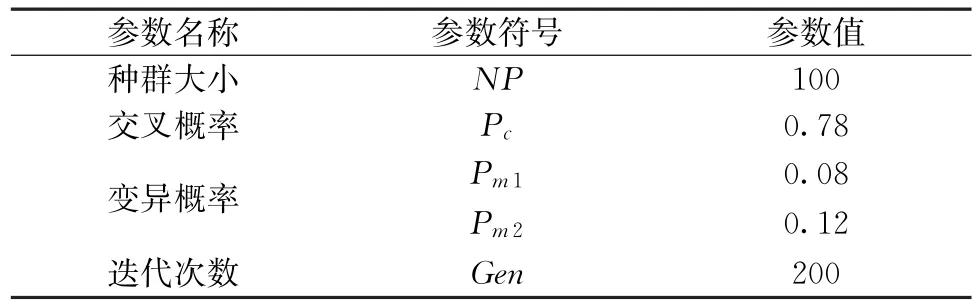
表1 参数表

3.2 算法比较

为证明本文所提NHIGA 的求解性能，将本文算法与文献[10]中的禁忌搜索机制改进迭代贪婪(Tabu-Mechanism Improved Iterated Greedy，TMIIG)算法、文献[32]中的基于概率性的教与学机制的元启发式(meta-heuristic based on Probabilistic Teaching-Learning Mechanism，mPTLM)算法和文献[33]中的离散水波优化(Discrete Water Wave Optimization，DWWO)算法进行了对比。为阐明本文所提算法的有效性，分别从计算结果的精度、离散程度和收敛性进行了分析比较。实验过程设置了相同的运行环境和运行时间，以保证比较结果的精确性和可靠性。

表2显示了Carlier算例的运行结果。如表2所示，NHIGA 求得的ARPD的平均值为0，相对TWMIIG 和mPTLM 算法所求得的0.003 与0.001，NHIGA的计算精度更高。同时，DWWO算法求得的ARPD平均值与NHIGA所求值相等，在小规模问题上两者的求解精确性均较优。标准偏差SD值反映了算法运行的稳定性，其值越小，算法的稳定性更好。由表2可知，NHIGA求得的SD平均值为0，均低于其他3种算法所求结果。综上分析，本文所提算法在求解小规模问题上具有较好的求解精度和较高的稳定性。

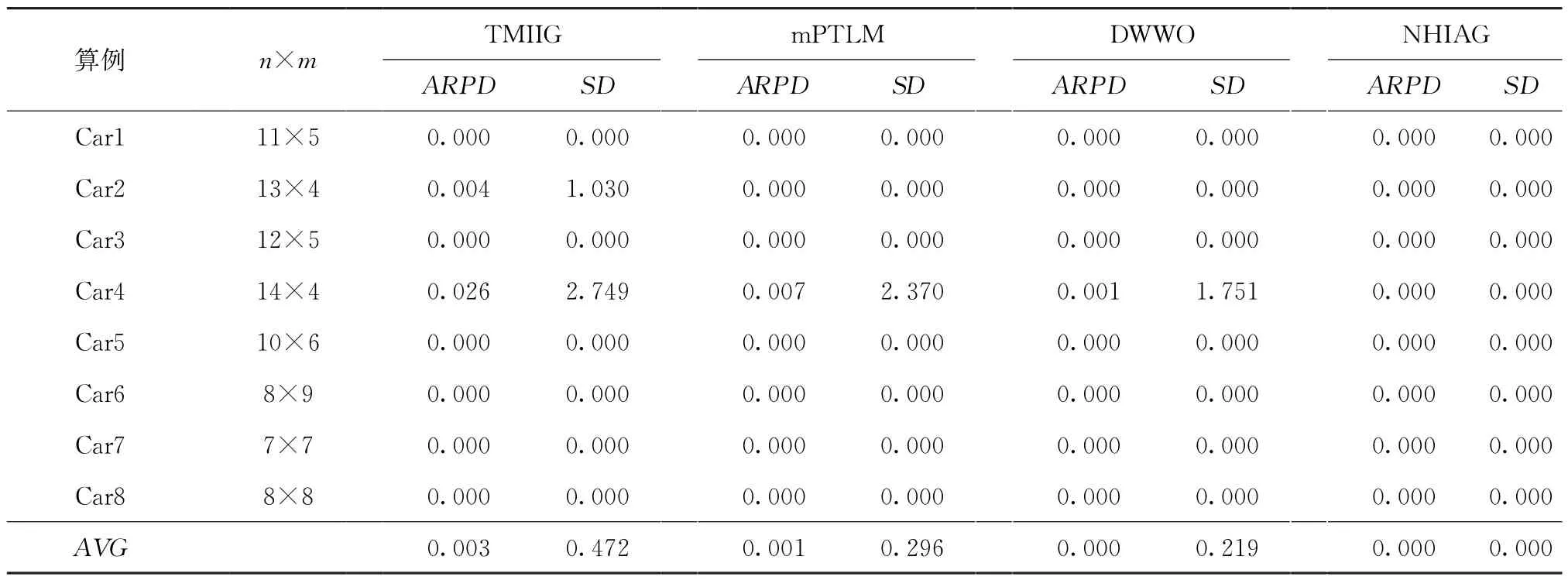
表2 Carlier基准算例测试结果比较

如表3所示为算法求解Reeves算例运行结果。从表格中可以看出，在工件规模数n=20时，NHIGA与其他算法求解结果基本一致，但其他较大规模的问题，NHIGA 的求解质量优于其他3种算法的求解质量。从总体上看，NHIGA 所求ARPD 的平均值为0.06，明显优于TWMIIG、mPTLM 和DWWO 三种算法求得的0.11、0.08、0.07，这表明NHIGA算法在求解较大规模的NWFSP问题时，其算法计算精度依然更优。从NHIGA 所求的标准偏差SD的平均值也可以看出，通过NHIGA求得的结果离散程度较小，表明NHIGA的稳定性能更优。

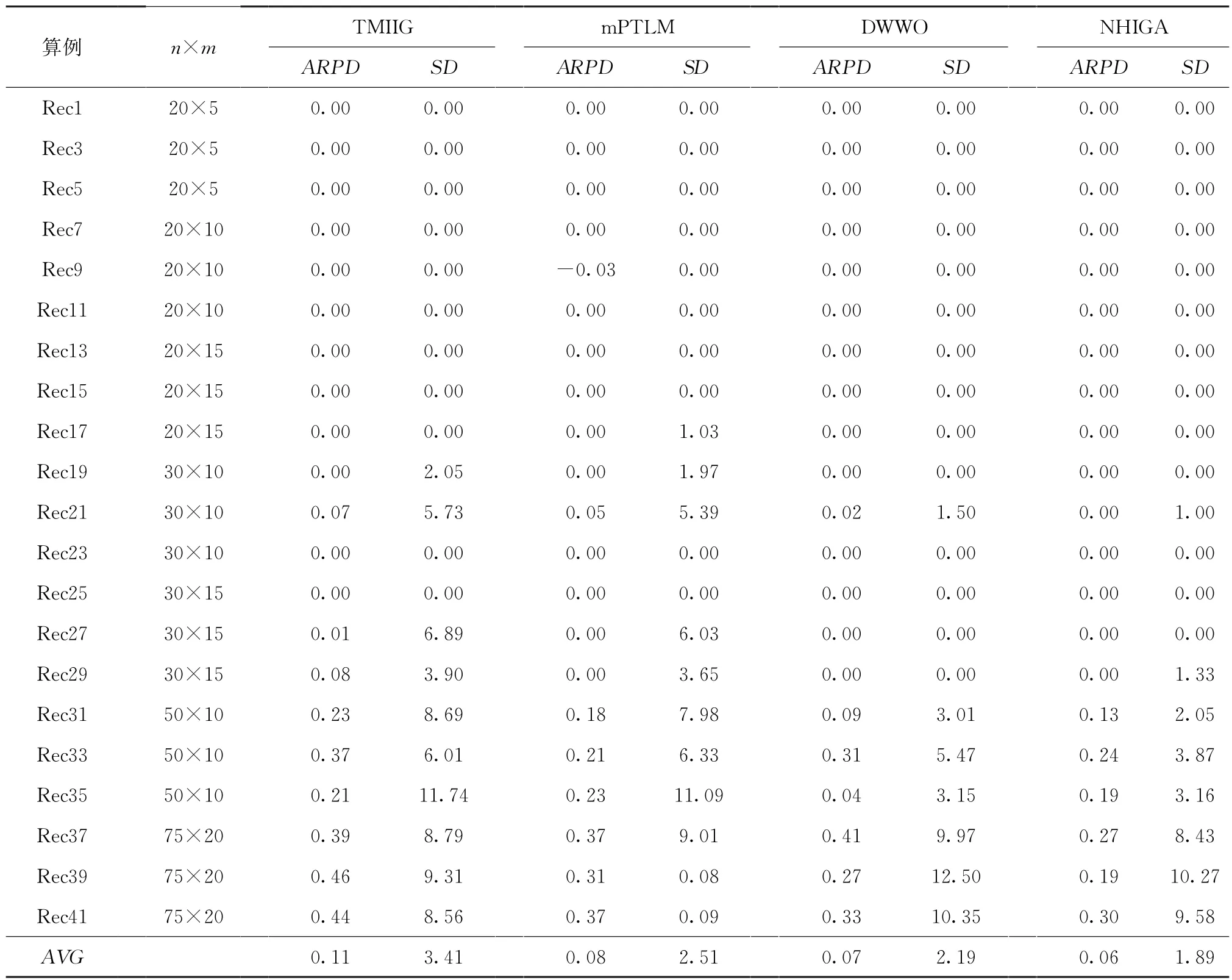
表3 Reeves基准算例测试结果比较

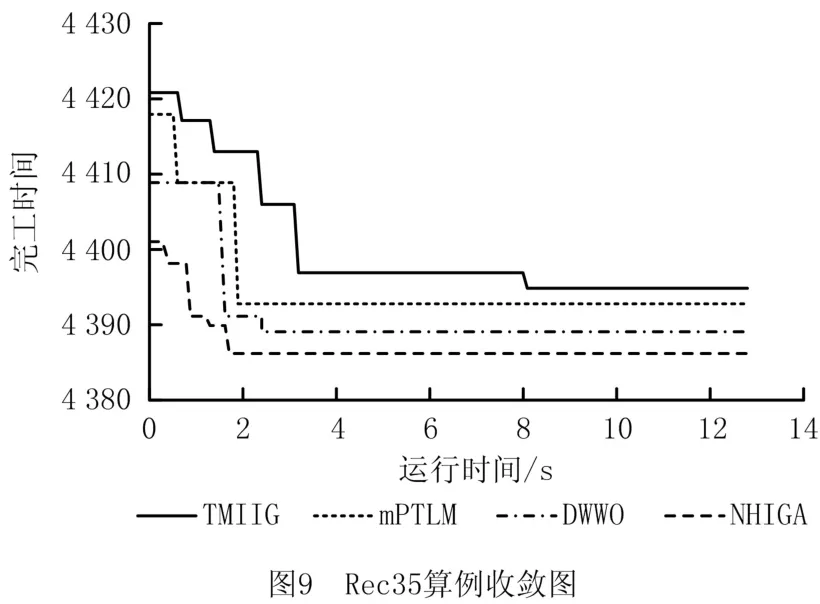
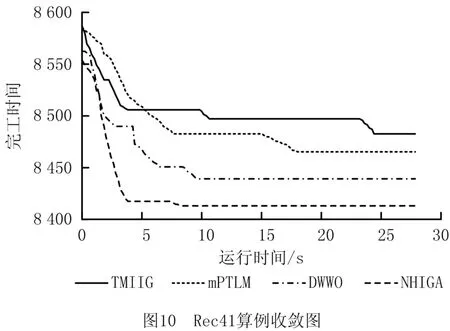
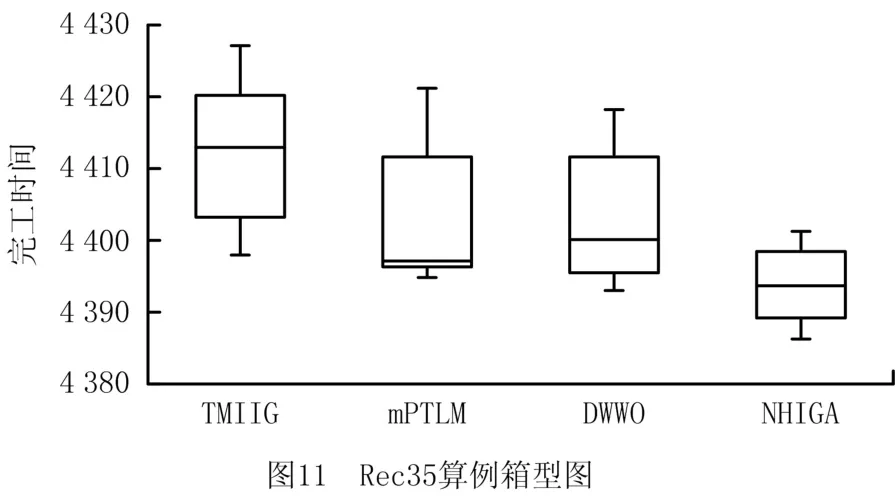
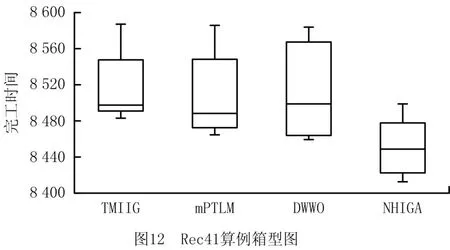
图9和图10 展示了NHIGA 算法求解算例Rec35和Rec41时与其他3种算法的收敛曲线对比图。图9和图10表明NHIGA 的收敛速率和求解精确度均优于其他3种算法。图11与图12展示了4种算法在求解算例Rec35和Rec41时所得数据的箱型图，箱型图可以直接反应测试数据的离散程度，进而可以判断算法的稳定性。图11与图12进一步验证了NHIGA 在求解NWFSP 问题时，相比TWMIIG、mPTLM 算法和DWWO 算法具有较好的稳定性。

为进一步证明NHIGA算法在求解大规模问题时的优越性，本文测试了Taillard算例。如表4所示，对于大规模问题的求解，NHIGA 算法与其他3种算法相比，其计算精度依然更高。在求解算例Ta100、算例Ta110和算例Ta120时，NHIGA 求得的ARPD值均小于其他3种算法得到的ARPD值，这表明NHIGA 在求解大规模问题时仍然具有较好的求解性能。此外，SD值也反映了NHIGA 算法在求解大规模问题中的稳定性。

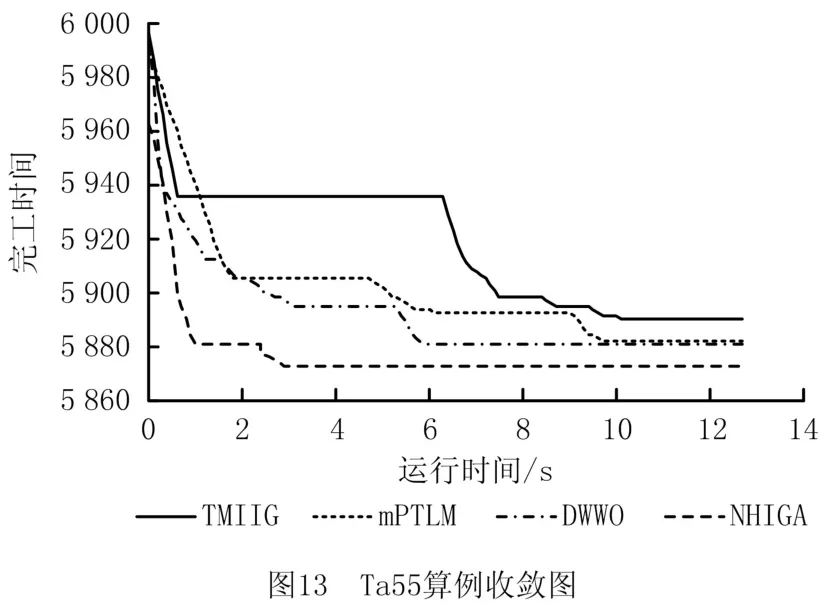
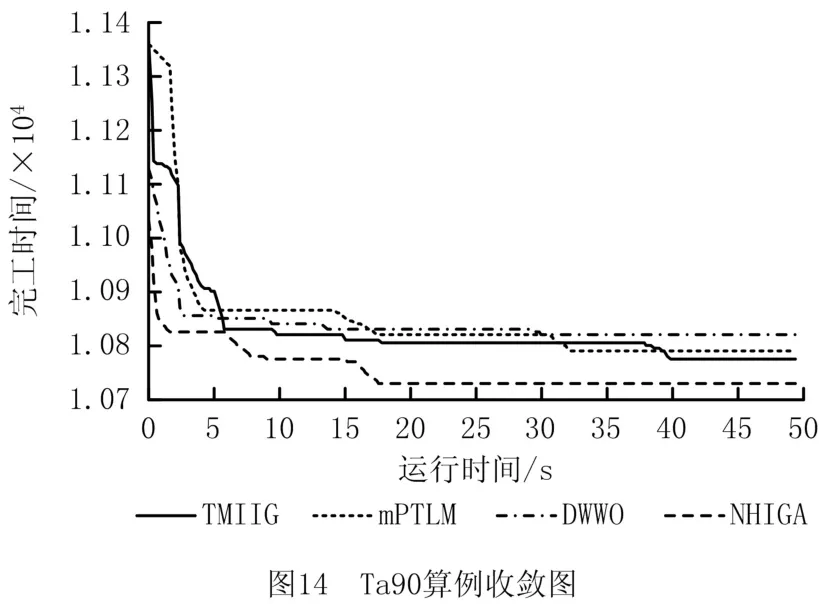
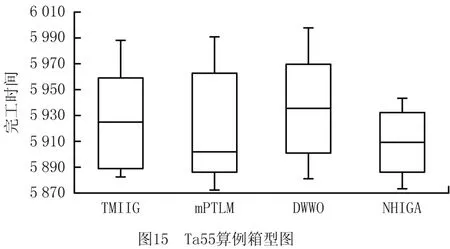
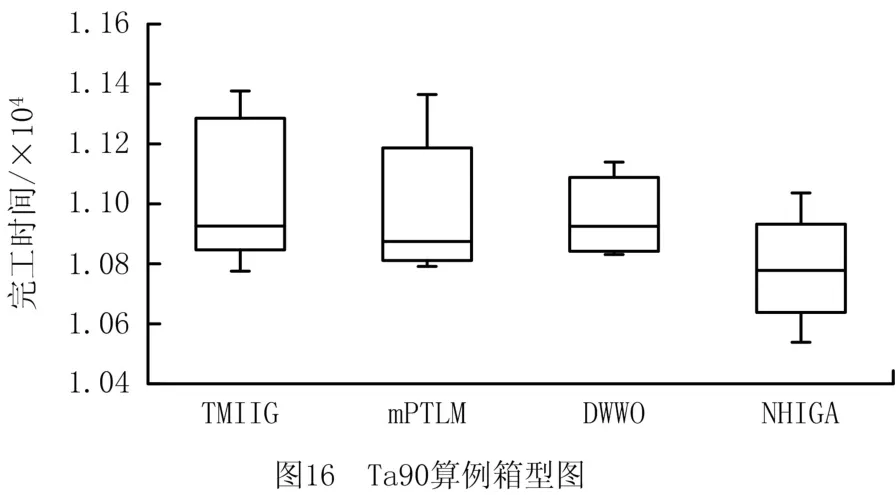
实验过程还展示了算法求解算例Ta55和算例Ta90的收敛曲线对比图，如图13和图14所示。收敛图证明了NHIGA 算法收敛速度更快，寻优能力更强，能够求得更优的结果。图15和图16显示了求解算例Ta55和算例Ta90时所得数据结果的箱型图，该图进一步说明了本文所提算法在求解较大规模的问题时仍然具有较好的稳定性。由于所有算法的运行环境是相同的，由此可以说明NHIGA 比其他算法的求解性能更优。

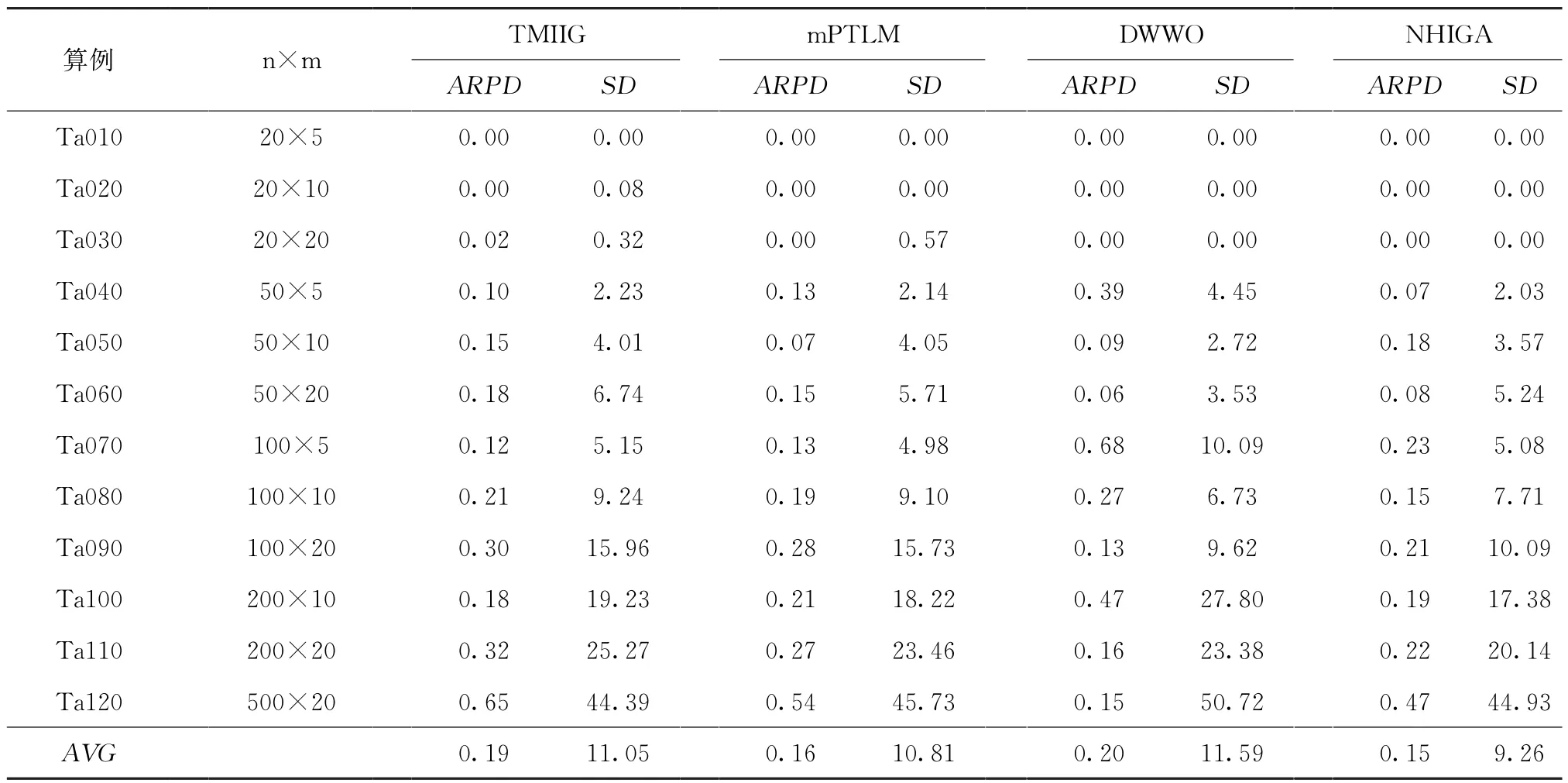
表4 Taillard基准算例测试结果比较

4 结束语

本文以最小化完工时间为优化目标，根据零等待流水车间调度问题的特点，提出了新型混合改进遗传算法。初始化过程采用改进NEH 算法形成具有较高质量的初始种群;在算法计算过程中设计了基于关联规则的数据挖掘方法，寻找优势染色体上的优势基因，并将优势基因组成优势块，借助优势块实现基因重组，从而达到降低问题复杂度、加快算法求解效率的目的;算法交叉过程设计了3种交叉方式，有效地提高了算法的交叉性能，从而引导个体向优势个体发展;为提高种群多样性，避免变异的无效性，结合种群分割思想提出了基于众群分割的变异操作，将分割后两个不同质量的子种群赋予不同的变异概率;此外，根据NWFSP的特点提出了基于NEH 的邻域搜索机制，以提升算法的局部搜索能力，进一步提高种群质量和多样性。采用标准算例对算法有效性进行了验证，通过分析计算结果的精度、离散程度和收敛性，表明了本文算法求解NWFSP的可行性和有效性。但是，本研究未对参数的选择进行理论说明，这是下一步需要进行深入研究的地方。同时，NWFSP还存在其他更接近生产实际的约束问题，下一步将对问题进行深入挖掘，研究更加符合生产实际的具有多种约束机制的NWFSP模型。