基于方向选择的移动机器人路径规划方法

吴 铮，陈彦杰，3+，何炳蔚，林立雄，王耀南

(1.福州大学机械工程与自动化学院，福建 福州 350108;2.湖南大学电气与信息工程学院，湖南 长沙 410082;3.机器人视觉感知与控制技术国家工程实验室，湖南 长沙 410082)

0 引言

移动机器人已广泛应用于生产生活的各个方面，如智能物料运输[1]，无人驾驶汽车[2]、服务机器人等。在移动机器人运动过程中，路径规划是实现机器人自主导航的重要组成部分之一。路径规划的主要作用是为机器人提供一条从起始状态到目标状态的连续路径[3]，并满足一些任务需要所设定的性能指标，如时间、距离和能量等。移动机器人通过路径规划能够实现自主探索或扩展于多机协同应用任务[4]。

基于采样的运动规划方法因能为机器人快速地提供路径方案而广受欢迎。其中，概率路线图(Probabilistic Roadmaps，PRM)[5]和快速探索随机树(Rapidly exploring Random Trees，RRT)[6]是具有代表性的两个方法。它们虽然计算效率较高，但是被证明无法提供最优的路径[7]。因此，研究人员在其基础上提出了渐进最优的规划方法，如PRM*和RRT*及变种等[8-10]。其中，快速行进树方法(Fast Marching Tree，FMT*)兼具了PRM*和RRT*的优点，展现出良好的应用前景[11]。但在环境复杂以及需要大量样本来获取最优路径的情况下，FMT*存在冗余探索的现象，导致计算效率低下。为了提高FMT*的探索效率，Starek等[12]提出了双向扩展的FMT*方法(Bidirectional Fast Marching Tree，BFMT*)，它通过交替从起始状态和目标状态进行树扩展来提升效率。但是，BFMT*仍然没有改善树扩展时的低效探索问题，导致冗余探索现象仍存在于扩展过程中。Salzman等[13]通过运动规划下界(Motion Planning using Lower Bounds，MPLB)进行区域分析来排除多余点的探索;相似地，Xu等[14]在FMT*上应用了Informed-RRT*[15]中的收缩椭圆区域思想(Informed Anytime Fast Marching Tree，IAFMT*)，通过空间约束避免了对整个空间的冗余探索。但是，MPLB和IAFMT*的空间约束划分高度依赖于预处理和初始路径的质量，失当的预处理和曲折的初始路径均会导致区域划分不合理和探索效率低下，极端情况下甚至无法找到质量较高的路径。Ichter等[16]使用图形处理器(Graphics Processing Unit，GPU)来处理FMT*的扩展过程(Group Marching Tree，GMT*)，利用GPU 的并行处理能力对扩展样本批量处理提高效率，该方法具有一定的使用门槛，并且与硬件性能高度相关。上述文献大多从预处理或空间局部采样的角度出发进行改进，但在扩展过程中仍对周围所有样本进行广度搜索，计算效率具有一定的提升空间。启发式函数可以对样本的扩展情况进行评估，引导方法进行有目标性的深度探索。Gao等[17]将BFMT*与传统A*方法结合形成双向启发式方法(Heuristic Bidirectional Fast Marching Tree，HBFMT*)，利用启发式函数的代价计算方式，引导样本扩展方向提高方法探索效率。然而，传统启发函数使用的样本信息不够充分，有时会影响计算效率。因此，通过对启发函数进一步改进来改善规划方法的探索性能也成为了研究热点之一[18-19]。

为了解决FMT*在探索过程中由于广度搜索导致的冗余探索问题，本文提出了基于方向选择的快速行进树方法(DS-FMT*)。该方法设计了一种方向选择的新型启发式函数，可根据周围环境情况来构造方向信息，以此来改变样本的代价梯度变化。随后，通过评估样本代价向有利于探索的方向引导，减少了对冗余空间的探索。同时，借鉴了LBTRRT(Lower Bound Tree-RRT)[20]的近似渐进最优性，将规划终止条件设置为最优解的倍以内，实现保证良好规划质量的同时提升计算效率。对于移动机器人的应用，本文选择路径长度作为规划效果的度量指标。最后，通过仿真对比和移动机器人实际实验，验证了所提出的DS-FMT*方法的有效性。

1 问题描述

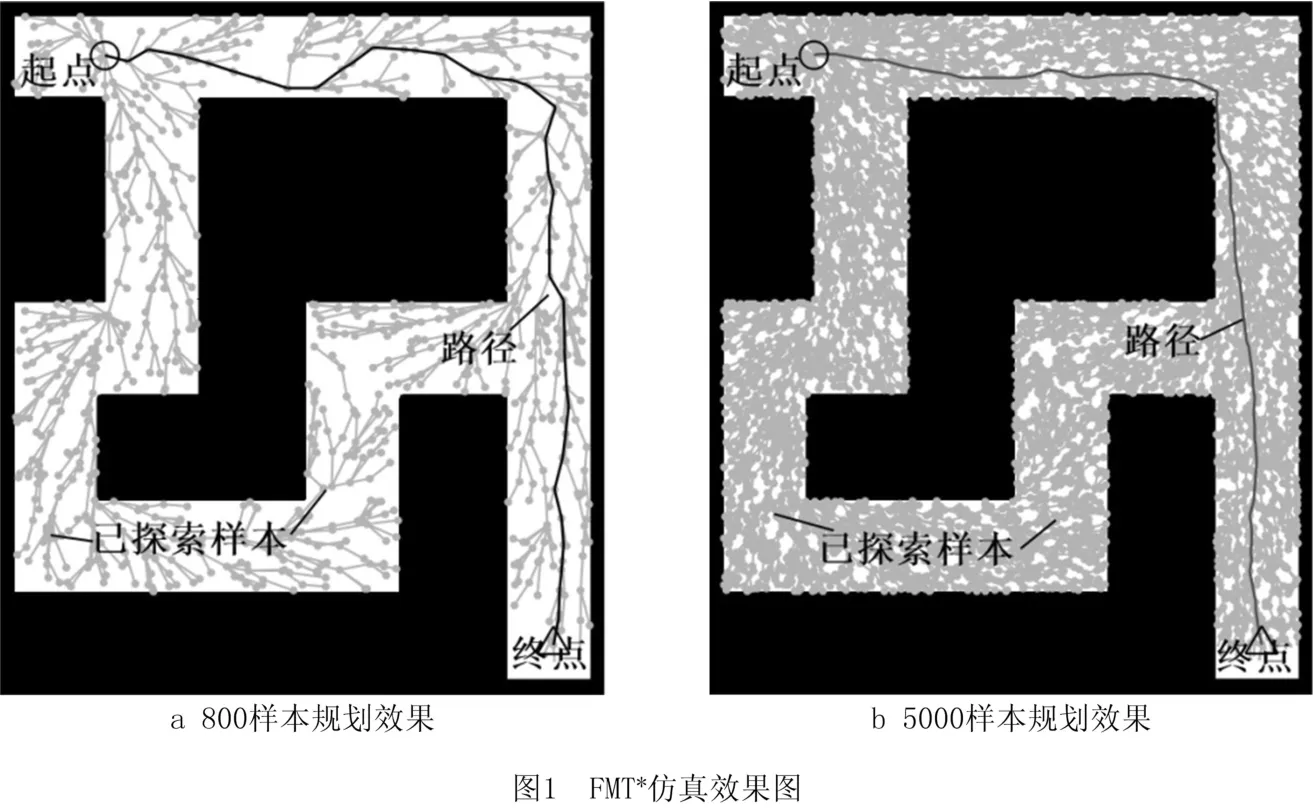
FMT*的递归扩展过程是对整个空间的所有样本进行广度搜索，过多不必要的样本计算会导致规划效率的降低。但是，FMT*的渐进最优性则要求充足的样本数量以确保良好的规划质量。从图1的FMT*仿真结果可以证明，在不同样本数量下，FMT*都对整个空间进行了广度搜索。在图1b中，为了获得良好的规划效果，FMT*需要至少5 000个样本才能获得图示的结果。但是，图中左边空间通道的探索不仅不会提升最终规划效果的质量，还会降低规划方法的计算效率。因此，若能引导样本探索向有利于提升规划效果的方向，将极大地提升规划方法计算效率。

FMT*广度搜索导致的冗余探索问题是因为样本的代价梯度变化平缓，使得方法对代价相近的样本都要进行计算。为了进一步分析FMT*产生冗余探索的原因，将FMT*结合传统启发式函数A*(FMT*-A)进行仿真，获得扩展过程中样本代价变化及其热力图表示。图2 展示2000 样本下的FMT*-A的规划效果，图中左上角为起始位置，右下角为目标位置，各虚线圈表示当前探索过程和对应样本代价变化。在热力图中，不同颜色反映了样本代价的大小，亮黄色表示代价最高，标记为未探索样本;其余根据右侧颜色条对应，深蓝色色表示代价最低，标记为起点。

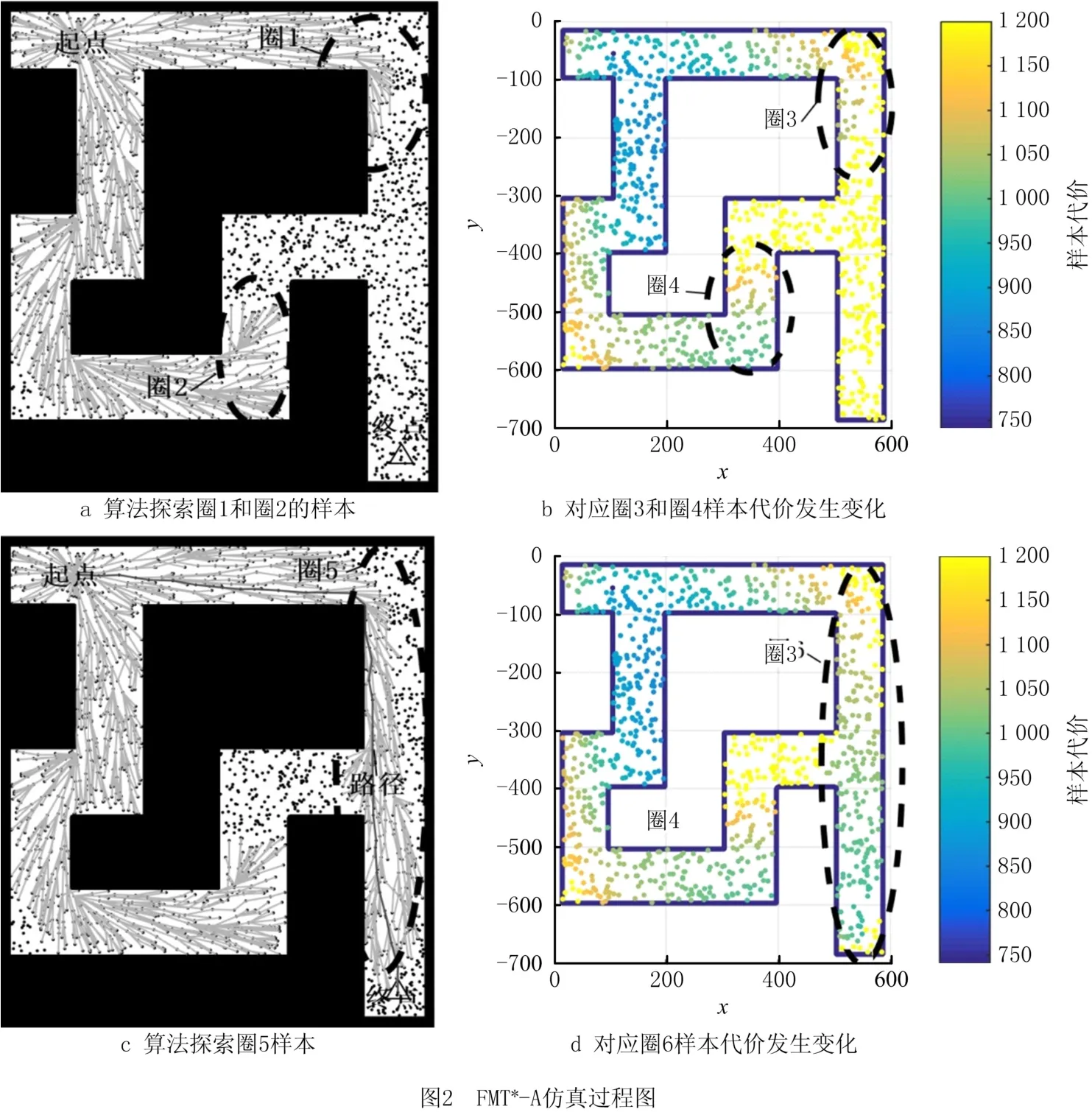
在图2a中，圈2通道分布的样本不会提升方法的规划质量且消耗大量的计算量，但FMT*-A探索了该通道样本。原因如图2b所示，由圈3和圈4中的颜色分布可以看出，两边通道的代价变化相近，造成FMT*-A 对两边通道都进行了探索。在图2c中，FMT*-A通过圈5中的样本最终获得了路径结果，此时FMT*-A探索了整个地图。可以看出地图左侧通道并不影响规划结果却花费了计算时间，表明了FMT*-A规划的样本代价梯度变化平缓导致冗余探索。

综上所述，通过修改样本的代价梯度分布来引导样本的探索方向，可以减少FMT*冗余探索的影响，能够进一步提高FMT*的计算效率。

2 算法构建和分析

为解决上述FMT*存在的问题，本文设计了DS-FMT*算法。本章首先解释了DS-FMT*的整体框架，并改进了FMT*算法的扩展方式。随后对所提方向选择的新启发函数进行阐述，最后对算法进行了理论分析。

2.1 DS-FMT*算法

DS-FMT*算法的整体结构如算法1所示，主要使用以下函数:①SampleFree(n)函数返回一组均匀分布的n个样本;②Near(V，v，r)返回以v为中心，半径为r的范围内的邻居集合。③Expected-Direction(z)如算法2所述，根据周围环境情况返回当前的期望方向向量Ovector。④Find-Orientation(Ovector，xcurrent，xparent)函数将期望方向和当前运动方向综合考虑，最终得到样本的期望方向成本Or(x);⑤F(x)，G(x)，H(x)函数和A*启发函数定义一样:G(x)表示由初始状态到当前点的实际成本，H(x)表示当前点到目标位置的估算成本，通常采用欧几里得直线距离计算，F(x)将两者以及Or(x)结合，综合评价当前样本的代价值;⑥Path函数在算法找到目标点时，根据扩展树的连接情况返回路径解。

算法1DS-FMT*。

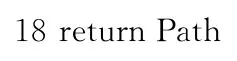
受RRT*方法中样本扩展方式的启发，结合样本代价分布，从计算复杂度的角度来设计DSFMT*扩展结构。考虑到FMT*的递归扩展方式，遍历Xnear中的每个样本都要经过一次Near函数计算和碰撞检测过程，花费的计算数量是O(log(n))，导致遍历完Xnear的操作时间总计为O(nlog(n))。为了降低递归扩展的计算复杂度，舍去Xnear中的Near函数计算，使用样本代价对比进行筛选，

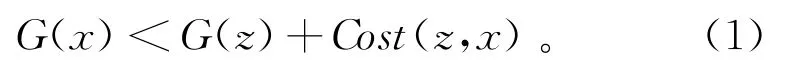
若式(1)成立，从算法1的7～12行和式(1)可得，若Xnear中的样本x代价小于经过当前点z到达该样本的代价，则表明不需要修改样本x的原来代价，可以跳过对x的碰撞检测过程。通过样本代价筛选使得遍历Xnear的计算量降为O(n)，DS-FMT*的计算效率得到改善。

2.2 基于方向选择的启发式函数

为了改变探索中样本的代价梯度来引导探索方向，DS-FMT*设计了一种基于方向选择的启发式函数，可以根据当前样本的环境信息估算样本相应的代价。主要流程如算法2的伪代码所示。

算法2Expected-Direction(z)。

算法2主要返回一个期望的方向向量Ovector，如图3所示。首先给定一个方向集合Pick-Direction(z，L)，以当前点z为中心，向周围发出均匀分布的方向线，并为每条线赋予固定值L。随后，通过以下几种信息的分析综合考虑L的值:

(1)给定布尔函数Is-Unexplored-Area(xvector)，判断该方向xvector是否属于未探索区域方向。若是指向当前点的父节点附近，则将不考虑该方向的后续处理，从而排除一些不必要的方向。

(2)Uncolliding-Length(xvector)函数是对当前点的周围障碍物进行碰撞检测，并返回该方向能够无碰撞的长度M1，作为方向选择的参考信息，该值越大则代表该方向将越偏离障碍物。

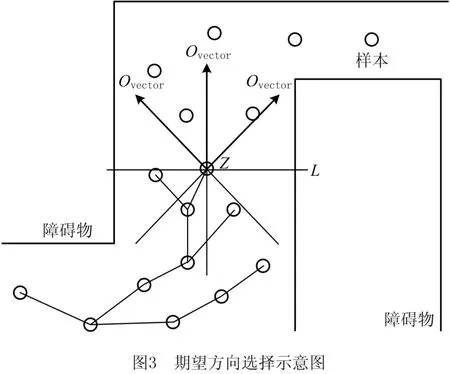
(3)布尔函数Is-Approach-Goal(xvector)判断方向是否指向目标位置，若指向目标则为该方向加权值M2，反之则减去权值。最后综合选取L最大的方向为期望方向向量Ovector。该期望方向将有助于引导DS-FMT*向有利的方向探索。

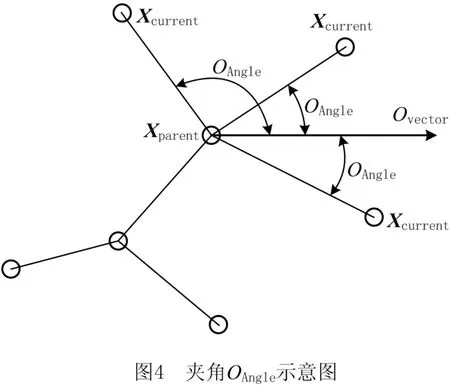
随后引入向量叉积修正法，标记为Find-Orientation(Ovector，xcurrent，xparent)函数，以获得样本在当前探索下与期望方向偏离的计算成本Or(x)。首先计算当前的探索方向和期望方向的偏差，构造两个方向向量，如图4所示。DVector1定义为当前点xcurrent的父节点xparent指向该点的向量，即接下来的实际探索方向，DVector2是由算法2得到的期望方向向量Ovector。将两个方向向量求夹角OAngle，如式(2)所示:

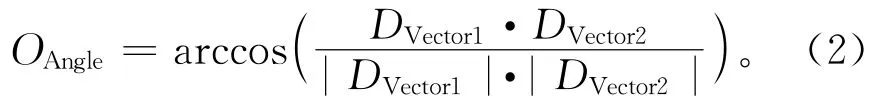
夹角OAngle度量了路径偏离期望方向的程度。通过判断两个方向是否一致，取正负固定值M3，与期望方向偏离小于45°则取正值，然后将M3赋予Or(x)。将Or(x)与当前点到目标的预估成本H(x)结合，二者和的最大值小于单个预估成本H(x)的倍。Or(x)将改变样本整体的代价梯度分布，将有利的样本靠前排序，引导算法更倾向于扩展与期望方向一致的样本，从而减少探索冗余。

2.3 DS-FMT*算法分析

通过DS-FMT*算法的结构和原理，本节为算法提供了相应的理论依据。

定理1概率完备性。给定一个路径规划问题，若问题存在解，则当算法的迭代次数无穷大时，找到可行解的概率为1，即

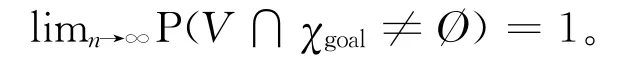
证明 基于以下几个依据:DS-FMT*最终生成一棵连续的树，当一个未知样本被探测时，它将与树中的样本相连。树的根部是从初始状态开始生长的，而目标位置存在于采样样本集合中。当规划问题存在解时，则目标位置将被算法探测到，意味着在树中存在一条可行路径，它连接着初始状态和目标位置。因此，当样本数均匀覆盖所有空间时，树找到一个可行解的概率接近1。基于上述论点，表明DSFMT*算法具备概率完备性。

定理2近似渐进最优性。令(χfree，xinit，χgoal)是d维空间中的路径规划问题。令σ*表示最优路径，c*表示其长度。cn表示DS-FMT*在n个样本下返回的路径长度，且算法需要满足式(3)半径:

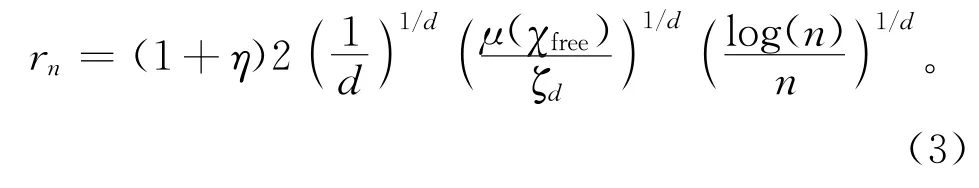
式中:η为正常数，d表示空间维数，μ(χfree)表示无障碍空间的勒贝格测度(即体积或面积)，ζd表示在d维欧几里得空间中单位球的体积。则当样本趋于无穷时，DS-FMT*找到倍最优解的概率为1，即

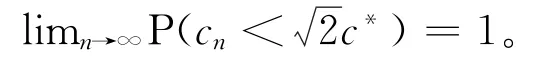
证明DS-FMT*算法基于FMT*结构建立，当无方向信息时启发式函数等于标准的A*算法。通过Likhachev 等[18]进行的论证，当H(x)≤ωH*(x)时，可以使得算法找到最优解的ω倍，其中H*(x)表示问题的实际代价。因此，使用可允许的启发式方法得到的解决方案保证是有界的。DSFMT*算法采用的Or(x)是小于预估函数H(x)至少倍的值，算法找到的解的长度不大于最优解长度的倍。因此，DS-FMT*算法可以得到近似渐进最优的性能。

定理3计算复杂度。考虑路径规划问题(χfree，xinit，χgoal)，样本数为n，则计算一个解会占用O(nlog(n))的时间。同时，DS-FMT*算法会占用O(nlog(n))个空间。

证明由于DS-FMT*是基于FMT*算法的结构建立，调用代价函数的次数是O(nlog(n))，碰撞检测次数为O(n)。对求取邻居点集也是考虑O(nlog(n))时间复杂度。DS-FMT*算法将FMT*算法中对Ynear的计算用重布线方式替代，其复杂度从O(nlog(n))降为O(n)。对启发式函数的构建过程复杂度为O(n)，算法中其他部分复杂度均小于等于O(nlog(n))。根据大O法则，DS-FMT*的计算复杂度为O(nlog(n))。由于算法是边构建图边查询的，没有独立的构图和查询阶段，DS-FMT*具有O(nlog(n))空间复杂性。

3 仿真及结果分析

3.1 DS-FMT*原理对比

为了表示DS-FMT*算法通过方向选择函数达到修改样本代价梯度分布的目的，从而引导样本的探索方向和减少冗余探索的效果。将DS-FMT*与图2的FMT*-A在相同环境下使用不同样本数进行仿真对比，每个样本数进行5次仿真并将数据取平均值汇总在表1中。DS-FMT*的样本代价变化同样使用热力图表示。图5展示2000样本下DSFMT*方法的扩展过程图和相对应的样本代价变化图，图中左上角为起始位置，右下角为目标位置，各虚线圈表示当前探索过程和对应样本代价变化。

从图5可以得到，由于图5b的圈4样本代价高于圈3样本代价，导致DS-FMT*不再扩展图5a的圈2部分，只扩展圈1中方向。因此，图5c中圈5将直接扩展至目标，对应图5d圈6中的代价值逐渐递减，表明该区域一直优先扩展。从图5c可以表明，DS-FMT*有效减少了探索冗余现象。

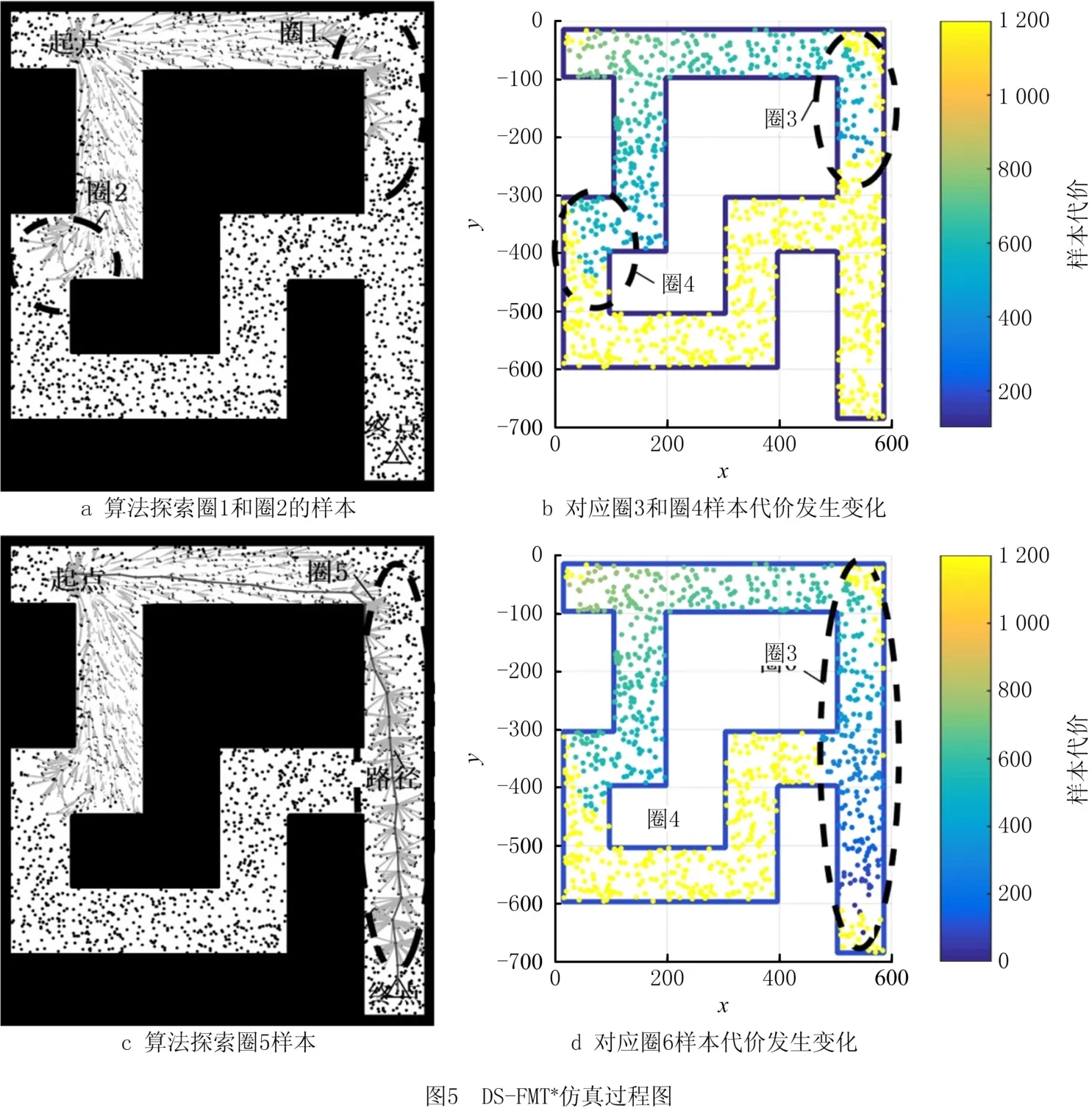
将图5中的数据用表1表示，结合上述对算法的样本变化分析可得，DS-FMT*通过改变原来的代价梯度分布，在同等样本数下，使得探索的样本数比FMT*算法少了至少一倍。从表1的时间对比可得，DS-FMT*比FMT*算法快了3，4倍左右，意味着探索样本数的减少可以提升计算效率。另外，DS-FMT*的路径质量与FMT*所得解的比值大约在1.01左右，保持了良好的路径质量。综上分析可得DS-FMT*通过有效地改变样本代价梯度，减少了冗余探索次数。

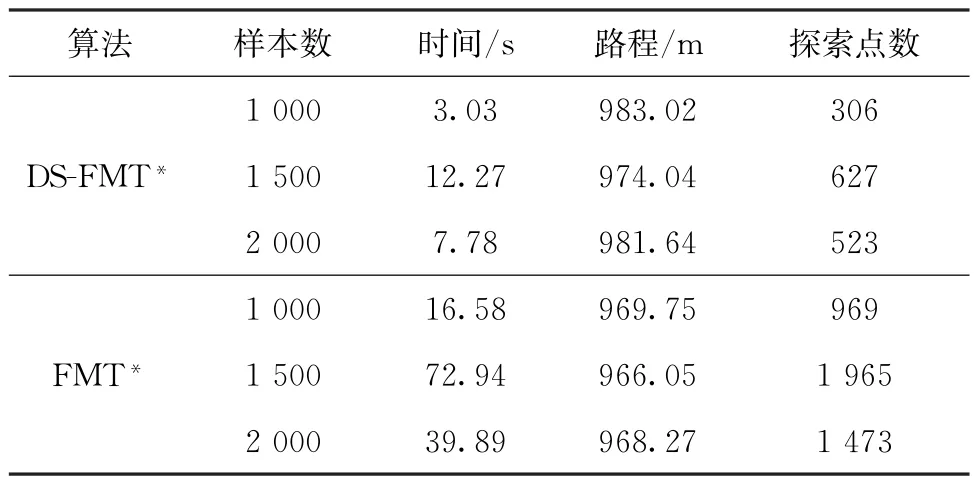
表1 仿真结果

3.2 仿真对比实验

为进一步验证所提算法在效率上体现的快速性，将DS-FMT*算法分别与先进的算法(即FMT*、PRM*、RRT*算法)在各种场景中进行模拟仿真对比。为了确保仿真的有效性，每个环境均采用3种样本数进行仿真。算法基于MATLAB R2016b编写和仿真，采用的计算机配置为:Windows 10操作系统，处理器为i7-6700HQ，运行内存为8 G。

对于所比较的算法而言，DS-FMT*与FMT*、RRT*和PRM*都使用了完全相同的子函数(例如，最近邻搜索、碰撞检查、数据处理等)来确保对比过程的公平。对于每个问题设置，这些仿真以10组为单位，在每组中运行相同数量的样本，最终结果取平均值。样本大小表示搜索树RRT*的迭代数，以及路线图DS-FMT*和FMT*、PRM*的自由空间样本数。对于给定的算法，只有在至少50%成功地找到可行的解决方案时，才记录为给定样本数的一组模拟数据。

地图环境如图6所示，MAP 1～MAP 4均为静态地图。起始状态和终止位置如图中所示，图中展示了最大样本数下各算法的路径效果。MAP 1地图展示了两种长度不同的路径通道，需要算法辨别最优路径所在区域;MAP 2需要算法在多个障碍物中找到路径;MAP 3属于采样算法的经典陷阱问题，需要算法快速找到路径逃离陷阱。MAP 4是迷宫环境，是路径规划的一个典型参照。

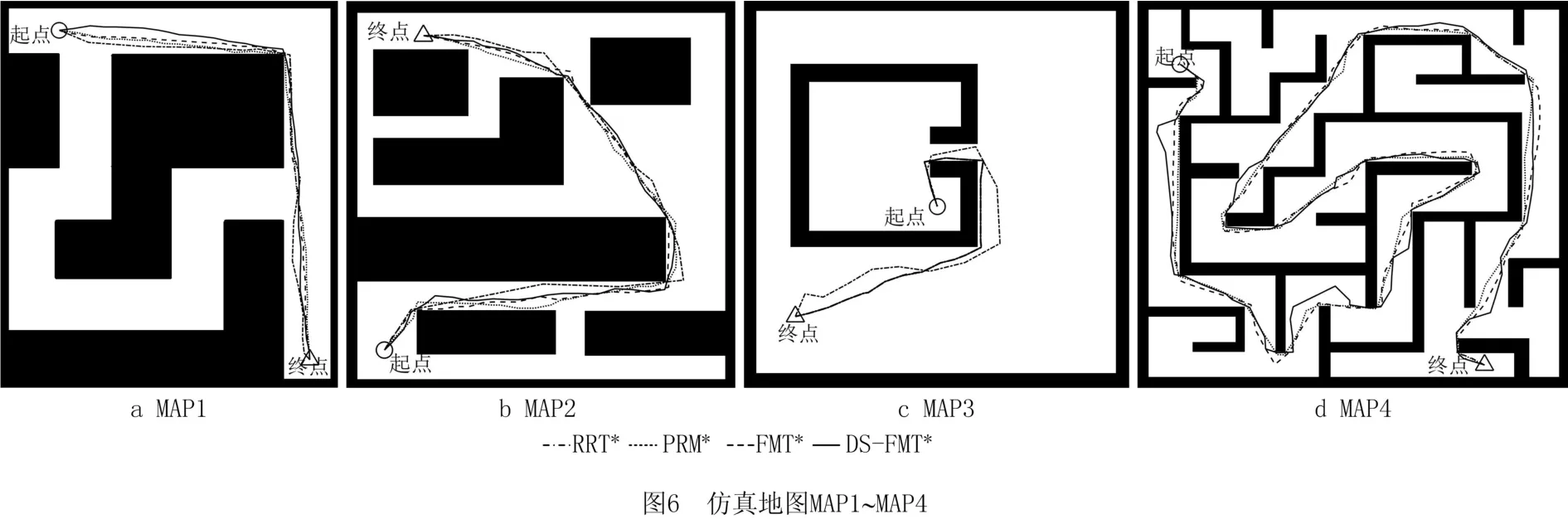
从图6的MAP1可以看出，各方法都能够找到最优路径所在区域。从表2数据可以看出，在不同样本数下，DS-FMT*所消耗的搜索时间均小于其他规划方法，是FMT*和PRM*计算速度的4～5倍，是RRT*速度的2倍左右。而在路径长度方面，FMT*和PRM*获得的路径长度基本一致，并且规划质量最优;DS-FMT*获得的路径长度略差于PRM*，表明DS-FMT*所获规划质量良好。地图MAP2的仿真结果与MAP1类似，各方法均能够在多障碍环境中找到路径，DS-FMT*仍以超过其他方法几倍的速度获得同样质量级别的规划路径，并且，路径质量会随样本数增加而得到改善。

表2 各地图仿真结果

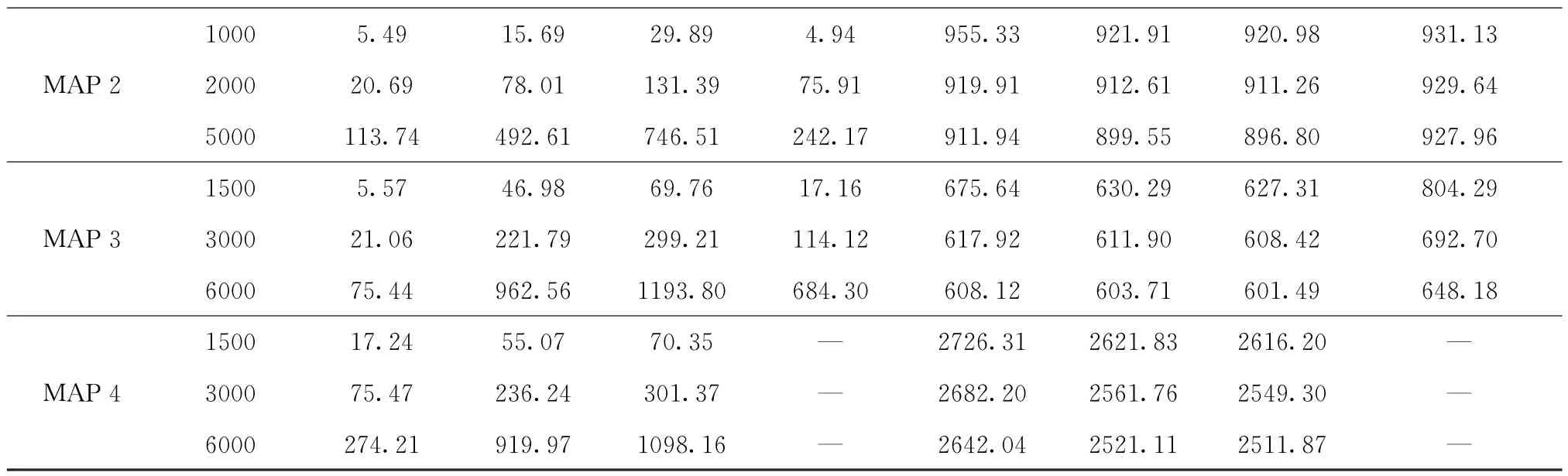
续表2

观察MAP 3可得，DS-FMT*比其他算法效率提高了10倍。虽然在样本数较低时DS-FMT*得到的路径质量较差，但随着样本数的增加，它与PRM*的路径之比接近1.01，说明DS-FMT*的路径质量得到改善，体现了其近似渐进最优性的性能。对于陷阱问题，RRT*需要随机样本恰好位于通道口，才能向外探索，否则会被困于陷阱。因此，RRT*计算效率虽然良好，但改善路径的迭代次数下降，路径长度的平均值高于其他算法。而DSFMT*和FMT*、PRM*等路线图算法基本不受该问题的影响，只要分布足够的样本时，他们都能够成功地扩展，因此数据稳定。MAP 4的迷宫环境情况与MAP 3类似，DS-FMT*和FMT*、PRM*的样本只需均匀覆盖整个地图，就能得到路径解。但RRT*需要超过比其他算法更多的样本数来保证穿过迷宫，成功率不到50%，因此MAP 4仿真不考虑RRT*。通过数据比较，DS-FMT*仍以高效率优于其他两类，路径质量也得到了良好的保证。

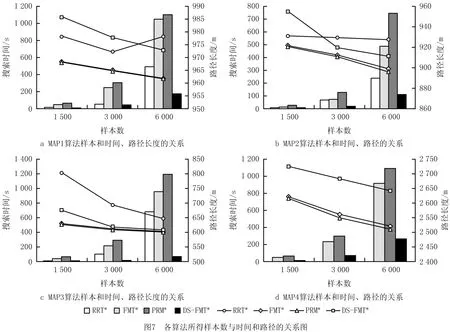
为了进一步分析数据，用柱状图和折线图直观地表示算法的规划趋势。柱状图表示样本数和时间的关系，折线图表示样本数和路径长度的关系。图7a～图7d分别对应4个地图的算法结果。从4个图的柱状图可以看出，FMT*和PRM*的探索时间的增长幅度大于其他算法，而DS-FMT*的增长幅度相对平稳，表明DS-FMT*的运算速度优于其他算法，因为其主要计算速度来自于执行较少的碰撞检查和采样点的探索。从折线图可以综合得出，FMT*和PRM*的路径质量相接近，质量随样本数增加而逐渐改善。DS-FMT*算法的收敛趋势和二者类似，但在路径质量上会存在一定的偏差，意味着DS-FMT*能够找到近似渐进最优解，其解存在一定的上界。对于RRT*，需要足够的迭代次数来改善路径质量，但由于仿真迭代数的限制，RRT*的路径质量低于其他算法。

综上所述，DS-FMT*通过改变扩展方式和采用方向选择的启发式函数，为规划问题提供了良好的路径质量的同时，有效地解决了FMT*的探索冗余问题，提升了FMT*的计算效率。

4 移动机器人实验

4.1 仿真实验

为检验DS-FMT*算法在移动机器人上的应用效果，在ROS操作系统上对移动机器人Turtlebot2进行仿真实验。采用DS-FMT*、FMT*和PRM*算法作为其规划算法，算法基于C++编写，并在rviz可视化界面上显示DS-FMT*的路径规划结果，如图8所示。

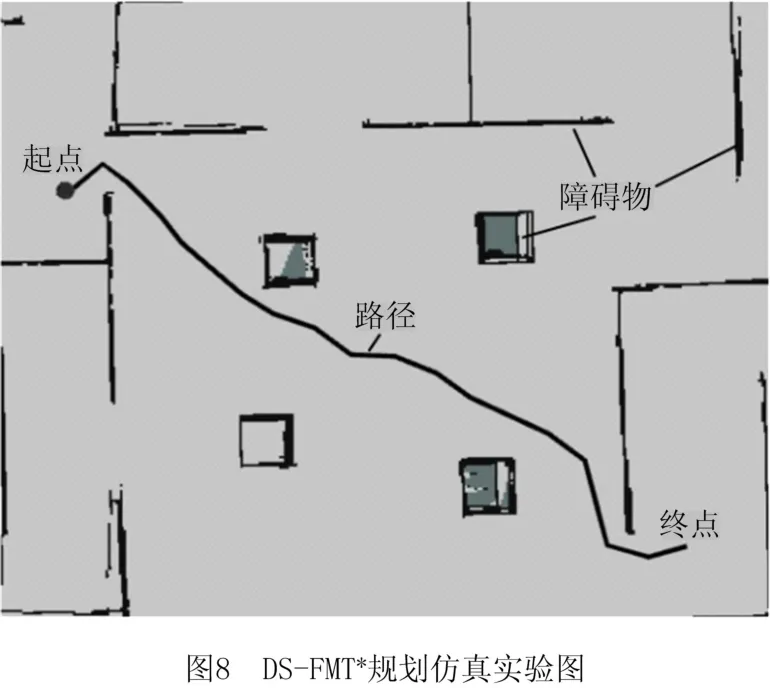
仿真结果如表3所示，使用规划时间、路径长度、探索点数作为衡量算法性能的指标。规划算法均在10 000个采样数下进行规划，共进行10次实验，取平均值进行数据分析。

从仿真结果可以看出，DS-FMT*算法比FMT*和PRM*运行速度快了至少2倍和9倍，探索点数也少了近2倍，表明本文算法有效地通过减少探索的数量来引导算法快速的指向路径;而DSFMT*的路径质量与另外两者质量的比值为1.11和1.09，在当前最优情况下的倍以内，表明所得路径质量良好。这些结果证明了DS-FMT*算法的快速性和近似渐进最优性。

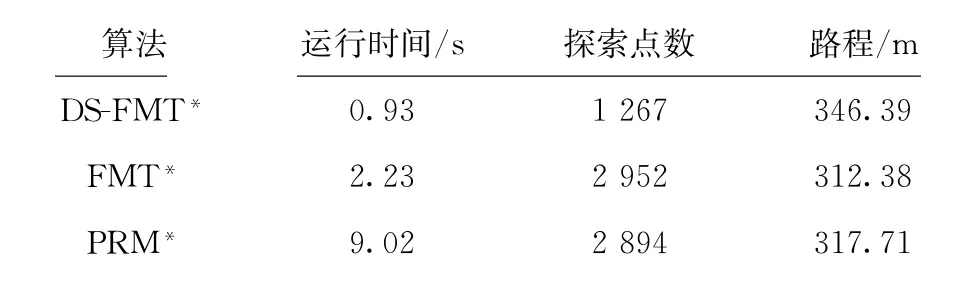
表3 Turtlebot2仿真结果

4.2 实际实验

为进一步证明算法在实际环境下的有效性，在现实场景中进行移动机器人实验。仍使用DSFMT*、FMT*和PRM*算法进行对比。实验场景如图9所示，地图大小为10 m×10 m，机器人Turtlebot2需要从起点移动到目标位置，同时避开障碍物。

各个算法均在10 000个样本分布下进行规划，并进行5次实验，取平均值对数据进行分析，实验结果如表4所示。以运行时间和路程长度作为评价算法性能的标准。由表4各算法的运行时间对比可以看出，DS-FMT*比FMT*和PRM*的运行速度快了至少2倍和6倍，表明了DS-FMT*有效地通过降低计算复杂度来减少运行内存开销。对应DSFMT*的探索点数比其他算法少，说明探索冗余的减少有利于提高算法的计算效率。表4的路程长度表明，DS-FMT*的路径质量在可接受的允许范围内[20]，符合算法的近似渐进最优性。实验结果表明，DS-FMT*算法有效提高了计算效率并能够提供合适的路径方案。

通过仿真和实际实验，证明了本文设计的基于方向选择的启发式函数充分利用了周围环境的信息来合理分布样本的代价梯度，为算法提供了良好的扩展方向，引导算法快速探索到目标位置。所提算法DS-FMT*在性能上具有着良好的表现。

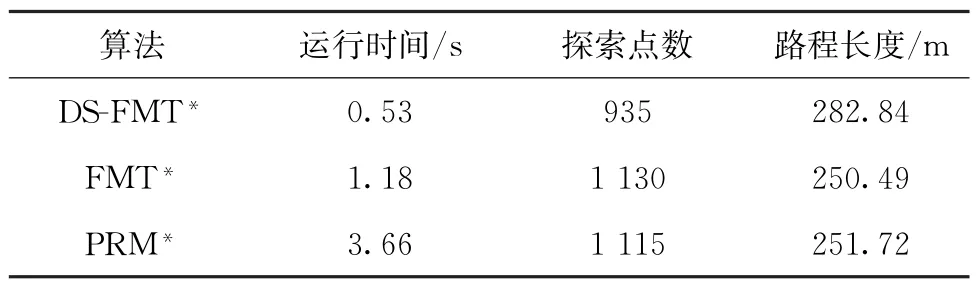
表4 Turtlebot2实验结果

5 结束语

为解决FMT*规划算法存在的探索冗余的缺陷，本文提出一种基于方向选择的启发式策略算法DS-FMT*。该算法改进的扩展方式可以降低计算复杂度，并减少程序运行的内存开销。设计的方向选择启发函数在搜索过程中，有效利用障碍物信息来选择行进方向。通过改变样本代价梯度的分布，引导算法探索并加快了算法的运行速度。算法仿真结果和移动机器人实验表明，DS-FMT*算法具有高效的计算速度和良好的路径质量保证。

未来计划将DS-FMT*扩展到动态环境，同时研究该算法的实时性，包括采样策略、碰撞检测等。另外，考虑到现实机器人的应用范围，将DS-FMT*延伸到高维空间也是一个挑战。