机理与数据融合的螺栓连接松脱预测

2021-04-12王琳涛张先连刘检华孙清超

计算机集成制造系统 2021年3期

王琳涛，张先连，刘检华，孙清超+

(1.大连理工大学机械工程学院，辽宁大连 116024;2.北京理工大学机械与车辆学院，北京 100081)

0 引言

复杂设备往往由大量零部件通过紧固件装配而成，其中螺栓连接由于具有拆卸方便、连接稳定、互换性强等优点，得到了广泛使用。然而，在实际使用中，机械设备需要承受工作载荷以及机械振动，恶劣工作载荷将引起螺栓连接状态变化，使螺栓头部与被连接件之间发生相对转动，从而导致螺栓夹紧力的减小，进而导致连接失效、设备整体性能下降等重大安全问题。因此，实现螺栓松动过程的预测对螺栓连接的防松设计具有重要的指导意义，避免许多安全事故的发生。

国内外研究人员针对螺栓松脱机理模型开展了大量研究，但预测精度与实测数据往往存在较大偏差。早期对于螺栓松动机理的研究集中在轴向载荷的影响，Goodier等[1]对轴向振动载荷下的螺栓松动进行了研究，发现轴向载荷引起的预紧力下降非常有限。随后，Junker[2]提出，横向振动载荷沿斜面方向的分力会加速螺栓的相对转动，更容易引起螺栓松动，并设计了横向振动试验机进行验证。Nassar[3]对螺栓受横向振动载荷的过程建立了简单的数学模型，并分析了主要影响因素，如孔隙、初始预紧力等。在随后的研究中，又通过分析端面力矩、螺纹力矩、螺距力矩三者的作用关系[4]，建立了更加准确详尽的螺栓松脱模型，也是目前得到广泛认同的松脱机理模型。但螺栓松脱是一个存在非线性与不确定性的复杂过程，理论推导的过程中不可避免地需要进行简化，因此难以完成精确预测，仅适合做定性研究。

随着人工智能理论的高速发展，基于数据的建模方法在工业领域得到了广泛的应用[5-8]。如刘志峰等[9]提出利用BP(back propagation)神经网络建立预测特定工况下螺栓残余预紧力的方法，为螺栓防松提供了参考。但在特征选择中，缺少依据且只使用了单一均值作为预测结果，没有考虑松脱过程中螺栓预紧力的分散性和不确定性。为解决这类存在不确定性的问题，高斯过程回归(Gaussian Process Regression，GPR)得到了越来越多的关注[10-14]，该模型基于对贝叶斯理论的扩展，可以同时预测目标的均值与方差，从而更加合理地解决不确定性问题。

机理模型预测精度不高，而数据驱动的模型预测结果准确，但存在可解释性差的问题，因此机理-数据融合的模型[15-17]有望实现螺栓松脱特性的精确预测。这种融合模型既包含了机理模型的可解释性，同时还兼顾了数据模型预测准确的优点[18]。目前，机理与数据模型融合的方法主要有以下几种:利用机理模型引导数据模型进行特征选择[19];利用数据模型对机理模型进行补偿修正[20];建立两部分模型，机理模型的输出作为数据模型的输入[21];使用数据模型预测机理模型的中间未知变量[22]。考虑到现有螺栓松脱机理模型考量了螺栓在受横向载荷时的复杂受力情况以及各种影响因素，能够正确地反映螺栓松动发生的机理，但为了简化分析过程进行了许多理想假设，导致机理模型与实验数据的拟合结果仍有较大区别，不适宜采用后3种机理-数据融合方法，因此以机理模型引导数据驱动模型进行特征选择是针对这一问题更合理的机理-数据融合方法。

为此，以机理模型先验知识为引导，本文提出一种机理与数据融合的螺栓松脱预测模型。首先结合对螺栓松脱机理的研究，利用参数试验法对机理模型中各特征进行敏感度分析并提取关键特征，随后根据关键特征设计相应松脱实验，通过高斯过程回归建立螺栓松脱和特征之间的数据模型。该模型考虑了松脱过程的分散性和非线性等特点，可以预测螺栓预紧力在不同工况下随振动周期的变化以及概率分布，能够更加准确地反映螺栓松脱过程，此外开发了相应的预测软件，为螺栓工程实践中的防松设计提供指导。

1 螺栓松脱机理模型

1.1 螺栓受力分析

当螺栓被拧紧后，螺栓轴线方向共受到3个力矩的作用:螺距扭矩Tp、端面扭矩Tb以及螺纹扭矩Tt。当螺栓受到横向激励载荷时，螺距扭矩Tp与松动方向一致，端面扭矩Tb和螺纹扭矩Tt共同抵抗螺栓松动，螺栓力矩分布如图1所示。

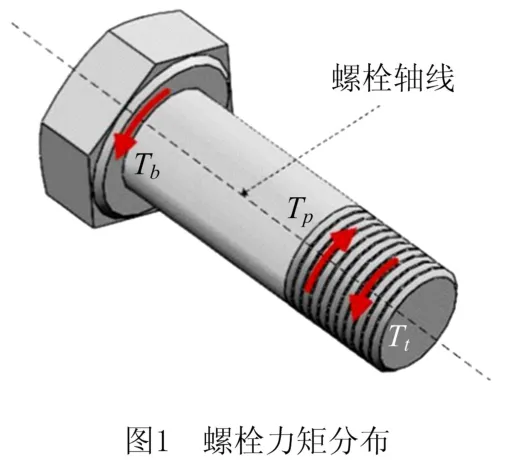
3个力矩共同决定螺栓回转状态:

式中:J表示螺栓转动惯量;ω'o表示螺栓回转加速度。

1.2 螺栓松脱机理模型

根据Nassar等[4]的研究，对于端面扭矩Tb，以ηb为变量建立端面扭矩Tb和端面摩擦剪切力Fbs的函数关系:

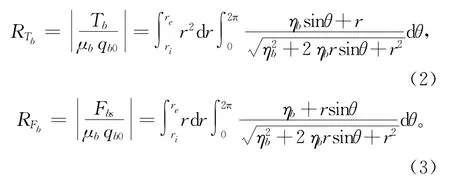
式中:ηb=vb1/ωb表示端面平动速度vb1和端面转动速度ωb的比值;μb表示端面摩擦系数;qb0表示端面平均压强;ri和re分别表示端面接触半径最小值和端面接触半径最大值;RTb和RFb表示连接Tb和Fbs的中间变量。

对于螺纹扭矩Tt，以ηt为变量建立螺纹扭矩Tt和螺纹摩擦切向力Fts的函数关系:

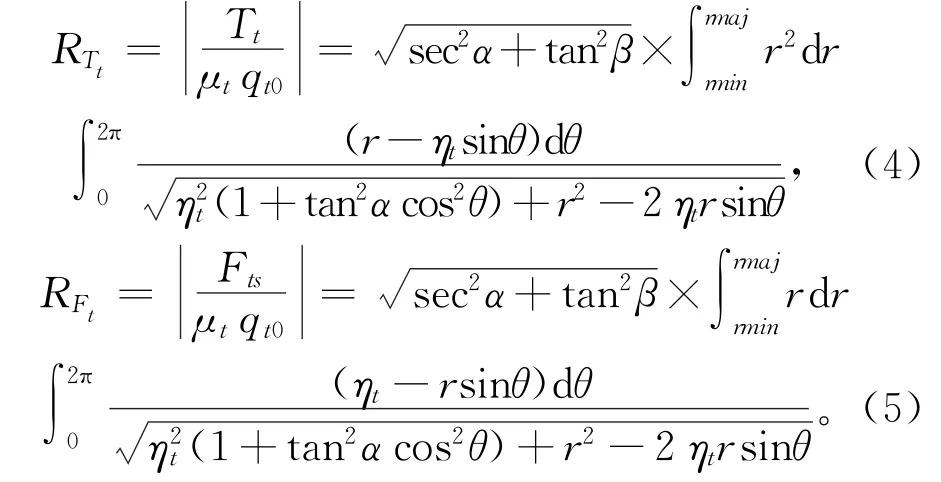
式中:ηt=vt1/ωt表示螺纹平动速度vt1和螺纹转动速度ωt的比值;μt表示螺纹摩擦系数;qt0表示螺纹接触面平均压强;rmin和rmaj分别表示螺纹小径和螺纹大径;α和β分别代表螺纹牙侧角和螺纹导程角;RTt和RFt作为连接Tt和Fts的中间变量。

螺距扭矩

式中:FB表示螺栓夹紧力;P表示螺距。

为简化推导过程，作出如下假设:横向振动位移较小且螺纹上的横向位移xt(t)=0，且横向剪切力不足以克服螺栓头部的静摩擦力，即螺栓头部与上连接件没有发生相对位移，螺栓头部和上连接件共同运动。此时，当螺栓受到横向载荷，螺栓头部横向变形xh(t)为:

式中:E表示螺栓材料弹性模量;I表示螺栓横截面上惯性矩;L表示螺栓有效弯曲长度;k表示螺栓弯曲因子;λ表示一取决于螺栓头部弯曲刚度的计算因子;kb与kc分别表示被连接件刚度与螺栓刚度;ξ表示头部弯曲刚度系数，数值计算结果表明，ξ的减小会提高螺栓防松能力，在本文的研究中，ξ=1。

螺栓头部横向变形量xh(t)与横向振动位移相同，即

式中:δ0表示横向振动幅值;ω1表示激励横向振动频率。

因此，螺栓头部受到的端面摩擦剪切力Fbs由下式给出:

螺纹摩擦切向力Fts由下式给出:

式中τ=rmaj/rmin。

将Fbs、Fts分别代入式(3)和式(5)，可以通过ηt、ηb反求出Tb、Tt。结合式(1)和式(6)可以计算出螺栓头部回转角加速度ω'，并根据下式依次计算得到t+Δt时刻的螺栓头部回转角速度ω以及角位移Δθ。

式中ω0代表t时刻的螺栓回转角速度值。

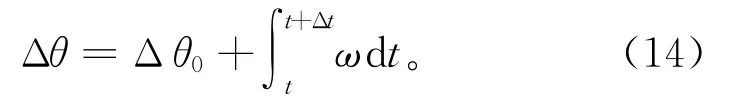
式中Δθ0代表t时刻的螺栓回转角位移值。

当螺栓头部回转角位移为Δθ时，对应的夹紧力下降值

利用上述模型可获得螺栓预紧力随横向振动载荷的时变模型。该模型考虑了螺栓在受横向载荷时的复杂受力情况以及各种影响因素，正确地反映了螺栓松动发生的机理，但为了简化分析过程进行了理想假设，且许多定义的参数可能与实际相差较大，因此机理模型预测结果与试验松脱数据拟合效果较差，如图2所示。

2 螺栓松脱特征敏感性评价

机理模型充分考虑了螺栓受横向载荷时的受力情况以及各种影响因素，尽管难以保证预测精度，但适合做定性研究，因此可以利用机理模型引导数据驱动模型输入特征的选择。从上述推导过程可以看到，螺栓松脱机理模型是一个隐式模型，难以直观的分析各个特征对松脱过程的影响规律，因此，需要通过试验方法对各参数进行敏感度分析。

机理模型中涉及到的特征较多，但其中包括大量标准化的参数。因此，对机理模型特征进行分析筛选后，需要进行特征敏感度分析的特征共6个，表1列出了这6项特征及其变化范围。

表1 敏感度分析特征

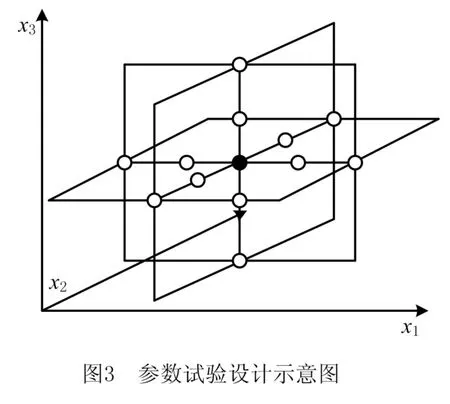
然后利用参数试验法对上述特征在机理模型上进行敏感度分析。参数试验是一种在所有指定水平上独立地变化每个特征，同时其他特征保持原有值的试验方法。通过参数试验可以研究每一个特征对某个响应的敏感性，如图3所示为参数试验的样本分布，其试验次数为:

式中:m表示因子数;ni表示第i个因子的水平数。

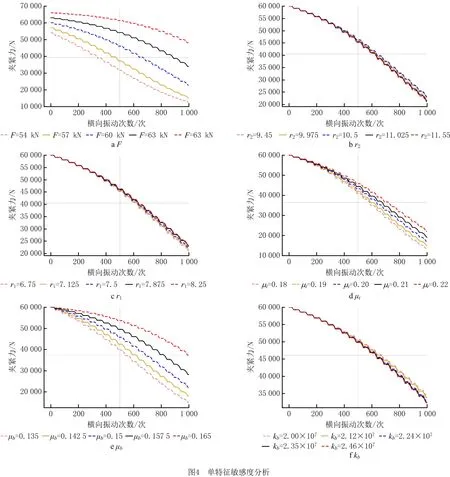
对每个特征在其变化范围内均匀取样5个点，同时保持其他特征为初始值，计算在机理模型中各样本点的松脱曲线，结果如图4所示。

机理模型的计算结果表明，各特征的变化对螺栓松动的影响程度不同。其中，初始预紧力F对螺栓松动影响最为明显，随着初始预紧力的变化，螺栓松动趋势产生了较大程度的变化;此外端面摩擦系数μb对螺栓松动过程也产生了较大影响，而其他特征的影响并不显著。为定量评价螺栓松脱过程对不同特征的敏感程度，本文建立了敏感程度评价指标ε:

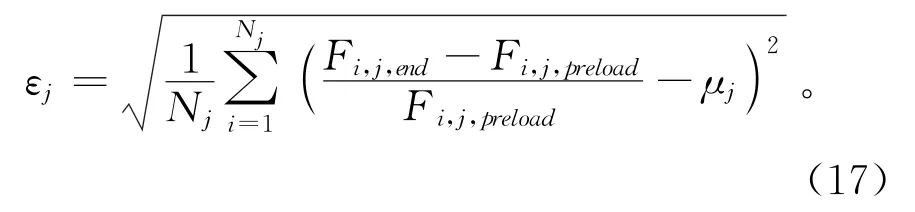
式中:εj表示螺栓松脱对第j个特征的敏感程度指标;Nj表示第j个特征的水平数;Fi，j，end表示第j个特征的第i个水平对应最后时刻的夹紧力;Fi，j，preload表示第j个特征的第i个水平对应的初始预紧力;μj表示第j个特征各个水平夹紧力下降比重的平均值。

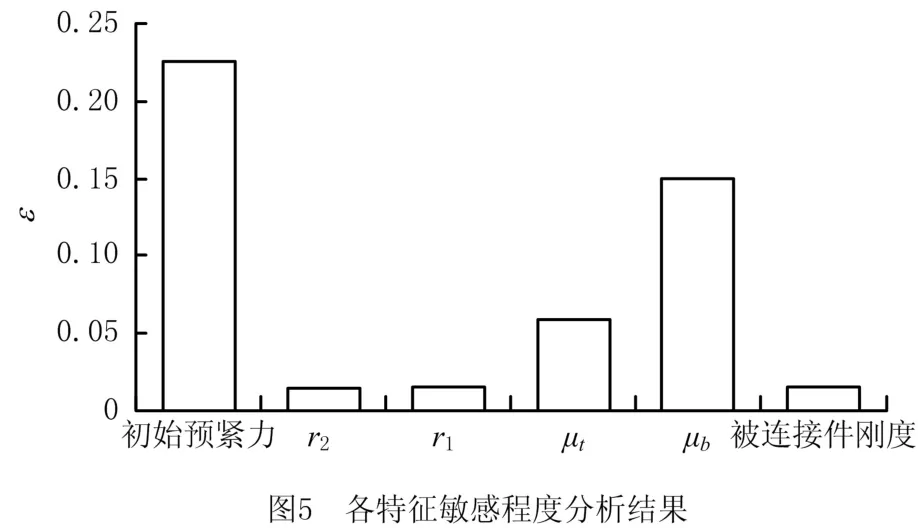
分别对各个特征计算ε，最终得到螺栓松脱对各个特征的敏感程度，如图5所示。可以看到，螺栓松动对初始预紧力、螺纹摩擦系数、端面摩擦系数的变化较为敏感，而对于螺栓头部外径、螺栓头部内径、被连接件刚度的敏感程度较低，因此，最终提取的输入特征为初始预紧力F、螺纹摩擦系数μt、端面摩擦系数μb以及横向振动次数。

3 数据驱动的不确定松脱规律预测模型

3.1 高斯过程回归模型

螺栓连接的松脱具有非线性、不确定性等特点，因此选用高斯过程回归作为数据驱动模型。高斯过程回归是一种基于贝叶斯估计的生成式机器学习方法，可以同时预测目标的均值与方差，对螺栓松脱的分散性和不确定性进行度量，并且能够处理小样本、非线性等复杂回归问题。下面首先介绍高斯过程(Gaussian Processes，GP)，高斯过程是指一个随机过程，其中任意随机变量的有限子集均服从联合高斯分布。对于函数{h(x):x∈R}，若任意有限个变量x1，…，xn，其对应的h(x1)，…，h(xn)均服从下式的概率分布，则{h(x):x∈R}称为高斯过程，可记为h(x)～GP(m(x)，K(x，x'))。

式中:m(x)=E(x)为均值函数，通常为简化起见定义为0;K(x，x')=E[(x-m(x))(x'-m(x'))]为正定的均方差函数。

对于回归问题，通常使用考虑噪声的模型:

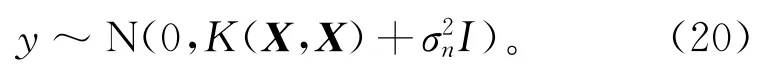
式中X为训练样本矩阵。因此，训练样本y和模型预测值y*的联合先验分布为:

式中:K(X，X)为n×n阶对称正定的协方差矩阵;K(x*，X)为预测值x*与训练样本X之间的协方差矩阵;K(x*，x*)为预测值与自身的协方差矩阵。

在给定预测样本和训练集后，模型预测值y*的后验概率分布为

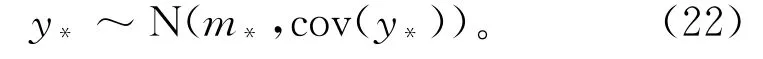
式中m*=K(x*，X) [K(X，X)+]-1y，cov(y*)=K(x*，x*)-K(x*，X)×[K(X，X)+]-1K(X，x*)+。可以看到，高斯过程回归模型不仅可以输出预测结果的均值，还可以输出预测结果的方差，因此可以对预测的不确定性进行度量，预测结果具有概率意义。

高斯过程回归使用高斯过程作为先验，即假设了学习样本是高斯过程的采样，因此协方差函数K(X，X)的选择尤为重要，其描述了学习样本间的相关性。利用高斯过程回归对螺栓松脱数据进行建模就是确定合理的协方差函数，并确定相关超参数。本文中最终采用的协方差函数为平方指数函数，具体形式如下:

3.2 螺栓松脱测试及预测

本节以螺栓松脱实验数据为基础建立高斯过程回归模型。实验数据由横向振动松脱实验台获取，试验台如图6所示主要由移动板、固定板、偏心盘组成，偏心盘将电机的回转运动转化为往复运动，带动固定板形成横向振动，从而引起螺栓松动。本文中涉及到的模型以M14螺栓为例。

根据第2章中特征敏感度分析的结果，本文中涉及到的螺栓松脱模型的输入输出项如表2所示。

表2 螺栓松脱模型的输入与输出

为使模型具有泛化能力，需要控制输入特征的变化来获取充分的实验数据对模型进行训练。其中初始预紧力由超声测预紧力方法控制，分为50 kN、60 kN、70 kN三个水平;螺纹摩擦系数的变化通过对螺纹部分涂胶进行控制，具体数值由标定试验获得;端面摩擦系数通过使用3种不同垫圈或无垫圈进行控制，共分为4个水平，每组试验对应的端面摩擦系数经端面摩擦系数测定试验得到;振动周期通过时间控制，驱动电机工作频率为50 Hz，采集前5 000个振动周期的实验数据进行训练，采样间隔为1 s。每种工况下重复试验3次，取其中2组作为训练集，1组作为测试集，因此训练集共48组数据，测试集共24组数据。

使用试验实测数据的训练集建立高斯过程回归模型，需要确定合适的协方差函数，因此根据模型在测试集上的表现进行选择。如图7所示为分别使用多项式函数、立方函数、平方指数函数、正弦平方函数4种不同协方差函数在初始预紧力为50 kN、端面摩擦系数为0.16、螺纹摩擦系数为0.20工况下的预测结果。可以看到，不同的协方差函数对预测结果会产生较大的影响，为选择预测效果最好的协方差函数，利用在所有测试集上模型预测值与实验数据的平均绝对百分比误差(MAPE)以及均方根误差(RMSE)作为评价不同协方差函数预测表现的指标，计算公式分别为:

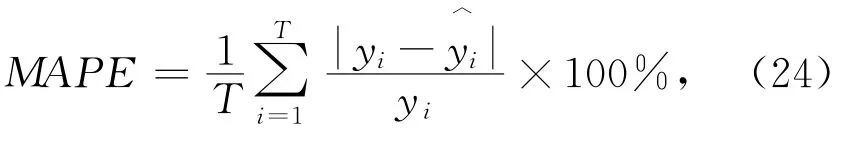
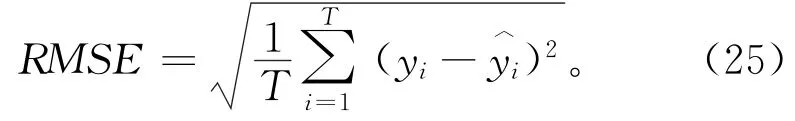
式中，T表示数据点总数量;yi表示第i个数据点螺栓夹紧力的真实值;表示模型在第i个点的预测值。

计算结果如表3所示。可以看出，使用平方指数函数作为协方差函数的模型预测得到的误差最小且趋势较为平滑，取得了更好的表现。从图7中出也可以看到，本文提出的基于高斯过程回归的螺栓松动预测模型输出为一条具有概率意义的分布带而不是一条确定的曲线，与实验数据的吻合程度较好，能够准确地反映螺栓夹紧力变化的趋势，验证了该模型的有效性。

表3 不同协方差函数的预测表现

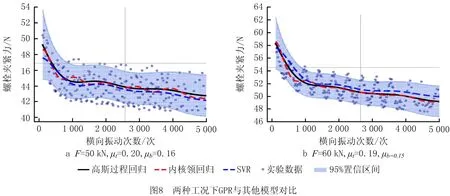
图8给出了在两种不同工况下，高斯过程回归模型预测结果与内核岭回归、支持向量回归(Support Vector Regression，SVR)预测结果的对比。可以看到，高斯过程回归模型获得了与其他模型相似的预测结果，但考虑到螺栓在松脱过程中，螺栓夹紧力并不是一个稳定连续变化的过程，包含了分散性，不能简单地使用一个预测值表征，因此使用高斯过程回归估计螺栓夹紧力在概率意义上的置信区间，能够更加准确地反映螺栓的松脱过程，具有其独特的优势。

3.3 软件工具开发

为提高本文提出的螺栓连接松脱预测方法的工程实用性，笔者采用PyQt5在Eric6环境下开发了相应的螺栓松动预测软件，界面如图9所示。该软件提供了预测给定工况下螺栓预紧力的变化范围以及绘制相应的松脱趋势曲线的功能。此外，还提供了导入新的实验数据的接口，便于对模型重新训练，提高模型对各种工况的适应能力以及预测精度。