三线摆的运动方程、周期及角位置概率分布
2021-04-08吴明珏王顺宇夏雪连章礼华
吴明珏,王顺宇,李 俊,夏雪连,章礼华
(安庆师范大学 数理学院,安徽 安庆 246133)
三线摆主要由水平放置的较小垫盘与较大悬盘,以及对称连接垫盘与悬盘边缘正三角形顶点的三条悬线组成[1].现有不少关于三线摆的研究,如谢淼、吕丹等人的大角度三线摆周期的近似公式[2],王菊香等人的三线摆周期的近似公式[3].常关注的内容有转动惯量的测量、特定状态下的运动微分方程及周期[4],但较少系统性地讨论不同初始摆角情况下三线摆的运动微分方程、周期及角位置概率密度分布情况.本文分别对大摆角及小摆角两种情况进行分析,通过近似处理、积分求解等一系列手段给出了上述两种情况下,三线摆的运动微分方程、周期及位置概率密度分布的分析结果.
1 三线摆的运动微分方程
三线摆结构如图1所示,上、下圆盘的半径分别为r和R,悬线长均为L.将垫盘吊起时,二圆盘面均被调节至水平,两盘间的距离为H,两圆盘心在同一垂直线O1O2上,悬盘可绕中心线O1O2做扭转运动[5,6].
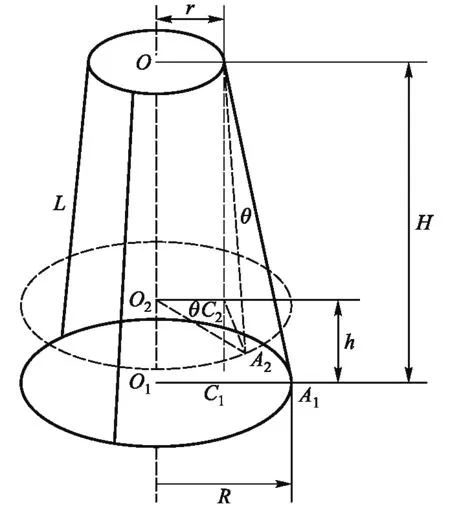
图1 三线摆装置简图
1.1 大摆角情况下三线摆扭转运动的微分方程
当悬盘处于平衡位置时,系统的几何约束为
H2=L2-(R-r)2
(1)
当悬盘角位移为θ时,其垂直高度增加h,在悬线不能伸长的理想状态下,几何约束变为
(H-h)2=L2-(R2+r2-2Rrcosθ)
(2)
由式(1)与式(2)得
2Hh-h2=2Rr(1-cosθ)
(3)
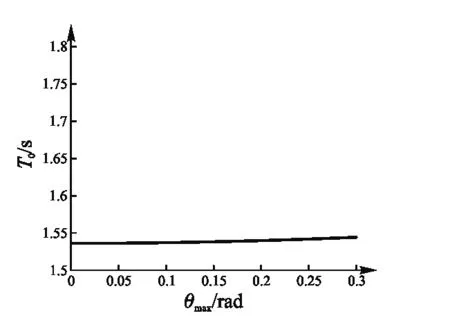
由于实验中下盘上升高度远小于两盘间高度,即可取h< (4) 对式(4)中的时间t求导,得悬盘上下平动的速度为 (5) 在忽略摩擦力及阻力影响的情况下,系统的机械能守恒,由此可利用分析力学中保守系拉格朗日方程进行运动微分方程的求解,可得系统动能中悬盘的转动能与上下平动能,系统动能表示为 (6) 若将自然状态下悬盘高度定义为势能零点,系统势能可表示为 (7) 由式(6)、(7)可得系统的拉格朗日函数为[7] (8) 由保守系统拉格朗日方程 可得三线摆扭转运动在大摆角情况下的运动微分方程,为 (9) 当摆角θmax不超过5°时,习惯上称为小摆角运动,此时可取sinθ≈θ,则式(9)变为 (10) 式(10)为三线摆扭转运动在小摆角情况下的运动微分方程,为非线性方程.但若考虑实验装置的特殊尺寸,则可将式(10)化为线性振动方程,此时三线摆做简谐运动.即若三线摆的几何尺寸中Rr较小于H,即满足[5]: 式(10)描述的运动方程可化简为 (11) 上式为三线摆扭转运动小摆角近似情况下的运动微分方程,具有简谐运动特征. 由于系统机械能守恒,因此悬盘任意时刻的动能与势能之和为常量C,表示为 T+V=C (12) 即有 (13) 其中,由于悬盘上下运动的幅度较小,因此上下平动的动能可忽略不计,得 (14) 由式(14)整理可得[2] (15) 令 (16) 对式(16)两端同时求导得 (17) 将式(16)、(17)代入式(15)中有 (18) 上式为第一类椭圆积分. (19) 上式为三线摆大摆角运动时的周期公式,利用数值计算可以给出三线摆的周期与摆角之间的关系如图2所示(其中物理参数为:H=0.5 m,I=0.0021 kg·m2,m=0.36 kg,R=0.1000 m,r=0.0499 m,g=9.8 N/kg). 总体变化图 周期局部变化图图2 三线摆在不同摆角下的周期 从图2(a)可以看出,随着摆角θmax的增加,三线摆的周期不断变大. 但从图2(b)并结合计算可知,当三线摆的摆角小于0.314 rad(即18°)时,周期曲线近似平行于水平轴,三线摆可视为做固定周期的简谐运动. 三线摆在小角度摆动情况下,式(10)可近似为 (20) 为简谐运动的标准形式.此时,三线摆可看成是做简谐运动.而由简谐运动的相关性质可得 (21) (22) 若记三线摆运动过程中在角位移θ处的瞬时概率为p(θ),即角位置的概率密度函数为p(θ),结合三线摆运动的周期,则有 (23) 其中,dt为角位移θ~dθ对应的时间,T为三线摆运动的周期. (24) 解上述方程得 (25) 将式(19)、(25)代入式(23),再取n=1的近似情况下,可以得到 (26) 为三线摆扭转运动大摆角情况下的位置概率密度函数,其分布规律如图3所示. 图3 摆角 θmax为时的角位置概率分布情况 进一步考虑三线摆做小角度摆动时,由式(22)及式(23)可直接得出小摆角情况下的角位置概率密度函数: (27) 由小摆角情况下的三线摆运动为简谐运动,运动学方程为 θ=θmaxsin(ωt+φ) (28) 将式(21)、(28)带入式(23)进行积分得 (29) 为三线摆扭转运动在小角度情况下的角位置概率密度函数,其中φ由初始值决定. 由式(29)可得三线摆在摆角θmax取0.087 rad(即5°)时的角位置概率密度函数图像如下图4所示. 图4 摆角θmax取0.087rad(即5°)时的角位置概率分布情况 综上所述,本文分析了三线摆在传统意义下大摆角、小摆角下的运动方程、周期,发现在三线摆的固有结构不变时,摆角的变化对周期的影响并不是那么敏感.考虑两种情况下三线摆角位置概率密度函数及分布情况,得出三线摆扭转运动在平衡位置的概率最小,而在最大角位移处的概率最大.因而选择平衡位置作为周期测量计时的始末位置可减少测量误差,这对于提高三线摆周期测量的准确度具有重要的参考意义.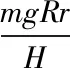
1.2 小摆角情况下三线摆扭转运动的微分方程
2 三线摆的运动周期
2.1 大摆角情况下三线摆扭转运动的周期

2.2 小摆角情况下三线摆扭转运动的周期


3 三线摆运动的角位置概率分布
3.1 大摆角情况下三线摆扭转运动的位置概率密度函数

3.2 小摆角情况下三线摆扭转运动的角位置概率密度函数

4 结束语
