横卧式杨氏模量与组装台秤实验仪的设计
2021-04-08李成龙常芳锦寿化杰沈祺凯
李成龙,常芳锦,寿化杰,沈祺凯
(安徽理工大学 力学与光电物理学院,安徽 淮南 232001)
杨氏模量是描述固体材料抵抗变形能力的重要物理量,是选定机械构件的重要依据之一,是工程技术中常用的参数[1].目前高校大学物理实验中常用静态拉伸法和弯曲法测量杨氏模量.静态拉伸法一般使用光杠杆来放大微小形变量,此方法测得杨氏模量有一定的误差[2].而弯曲法的弛垂度推导公式比较复杂[3],待测物理量较多,实验强度大.本文设计了新的实验方法,能在一定程度上减小实验误差,并将杨氏模量实验拓展成设计性实验.
1 横卧式实验原理
相较于传统的静态拉伸法,新实验仪器将待测钢丝横置,将钢丝两端固定于水平支架上,并使其有一定的初始张力F而绷紧成水平状态.于钢丝中部悬挂钩码下拉钢丝.钢丝受力情况如图1中的横置钢丝的受力分析图所示.

图1 横置钢丝的受力分析图
为了便于计算,设钢丝长度为2L,钢丝中点下移量为Δx(实验中用读数显微镜测得),则由勾股定理可得两侧钢丝的伸长量分别为
(1)
本实验原理的重难点在于计算加砝码后钢丝拉力的变化量ΔF,根据平衡力以及相似三角形,可得到钢丝受到的轴向拉力为
(2)
继续增加砝码则
(3)
设钢丝初始绷紧的张力为F,则
ΔF1=F1-F
(4)
ΔF2=F2-F
(5)
由杨氏模量恒定得
(6)
将式(4)、(5)代入式(6)得初始绷紧张力F为

(7)
再将式(7)代入式(4),即可得添加砝码后钢丝所受轴向拉力的变化量为
(8)
综上所述,由杨氏模量定义公式可得
(9)
此式即为本实验的测量公式,推导过程非常精简,改变两次砝码的质量即可测算出金属丝的杨氏模量.
2 实验测量与台秤设计实验
按公式(9)测相关物理量,测量数据见表1,数据处理中由式(2)、(3)、(7)综合算得金属丝张力F.
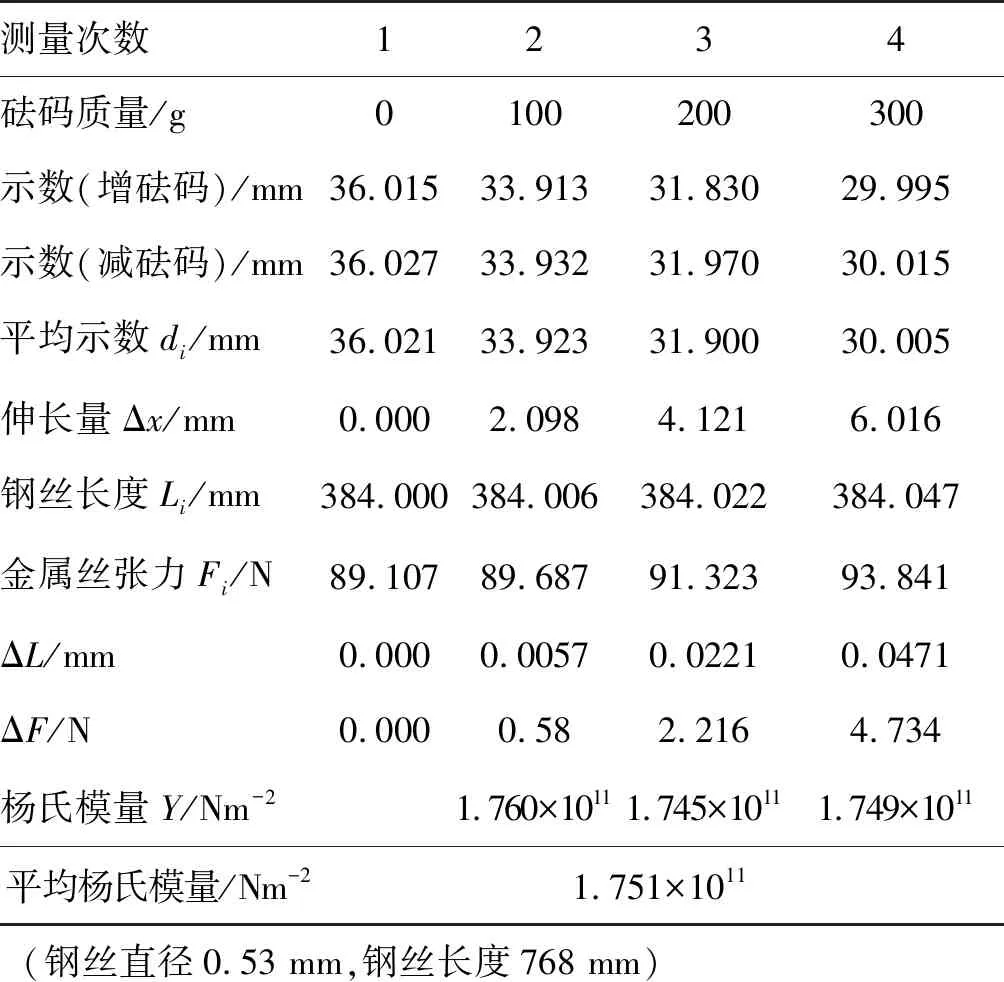
表1 横卧式杨氏模量实验数据与处理
厂家附钢丝标签杨氏模量值1.74×1011N/m2.从本实验设计的推导过程看,本实验结果对数据扰动比较敏感,且从推导公式可知,要提高实验测量精度可增加钢丝长度,用以减小各变化量的相对不确定度,故将钢丝长度增加到近1 m,再测其杨氏模量,实验测量数据见表2.

表2 增加钢丝长度后实验数据与处理

续表
由于实验设计的运算步骤较多,不确定度的传递过程过于复杂,本文采用Crystal Ball[4]模拟估算两次实验结果的标准偏差,以简化不确定度的计算.
在读数显微镜的测量值上附加一个±0.01mm内的均匀分布的随机数,进行模拟估算结果如图2所示.
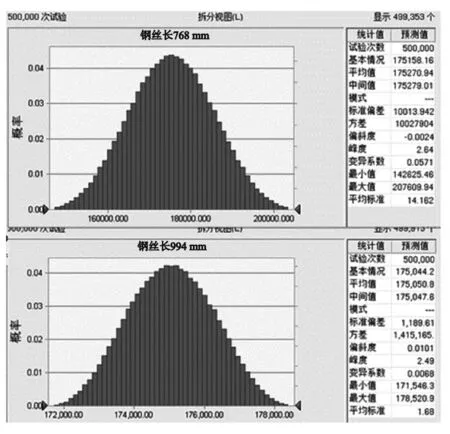
图2 Crystal Ball模拟估算结果
对钢丝长为768 mm的实验测量数据进行模拟估算,其结果偏差较大,标准偏差约1.0×1010N/m2,杨氏模量测量值范围约1.426~2.076×1011N/m2,结果波动较大.而钢丝加长至994 mm实验模拟估算的结果表明,其标准偏差降至接近1.0×109N/m2,杨氏模量测量值范围约为1.715~1.785×1011N/m2,实验结果波动较小、精确度高.
从两组实验数据对比看,增加钢丝长度确实可以提高杨氏模量的测量精度,提高实验装置的稳定性.
横卧式杨氏模量实验装置如图3所示,组装台秤实验装置图如图4所示.基于钢丝杨氏模量的台秤设计实验原理如图5所示,取一段已测出杨氏模量的钢丝,固定于水平支架,并使其有一定的初始张力F而绷紧成水平状态.

图3 横卧式杨氏模量实验

图4 组装台秤测手机重量实验
在钢丝中间位置自由放置一载物台,载物台由连杆圆台和带孔的支架组成,载物台支杆可在支架孔中上下自由运动,载物台连杆下压钢丝,钢丝中点会下移;再在载物台上加载待测物体,钢丝中点继续下移,测量两次下移量Δx,代入计算公式即可算出待测物体重量.
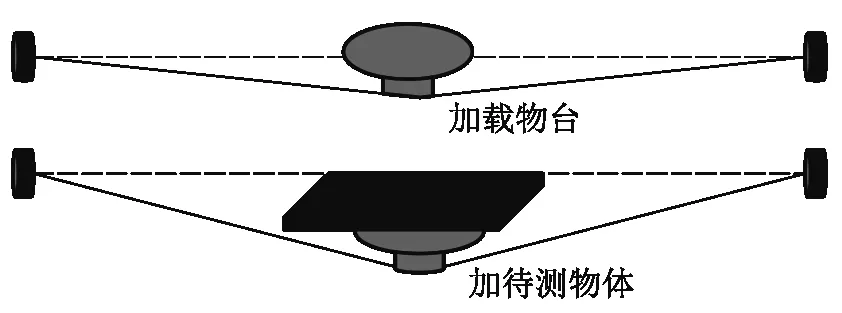
图5 基于钢丝杨氏模量的台秤设计原理
由杨氏模量实验公式(9)逆推并代入公式(4)、(2)可得待测物体重量:
引入公式(4)得
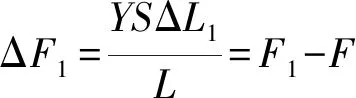
代入式(2)得


表3 组装设计台秤实验测量数据与处理
最终可得手机重量为1.662 N,质量约169.59 g,与厂家标称质量170 g,相差0.41 g,相对误差0.24%.
3 结论
本文设计的横卧式杨氏模量与组装台秤实验装置,经过大量实践证实该装置具有如下优、缺点:
1) 横卧式杨氏模量测量装置,通过对横向绷紧的钢丝进行侧向微小拉伸,从而对拉力产生分解放大,将原来实验需要数千克的砝码,改进为仅需几百克砝码,使实验装置变得精致小巧.
2) 新的实验装置横向位移量Δx,远大于金属丝的伸长ΔL,在一定范围内使得微小伸长量得到比较准确的测量.但由于Δx的变化是非线性的,随着钩码的增加其变化量越来越小,测量误差越来越大.故实验中钩码不宜增加过多,本实验设计只增加3次,且数据处理不适用逐差法.
3) 若钢丝较短实验误差会比较大,实验设计中可通过增加钢丝的长度来提高位移量Δx,从而减小测量的相对不确定度.同时由于钢丝较长,因此钩码受力点的微弧形可忽略不计.
4) 利用Crystal Ball插件进行蒙特卡洛模拟估算标准偏差和其它预测值,有助于高效率的优化实验设计.
5) 该实验装置非常容易反向设计出一款简易台秤.本文推导出该简易台秤的测量公式,并成功用来测定未知物体的重力.此设计将传统的验证性实验项目拓展改进成设计性实验项目,丰富了实验内容.
