器壁旋转模式下液体平衡状态的分析
2021-04-08石立红张俊成潘建澎
雷 奕,石立红,张俊成,潘建澎
(长江大学 石油工程学院,湖北 武汉 430100)
器壁带动液体旋转模型有效综合了流体力学、几何数学、物理光学等多种知识,国内外学者综合这些知识并利用实验得出液体旋转形成的稳定液面为抛物面等大量的研究成果[1-5].器壁旋转液体实验在测重力加速度、液体折射率及液体混合等方面应用广泛[6-10].同时学者对旋转液体的旋转方式、几何关系、衰减特性进行分析总结,更有学者使用VB、fluent等软件对液体旋转实验进行精确的计算、模拟[11-13].但现有的教材、实验、数模仅仅考虑直筒壁下的旋转平衡,并没有指出当器壁斜率发生改变时,一般规律是否依然适用.本文在此基础上引发思考,进一步推导出器壁斜率为K值时的恒等式并研究其参数间的关系,同时利用fluent建立模型,将模拟结果与公式推导相结合,得到的普适性规律,对教学、实验、应用具有指导性的意义.
1 旋转抛物面方程
斜率为K(K≠0)的圆筒容器内盛有一定量液体,容器绕中心轴以角速度W匀速旋转,由于液体粘性的作用,与容器壁接触的液体层会被带动而旋转,使所有液体质点都绕该轴旋转.待运动稳定后,各质点具有相同的角速度,液面形成一个漏斗形的旋转面,如图1所示.以旋转液面最低点为坐标原点O,Ox轴沿水平方向,Oy轴沿中心对称轴向上,建立直角坐标系Oxyz.旋转液体达到稳定状态时,液面切线与水平轴的夹角为θ.液面上质量为m的质元在重力FG和离心力FL的作用下沿切线方向受力平衡,表达式为

图1 旋转自由液面质点受力分析
mgsinθ=mω2xcosθ
(1)
即
tanθ=dy/dx=ω2x/g
(2)
对式(2)进行积分得
(3)
(4)
式(4)证明了,斜率为K的圆筒容器绕中心轴匀角速度旋转时,其自由液面是旋转抛物面,这与直筒壁旋转规律一致.
液面上某一点的斜率K′可表示为
(5)
由式(5)知抛物线的斜率随角速度增大而增大,并且抛物线边缘处(xmax)斜率最大.
2 K的恒等式
盛有液体的圆筒(器壁斜率为K时(K≠0))以一定角速度W绕其中心轴旋转,假设旋转液面最低处恒高于桶底,容器高度足够大,液体不会溢出.各参数如图2所示.由于K值对通式的推导过程没有影响,为方便研究,所以仅研究K>0的情况,进一步探究各参数之间的关系.

图2 斜率为K的容器旋转液体图

(6)
则图2中Oxz坐标平面以上抛物线绕y轴旋转 得到的体积V抛为

(7)
Oxz坐标平面以上高为H的圆台体积VH为
(8)
旋转前Oxz坐标平面上方液体体积Vk为
(9)
由于旋转前后Oxz坐标平面上方液体的体积不变,可得
VH-Vh=V抛
(10)
将式(7)—式(9)代入式(10)化简得
(11)
式(11)即为需要推导出来的恒等式,当旋转容器斜率为K(K≠0)时,r、h、H、K恒满足上述关系式.
3 K的几何特性
3.1 K→∞时的恒等式
当器壁斜率K→∞时,容器变为直筒壁,如图3所示.由式(7)—式(9)得:

图3 斜率K→∞时的容器旋转液体图

(12)
(13)
(14)
由于旋转前后Oxz坐标平面上方液体体积不变,得到
VH-Vh=V抛

(15)
化简得
H=2h
(16)
或
H-h=h
(17)
式(16)、(17)的物理意义为:直筒壁中旋转抛物液面中液位最低点到最高点的距离为最低点到初始液位距离的两倍或液位变化中上升的高度与下降的深度恒相等.文献[12]曾间接得到该结论.
通过式(12)和式(13)得到
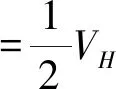
(18)
即旋转抛物体的体积等于同底同高圆柱体体积的一半.这里的结论与文献[2]指出的体积及液位关系一致.
同时由式(17)和(18)得出:当K→∞时,在容器尺寸足够大、初始液位足够高的前提下,随着角速度ω的无限增大,液位的变化是无限的,满足式(17)液位上升的高度恒等于液位下降的深度;体积恒满足式(18),旋转抛物面形成的体积恒等于同底同高圆柱体体积的一半.
3.2 K>0时的临界值
对一般式(11)整理得
(19)
由于K>0、h>0、r>0,因此
(20)

(21)
即
(22)



图4 K=3,ω=50 rad/s,液体正常旋转
通过fluent建立旋转液体层流模型(初始液位30 mm,下底10 mm,上底50 mm,容器高60 mm),给定转速使液体旋转稳定(如图4);增大转速,当抛物面最大斜率K’max>K时,旋转边缘的液体将不再是抛物面,会在离心力和下层液体挤压的共同作用下,沿着斜壁往上增长,形成一层覆盖在斜壁上斜率为K的水膜(如图5),水膜随着转速的增加而生长,此时旋转液体形状分为两部分:1) 容器中部的旋转抛物面;2) 容器边缘覆在斜壁上的水膜,水膜开始出现的临界角速度为ωlj=(gK/xmax)1/2.同时由临界角速度得,角速度越大,xmax越小,即旋转抛物面的范围越小,水膜范围越大.
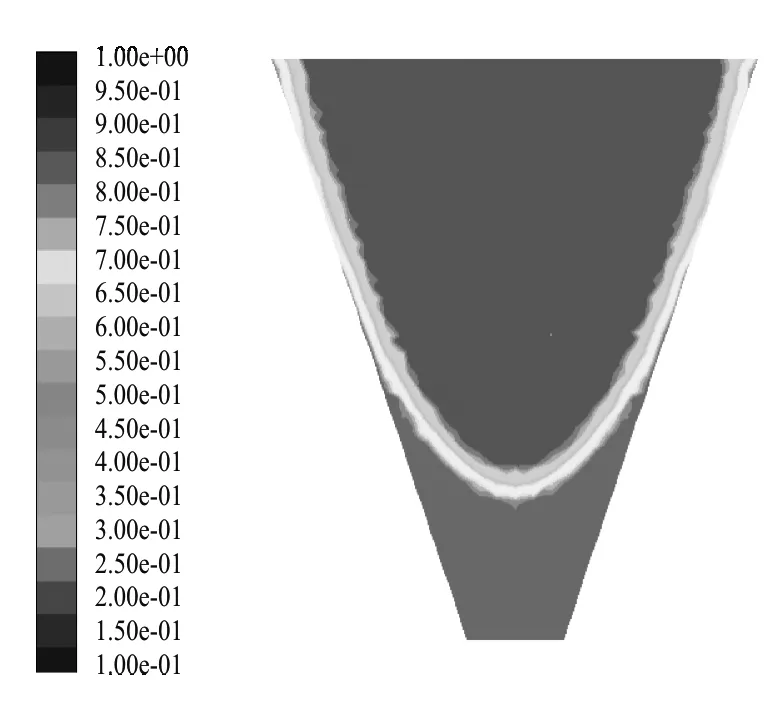
图5 K=3,ω=60 rad/s,形成水膜

4 结论与建议
容器壁带动内部液体旋转形成的平衡液面与器壁斜率K值无关,恒为抛物面,其液位变化、筒内半径、筒壁斜率恒满足等式(11).
斜率K→∞时,容器为直筒壁,随着角速度增加,液位的变化是无限的,但液位上升高度恒等于液位的下降深度,并且旋转液面形成的体积为同底同高圆柱体体积的一半.
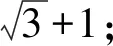
本文没有涉及到器壁斜率K<0时的参数关系及物理意义,其他研究人员可进一步深入讨论.
