一种正三角形结构的双光束干涉装置
2021-04-08周国全
周国全
(武汉大学 物理科学与技术学院,湖北 武汉 430072)
两列或若干列相干光波,频率相同,位相差恒定,振动方向一致,就能在空间相遇时相互叠加,产生光的干涉现象,其表现是在某些区域始终加强,在另一些区域则始终削弱,形成稳定的强弱分布相互间隔的现象. 干涉现象是波动独有的特征. 不同的光学干涉装置就是用不同的方式满足干涉条件[1-11]. 相干光束的产生方式分为波前分割式与振幅分割式;依据干涉光束的数量分类,又分为双光束干涉与多光束干涉;而依据场强与光程差函数的等值变量来分类,则分为等倾干涉与等厚干涉两种类型,例如Michelson干涉仪和Fabry-Perot(F-P)干涉仪. 文献[5-8]论述了若干等厚干涉装置及其变异的干涉结构;文献[9-11]描述了两种分振幅式多光束等倾干涉结构——大顶角等腰劈与矩形腔干涉结构,而一般教科书中的等倾干涉是利用扩展光源照射在厚度不变的薄膜上产生的多光束干涉现象,不同级序的干涉条纹对应不同的倾角. 文献[12-15] 介绍了几种干涉结构的若干应用问题. 本文依据几何光学与波动光学的原理,介绍和分析了一种具有正三角形结构并能产生双光束等倾干涉的光学装置, 但它又不同于文献[9-11]和教科书中的平行膜多光束干涉方式. 我们推导了正三角形干涉装置的光程差的公式及其干涉斑纹的亮暗极值条件,解析推导并分析了其干涉斑纹的分布规律,并在结语中提出尚待解决的若干开放的问题.
1 正三角形光学腔双光束干涉光路图
如图1-图4所示是一种正三角形光学腔ΔABC, 边长为a,其中AB是全反射镜,AC、BC是两块相同的能够部分反射部分透射的平板光学玻璃, 但BC被截去一半,BO=BC/2=a/2,且腔内外空气媒质的折射率为n0≃1.00. 一般用于光学干涉实验的无膜平板玻璃,标称厚度大约5 mm左右. 当一束真空波长为λ的光线I以任意入射角i(入射光束被限制在30°左右),并在BO上任意点P入射,腔外得到反射线I′,腔内部分经各边顺次反射之后形成反射回路PP1→P1P2→P2P3,其中腔内反射线P2P3(即I″ )交OC于P3;当入射光束被限制在入射角i=30°左右很小范围,经两次折射与反射后的出射光I″(P2P3)不经过光学玻璃BO,直接射出并和反射光

图2 入射角i略大于30°的光路图
交于图1、图2中的D点, 或图3、图4中的无穷远处(或凸透镜的焦点).
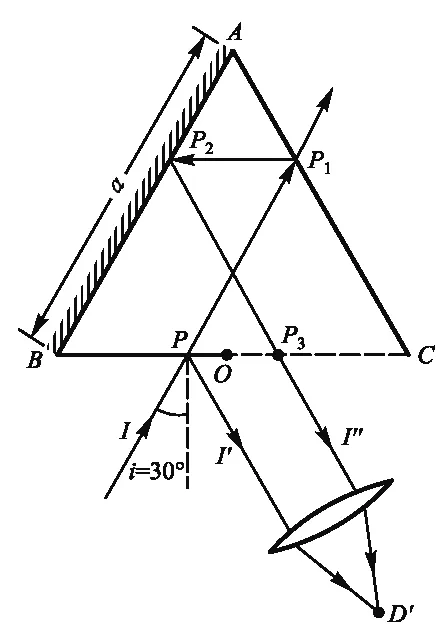
图3 左入射i=30°时的光路图
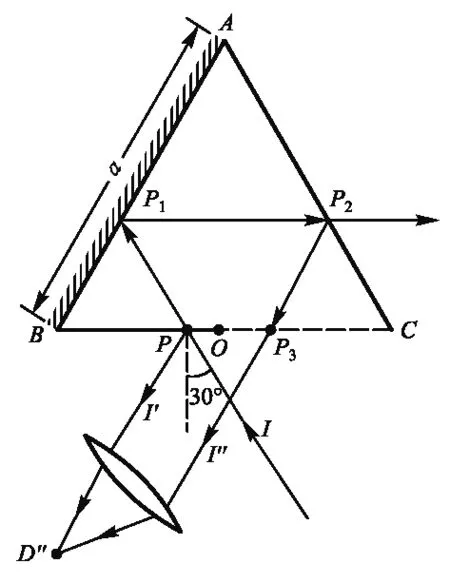
图4 右入射i=30°时的光路图
如图1—图4所示,首先可证:当入射角i略小于30°,此时反射光线I′与反射光线I″ (即P2P3) 的反向延长线交于AB上侧D点;当入射角i略大于30°,反射光光线I′与反射光线I″的延长线交于BC下侧D点;当入射角i=30°,反射光线I′与反射光线I″平行, 交于凸透镜焦点D′或D″点(分别从法线左右两侧入射时) .
这是因为ΔABC为等边三角形,∠A=∠B=∠C=60°,根据反射定律,P1处入射角为60°-i;P2处入射角为i, 且 ∠PP1C=30°+i;∠PP1P2=2(60°-i); ∠AP1P2=∠PP1C=30°+i;∠P1P2P3=2i. 如图1所示,当入射角i略小于30°,在ΔPP3D中, ∠DPP3=90°+i;∠DP3P=30°+i;最后推得∠PDP3=2(30°-i);此式表明,当入射角i略小于30°,则∠PDP3=2(30°-i)>0°,说明此时反射光线I″与反射光线I′的反向延长线交于AB上侧D点,如图1所示.
当入射角i略大于30°,此时若按图1计算,则得∠PDP3=2(30°-i)<0°,矛盾,故交点D不应在AB上方腔外,而应在BC下方的D点;如图2所示,在ΔPP3D中, ∠DPP3=90°-i,∠DP3P=150°-i,此时∠PDP3=2(i-30°)>0,可知反射光线I″与反射光线I′的延长线确实交于BC下侧的D点.
特别地,当入射角i=30°,并从法线左侧入射,则∠PDP3=2(30°-i)=0°,交点D趋于无穷远处,此时反射光线I″与反射光线I′平行,通过凸透镜相交并干涉于其焦平面上D'点,如图3所示. 而当入射角i=30°,并从法线右侧入射,∠PDP3=2(30°-i)=0°,交点D趋于无穷远处,此时反射光线I″与反射光线I′平行,通过凸透镜相交并干涉于其焦平面上D″点,如图4所示.
2 光程差公式与干涉条件
其次可证,无论反射光线I″与反射光线I′相交于D点,或无穷远处,其几何光程差都与入射点P的位置无关,亦即与BP=x无关,而仅依赖于入射角i及ΔABC的边长a,因而满足双光束等倾干涉条件. 以入射角i略大于30°的图2情形为例,我们推导交点D处的光程差ΔL及相位差δ的表达式,并讨论其干涉条纹的亮暗条件. 从P点开始计算光程差,反射光I′的表观光程为PD,透射光的表观光程为PP1+P1P2+P2P3+P3D+Δ0,光程差为
ΔL=PP1+P1P2+P2P3+P3D+Δ0-PD+λ/2
(1)
其中计入了反射半波损失,而来自于半透型平板光学玻璃BO内的光线穿过一定倾斜路径(设长为h) 所带来的附加光程,n为半透型平板光学玻Δ0=nh璃的折射率. 它给相位差δ带来一个常数附加δ0=2πnh/λ. 这只会给干涉斑点或条纹带来级序或位置的平移变化,不影响干涉场整体的相对分布规律.
根据光线反射定律与平面几何知识:∠PP1C=30°+i;∠PP1P2=2(60°-i);∠AP1P2=∠PP1C=30°+i;∠P1PC=90°-i;∠PP1C=30°+i;∠AP1P2=∠PP1C=30°+i;∠AP2P1=90°-i;∠BP2P3=∠AP2P1=90°-i;∠BP3P2=30°+i;∠DPP3=90°-i;∠DP3P= 150°-i;∠PDP3=2(i-30°), 在三角形ΔPP1C,ΔAP1P2,ΔBP2P3和ΔPP3D中分别运用正弦定律,并设BP=x,则PC=a-x,可分别求得:
(2)
(3)
(4)
P3D=PP3cosi/sin2(i-30°)
(5)
PD=PP3sin(30°+i)/sin2(i-30°)
(6)
PP3=(2a-x)cosi/sin(30°+i)-(x+a)
(7)
(8)
将上述式(2)—式(6)代入光程差ΔL式(1), 及相位差公式δ=2πΔL/λ,并做整理可得
(9)
(10)
特别地,当i=30°,即如图3、图4所示的情形,光程差ΔL与相位差δ分别为:
ΔL=3a/2+λ/2+Δ0;δ=3πa/λ+π+δ0
(11)
显然光程差ΔL、相位差δ仅和入射角有关,并随入射角i而变,而与BP=x无关,即与入射点P的位置无关.
综上所述,如图2所示,腔内外的两束反射光相交于D点,两束光的波长与频率相同,并具有仅依赖于入射角与边长的一定的光程差,满足双光束相干条件,应能观察到定域于D点的亮暗干涉斑纹;由于入射角相同,光程差就相同, 从而形成双光束等倾干涉现象. 对于级序为k的亮暗干涉斑点,当
ΔL=kλ,δ=2kπ,k∈N,亮斑.
(12)
ΔL=(k+1/2)λ,δ=2kπ,k∈N,暗斑.
(13)
其中N为正整数集合. 前述分析表明,当光束以i>30°入射时,而当光束以i<30°入射时,可凭肉眼逆着出射线,在图1中的D点处观察到干涉斑纹. 实际上图1、图2两种情形,也可使用凸透镜,在透镜后观察到定域于某点的干涉斑纹(D点经透镜的成像点). 而当i=30°,如图3所示(法线左侧入射),或如图4所示(法线右侧入射),此时运用凸透镜,两束平行光汇聚并干涉于其焦平面上D′或D″点. 综上所述,在图1—图4所示之4种情形,均可用凸透镜观察到干涉斑纹.
3 干涉场强分布函数与对比度分析
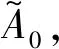
(14)
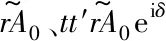
(15)
其中R=r2是半透型光学玻璃的能量反射系数. 可知D点处的干涉场的场强ID为
(16)
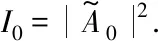
(17)
从AC膜处透射出去的光强IT为
(18)
根据式(16)中ID的表达式,当cosδ=±1时,其极大与极小值分别为:
IDmax=I0R(2-R)2;IDmax=I0R3
(19)
其中R∈[0,1],IDmax(R)的极大值为32I0/27(当R=2/3时), 最小值为零;IDmax(R)的最大值为I0,最小值为零. 点D处干涉斑纹的明暗对比度η为
(20)
上式表明,增大玻璃板的能量透射系数,或者减小平板玻璃表面的能量反射系数R,都能增加干涉斑纹的明暗对比度; 但是结合干涉场强表达式(16)、(19),可知能量反射系数R也不能太小,否则干涉场强ID直接趋于零了. 到底R多小为宜?显然R的选取应在增强明暗对比度η与增强条纹最大光强IDmax的两难选择之间达到某种平衡.
4 干涉斑纹的位置分布及其间隔
仍以入射角i>30°,i≈30° 的图2情形为例,如图2所示,取BC边为直角坐标系的X轴,点B为直角坐标系的原点,过原点B的Y轴垂直于BC边并朝下(为方便起见,选定左手系). 不妨设Δ0=0,设第k级暗斑Dk的入射角为ik, 则
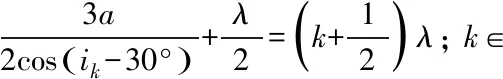
(21)
可求出
cos(ik-30°)=3a/2kλ
(22)
由此可知干涉级序k值受限于3a/2kλ≤1;k∈, 即kmin=[3a/2λ],中括弧意即圆整为整数. cos(ik-30°)=1即相应于ik=30°的平行光干涉的情形(D点趋向于无穷远处,用凸透镜可观察干涉现象),此时具有最低干涉级序kmin. 注意为使反射光线P2P3(I″)能在OC之间无障碍射出,i,x须满足条件:
a/2≤BP3=x+PP3≤a
(23)
可得P点位置x的极大值
(24)
及其允许范围0≤x≤xmax≤a/2, 由此可得其实验观察允许的入射角范围为
16.10°≤ik≤43.90°
(25)
具体而言,图2情形(ik≥30.00°)的实像干涉情形的允许入射角范围为
30°≤ik≤43.90°
(25)
而图1所示(ik<30.00°)的虚像干涉情形的允许入射角范围为
16.10°≤ik<30.00°
(26)
由式(22)又可求出

(27)
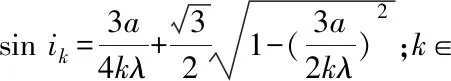
(28)
则干涉场的暗斑Dk的坐标(Xk,Yk)为
Xk(x,i)=x+PDsinik=
(29)
Yk(x,ik)=PDcosik=
(30)
从式(29,30)易知Dk的含参数的轨迹方程为
Xk(x,ik)=x+Yk(x,ik)tanik
(31)
由于相位差与P点位置即x无关,再由式(27-29)可知,在ik不变时,入射点P的平移不会改变干涉级序k值,但第k级暗斑的位置将在一条直线段上连续移动,形成暗纹,如图5所示.

图5 第k级暗斑随入射点x的移动而形成暗纹(干涉级序k=119100;a=0.05 cm;ik=36.65°)
另一方面,在保持入射点P不动,即x不变的条件下,改变入射角i,使之满足不同级序k的暗斑条件i=ik,k=119100+i,i=0,1,2,…7;取定腔体边长数a=5 cm;入射点x=a/4;入射波长λ=632.8 nm,用软件绘制出暗斑分布图Xk(ik)-Yk(ik),如图6所示. 尤须指出,从式(31)可知, 因为tanik随不同级序k值而变,Xk(ik)与Yk(ik)之间并不是线性关系,斑点的分布图形严格而言并不是直线,但由于图6中所取的k值范围使得式(31)中tanik近似不变,因此不同级序干涉斑点分布的局部轨迹近似于一段直线.
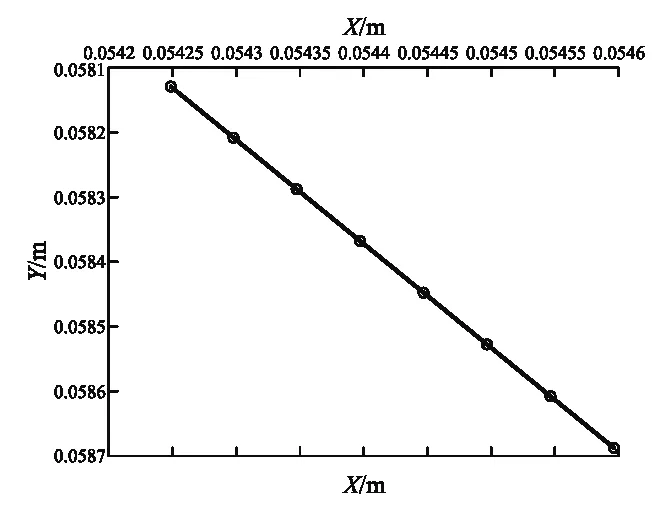
图6 固定入射点x时,不同级序斑点的分布图(参数a=5 cm, λ=632.8 nm;x=a/4;斑点级序:k=119100+i; i=0,1,2,…,7;入射角近35)
下面再计算相邻第k级、k+1级干涉暗斑的间隔dk=DkDk+1,即Dk(Xk(x,ik),Yk(x,ik))与Dk+1(Xk+1(x,ik+1),Yk+1(x,ik+1))的间距dk为
dk(x,a,λ;k)=DkDk+1=
(32)
将式(29,30)分别代入tanik=sinik/cosik及式(32),即得距离dk的严格解析表达式;而式(32)仅在tanik≐tanik+1的情况下近似成立.
前述间距公式表明:相邻干涉斑点的间隔与级序k值或入射角(ik,ik+1)有关,并与x,a,λ有关. 如欲使干涉斑纹肉眼可辨,须使相邻斑纹的间隔dk(x,a,λ;k)≥1 mm; 这就是腔体尺寸a与波长λ、级序k所须满足的条件. 如果相邻斑纹的间隔很小,则须用读数显微镜进行观测. 为使读者有一个简单而直观的印象,不妨取λ=632.8 nm, 在不用凸透镜观察的情况下,我们分别在三种情形给出如下参考数据:1)a=5 cm(宏观情形),入射点P在BO的中点:x=a/4,k=119100,ik=35.65°,斑纹位置在Dk(5.46 cm,5.87 cm);相邻条纹间隔dk=8.29 cm;2)a=7.5 μm (微观情形),x=a/8,k=18,ik=39.01°,斑纹位置在Dk(7.1 μm,7.7 μm);相邻条纹间隔dk=9.5 μm;3) 而对于腔体边长a=1 mm的中间尺度情形x=a/4,k=2371,ik=31.27°,斑纹位置在Dk(3.0 mm,7.7 mm);相邻条纹间dk=9.1 mm, 显然肉眼可辨. 另一方面,理论分析与计算表明,在保持a,λ及入射点x不变的前提下,随着级序k值增加,入射角ik也增加,斑纹坐标值减小,斑纹位置离装置(入射点P)越近,斑纹处相邻条纹间隔也越小;反之,随着k值和入射角ik(从最大允许入射角43.9)逐渐减小,斑纹位置离装置(入射点P)越远,斑纹处相邻条纹间隔dk也越大,直至ik减小至30°,斑纹位置趋于无穷远处,此时干涉级序k值有最小值,kmin=[3a/2λ],一般用凸透镜观察平行光的干涉现象,如图3、图4所示.
5 可能的应用前景
这种干涉结构不仅在光学科研与教学方面具有理论研究的意义,而且具备技术应用的现实可能性. 在以i=30°入射时,根据其光程差公式与干涉斑点亮暗条件(11-13),如能让平板玻璃AC沿着BC方向(X轴方向)平移,或者让BO光学板沿着垂线AO方向(Y轴方向)平移,就能在各自平移过程中保持ABC为正三角形. 如此则通过D(D′、D″)处干涉斑点的吞吐数目ΔN,配置以机械传动装置,即可实现对边长AB方向和高线AO方向位移的光学传感,精度可达1 μm;如果在记录亮(暗)斑吞(吐)的数目ΔN的同时又记录其所花时间Δt,则可同时实现对二维微位移速度的传感测量. 而且这种等边三角干涉装置结构对称,操作简便. 当然这种干涉结构对其位移传感量程的限制,在于不能让光线超出各自的合理范围或者逸出透镜的接收孔径.
另一方面,对于给定尺寸的正三角结构光学干涉腔,按照图3、图4的i=30°单色平行光入射方式实现双光束干涉,也可以根据干涉明暗条件(11-13),很方便地测定入射光波长,或者反过来测定正三角形光学腔的结构参数——边长a或高线长. 对于非30°入射情形的可能应用,尚有待于作者的继续研究与读者的发现.
6 结语
研究表明,本文给出的正三角形干涉结构,当光线在i~30°附近入射的情况下,确实能够发生双光束干涉现象. 当i=30°时,干涉场定域于无穷远,可以运用凸透镜观测;当i≠30°时干涉场定域于有限远处,也可在凸透镜后侧观察到干涉斑纹. 本文推导了正三角形双光束干涉结构的光程差与相位差、及干涉场强与对比度的公式,分析讨论了干涉斑纹的极大与极小条件及其观察方法,定量地推导与分析了干涉斑纹的分布规律,特别是相邻条纹间隔公式,并讨论了其可能的应用前景.
当然,由于时间与经费的限制,我们目前的研究还仅限于入射光线在正三角腔的横截面(即纸面)情形的初步理论探索. 后续的工作将专注于实验对理论的检验工作,以及随之而来的一个自然产生的问题:当入射角ik~30°,且在保持ik不变的情况下,入射光线绕法线旋进若干角度,干涉斑纹又将如何变形?这个开放的问题,留待感兴趣的同仁赐教.
