基于改进模态推覆法的导管架平台弹塑性抗震性能

刘红兵，孙丽萍，艾尚茂，闫发锁，陈国明

(1.哈尔滨工程大学 船舶工程学院，哈尔滨 150001；2.中国石油大学(华东) 海洋油气装备与安全技术研究中心，山东 青岛 266580)

海底地震作为一种突发性海洋环境灾害，具有持续时间短、震级大、破坏性强等特点[1]，如1969年渤海湾7.4级地震、2004年印度洋9.4级地震以及2011年日本Tohok-Oki 9.0级地震等，严重威胁海洋导管架平台的服役安全[2].现阶段关于导管架平台的抗震设防尚缺乏统一的专业规范，主要参考美国石油学会(API)以及建筑结构工程等领域相关的设计规范.其中，API规范要求设计地震下，海洋导管架平台结构需满足强度要求，即结构和基础均无破坏；罕遇地震下平台需满足韧性要求，即允许结构和基础有一些损伤，但结构不能倒塌[3].而建筑工程规范则要求结构满足“两阶段，三水准”原则，其中“两阶段”分别指弹性抗震和弹塑性抗震阶段，“三水准”则指“小震不坏、中震可修、大震不倒”的定性准则[4].这些规范准则对于海洋导管架平台的线弹性抗震设防具有较好的设计指导作用，但对于强震下平台结构的非线性弹塑性抗震性能以及平台结构地震失效机制等问题尚缺乏深入研究.而对于海洋导管架平台，通常结构冗余度较大，传统的线弹性抗震评估方法无法准确评估这种大冗余度结构的弹塑性抗震性能，因而准确地评估强震下平台结构的弹塑性地震响应，对于保证海洋导管架平台的抗震设计及其安全运行具有重要意义.

目前，海洋导管架平台的抗震设计分析方法主要有静力法、反应谱法、动力时程法、弹塑性推覆法等.静力分析法通常将地震作用等效为一种侧向惯性载荷作用，并采用地震系数修正地震过程中的动态效应，但由于平台结构和地震动之间耦合作用的复杂性，导致地震系数难以准确确定，从而容易产生较大的误差[5-6].反应谱法又称为等效静力分析法，通常通过振型分解将平台结构简化为单质点体系，然后采用单质点体系最大地震响应描述结构地震响应，该方法可以较好地获得简单结构的弹性地震响应，但却无法考虑强地震下平台结构的非线性弹塑性地震响应[7-8].动力时程法通过对平台结构输入时变地震动并进行动力积分，获得结构弹塑性地震响应，该方法可较好地反映结构动态地震响应，但由于地震动的随机性和差异性，即使具有相同控制参数的不同输入地震动时程，也可能导致结构地震响应相差巨大[9-10].弹塑性推覆法(能力谱法)通过将设计反应谱引入结构抗震性能评估，可较好地识别结构弹塑性抗震性能以及抗震薄弱环节和破坏机制，已在结构工程领域获得广泛认可，并被美国、日本、韩国等规范纳入，但该方法主要基于结构基本振型和形状向量保持不变的假设，忽略了高阶振型以及塑性抗震阶段结构振型向量发生变化的影响，从而在平台结构实际弹塑性抗震设计中具有一定的局限性[11-13].为此本文以渤海某导管架平台为研究对象，建立一种适于海洋导管架平台弹塑性抗震性能评估的改进模态推覆(IMPA)法，对比分析不同分析方法(能力谱、动力时程和改进模态推覆法)下，平台结构弹塑性抗震性能的差异性，探讨高阶振型和振型向量对平台结构弹塑性抗震性能的影响，识别平台结构抗震薄弱环节，相关结论和研究成果可为海洋石油导管架的平台抗震设计提供理论依据和工程参考.

1 模态推覆法(MPA)理论基础

海洋导管架平台服役环境恶劣，地震作用下除了受到海床震动对结构产生的惯性载荷外，还将受到地震引发海水对结构产生的附加载荷作用.由于海水附加质量产生的惯性载荷对平台结构的地震响应影响较小，故可将其忽略.根据非线性结构动力学原理可建立地震载荷作用下，海洋平台结构弹塑性抗震运动的微分方程为

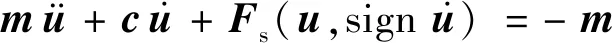
(1)

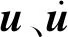
假设平台结构地震响应主要由结构前n阶振型控制，则根据振型分解的基本思想，对式(1)进行解耦即可得到平台结构运动的微分方程为

(2)

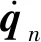
由式(2)可知，地震载荷作用下的平台结构恢复力函数依赖于各模态坐标之间的耦合作用，但由于此时的平台结构响应仍以n阶模态为主导，可忽略各模态坐标之间的耦合作用[14-15]，所以式(2)可采用类似于弹性体系的强迫解耦算法进行解耦.假定平台结构地震作用下n阶模态单自由度体系(SDOF)的位移响应为

(3)

式中：Dn为平台结构n阶模态单自由度体系位移响应向量；I为单位矩阵；qn为n阶振型模态位移.将式(3)代入式(2)，整理可得平台结构单自由度体系n阶振型运动方程为

(4)

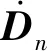
(5)

式中：Vb,n为平台结构n阶模态剪力.平台结构等效单自由度体系屈服剪力Vb,ny和屈服位移Dny为

(6)

式中：Fs,ny为n阶模态屈服剪力所对应的恢复力；ur,ny为n阶模态结构顶点屈服位移；φr,n为n阶模态顶点振型值.根据式(6)即可获得平台结构n阶模态单自由度体系的等效能力曲线，如图1所示.

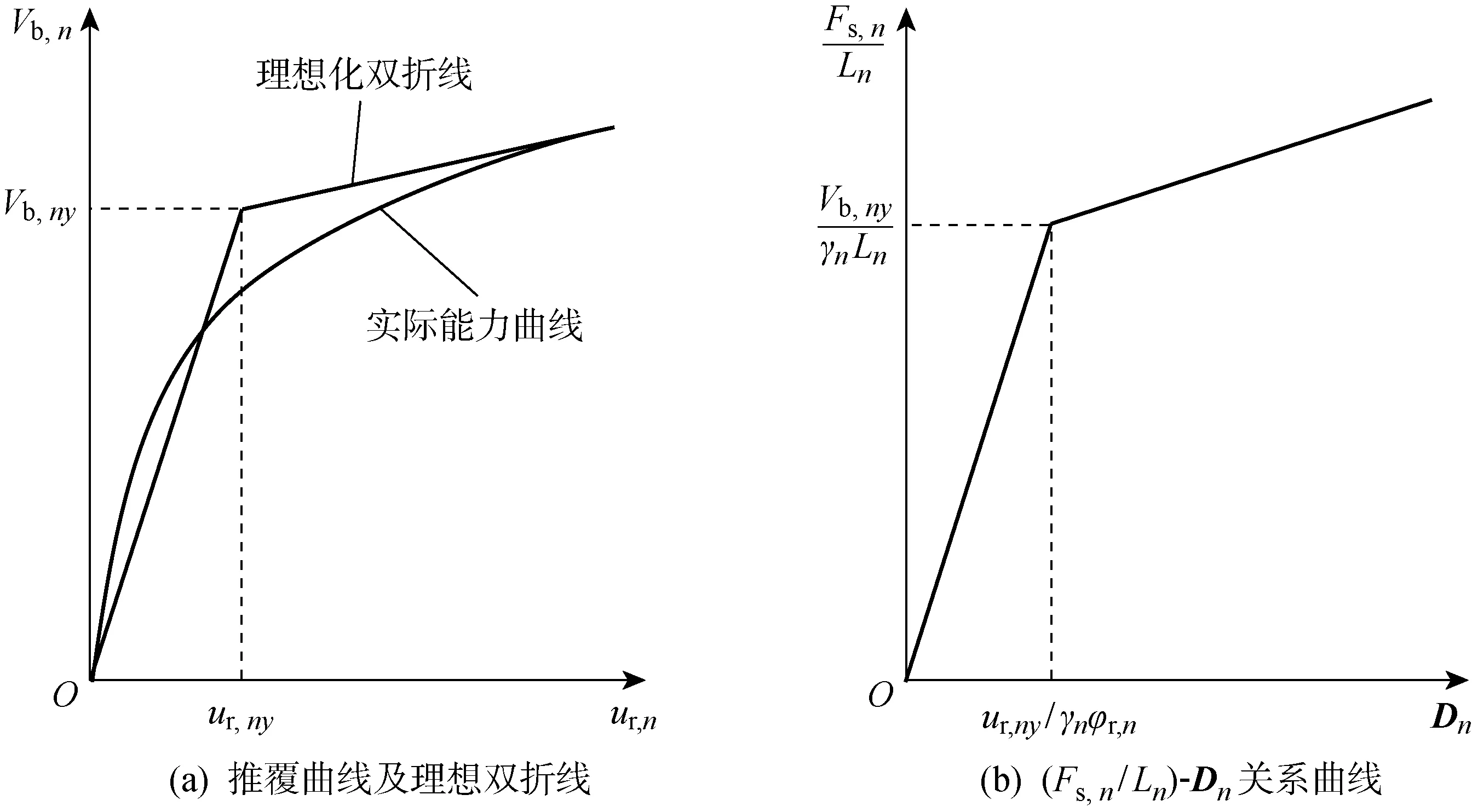
图1 平台结构等效单自由度体系能力曲线Fig.1 Capacity curve of equivalent single-degree-of-freedom system of platform

根据平台结构n阶模态等效单自由度体系，即可求得n阶模态的有效周期为

(7)

进一步将各阶振型下平台结构的地震响应进行叠加组合，即可得到地震载荷作用下的平台结构响应，表达式为

(8)

2 改进模态推覆法

2.1 改进模态推覆法的基本原理及分析步骤

模态推覆法通过振型组合的方式对平台结构进行抗震性能评估，该方法可以考虑高阶振型对平台结构抗震性能的影响，但是在各阶振型分析过程中采用统一的位移形状向量，忽略了平台结构由弹性抗震阶段转变为弹塑性抗震阶段形状向量发生变化的影响，从而导致模态推覆法的评估结果与平台结构实际抗震性能不相符.对于导管架平台结构，在弹性抗震阶段时，结构形状向量保持不变，但当平台结构发生屈服进入弹塑性抗震阶段时，其结构刚度和位移形状向量均发生改变，理想的计算方法是将上一步地震载荷作用下的结构位移向量作为下一步地震载荷作用下的形状向量，这样形成的弹塑性抗震分析方法与平台结构地震载荷作用下的实际受力情况最吻合，但同时会导致计算非常复杂且计算量巨大.根据MPA法获得的平台结构抗震能力曲线可知(见图1)，平台结构进入塑性抗震阶段后，抗震能力曲线的切线刚度虽然一直在变化，但其变化量却较小，故可近似采用塑性阶段的等效折线斜率代替平台结构的塑性刚度.因而IMPA法的基本思想为在弹性抗震阶段，采用平台结构弹性自振形状向量进行抗震分析；在弹塑性抗震阶段，则采用结构塑性阶段的等效折线斜率所对应的平台结构位移向量进行抗震分析.

IMPA法的具体流程如图2所示，主要分析步骤如下：① 建立平台结构的有限元模型，计算平台结构各阶的自振频率ωn和振型φn；② 计算平台结构各阶振型质量参与系数，确定有效参振振型；③ 以平台结构的n阶振型φn作为初始形状向量，对平台结构施加侧向载荷Fn1=mφn，开展推覆分析，获得平台结构n阶振型的推覆能力曲线；④ 根据图1，将平台结构的n阶振型推覆能力曲线简化为等效双折线模型(推覆能力曲线和双折线与x轴围成的面积相等)，并进一步建立平台结构线弹性n阶振型等效单自由度体系能力曲线((Fs,n/Ln)-Dn关系曲线)；⑤ 若平台结构发生屈服，进入塑性抗震阶段，可在平台结构推覆能力曲线上选择一点，使得该点切线的斜率和简化后的等效折线斜率相等，然后将该点处所对应的位移向量作为平台结构塑性抗震阶段的形状向量φn1，对平台结构施加侧向载荷Fn2=mφn1，进行第2次推覆分析，获得平台结构塑性抗震阶段推覆能力曲线；⑥ 组合平台结构弹性和塑性抗震阶段推覆能力曲线，并建立平台结构弹塑性n阶振型等效单自由度体系能力曲线；⑦ 组合各阶振型下平台结构的地震响应，计算平台结构的总地震响应，并评估平台结构的抗震性能.

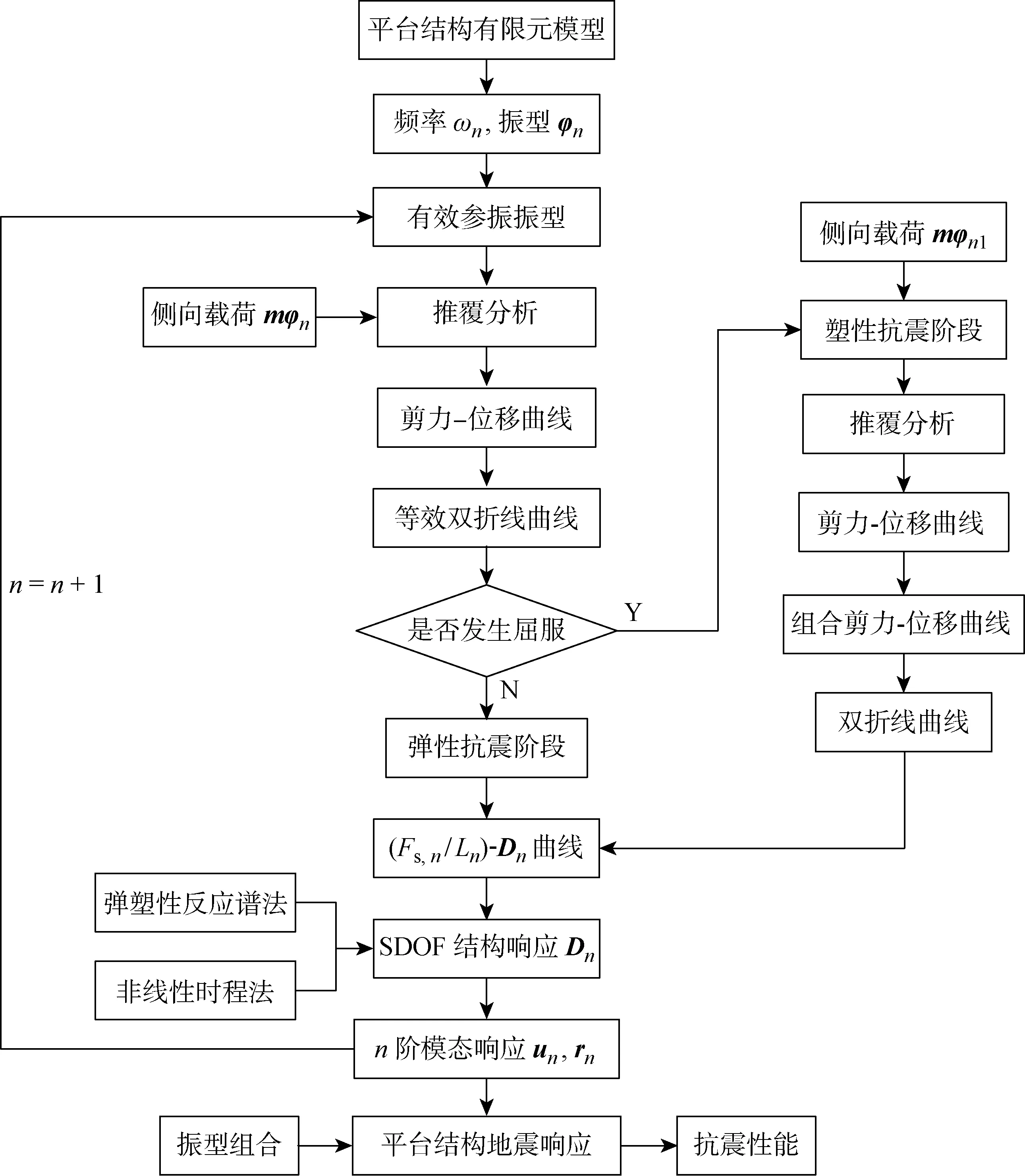
图2 IMPA法的基本流程图Fig.2 Basic flowchart of IMPA method

2.2 改进模态推覆法的有效振型

地震载荷作用下，海洋平台结构各阶振型对平台结构总体反应的贡献大小差异较大，如何选取合适的参振振型对于提高平台结构抗震性能评估的准确度和减小计算量具有重要的意义.目前，关于海洋导管架平台结构抗震设计过程中有效参振振型的选取没有具体规范，主要参考建筑结构抗震设计规范，即不考虑扭转时，若结构基本周期小于1.5 s，可取2～3个振型，若基本周期大于1.5 s或高宽比大于5时，振型数可适当增加；考虑扭转时，可取前9～15个振型[4]，然而海洋导管架平台结构抗震性能与陆地建筑结构的差异较大，参考陆地建筑规范选取有效参振振型可能会导致较大的误差.因而，本文采用振型质量参与系数法确定有效参振振型，即保证所有参振振型的参与质量不小于平台结构总质量的90%[16].

平台结构n阶振型广义质量为

(9)

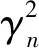
(10)

根据式(10)，定义平台结构n阶振型参与质量为平台结构n阶振型广义质量与n阶振型参与系数平方的积，具体表达式为

(11)

式中：me,n为平台结构n阶振型的参与质量.平台结构n阶振型质量参与系数an为

(12)

将式(12)按照x、y和θ方向分解，即可得到平台结构不同自由度下各阶振型质量参与系数，表达式为

(13)

式中：ME,nx和ME,ny分别为平台结构n阶振型参与质量在x方向和y方向上的分量；ME,nθ为n阶振型参与质量θ方向的转动惯量；Jn为平台结构n阶振型的转动惯量.

3 算例分析

3.1 平台结构有效参振振型

以文献[1]中渤海某导管架平台为研究对象进行分析.该平台为4桩腿导管架平台，主要由桩腿、导管架和上部组块等构成，其中平台底部标高为 -15.0 m，上部组块顶部标高为20.0 m.为充分了解该平台结构自振特性及其扭转效应，系统地分析了平台结构前20阶自振频率和模态振型特征，其中前6阶自振频率和模态振型如图3所示，其中f为频率.由图3可知，平台结构基本自振频率为1.84 Hz，1阶振型为平台沿y轴平动，2阶振型为平台沿x轴平动，3～5阶振型为平台绕3个坐标轴转动，6阶振型为平台沿z轴平动.

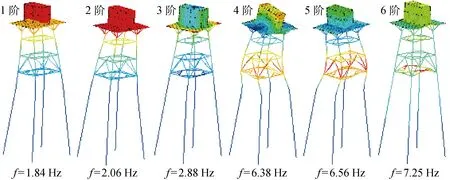
图3 平台结构前6阶模态振型图Fig.3 First 6 modal shapes of platform

根据式(13)分别计算平台结构6个自由度方向各阶振型质量参与系数，前10阶振型质量参与系数如表1所示，其中anz为n阶振型沿z方向的参与系数；ar,nx、ar,ny和ar,nz分别为n阶振型沿x、y、z轴旋转方向参与系数.由表1可知，平台结构x方向振型质量参与系数在前5阶累计达到98.89%，y方向振型质量参与系数在前4阶累计达到98.18%，z方向振型质量参与系数在前6阶累计达到95.78%，x、y、z轴旋转方向振型质量参与系数在前9阶累计均达到90%以上，因而采用改进模态推覆法对该平台进行弹塑性抗震性能评估时，可选取前9阶或9阶以上振型作为有效参与振型.同时由于平台结构地震响应主要集中于侧向x和y方向，其余方向地震响应相对较小，为减小计算量，仅考虑平台结构x和y两个方向的地震响应.进一步分析x和y方向振型的质量参与系数可发现，平台结构x方向振型质量参与系数主要集中于第2、5、9阶振型(累计振型质量参与系数为99.20%)，y方向振型质量参与系数主要集中于1、4、8阶振型(累计振型质量参与系数为99.22%)，因而可忽略其余振型对平台结构x和y方向地震响应的影响，即计算以上6阶振型对应方向的地震响应，然后通过振型组合方法获得平台结构整体的地震响应.

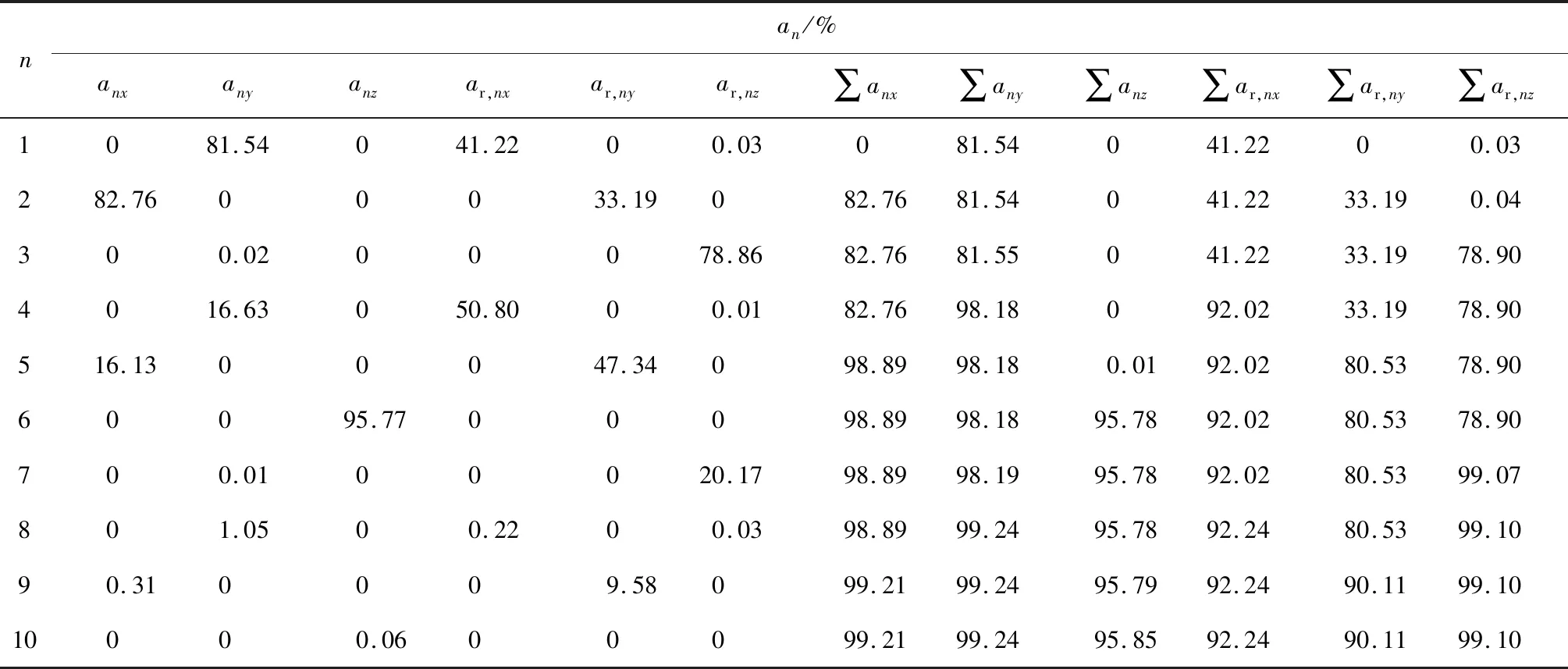
表1 平台结构各阶模态振型质量参与系数表Tab.1 Mode mass participation factors of platform

3.2 设防烈度8度地震响应

选取设防烈度为8度的地震(50年超越概率为10%，峰值加速度0.2g，g为重力加速度)，分别针对上述有效参振振型进行模态推覆分析，获得各阶模态振型下平台结构能力曲线和等效单自由度双折线.通过对平台结构各阶模态振型下顶点位移和基底剪力与等效屈服点(二折线交点)所对应的顶点位移和基底剪力之间的比较，判断不同模态振型下平台结构是否发生屈服，进入塑性抗震阶段，结果如表2所示.其中：ur为平台结构顶点位移；Vb为基底剪力.

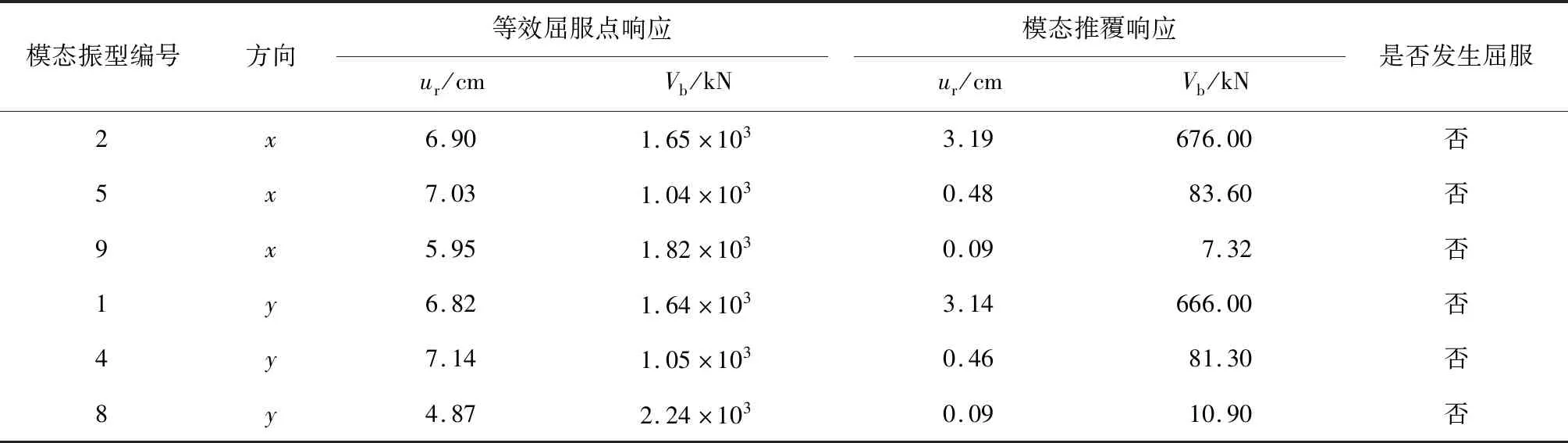
表2 设防烈度8度地震下平台结构各阶模态振型响应Tab.2 Modal responses of platform at 8 degree seismic fortification intensity

由表2可以看出，6个模态振型下的平台结构顶点位移和基底剪力均小于对应的等效屈服点顶点位移和基底应力响应，平台结构没有发生屈服，因而在后续模态推覆分析过程中可采用统一的形状向量.

上述各阶模态振型下的平台结构x和y方向位移响应图如图4所示，其中：h为平台结构垂向高度；u为侧向位移.由图4可看出，平台结构2阶模态振型下的x方向位移和1阶振型下的y方向位移显著大于其余各阶模态振型下的位移响应，平台结构地震响应以第1和2阶模态振型为主.2阶模态振型下平台结构x方向位移在导管架和上部组块区间段随着高度的增大而逐渐增大，而在导管架顶层和下甲板之间的斜撑区段，位移值随着高度的增大而减小，这主要是导管架和上部组块间质量和刚度矩阵的差异性所致；5阶模态振型下，x方向位移值为负，表明此时结构沿着x轴反方向振动；9阶模态振型下，x方向位移非常小，说明结构x方向的振动以第2和5阶模态振型为主，如图4(a)所示.与x方向位移类似，1阶模态振型下，平台结构y方向位移随着高度的增大而逐渐增大，且上部组块区间段的增大幅值小于导管架区间段；第4和8阶模态振型下，y方向的位移值较小，结构y方向振动以第1阶模态振型为主，如图4(b)所示.

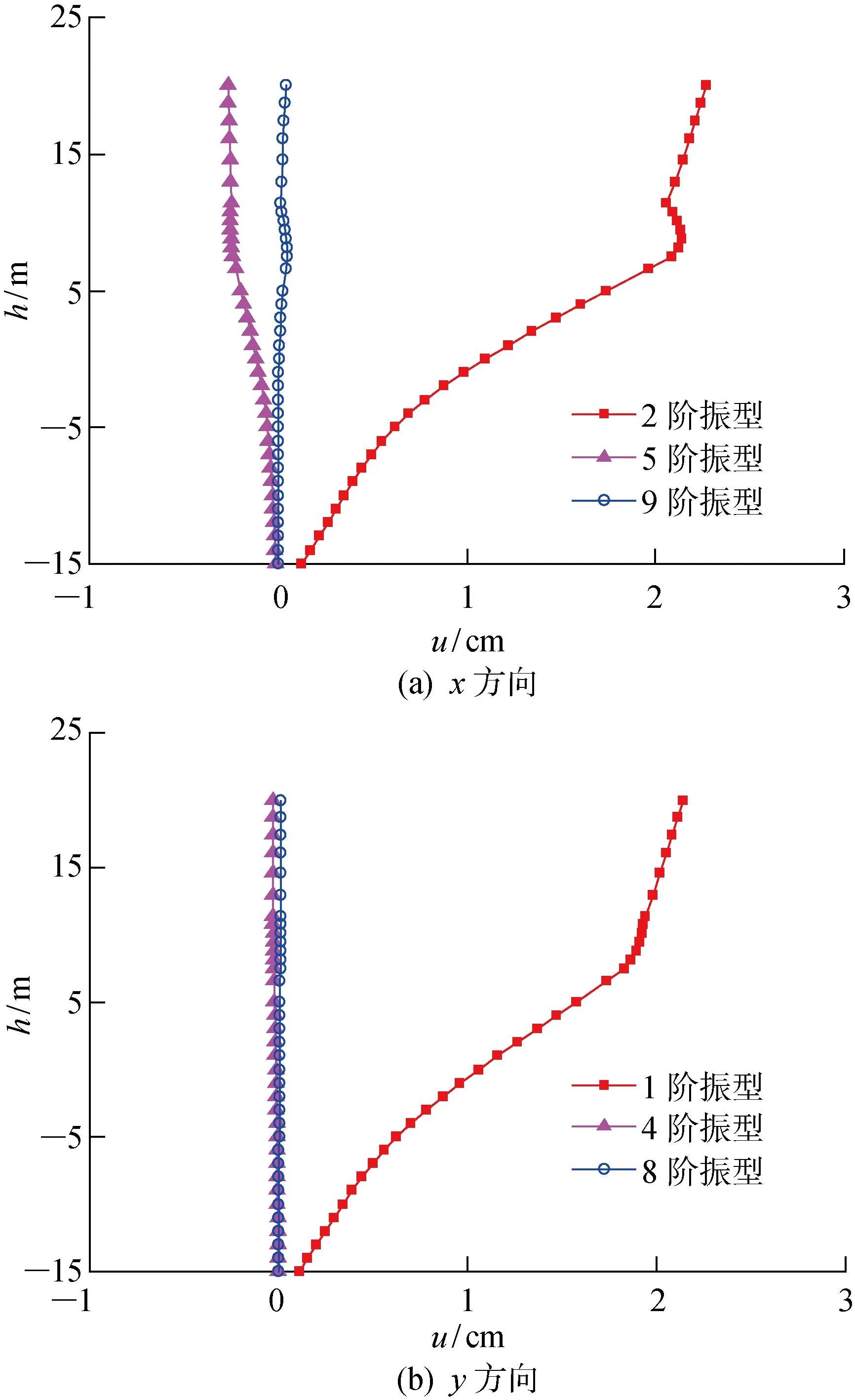
图4 各阶模态振型下平台结构x和y方向位移图Fig.4 Displacement curves in x and y directions of platform in different modal shapes

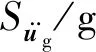
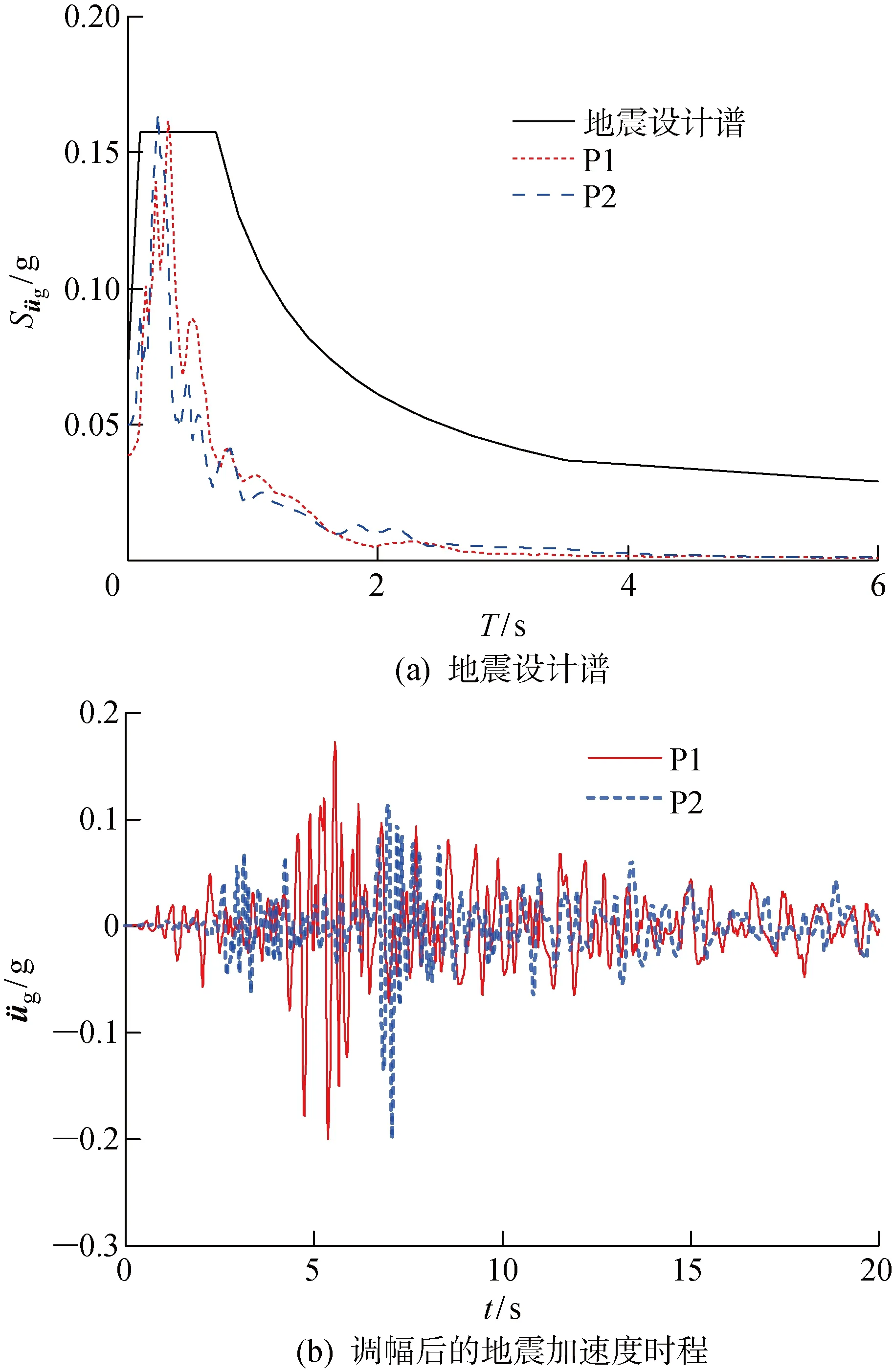
图5 P1和P2的地震加速度谱和时程Fig.5 Acceleration spectrums and time histories of P1 and P2 seismic

分别采用上述3种不同方法获得的平台结构地震位移和位移角(η)响应如图6所示.由图6可知，平台结构的最大位移均位于平台结构顶层，最大位移角均位于导管架顶端位置处.对比MPA法和能力谱法的位移响应可看出，在导管架下部区域，MPA法位移响应小于能力谱法；在导管架中间区段，MPA法和能力谱法的位移响应相差不大；在平台上部组块区域，MPA法的位移响应则大于能力谱法，其中MPA法的位移最大值为4.49 cm，能力谱法的位移最大值为4.21 cm，前者比后者增大了约6.65%，说明高阶振型对平台结构底部和上部组块结构的地震位移响应具有较大的影响，不可忽略.对比P1和P2地震时程分析法的位移响应可看出，不同地震时程作用下，平台结构的位移响应相差较大，其中P2地震位移响应在导管架区段和MPA法以及能力谱法的位移响应较为接近，在上部组块区段却小于MPA法和能力谱法的位移响应，而P1地震位移响应则远大于P2、MPA法以及能力谱法的位移响应.P1地震最大位移响应为6.27 cm，P2地震最大位移响应为3.97 cm，P1最大位移比P2最大位移约增大了58.12%，表明具有相同峰值加速度的不同输入地震时程，平台结构的地震位移响应表现出较大的离散性和差异性，如图6(a)所示.

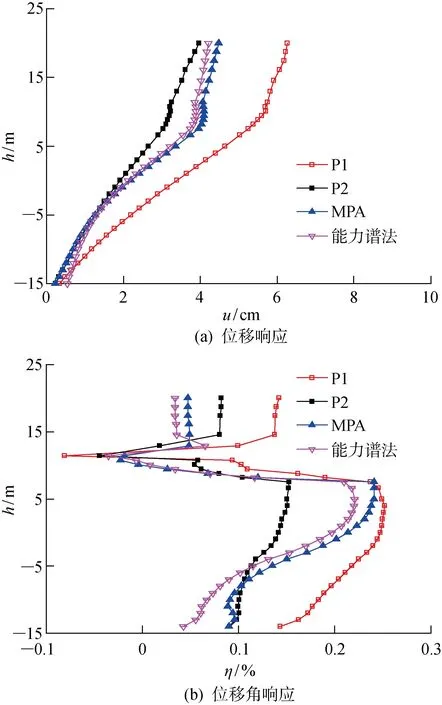
图6 设防8度地震下的平台结构地震响应Fig.6 Seismic responses of platform at 8 degree seismic fortification intensity

对比3种方法下的平台结构位移角响应可看出，平台结构的最大位移角均位于导管架顶端位置处，说明该位置处为平台结构的抗震薄弱环节，进行弹塑性抗震设计时需重点关注；MPA法和能力谱法下，平台结构的位移角整体形状类似，且MPA法的位移角整体略大于能力谱法的位移角，其中MPA法最大位移角为0.24%，能力谱法最大位移角为0.22%，MPA法最大位移角约增大了9.31%，进一步表明高阶振型对平台结构抗震性能的影响；P1和P2地震时程作用下，平台结构位移角随着高度的变化表现出更为复杂的变化趋势，其中P1地震位移角响应整体上大于MPA法和能力谱法位移角响应，P2地震位移角响应在导管架下部区域略大于MPA法和能力谱法响应，在导管架中部区域小于MPA法和能力谱法响应，在上部组块区域则又大于MPA法和能力谱法响应，如图6(b)所示.

3.3 罕遇烈度8度地震响应

由3.2分析可知，设防烈度8度地震作用下，平台结构没有发生屈服，处于弹性抗震阶段，为进一步研究平台结构弹塑性抗震性能，选取罕遇烈度8度的地震(50年超越概率为2%～3%，峰值加速度为0.4g，水平地震最大影响系数为1.2)进行抗震性能分析.根据前文所述的平台结构地震载荷作用下有效参振振型，分别开展模态推覆分析，获得各阶有效参振振型下平台结构能力曲线和等效单自由度双折线，并通过与等效屈服点的比较判断平台结构各阶振型下是否发生屈服，进入塑性抗震阶段，结果如表3所示.

由表3可看出，x方向的第2阶模态振型和y方向的第1阶模态振型下平台结构发生屈服，进入塑性抗震阶段，其抗震形状向量发生改变，故需采用IMPA法进行弹塑性抗震性能分析.

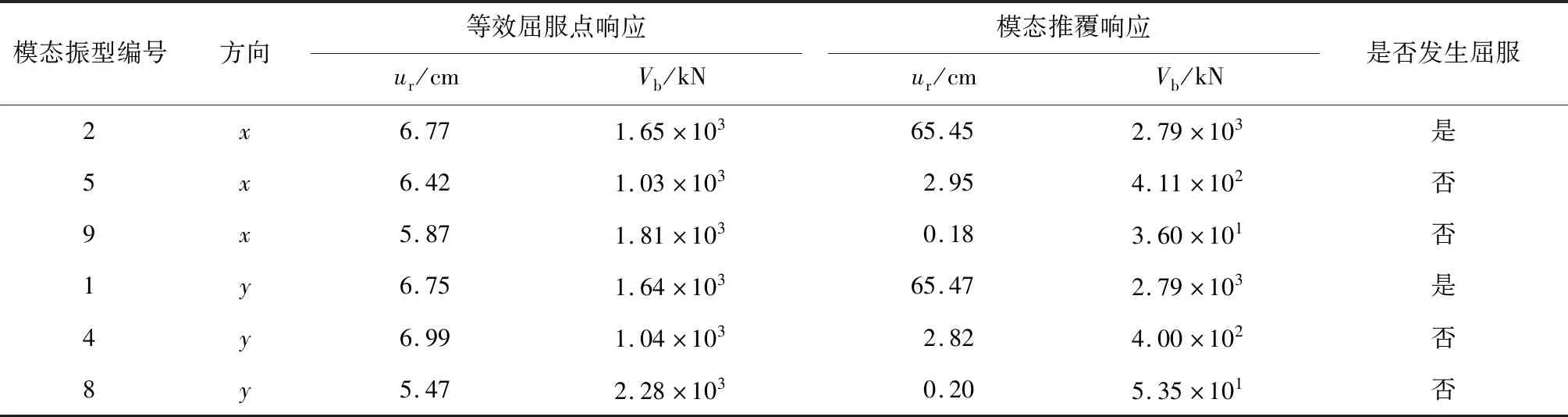
表3 罕遇烈度8度地震下平台结构各阶模态振型响应Tab.3 Modal responses of platform at 8 degree seismic rare intensity

分别采用IMPA法和MPA法，获得的平台结构在第1阶振型下y方向位移和第2阶模态振型下x方向位移的比较如图7所示.由图7可看出，两种方法下的平台结构x和y方向位移形状相似，其中在导管架部分，IMPA法和MPA法的位移响应相差不大.但从导管架顶部到上部组块区域，IMPA法的位移结果显著大于MPA法的位移结果.这主要是由于导管架的顶端位置处为抗震薄弱环节，结构在该位置处发生屈服进入塑性抗震阶段，使得导管架顶端上部组块位移显著增大所致.通过改变形状向量进行二次推覆分析的IMPA法，可较好地体现平台结构的弹塑性抗震性能特征，与平台结构的实际抗震状态较为吻合.

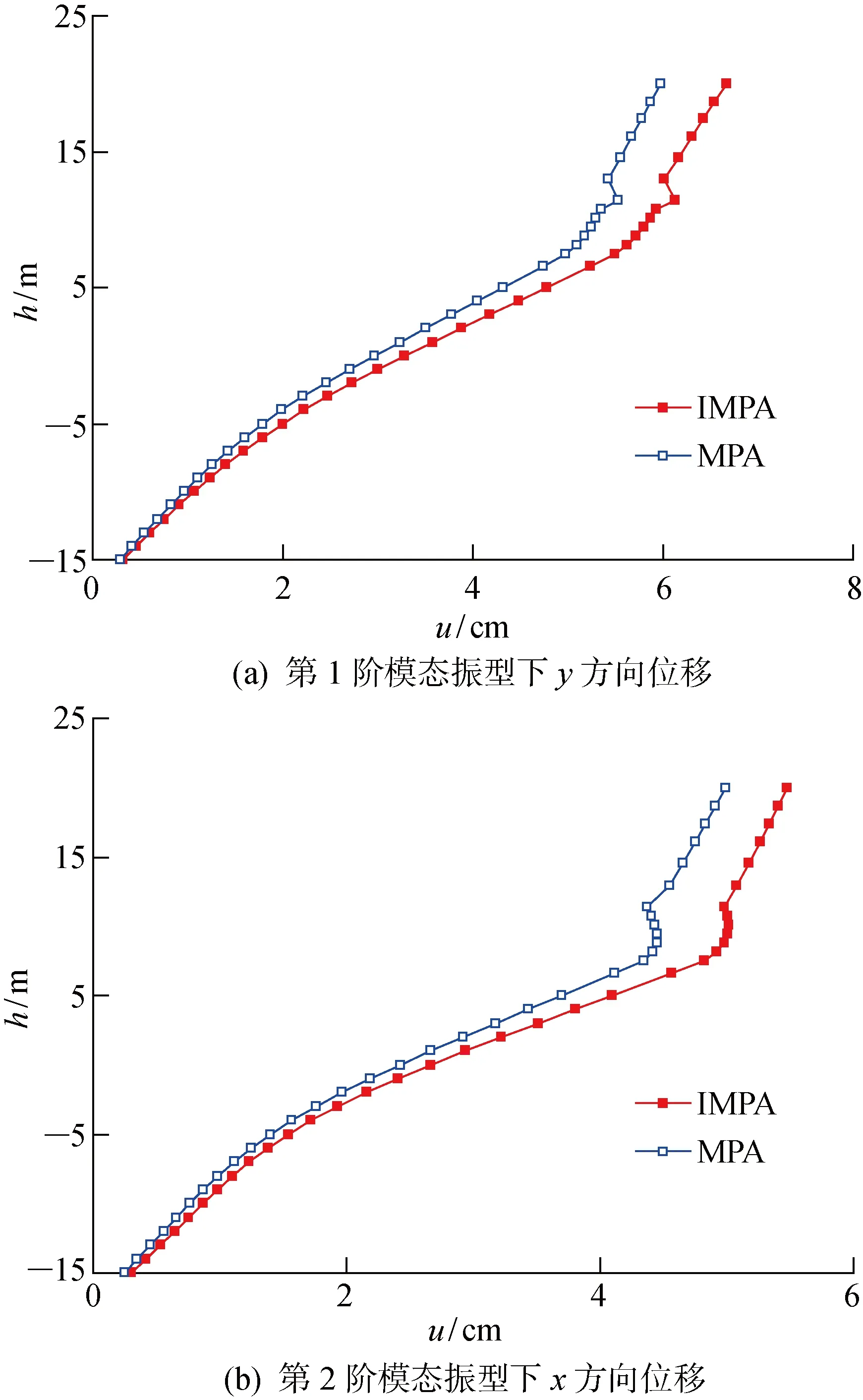
图7 IMPA法和MPA法分析结果比较图Fig.7 Analysis results of IMPA and MPA methods

采用SRSS振型组合法组合获得的平台结构整体地震响应，并分别同MPA法、能力谱法和时程分析法进行比较，其中时程分析法输入地震波仍采用调幅至峰值加速度为0.4g的P1和P2地震波，结果如图8所示.由图8(a)可看出，4种方法下平台结构地震位移响应随高度变化趋势基本类似，位移最大值均发生在平台顶点处；对比能力谱、MPA法和IMPA法平台结构位移可知，在导管架部分三者位移响应基本相等，但在上部组块区域，3种方法的位移响应表现出明显的差异，其中IMPA法位移响应最大、MPA法次之，能力谱法位移响应最小，这主要是由于随着高度增大，高阶振型影响逐渐增大以及平台结构塑性振动特性变化越来越明显所致.P1和P2地震波时程分析法结果相差较大，其中P1地震波作用下平台结构的位移响应均大于能力谱、MPA法和IMPA法位移响应，而P2地震波作用下平台结构位移却均小于其余3种方法的位移响应，进一步体现了不同的输入地震动特性对于平台结构抗震性能评估产生的巨大影响.对比4种方法平台结构的最大位移可知，IMPA法平台结构顶点的最大位移值为0.121 m，比MPA法的最大位移增大了7.64%，比能力谱法的最大位移增大了11.42%，比P1地震时程法的最大位移减小了8.01%，比P2地震时程法的最大位移增大了51.01%，充分说明对于罕遇强震，在无法获取准确的强震加速度时程情况下，采用能力谱法和MPA法评估平台结构的弹塑性抗震性能均会产生较大误差，建议采用 IMPA 法.

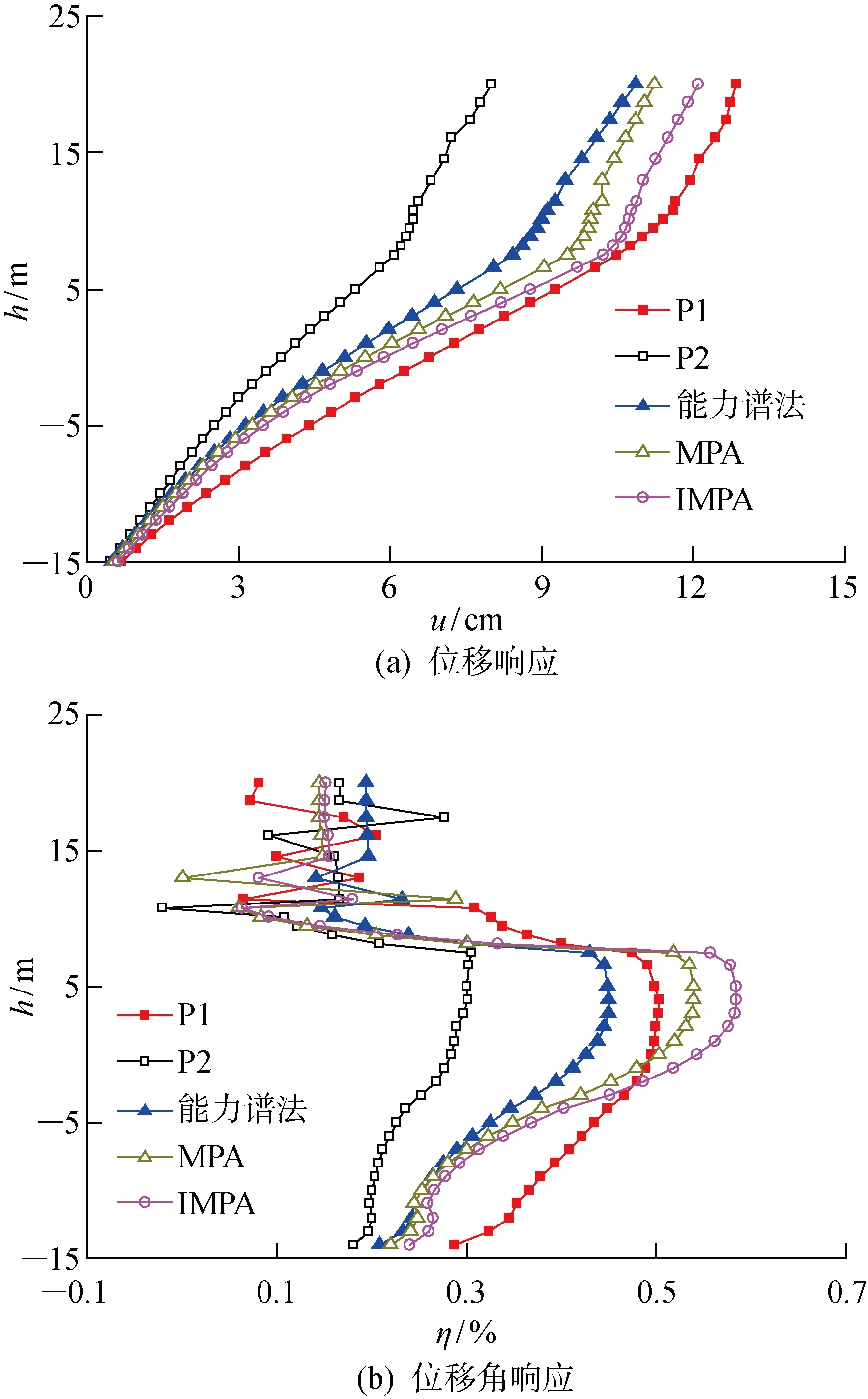
图8 罕遇8度地震下平台结构的地震响应Fig.8 Seismic responses of platform at 8 degree seismic rare intensity

由图8(b)可知，罕遇烈度8度地震作用下，平台结构位移角表现出更为复杂的变化特征，在导管架下部区域，P1地震时程法位移角最大，P2地震时程法位移角最小，IMPA法、MPA法和能力谱法基本相同，在导管架上部区域则变为IMPA法位移角最大，MPA法、P1地震时程法、能力谱法和P2地震时程法依次次之，在平台上部组块区域，位移角表现出明显的波动性，这主要是由于进入塑性抗震阶段后，平台结构的振动特性变得更为复杂所致.与设防烈度8度地震类似，平台结构地震最大位移角也均位于导管架顶端位置处，其中IMPA法最大位移角值为0.59%，MPA法为0.54%，能力谱法为0.45%，P1地震时程法为0.50%，P2地震时程法0.30%，均小于1%，但此时平台结构已经发生屈服进入塑性抗震阶段，与建筑结构工程中1%判据具有一定的差别，这主要是由于平台结构冗余度大，具有更高的侧向位移刚度，所以其侧向位移角相对较小.

4 结论

(1) 高阶模态振型对于平台结构弹塑性抗震性能影响较大，地震载荷作用下，平台结构x方向振型质量参与系数主要集中于第2、5、9阶振型，累计振型质量参与系数达99.20%，y方向振型质量参与系数主要集中于第1、4、8阶振型，累计振型质量参与系数达99.22%，因而为保证平台结构弹塑性抗震性能精度，需考虑平台结构前9阶或9阶以上的模态振型影响.

(2) 设防烈度8度地震下，平台结构处于弹性抗震阶段，最大位移和最大位移角分别位于平台结构顶点和导管架顶部，表明导管架顶部为平台结构抗震薄弱环节，需重点关注；不同分析方法下平台结构的最大地震响应相差较大，MPA法最大位移和最大位移角分别为4.49 cm和0.24%，比能力谱法最大位移和最大位移角分别增大了6.65%和9.31%，表明高阶振型对平台结构弹性抗震性能的影响.

(3) 罕遇烈度8度地震下，平台结构发生屈服，进入塑性抗震阶段，结构最大位移和位移角仍分别位于平台顶点和导管架顶部，其中IMPA法平台顶点最大位移为12 cm，比MPA法和能力谱法分别增大了7.64%和11.42%，IMPA法导管架顶部最大位移角为0.59%，比MPA法和能力谱法分别增大了9.26%和31.11%，进一步表明高阶振型和位移形状向量对平台结构塑性抗震性能的巨大影响.

(4) 具有相同峰值加速度的不同地震时程下平台结构地震响应表现出明显的离散性和差异性，当地震峰值加速度为0.2g时，P1和P2地震时程作用下平台结构顶点最大位移相差约58.12%；当地震峰值加速度为0.4g时，两者相差约60.47%.因而在无法准确获取地震时程情况下，时程分析法、能力谱法和MPA法均会产生较大误差，建议采用IMPA法评估平台结构弹塑性抗震性能.