一种双悬臂梁柔性销轴的微动疲劳研究
2021-04-07杨世平董梦瑜
杨世平,董梦瑜,李 飞
(湘潭大学 机械工程学院,湖南 湘潭 411105)
行星齿轮轴采用双悬臂梁结构,是重载行星传动实现均载的有效方法,此结构通过悬臂梁的弹性变形来实现均载,并可降低冲击载荷在系统中的传递,从而提升行星传动系统的可靠性[1].考虑到传动齿轮箱的结构限制和传动要求,销轴结构采用过盈配合装配方法.当柔性销轴承受由于轮齿啮合产生的周期性交变载荷时,过盈配合接触面会产生微小变形,导致微动疲劳的产生[2].微动疲劳会导致过盈配合表面磨损并萌生疲劳裂纹,缩短销轴结构的工作时间,使行星传动系统的寿命大大减小[3].因此,设计柔性销轴时需要考虑到微动疲劳的影响.
微动疲劳会严重影响到传动轴上配合结构的疲劳寿命,针对其微动疲劳特性,很多学者开展了相关研究.蒋春松[4]基于316L不锈钢进行了弯曲微动疲劳的试验研究,利用数值模拟分析了法向载荷、摩擦因数及循环载荷对接触面的应力应变作用.杨广雪等[5]在Abaqus软件中建立过盈配合接触模型,通过改变参数等手段分析套管长度、摩擦因数、套管厚度和过盈量对接触压力及摩擦剪切力的影响规律.曾飞等[6]利用ANSYS软件对铁道机车轮毂和轮座过盈连接接触表面在大载荷下的微动情况进行模拟分析,计算获得接触面内、外侧区域的某接触节点副的相对滑动规律和应力分布.Zhang等[7]基于疲劳试验机和高温试验机研究了温度、接触压力及滑移幅度对钛合金轴的微动疲劳性能的影响,并且通过对微动表面形貌特征的观察,研究了微动疲劳失效机理.宋川[8]在接触应力及弯曲载荷等参数下进行了轮轴缩比结构的弯曲微动疲劳试验,并通过仿真探究了轴的微动疲劳机理.刘大伟[9]在不同循环次数和弯曲载荷条件下,研究了30CrNiMo8合金钢的损伤规律,并通过观察断裂的试验品剖面,分析了疲劳裂纹的萌生及其扩展规律.张远彬等[10]基于临界平面法线性累计损伤模型建立了过盈连接微动疲劳的寿命估计模型,探究了微动磨损对其微动疲劳性能的作用.宫昱滨等[11]研究了过盈连接空心轴的微动磨损模型,经数值模拟得出结论,接触压应力、摩擦切应力和滑移幅值随着微动循环周次的增加而变大.
行星轮柔性销轴工作时受到频率较高和振幅较大的冲击载荷,柔性销轴的微动疲劳损伤对行星传动齿轮箱的寿命影响较大,尚未有学者针对此问题开展过具体研究.以2.5 MW齿轮增速箱内柔性销轴为研究对象,基于Lame公式计算销轴结构的应力应变、过盈量和最大弯曲载荷.基于理论计算将模拟仿真与疲劳试验相结合,分析弯曲载荷、过盈量、渗碳层深度这3个因素对微动疲劳损伤的影响,并观测受载后试件的表面形貌.基于SWT(Smith-Waston-Topper)模型对销轴结构进行疲劳寿命分析,研究柔性销轴的损伤机理并进行寿命预测,为柔性销轴抗微动疲劳损伤设计提供一定的理论参考.
1 过盈配合柔性销轴的理论计算
1.1 柔性销轴应力应变计算
据Lame公式[12],在销轴和套筒过盈配合的情况下,其应力应变公式为
(1)
(2)
式中:σr为径向力;σt为切向力;r1为销轴内径;r4为套筒外径;p1为内压力;p2为外压力;r为销轴结构的任意半径;u为径向位移;E为弹性模量;ν为泊松比.
过盈配合销轴结构剖面图如图1所示.其中:df为结合直径;da为套筒外径;lf为过盈结合长度.
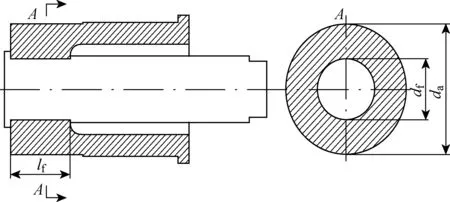
图1 过盈配合销轴结构剖面图Fig.1 Profile of interference fit pin structure
销轴结构受压示意图如图2所示.其中:r2为销轴外径;r3为套筒内径.柔性销轴过盈装配时,销轴与套筒相互作用,径向压力p1(内压力)作用于套筒的内表面,径向压力p2(外压力)作用于销轴的外表面[13].
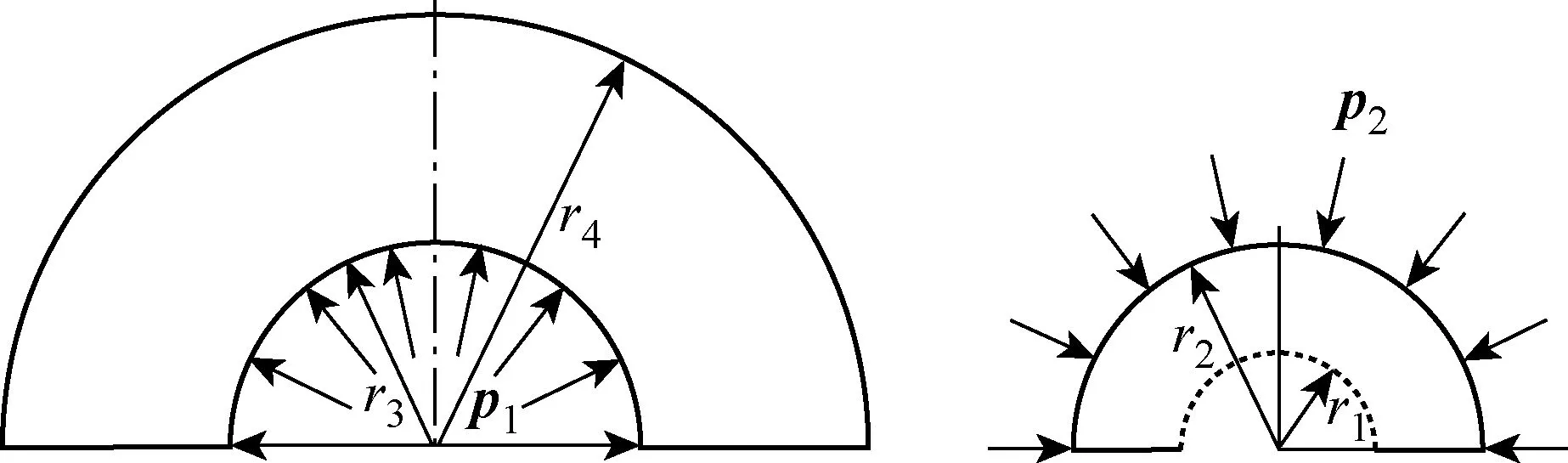
图2 柔性销轴受压示意图Fig.2 Schematic diagram of flexible pin under pressure
过盈配合表面的径向压力p1、p2可表示为
(3)
式中:Ea为套筒的弹性模量;Ei为销轴的弹性模量;δ为过盈量;Ca和Ci分别为套筒和销轴的刚性系数,可表示为
(4)
(5)
式中:νa为套筒泊松比;νi为销轴泊松比;rf为过盈配合半径;销轴内径r1=0.
过盈配合时,销轴承受压力p2时的应力、应变公式为
(6)
(7)
同理可知,过盈配合时,套筒承受p1时的应力、应变公式为
(8)
(9)
1.2 过盈量计算
1.2.1最小过盈量的计算 过盈配合表面最小结合压力pf_min为
pf_min=F′/(πdflfμ)
(10)
式中:μ为摩擦因数;F′为传递力.其计算公式如下:
(11)
Fx为过盈配合构件所受轴向力;M为传递扭矩.
在过盈配合时,套筒和销轴的最小有效过盈量δe_min为
(12)
计算满足结构要求的最小过盈量δmin为
δmin=δe_min+δs+δT+δv+δp
(13)
式中:δs为接触面粗糙度值对最小过盈量的修正量;δT为温度改变对最小过盈量的修正量;δv为旋转离心力对最小过盈量影响的修正量;δp为补偿重复压装时过盈量减小的修正量[14].
1.2.2最大有效过盈量的计算 套筒的最大结合压力为
pfa_max=aσsa
(14)
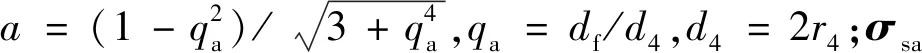
pfi_max=cσsi
(15)
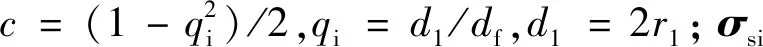
据以上,取pfa_max与pfi_max之中较低的结合压力作为柔性销轴的最大结合力pf_max.
在弹性范围内,过盈配合表面的最大有效过盈量δe_max可表示为
(16)
1.3 最大弯曲载荷计算
齿轮箱传动系统内各传动构件所承受的作用力等于反作用力.齿轮受载示意图如图3所示.径向应力Fr1与Fr2大小相等,方向相反,可平衡;柔性销轴所受切向力Ft1=Ft2,构件承受弯曲载荷的最大值为
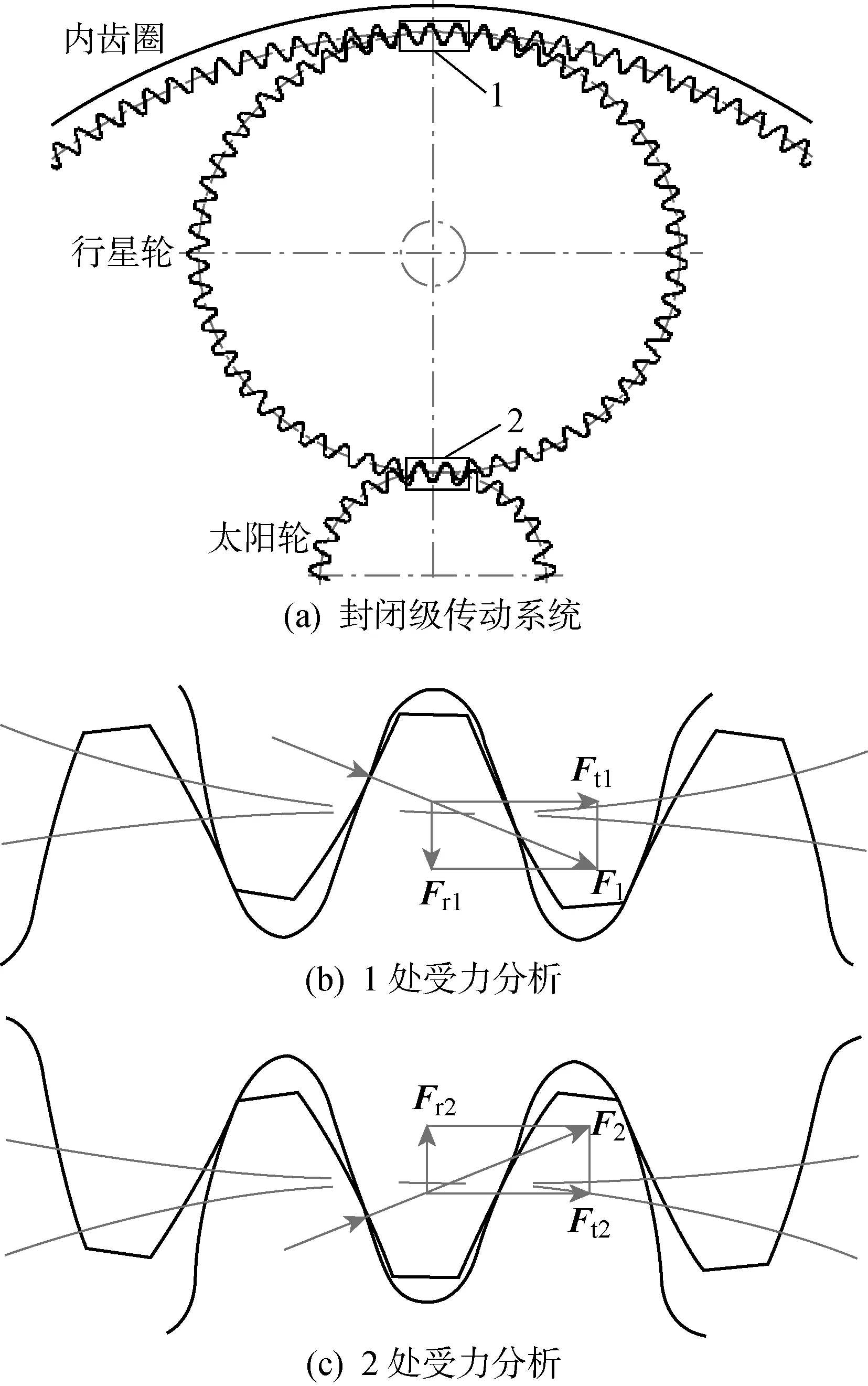
图3 齿轮受载示意图Fig.3 Diagram of gear loading
(17)
式中:Mw为内齿圈转矩;n为行星轮个数;m为太阳轮(行星轮)模数;zw为内齿圈齿数.
2 柔性销轴试验仿真
2.1 有限元模型的建立
2.1.1几何模型 以理论计算获得的销轴结构过盈配合情况下的最大弯曲载荷、应力应变和过盈量为数值基础设计销轴结构模型,选择缩小比例为1∶5的试件进行试验与仿真,加载载荷比例取 1∶25,试件的配合公差(H7/u6)与原模型相同.比例模型的尺寸示意图如图4所示.
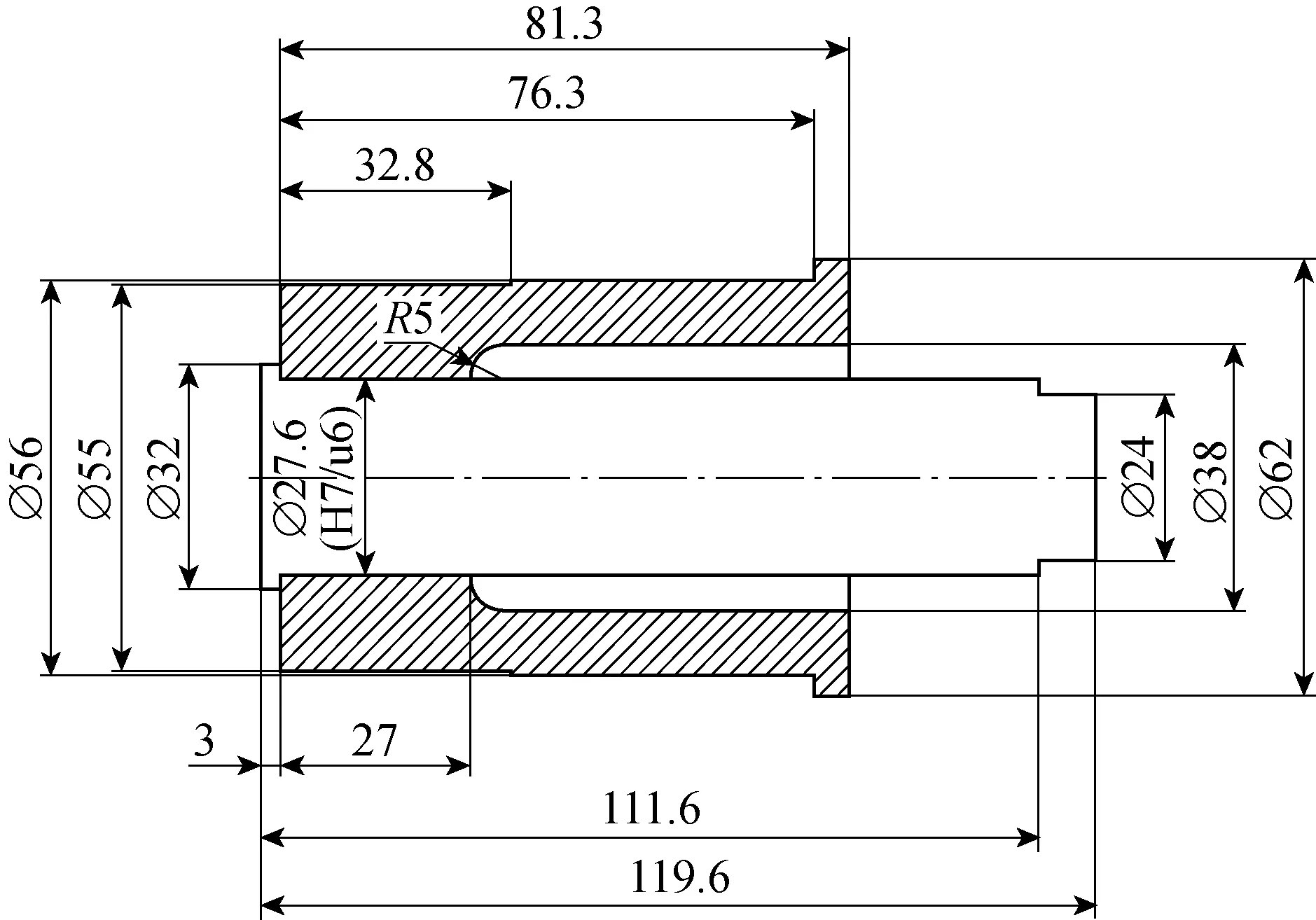
图4 比例模型的尺寸示意图(mm)Fig.4 Size diagram of scale model (mm)
2.1.2有限元模型 由于在环向上柔性销轴模型的应力应变是一致的,且单一方向上的弯曲载荷在两个半剖面的作用结果相同,所以在有限元分析中为了节省计算资源和时间,将销轴结构半剖面三维模型作为分析模型.
为保证计算精度及结果收敛性,将三维模型导入Abaqus软件中进行区域分割,再输入不同的弹性模量和泊松比,以此来实现渗碳层与未渗碳层的划分,而渗碳层深度的变化则通过改变分区厚度来实现,模型区域分割示意图如图5所示.

图5 模型区域分割Fig.5 Model area segmentation
采用Abaqus/Standard求解器模块创建周期性幅值曲线,定义幅值曲线参数设定弯曲载荷大小;销轴结构过盈配合属于边界非线性问题,可通过调节接触位移数值来改变柔性销轴过盈配合的过盈量.
440C高碳高铬马氏体不锈钢锻件是公司承接的某公司用轴承应力环锻件。两批次锻件的理化试样在长时间退火后进行淬火,在淬火冷却过程中和冷处理过程中均出现了开裂现象。为找出断裂失效原因,对淬裂样件进行了分析检测。
之后进行网格划分,非接触区域网格进行粗化,接触区域网格适当细化.网格单元选用四面体单元C3D4和线性减缩积分单元C3D8R,细分单元的最小边长为 0.90 mm.柔性销轴模型共有单元 125 334 个,节点104 630个;套筒模型共有单元83 447个,节点73 957个,如图6所示.
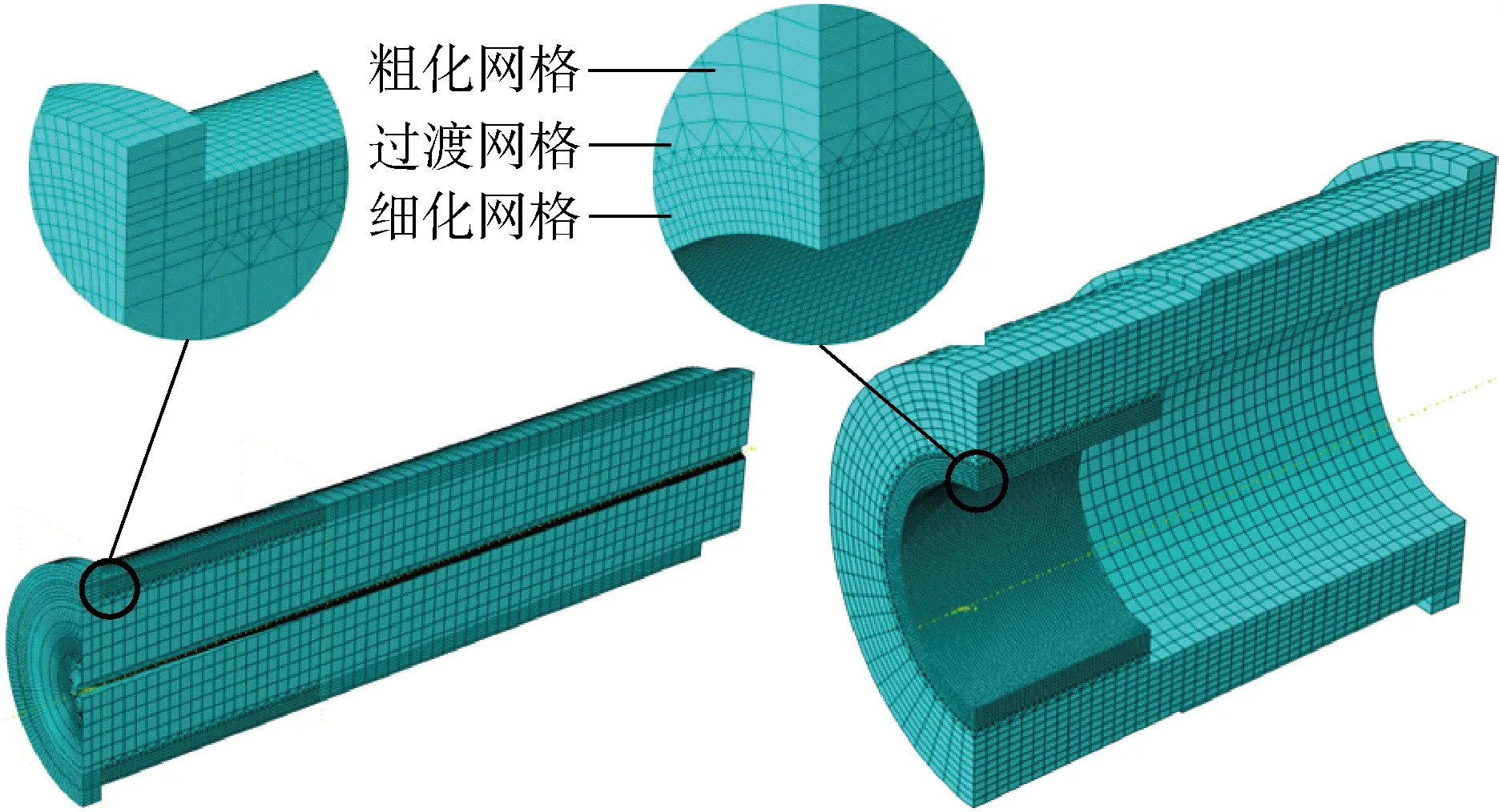
图6 仿真模型网格划分Fig.6 Mesh generation of simulation model
将销轴与套筒两者之间的关系设置为面-面接触,主面为套筒内环面,从面为销轴环面,接触属性为“硬接触”.比例模型的约束和受载情况与实际工况基本相同,把x、y、z方向上的全约束施加到销轴模型的尾端,把x方向的转动约束和位移添加到销轴的剖分截面上,其位移与载荷的边界定位约束,如图7所示.
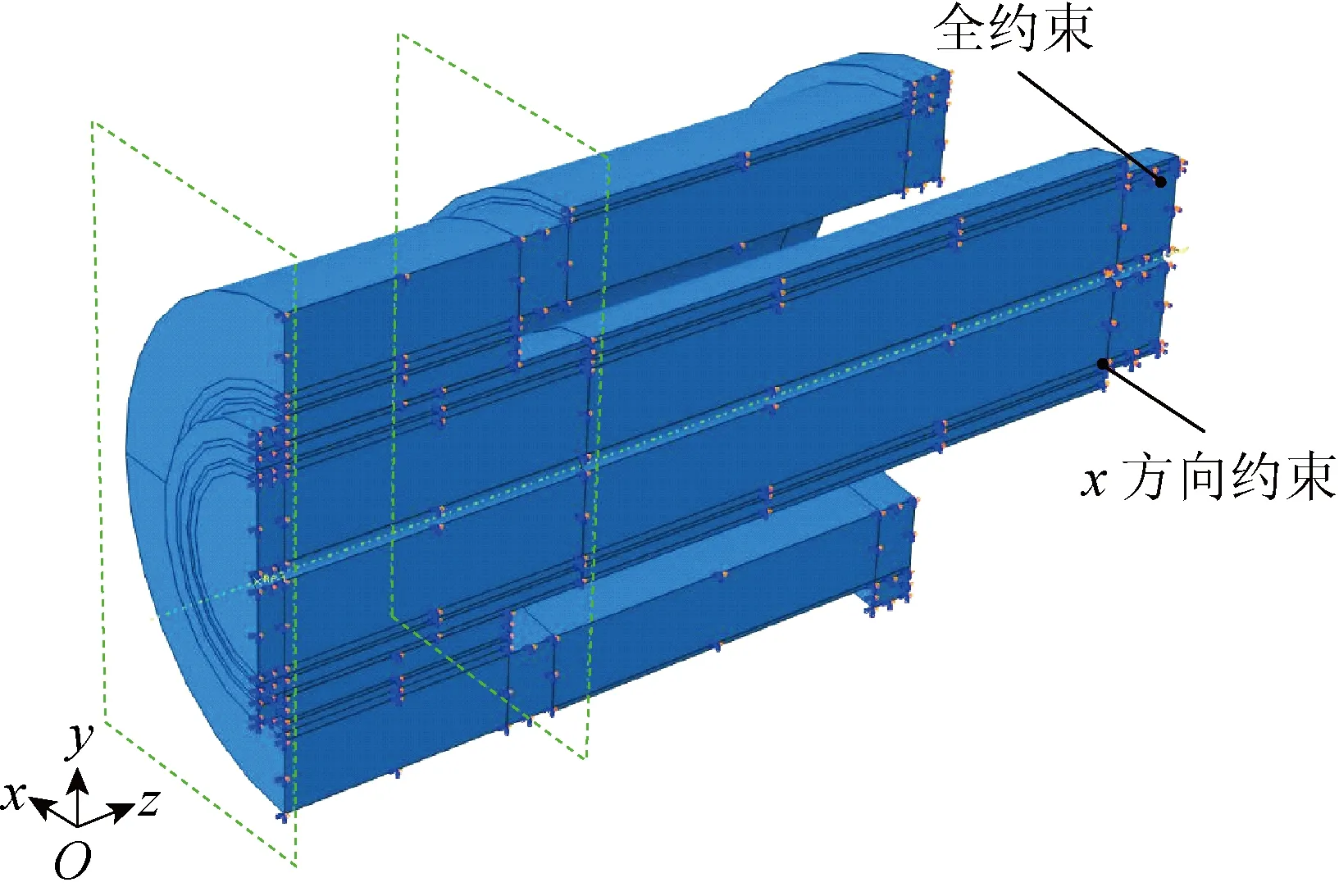
图7 模型边界约束Fig.7 Model boundary constraints
2.2 有限元计算结果与分析
在齿轮增速箱的载荷谱中,齿轮传动传递的转矩T分别为4.48×105、9.60×105、1.408×106、1.856×106、2.325×106N·m,根据式(17)可得施加于销轴结构试件上的弯曲载荷分别为 5.559、11.912、17.471、23.030、28.854 kN;根据式(13)及(16)确定过盈量的最大有效值,并以0.005 mm为梯度的递增数值进行仿真;根据渗碳工艺要求取0.2~1.0 mm的渗碳层深度值.
设置构件的弯曲载荷为 17.471 kN、公差为H7/u6条件下的过盈量为0.030 mm、渗碳层深度为0.6 mm作为基准参数,应用Abaqus软件模拟分析以上不同因素下接触应力、摩擦剪切力以及滑移幅值的变化规律.
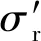
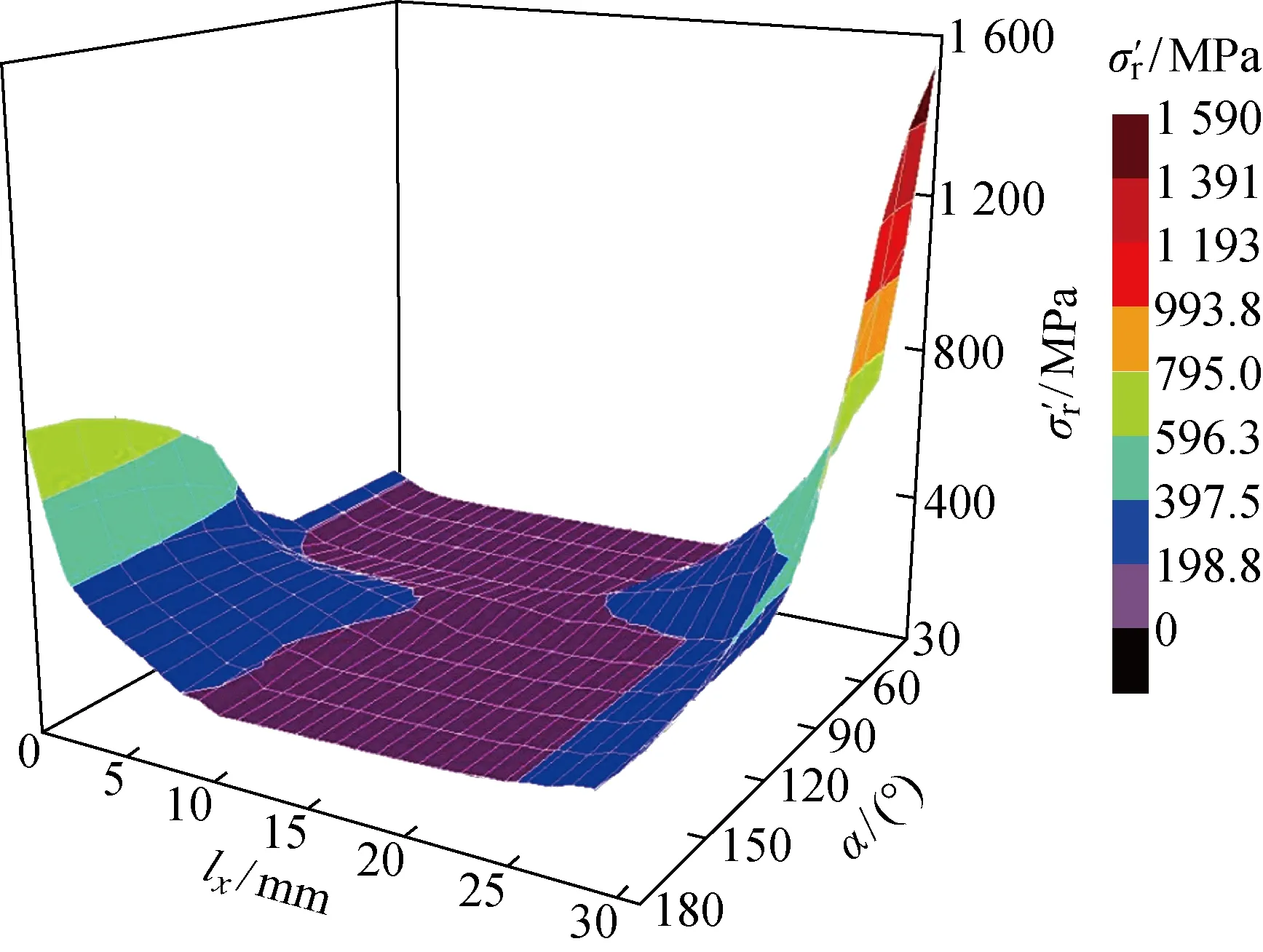
图8 模型中接触应力的分布Fig.8 Distribution of contact stress in model
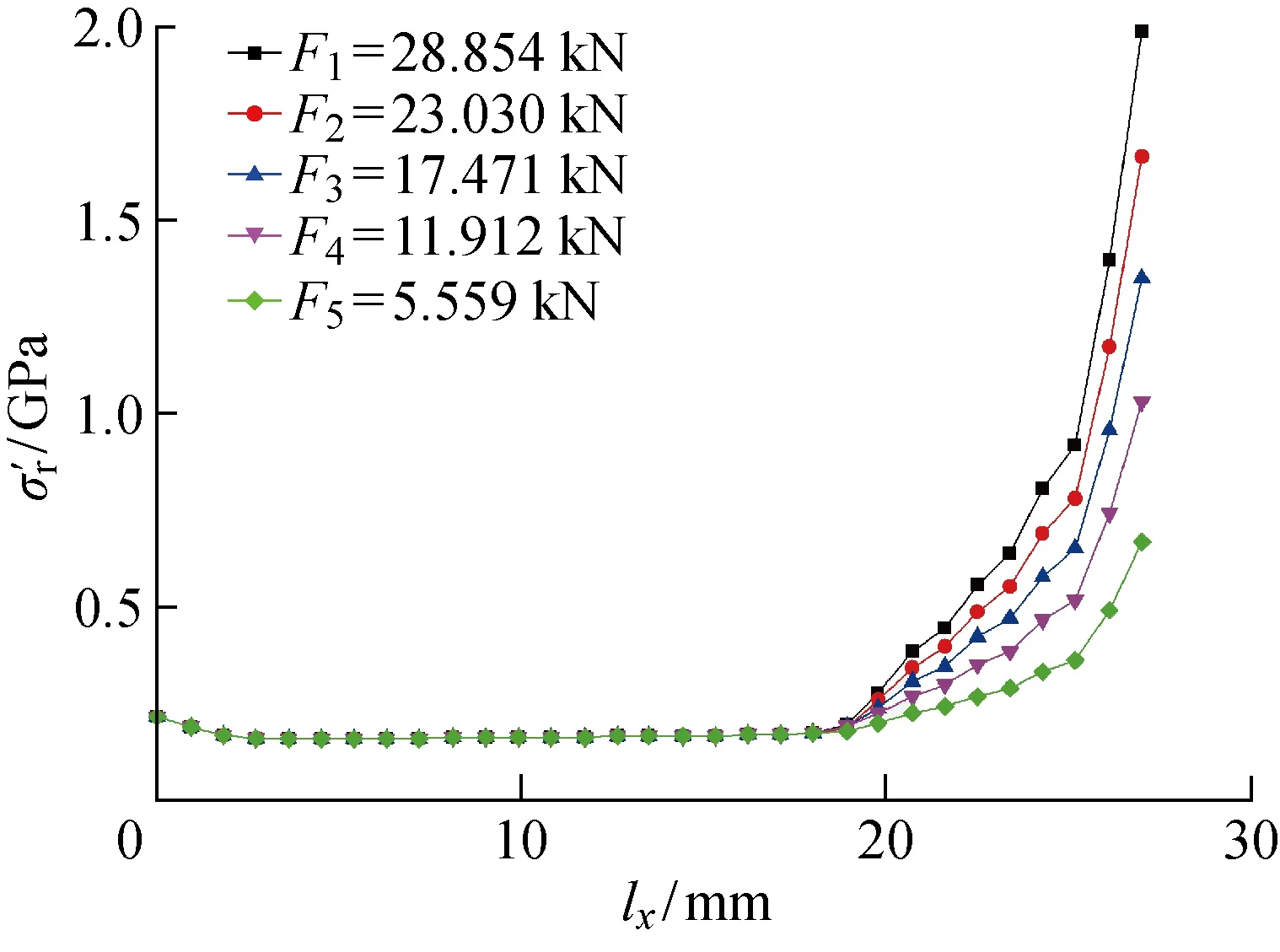
图9 接触应力与弯曲载荷的关系Fig.9 Contact stress versus bending load
接触应力与弯曲载荷Fi(i=1,2,…,5)的关系如图9所示,接触边缘区域为弯曲载荷对接触应力影响最大的区域.弯曲载荷作用时,轴向距离为0~18 mm处的接触应力基本不会发生改变;轴向距离大于18 mm时(接近加载源),应力则开始逐渐变大,边缘处出现较大的应力峰值,且随着载荷的增加,边缘应力集中的现象愈加剧烈.
接触应力与过盈量δi(i=1,2,…,5)的关系如图10所示.在保持其他条件相同而过盈量取值以0.005 mm的梯度递增情况下,接触应力以每梯度29 MPa的增量与δ成线性关系.可见过盈量不同时,接触应力的变化趋势基本相同,且δ对边缘应力集中情况的影响较小.
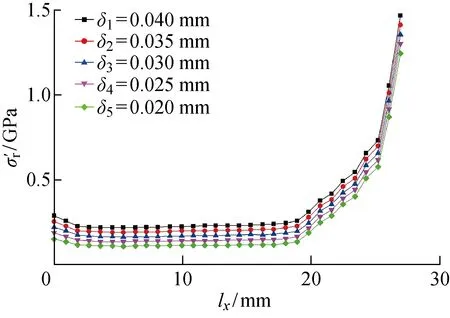
图10 接触应力与过盈量的关系Fig.10 Contact stress versus interference
接触应力与渗碳层深度hi(i=1,2,…,5)的关系如图11所示.当渗碳层深度不同时,接触应力几乎不会发生变化,且接触应力的变化趋势基本相同,深度变化对接触应力产生的影响较小.
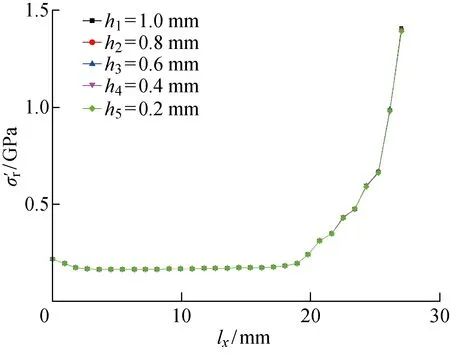
图11 接触应力与渗碳层深度的关系Fig.11 Contact stress versus depth of carburized layer
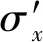
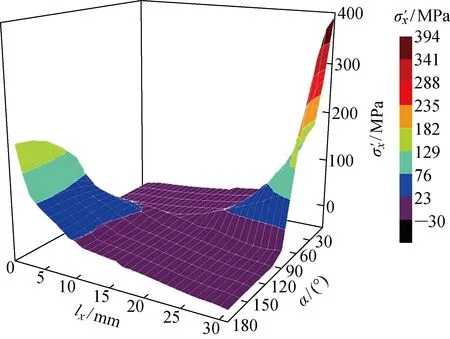
图12 模型中摩擦剪切应力的分布Fig.12 Distribution of frictional shear traction in model
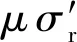
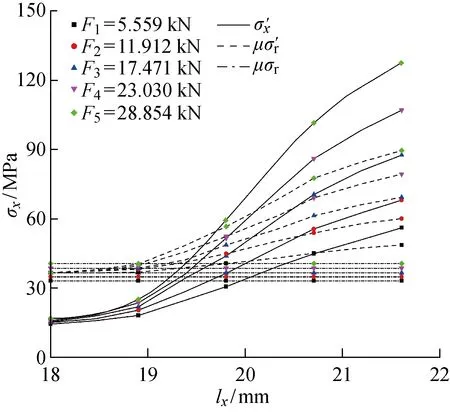
图13 摩擦剪切应力与弯曲载荷的关系Fig.13 Frictional shear traction versus bending load
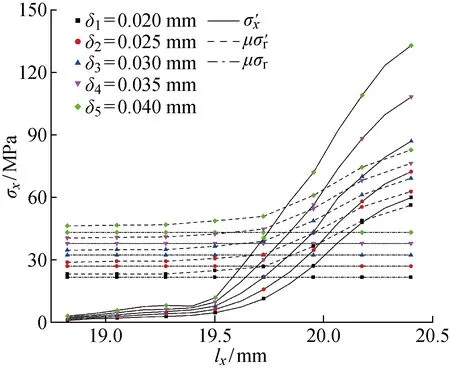
图14 摩擦剪切应力与过盈量的关系Fig.14 Frictional shear traction versus interference
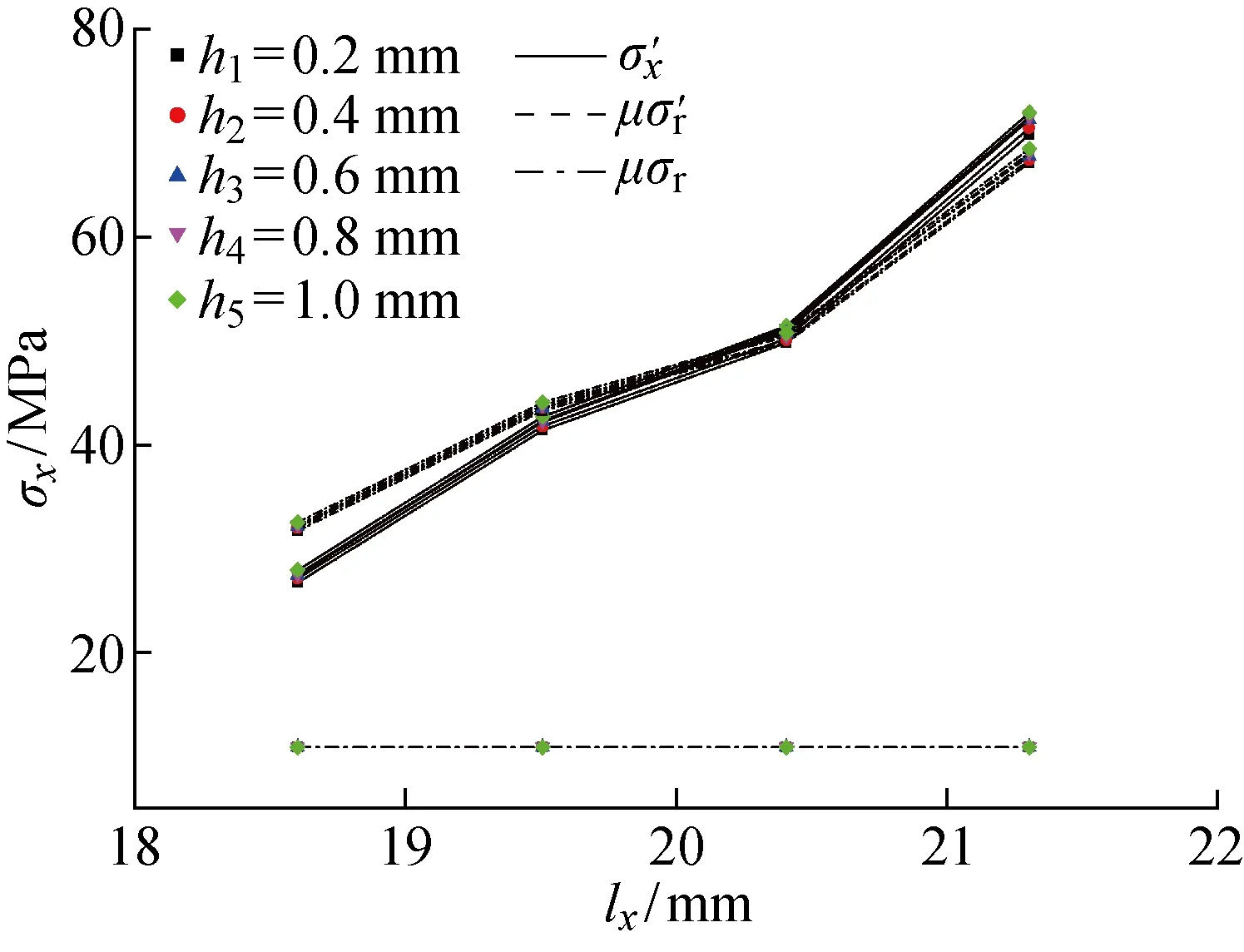
图15 摩擦剪切应力与渗碳层深度的关系Fig.15 Friction shear traction versus depth of carburized layer
由图13~15可知,弯曲载荷和过盈量的变化对摩擦剪切应力的影响都较大,而渗碳深度的变化则几乎无影响.
2.2.3各参数对滑移幅值的作用探究 模型中滑移幅值的分布如图16所示,其中LF为过盈配合表面的滑移幅值.上半面(环向角度0°~90°)距加载源较远处的滑移幅值小于距其较近处,下半面(环向角度90°~180°)距其较远处产生了幅值上升的情况.模型中,在滑移几率最大的轴线上取点用以表征滑移幅值的影响,如图17~19所示.
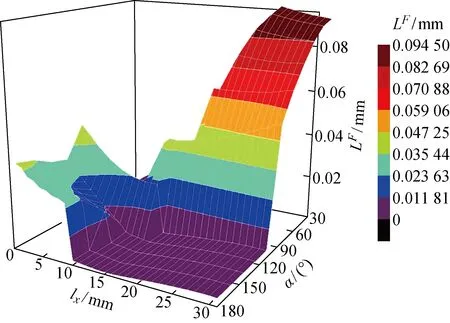
图16 模型中滑移幅值的分布Fig.16 Distribution of slip amplitude in model
滑移幅值和弯曲载荷的关系如图17所示.当弯曲载荷增加时,过盈配合部位的最大滑移幅值也会增大,尤其在接触边缘区域,最大滑移幅值与弯曲载荷近似呈正比关系.滑移幅值和过盈量的关系如图18所示.当过盈量增大时,过盈配合接触表面的最大滑移幅值有所增大.但过盈量的改变对最大滑移幅值的影响不大.渗碳层深度对滑移幅值影响如图19所示.渗碳层深度对滑移幅值所产生的影响很小,只在接触边缘区域约有1.7 μm的增量.
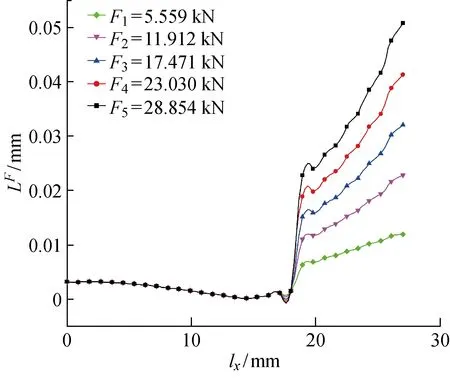
图17 滑移幅值和弯曲载荷的关系Fig.17 Slip amplitude versus bending load
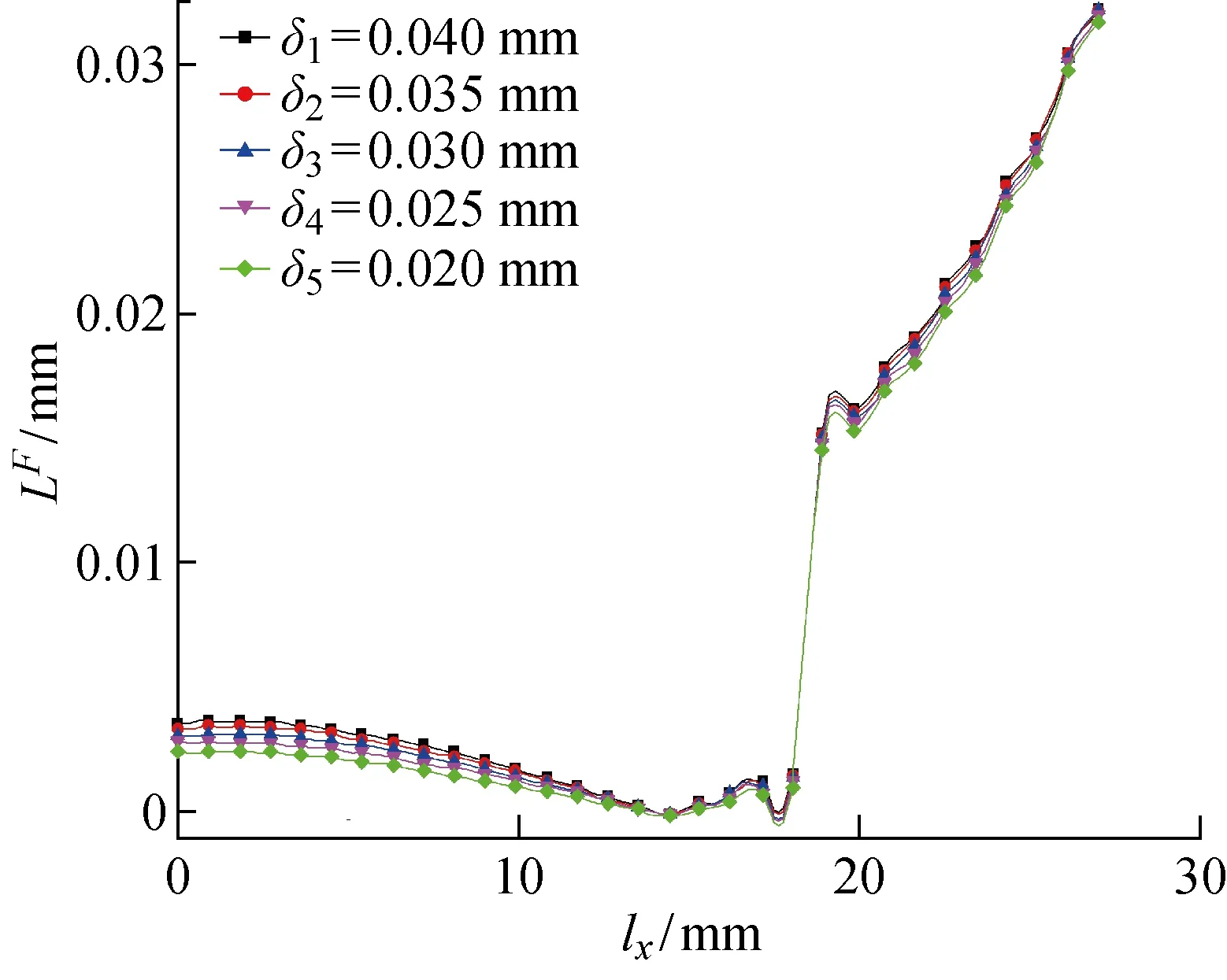
图18 滑移幅值和过盈量的关系Fig.18 Slip amplitude versus interference
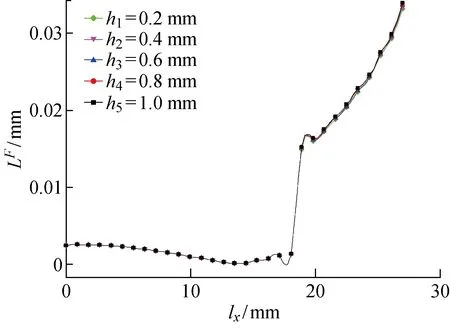
图19 渗碳层深度对滑移幅值影响Fig.19 Effect of depth of carburized layer on slip amplitude
由图17~19可知,在距离加载源0~18 mm的位置(0位置为最远),弯曲载荷和过盈量对滑移幅值的影响都非常小,在18 mm以外的位置,弯曲载荷对滑移幅值的影响程度明显大于过盈量.渗碳层深度对滑移幅值影响全程都较弱.
2.2.4过盈配合柔性销轴的寿命预测 采用SWT法[15]预测柔性销轴的微动疲劳寿命,表达式为
(18)
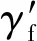
将获得的不同因素数值下的寿命数据制成预测疲劳寿命S-N曲线如图20所示,其中N1为预测疲劳寿命.
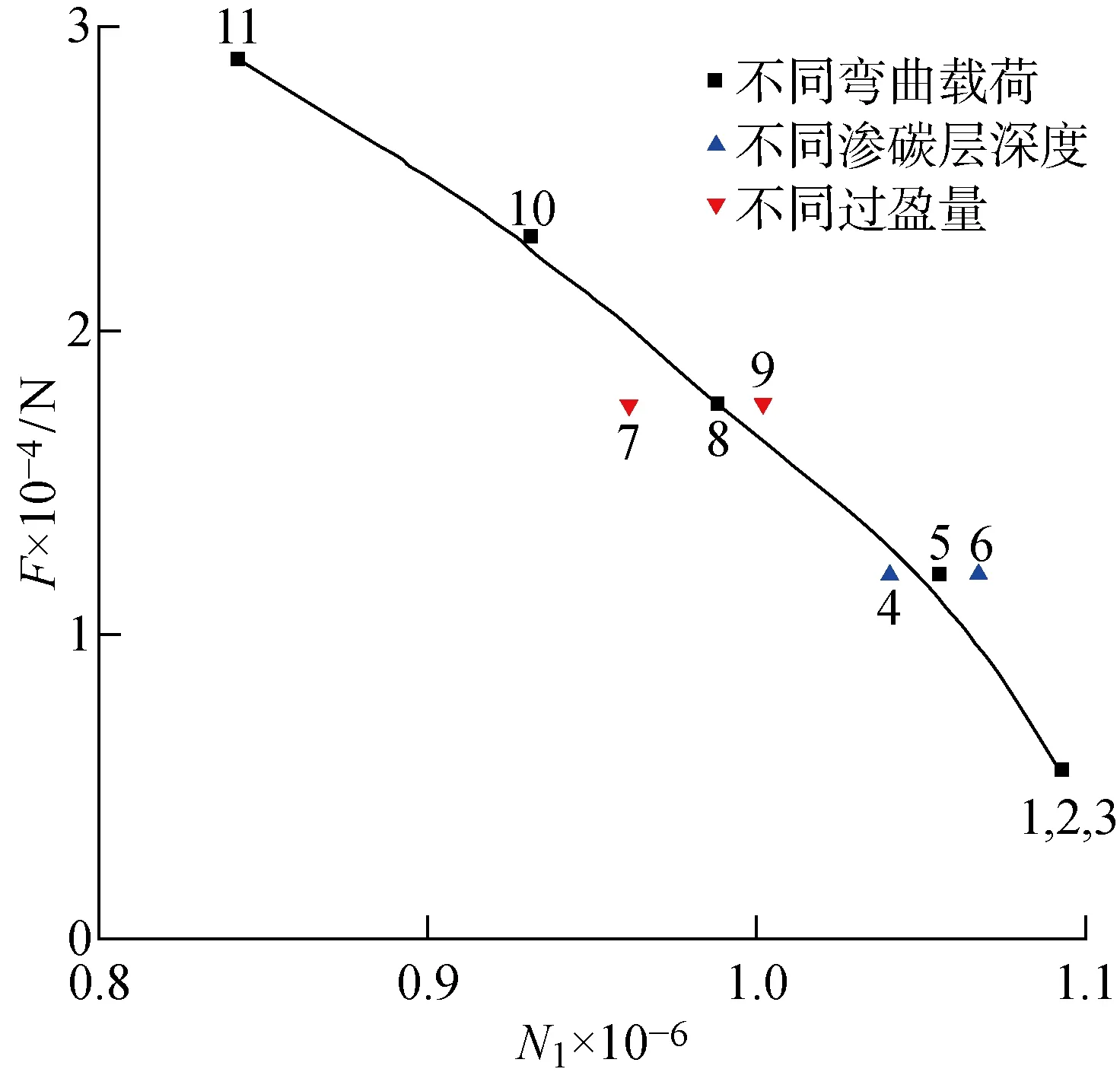
图20 临界平面法预测S-N曲线Fig.20 Predicted S-N curve of SWT method
由图20可知,当其他影响因素保持不变时,微动疲劳寿命随着弯曲载荷的增大而降低,且降幅非常明显.以上现象是由于当弯曲载荷增加时,滑移幅值及接触应力急剧增长,削弱了销轴结构的疲劳寿命导致的.当弯曲载荷保持不变时,微动疲劳寿命随着过盈量的增大而降低,这主要是因为当过盈量增大时,柔性销轴过盈配合表面的应力应变也随之增大,虽然增幅较小但也会削弱微动疲劳寿命.渗碳层深度的变化对过盈配合表面的应力应变影响很小,所以渗碳层深度的变化对疲劳寿命几乎没有影响.
3 柔性销轴微动疲劳试验
3.1 试验方案
选取岛津EHF系列疲劳试验机进行弯曲载荷加载,此试验机通过设定作动器行程幅差可在试样报废时及时停止加载并显示当前循环次数,此次数记为微动疲劳寿命,如图21(a)所示.也可通过观察试样尾部的磨损来确定试样的报废与否,当表面有磨屑喷溅且有较明显的氧化圈出现或可听到刺耳的摩擦声时(此时柔性销轴滑脱),试样报废,此时系统显示的次数即记为微动疲劳寿命,如图21(b)所示.
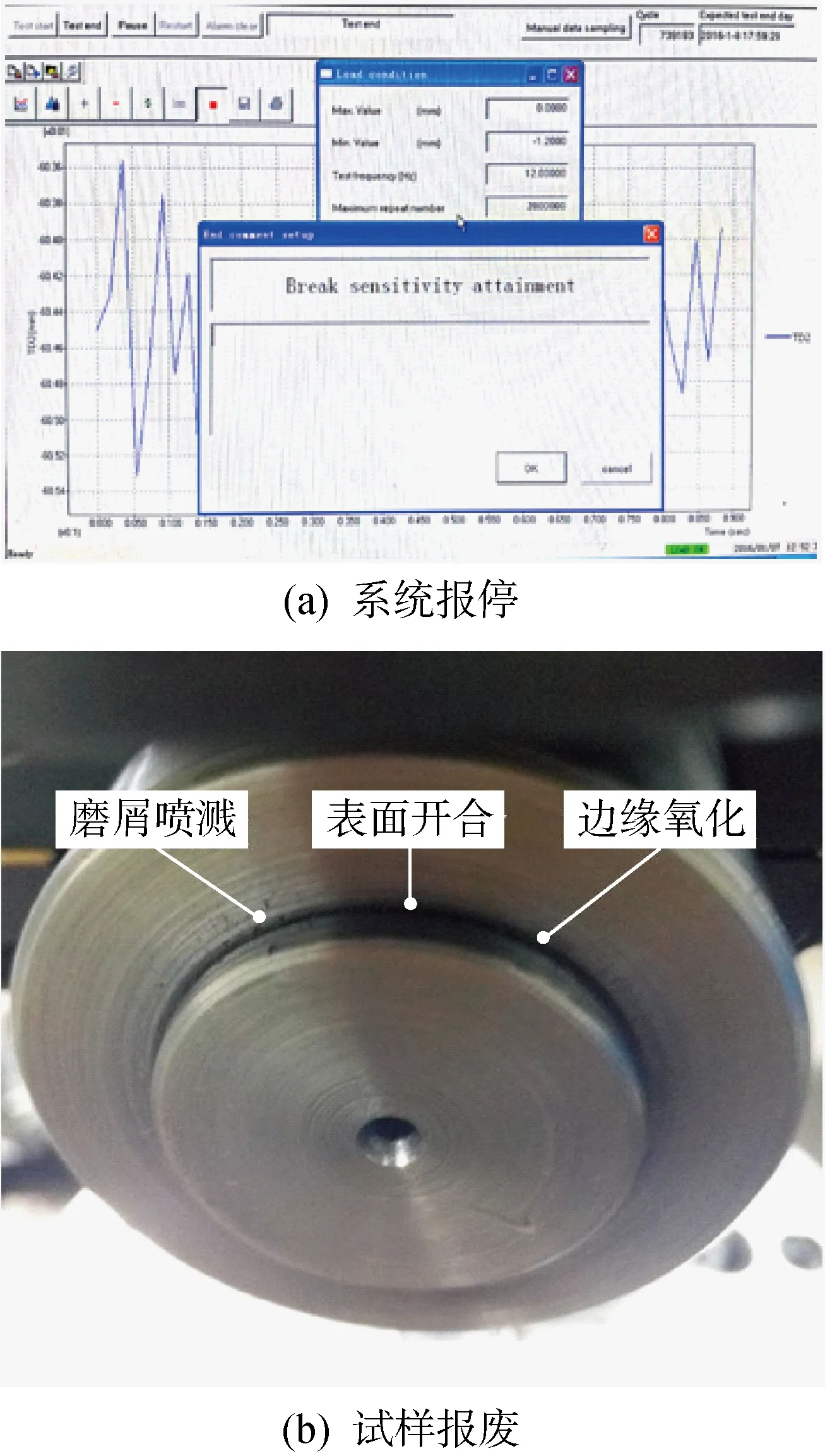
图21 试样报废标准Fig.21 Standard of sample abandonment
销轴和套筒的材料分别选用18CrNiMo6和42CrMo,与实际工程应用中使用的材料相同.将销轴尾端适当加长以保证柔性销轴结构的安装与加载.试验后记录寿命数据并绘制微动疲劳S-N曲线,观测不同因素下试件的微动疲劳微观损伤形貌,比较其表面破坏程度,研究不同因素对柔性销轴寿命的作用及损伤机理.试件加载结构和柔性销轴夹具结构如图22和23所示.

图22 试件加载结构Fig.22 Structure of specimen loading
采用三因素四水平试制了11组试件开展试验,柔性销轴试样如图24所示.其中:最小弯曲载荷为5.559 kN;最大弯曲载荷为 28.854 kN;最小过盈量为0.02 mm;最大过盈量为0.039 mm;渗碳层深度为0.2~0.6 mm;通过随炉试件检测渗碳层深度.

图23 柔性销轴夹具结构Fig.23 Structure of flexible pin clamp

图24 柔性销轴试样Fig.24 Flexible pin specimen
3.2 试验微动疲劳寿命结果分析
柔性销轴试验的S-N曲线如图25所示,其中N2为试验疲劳寿命.该曲线可以反映微动疲劳寿命随弯曲载荷、过盈量、渗碳层深度等因素的变化规律,此规律能够代表各因素对疲劳寿命的影响程度,研究柔性销轴在寿命方面的微动疲劳特性.在其他参数保持不变的情况下,试件的疲劳寿命随弯曲载荷的增加而迅速降低.当F=5.5 kN时,疲劳破坏基本不会发生(考虑到时间限制,试验加载次数最多为106次);当F<18 kN时,疲劳寿命可达9×105次;当F>15 kN时,微动疲劳寿命的下降幅度急剧变大.而当其他影响因素保持不变、过盈量增大时,微动疲劳寿命随之减小.当渗碳层深度增加时,微动疲劳寿命变化较小,即对疲劳寿命的影响较小.
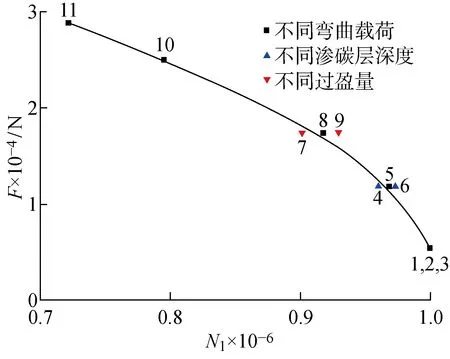
图25 柔性销轴试验的S-N曲线Fig.25 S-N curve of flexible pin test
SWT模型预测与试验疲劳寿命的对比如图26所示.虽然数据较分散,且由于装配误差及材料缺陷等原因,使得试件的试验疲劳寿命小于预测寿命,但是试验数据分布在3倍误差带范围内,这表明SWT模型预测的微动疲劳寿命与试验微动疲劳寿命的吻合度较高.又由于SWT公式中的参数来自于Abaqus仿真模型,所以同时证明了仿真与试验相结合的研究手段是可行性的.
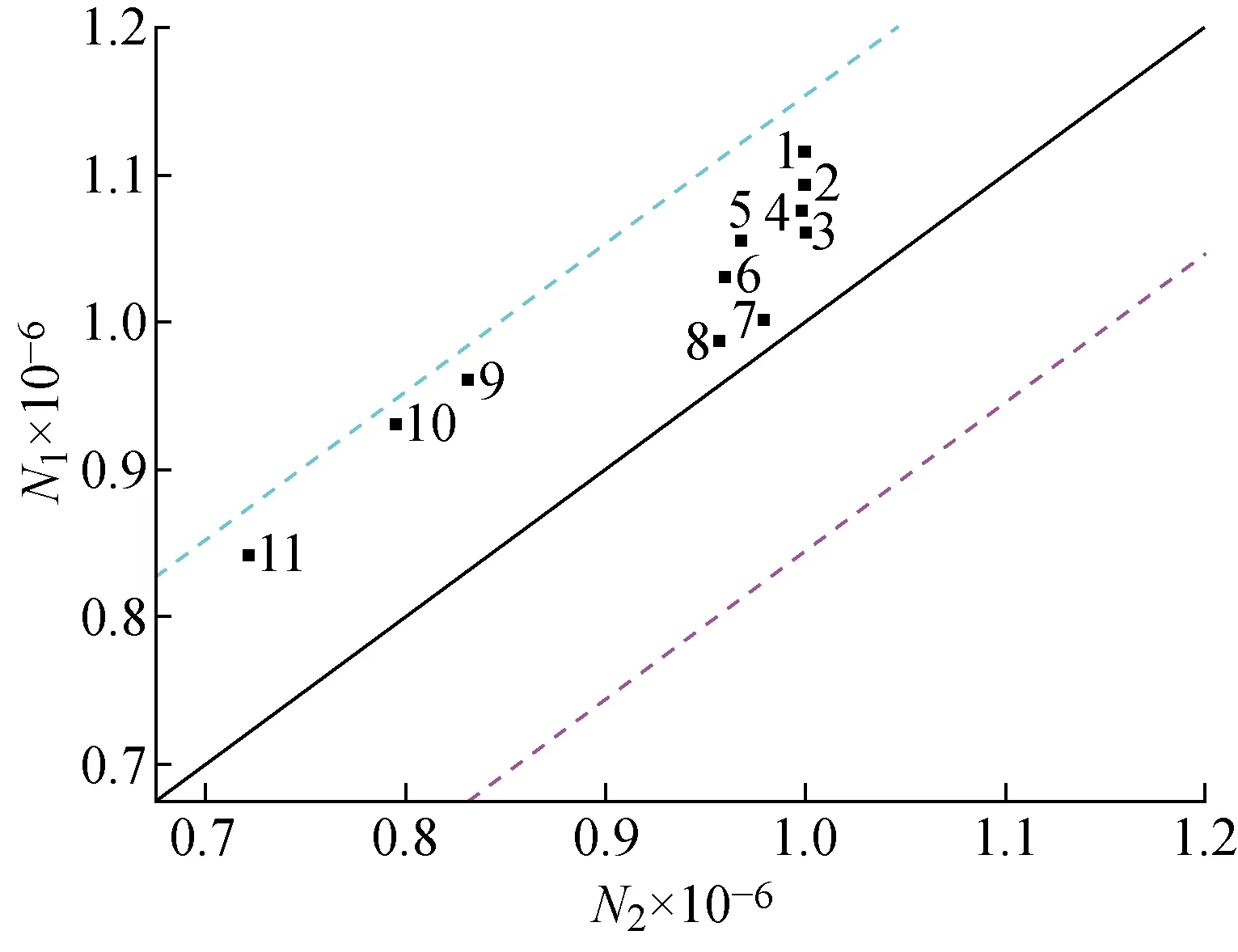
图26 SWT模型预测与试验疲劳寿命对比Fig.26 Comparison of fatigue lifes between SWT model prediction and test data
3.3 微动形貌分析结果及讨论
套筒材料18CrNiMo6的抗磨性能远低于销轴材料42CrMo,所以销轴的损伤程度小于套筒的损伤程度.由仿真结果可知,对于接触应力、摩擦剪切应力和滑移幅值,距加载源较远处的数值均远小于距其较近处的数值.故在轴套上选择距加载源最近的区域进行形貌观测分析.
3.3.1弯曲载荷对微动形貌的影响 在柔性销轴微动疲劳试验中,不同加载情况下损伤的形貌大体类似,总体上观察均为“C”型弧面.如图27所示.由图27可知,主要损伤形式为微动磨损的A区为完全滑移区,其位于“C”型弧面右侧且靠近加载端;主要损伤形式为微动磨损和疲劳裂纹的B区为混合区,其位于“C”型弧面中间;位于弧面左边且靠近固定端的C区为黏着区,其主要损伤形式为轻微微动磨损,即使萌生少许裂纹也只发生在高周微动磨损附近,靠近与混合区的分界线.加载端的接触表面承受交变应力会产生较大的位移幅值,而固定端由于套筒的弹性变形则会产生较小的位移幅值,所以靠近固定端处C区的损伤情况最为轻微.为探究不同弯曲载荷下试件的微动疲劳损伤情况,选取载荷工况为 5.559、17.471 及 28.854 kN的试件对其表面形貌进行高倍放大观测.
当F=5.559 kN时,此部位处于黏着状态,接触表面基本不会发生相对滑动,混合区和完全滑移区的磨损较小,并未出现明显的“C”型弧面磨斑(见图27(a)).当F=17.471 kN时的微动损伤形貌如图28所示.由图28可知,“C”型磨斑形貌初步形成,A区和B区的范围变大,但A区范围仍相对较小,磨损情况变得严重(见图27(b)).如图28(a)所示,位于“C” 型磨斑左侧的损伤带显现出塑性变形造成的不间断的“波浪纹”和十分清晰的材料滑移堆叠现象,这种现象是由于此区域接触应力较大但位移幅值较小,难以释放材料的变形能,累积了很大的塑性变形导致的.损伤带产生塑性流动现象,导致了塑性流动凹槽的形成.如图28(b)所示,一定数目和规模的片状材料和磨粒剥落出现在A区内,范围大且数量多,反映了微动疲劳磨损的剥层机制.

图28 当F=17.471 kN时的微动损伤形貌Fig.28 Fretting damage morphology at F=17.471 kN
当F=28.854 kN时的微动损伤形貌如图29所示.此时,加载端接触表面的位移幅值变大,A区和B区的特征已非常明显,且A区范围增大,出现了非常严重的磨损情况(见图27(c)).这是由于A区内出现了非常严重的冷作硬化,颗粒被整体剥落,且张开区明显开合,氧气进入其中,所以出现严重的磨损情况,如图29(a)所示.B区的磨损情况同样严重,随着弯曲载荷加载次数的增加,不间断的凹槽随之形成,塑性变形区域随之变大,并伴随有大量的磨屑以及片状剥落的情况出现,疲劳裂纹开始在剥落区域边缘大面积萌生,如图29(b)所示.

图29 当F=28.854 kN时的微动损伤形貌Fig.29 Fretting damage morphology at F=28.854 kN
试验结果表明,在其他影响因素保持不变的情况下,当弯曲载荷增大时,靠近加载源的完全滑移区(A区)的范围变大,磨损情况变得严重,这是因为磨屑剥落且无法排出,在接触应力的作用下导致了片状剥落的情况,A区几乎完全磨损;混合区(B区)也会出现较明显的磨损情况,疲劳裂纹在此区域萌生并扩张;而距离加载源最远的C区范围变小,其磨损情况相对轻微.当F增大时,过盈配合表面的损伤情况变得更为严重,并且有大面积裂纹产生及扩张.由此可知,弯曲载荷是疲劳损伤的重要影响因素.为减弱微动疲劳的影响,降低柔性销轴的受载力,应尽可能增大零部件之间的配合精度.
3.3.2过盈量对微动形貌的影响 在柔性销轴微动疲劳试验中,当其他因素保持不变时,过盈量不同的柔性销轴加载后的疲劳损伤程度差异不大.为研究δ的变化对疲劳损伤的影响,分别取δ=0.022,0.037 mm时的试样对其表面形貌进行高倍放大观测.
过盈量变化对试件损伤的情况如图30所示.从全貌上看,过盈量不同的试件的主要区别为B区“波浪纹”的宽度以及A区的磨损程度.在B区内,δ的增加导致了接触应力的增大,但位移幅值较小,难以释放材料的变形能,累积了较大的塑性变形,进而因塑性变形产生“波浪纹”状材料堆叠景象,并且δ增大时堆叠现象产生的“波浪纹”愈加可观,如图31所示.当δ递增时,B区萌生出几乎与竖直方向垂直的疲劳裂纹,并且其数目在不断增加,如图32所示.之后,由于摩擦剪切应力的影响,疲劳裂纹沿切向扩张,如图33所示.裂纹扩张的程度随着δ的增加而愈加严重,另外衍生裂纹数量有所增加.如图34所示.综上所述,过盈量的递增也会加重过盈配合表面的磨损情况.

图30 过盈量变化下试件磨损的全貌图Fig.30 Overall wear view at different interferences

图31 材料滑移与堆叠的微动损伤形貌Fig.31 Fretting damage morphology of slip and stack of materials

图32 裂纹横向萌生的微动损伤形貌Fig.32 Fretting damage morphology of crack initiation

图33 裂纹纵向扩展的微动损伤形貌Fig.33 Fretting damage morphology of longitudinal crack propagation

图34 磨粒氧化磨损的微动损伤形貌Fig.34 Fretting damage morphology of oxidation wear of abrasive particles
试验结果表明,当过盈量增加时,裂纹更易产生且其扩展速率变大,A区内的磨损情况也愈加严重,加重了过盈配合表面的微动磨损.尽管过盈量的变化对疲劳损伤的作用不大,但为减轻销轴的损伤程度,可在最小过盈量(见式(13))至最大过盈量(见式(16))范围内适当减小柔性销轴的过盈量,此范围内选取的过盈量保证了载荷的有效性和结构的强度要求.
3.3.3渗碳层深度对对微动形貌的影响 渗碳层深度的变化会导致试验后过盈配合表面的微动疲劳损伤情况不尽相同,如图35所示.研究h对试件的影响时,分别选取h=0.4,0.6 mm的试件对其表面形貌进行高倍放大观测.

图35 渗碳层深度变化的磨损全貌图Fig.35 Overall wear view at different depths of carburized layer
渗碳层深度不同的试件的区别主要表现为A区及B区损伤情况的差异.由于弯曲载荷的加载,A区产生一定数量且无法排出的磨屑,并由此产生磨粒层,循环加载时磨粒层会大范围脱落,而渗碳层深度越大,销轴结构高耐磨度的渗碳层厚度就越大,试件抗磨损能力越大,较难出现剥落情况或仅会出现轻微的剥落情况,如图36所示.在B区内,磨粒层剥落之后,裂纹极易萌生的区域在边缘形成,此区域在接触应力与摩擦剪切力的共同作用下非常容易产生疲劳裂纹,而渗碳层深度增大时磨损和剥落情况会得到减轻,疲劳裂纹的产生得到抑制,所以渗碳层深度的增加也减轻了B区的疲劳损伤情况,如图37所示.

图36 片状剥落磨损的微动损伤形貌Fig.36 Fretting damage morphology of flake wear

图37 裂纹萌生扩展的微动损伤形貌Fig.37 Fretting damage morphology of crack initiation and propagation
试验结果表明,随着渗碳层深度的增加,A区内的材料剥落情况有所缓解,B区裂纹萌生及扩张的概率降低.虽然渗碳层深度的变化对疲劳损伤的作用比较轻微,但为减轻过盈配合表面的疲劳损伤程度,可在条件允许的情况下适当增大渗碳层深度.
4 结论
(1) 对柔性销轴进行了数值仿真和试验,结果表明:销轴与套筒的接触边缘区域存在很大的应力梯度和应力集中;弯曲载荷增大时,滑移幅值、接触应力及摩擦剪切应力也随之增大;过盈量增大时,过盈配合接触表面的应变应力变化规律大致相同,对边缘现象应力集中情况的作用较小;渗碳层深度几乎不会对应力应变产生影响.
(2) SWT模型预测的微动疲劳寿命与试验微动疲劳寿命吻合度较高,仿真与试验相结合的研究手段具有合理性.疲劳寿命受弯曲载荷影响最大,过盈量次之(过盈量的增加会造成疲劳寿命在一定程度上的减小),渗碳层深度最小.弯曲载荷的增大使得过盈配合接触表面的疲劳损伤情况愈加严重,完全滑移区内的微动磨损和混合区内的裂纹萌生扩张是其主要损伤方式,并且疲劳寿命随着弯曲载荷的增加而迅速降低.过盈量增加时,接触表面的磨损程度变大,疲劳寿命随之减小.渗碳层深度的增加使得接触表面的抗磨损能力得到提升,也降低额裂纹萌生扩张的概率,因此疲劳寿命有所增大.
(3) 可通过提高行星传动系统的加工精度,减小弯曲载荷冲击,在一定范围内减小柔性销轴的过盈量及增大渗碳层深度等措施降低柔性销轴疲劳损伤程度,延长其工作寿命.
(4) 研究成果可以并已用于企业的产品研发,用于指导工程设计,解决工程中的实际应用问题.
