自主水下机器人强制自航下潜的类物理模拟

吴利红，封锡盛，叶作霖，李一平

(1.大连海事大学 船舶与海洋工程学院，辽宁 大连 116026；2.中国科学院沈阳自动化研究所 机器人学国家重点实验室，沈阳 110016)

自主水下机器人(AUV)、潜艇通常需要快速下潜到一定深度执行任务，精确预报这种下潜过程有助于对载体的航行轨迹和安全性进行有效控制.模型试验和数值仿真是进行载体下潜操纵性预报的主要方法.限于水池有限空间尺度，AUV下潜试验通常在海试中进行，增加了风险.传统数值仿真方法是求解基于水动力系数的泰勒展开的载体操纵性方程来预报垂直面操纵运动.这种方法通过模型试验、数值模拟、面元法等获得载体水动力系数，量化载体控制面(包括舵翼)和螺旋桨的作用力和力矩，并作用于载体上，在MATLAB中的Simulink平台中或VC平台中实现载体离线的无动力螺旋下潜或垂直下潜的操纵运动预报，获得载体的运动轨迹、姿态、受力等量化参数[1-3].该方法无需建立载体几何模型和求解流场，计算速度快.不足之处在于：① 较适用于以载体纵轴为主航行方向，其他方向运动较小的运动形式；② 运动受限于水动力系数对应的试验运动；③ 无法获得载体的流场特征，无法探求物体运动响应的内在因素.

随着计算流体力学软件和硬件技术的发展，采用类物理数值模拟方法进行载体自航操纵运动变得可能.这种操纵运动预报方法是直接建立载体带舵翼和螺旋桨的全附体模型，求解流体动力学方程，实时获得载体的受力、运动，能获得详细的操纵运动流场特征.目前可以采用重叠网格法和动网格法进行这种类物理数值模拟，如文献[4-7]采用重叠网格法对水面船舶和潜艇的自航操纵运动、z型操舵运动、波浪中的纵倾运动和水平面的回转运动进行了数值模拟.

相对于重叠网格，动网格法是较早用于求解边界移动的一种方法，如对航空飞行器的武器分离仿真[8-9]，水下载体分离仿真如AUV 从鱼雷管发射[10]和AUV水下对接[11].但是动网格在边界移动时，常导致边界附近流域的网格拉伸或压缩比例失调，导致网格畸变，网格质量变差，数值精度降低，甚至导致网格出现负体积而停止计算；此外，网格随着边界运动实时更新，网格数量随着边界移动距离增加而急剧增加，尤其是大位移计算，网格总数增加导致计算效率降低，甚至无法继续计算[12].这两方面是动网格发展的瓶颈，使动网格在包含高速旋转螺旋桨的类物理数值模拟方面落后于重叠网格.研究者开始探讨采用移动子区域代替移动边界法，解决动网格法近场网格畸变问题[13-15].本文作者在已实现AUV自航运动的类物理数值模拟的基础上[15-16]，将采用移动子区域结合动态层方法对AUV给定纵倾角变化和航速变化，而螺旋桨以恒定转速旋转的AUV自航下潜(以下简称强制自航[17])操纵运动进行类物理数值模拟.

1 数值方法

1.1 运动描述

建立满足右手系法则的大地坐标系E-ξηζ和载体坐标系G-xyz，如图1所示.大地系下Eζ垂直指向地心.载体坐标系原点与载体重心G重合，Gx沿AUV主对称轴方向，向首为正.对应大地系和载体系下的速度分量分别为v1,v2,v3和u,v,w.AUV通过调整纵倾实现下潜运动(见图1)，分为3阶段.第1阶段，AUV通过打舵，使载体具有纵倾角速度，调整载体的纵倾角，准备下潜；第2阶段，载体在给定纵倾角下，以及螺旋桨推力作用下进行定向直航下潜运动；第3阶段，载体到达一定深度，回调纵倾角进入定深直航.

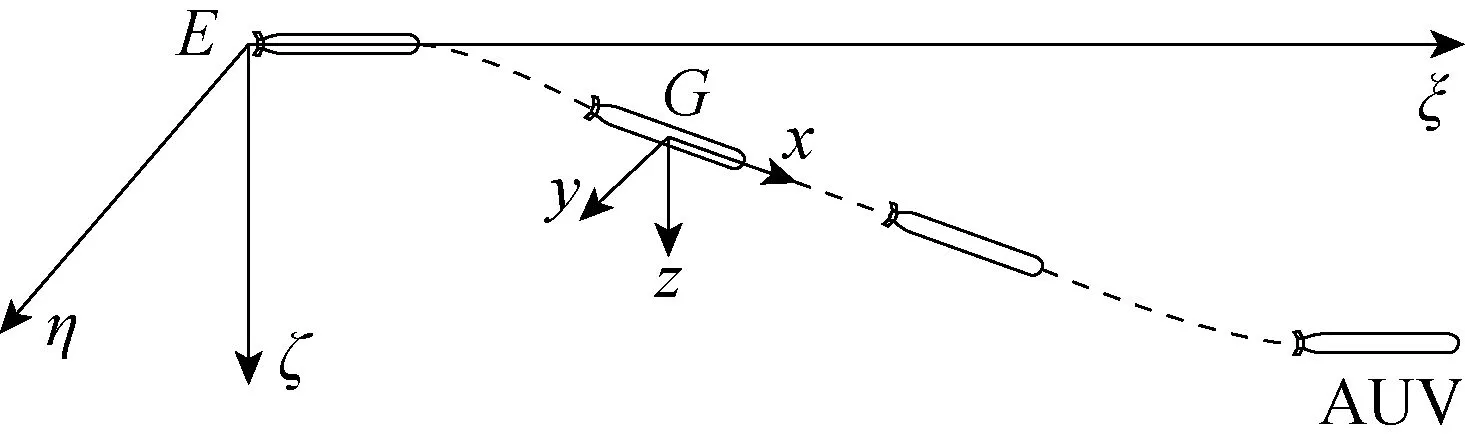
图1 AUV自航下潜示意图Fig.1 AUV diving scheme by self-propulsion

本文将这3个阶段AUV的运动提取出来，预定义AUV纵倾，水平和垂向速度变化，以及螺旋桨旋转运动，模拟AUV强制自航下潜运动.其中AUV的纵倾角变化，以纵倾角速度(ω2)给出，如图2所示，在第1阶段和第3阶段，载体有纵倾角速度变化，第2阶段为恒定纵倾角下潜，则纵倾角速度为0.

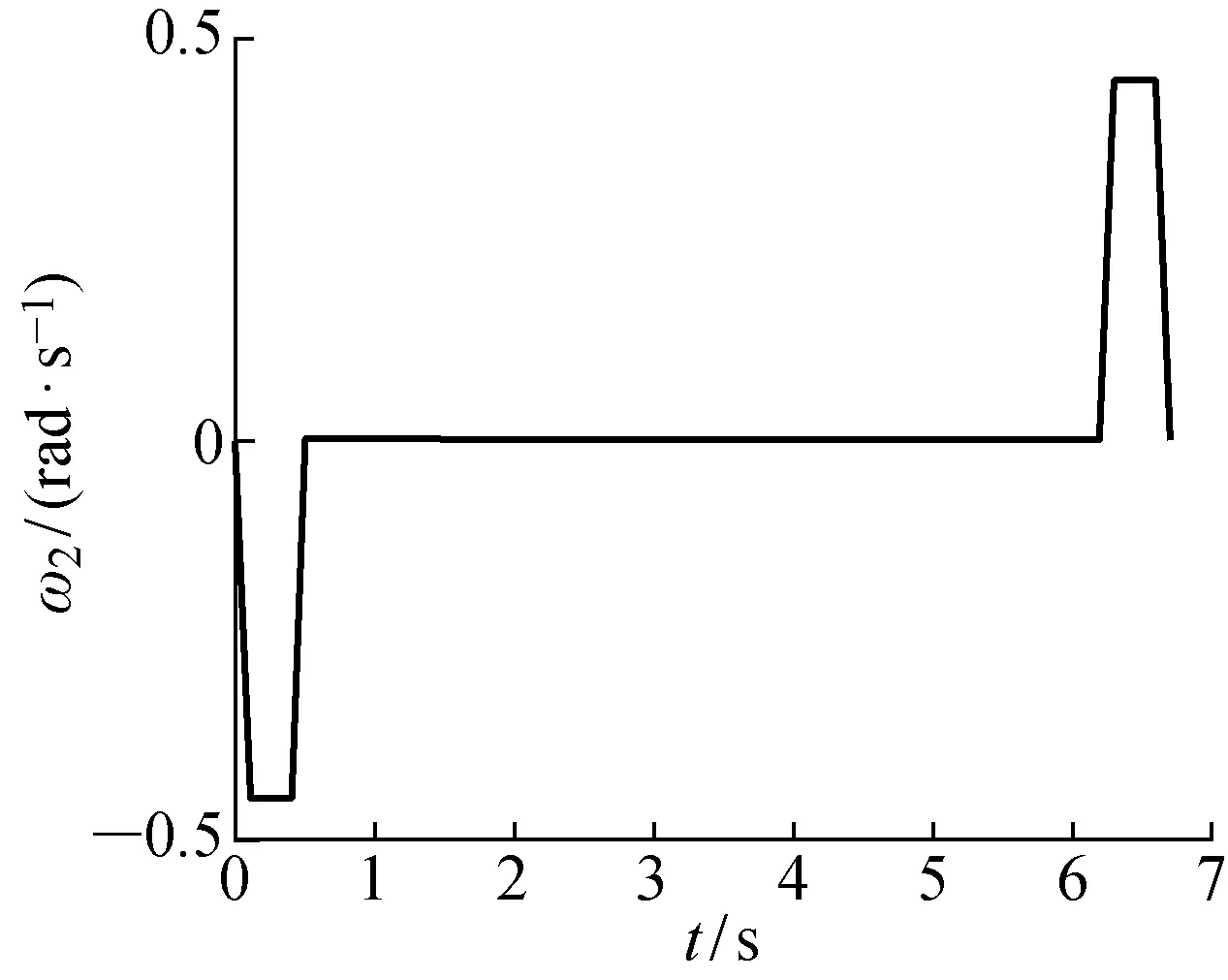
图2 AUV下潜运动角速度变化Fig.2 Pitch rate during AUV diving

1.2 动网格分区和网格模型

数值模拟的整个流域分区如图3所示.流域为方形流域，共为9个分区.此方形域的中间包括核心区域C，AUV左侧小流域为L，AUV右侧小流域为R.此方形域的外围包括：上方域S1，下方域S2；左方域S3，右方域S4；前方域S5和后方域S6.网格模型为多块混合网格，各部分的网格类型和运动形式如表1所示.C区域包括AUV载体、舵翼和螺旋桨，以及对应的扰动区域.此区域中，螺旋桨区域和尾迹区域采用非结构网格离散.AUV和舵翼为结构网格.除此外，C流域内的体网格为非结构网格，适用于AUV纵倾运动导致的网格变形和重构.其他外围区域S1～S6为结构网格.当螺旋桨旋转运动时，螺旋桨流域随着螺旋桨旋转.AUV拖曳着螺旋桨和舵翼在C流域内作纵倾旋转运动.当AUV有纵向运动和垂向运动时，C、L和R随AUV作纵向和垂向运动.S1和S2作垂向运动.外流域中运动流域的网格采用动态层方法进行更新.图4给出载体自航下潜的网格图，包括AUV在垂直对称面上的网格图和尾部局部放大图.

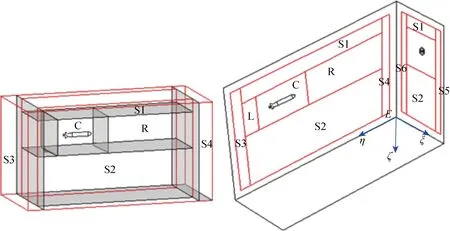
图3 AUV 下潜运动流场拓扑结构Fig.3 Domain topology of AUV diving

表1 网格类型和运动形式Tab.1 Mesh type and motion pattern

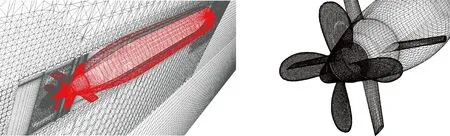
图4 AUV 网格系统Fig.4 AUV grid system

1.3 用户自定义函数(UDF)

AUV强制自航下潜运动通过编写UDF实现，如图5所示的流程图.其中n1,n2和n3表示螺旋桨转速绕Eξ,Eη,Eζ3轴的角速度分量；R1和R3为AUV在Gx,Gz的阻力分量；T1，T3为螺旋桨沿Gx,Gz的推力分量.此流程图包含3个模块：螺旋桨模块、AUV模块和流域模块.在螺旋桨模块中，根据AUV纵倾角，计算螺旋桨旋转速度分量，计算螺旋桨推力，并将此推力传递给AUV；在AUV模块，计算AUV速度在大地下的分量，并让AUV以纵倾角速度ω2和线速度v1,v3运动，求解流体力学方程，获得局部坐标下的速度分量，并将速度分量进行坐标转换；在流域模块中，局部模块随着AUV作纵向和垂向平移运动，远场水平流域也做纵向和垂向运动，远场垂直流域作垂向运动，各界面采用非一致连接实现界面的变量传递.

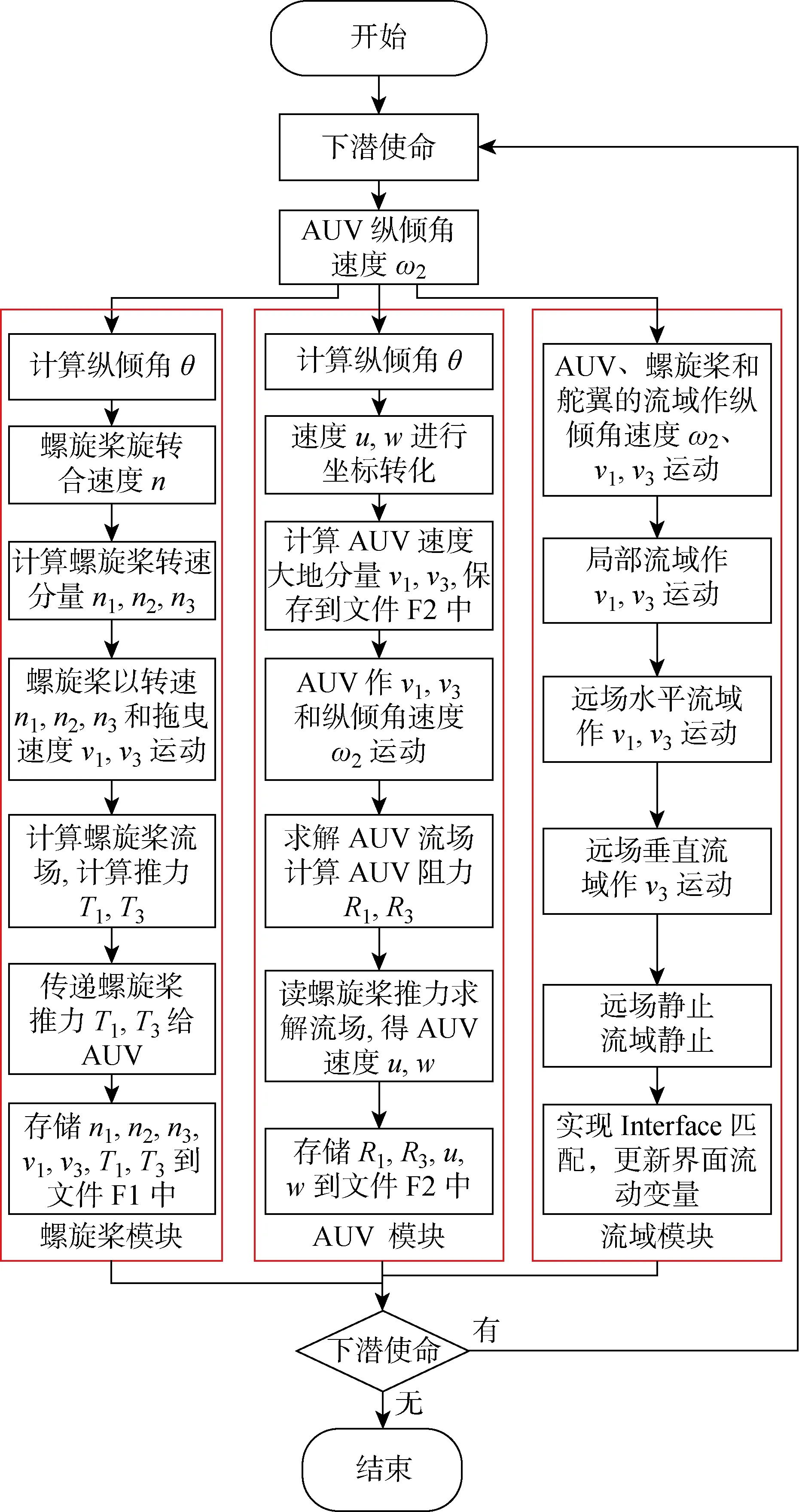
图5 AUV强制自航下潜运动流程图Fig.5 Flowchart of AUV forced diving motion

2 数值验证

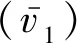
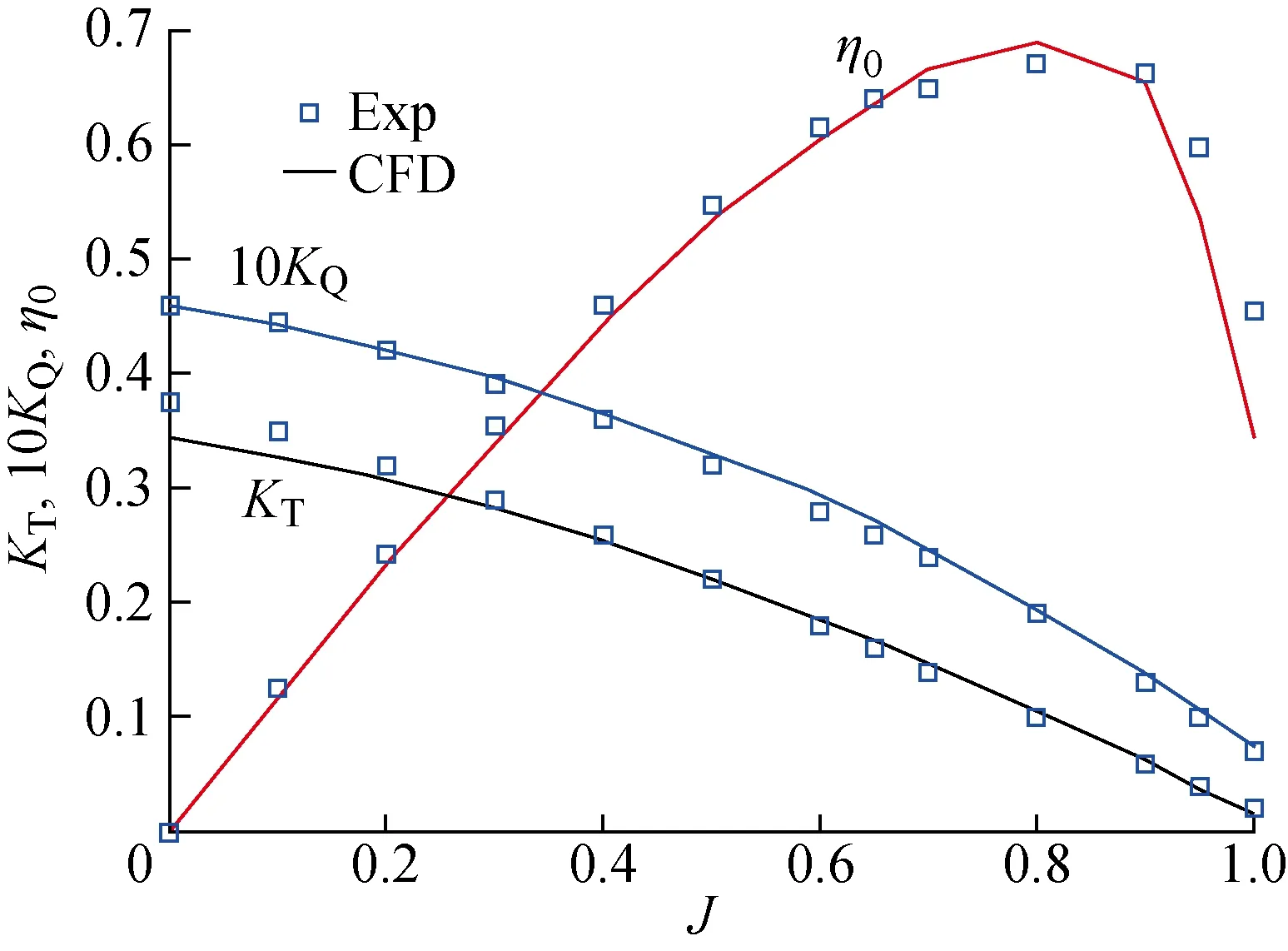
图6 敞水试验的试验结果与数值结果对比Fig.6 Comparison of experimental and numerical results of open water curve

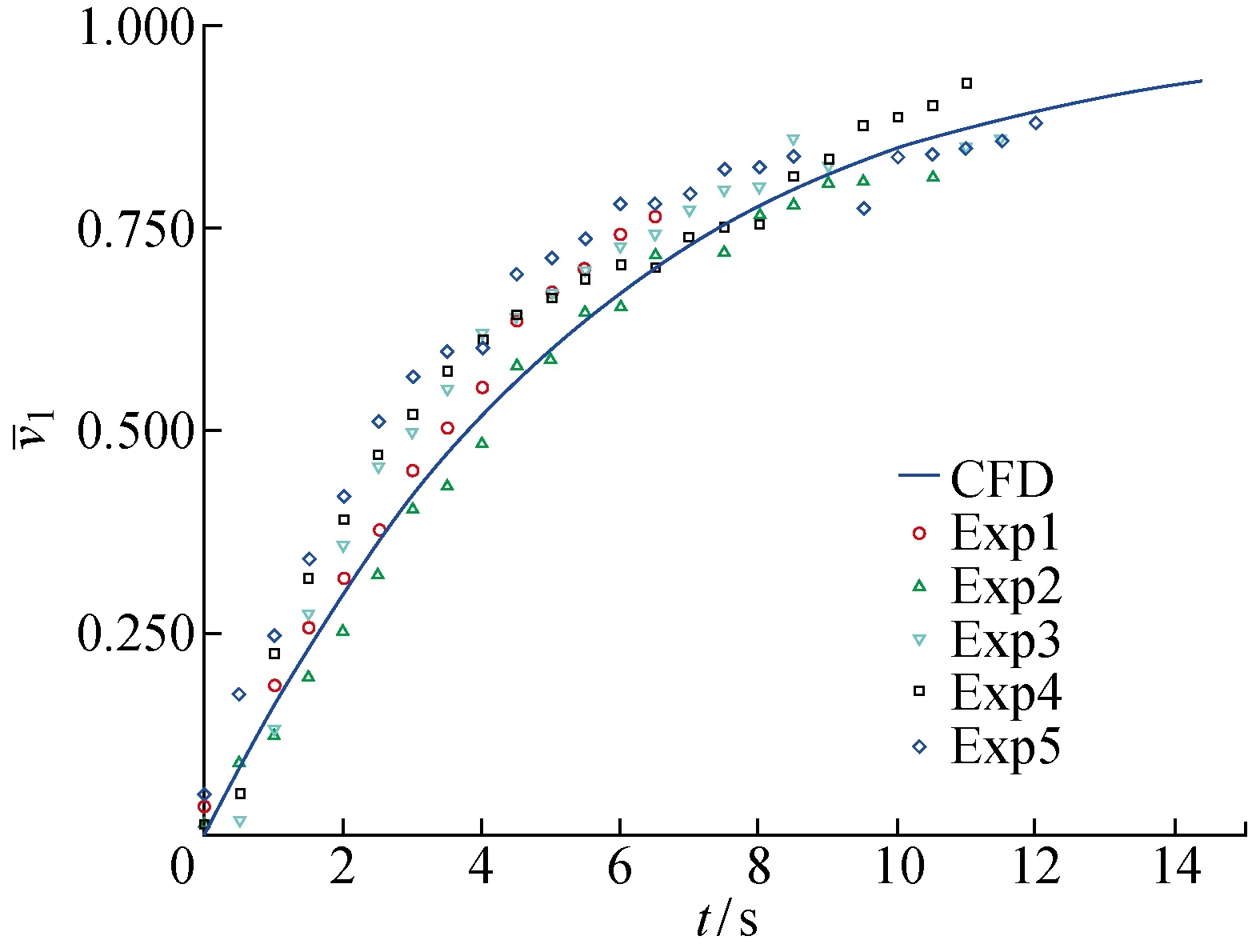
图7 AUV自航试验速度对比Fig.7 Comparison of computational and experimental data of AUV’s velocity in self-propulsion

3 数值结果

数值模拟AUV自航下潜过程，AUV以一定的速度和角速度开始下潜运动.初始速度为接近0的一个非常小的数，待定常计算收敛后，开始以此为初始值，AUV调整纵倾下潜.计算时间步长为螺旋桨旋转1° 所对应的时间，垂向航行距离约1个载体长度，纵向航行距离约5个载体长度，对应的物理时间接近7 s.图8给出4个典型时刻(t=0.1,3.0,6.0，6.7 s) AUV下潜过程中垂直面对应的网格图.载体在垂直下潜过程中有明显的纵倾变化，同时具有纵向和垂向运动.在这过程中，网格质量仍然保持较好.

图8 不同时刻网格图(η=0平面)Fig.8 Meshing at different times (plane of η=0)

整个下潜过程AUV受力和螺旋桨推力分别如图9和10所示.由图9可见，AUV调整纵倾，从静止开始快速加速到最大速度，则AUV在Eξ和Eζ具有较大加速度，对应的阻力R1,R3都较大.尤其是垂向阻力，在载体快速改变纵倾时，对应的垂向阻尼变化显著且振荡.这在载体改变纵倾回航阶段也体现明显.这主要是由于载体纵倾角速度过大引起的.当载体处于恒定纵倾角定向下潜时，阻尼趋于稳定.推力方面，载体在强制下潜和回航调整纵倾时，对螺旋桨推力影响较大，纵向推力和垂向推力都变化显著.载体无纵倾变化时，推力也趋于恒定值.因此，对于自航直航或自航下潜运动，航速应该由静止开始慢慢增加，否则载体加速度太大，流场扰动影响较大，趋于稳定的时间增加，则不仅需要更大的力达到对应的航速，流场也需要更长的预行段长度才能趋于稳定.

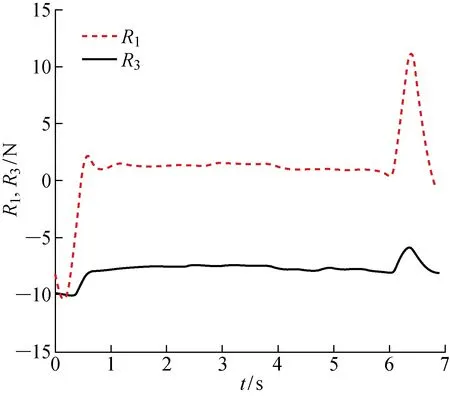
图9 AUV 在纵向和垂向的阻力Fig.9 AUV resistances along longitudinal and vertical directions

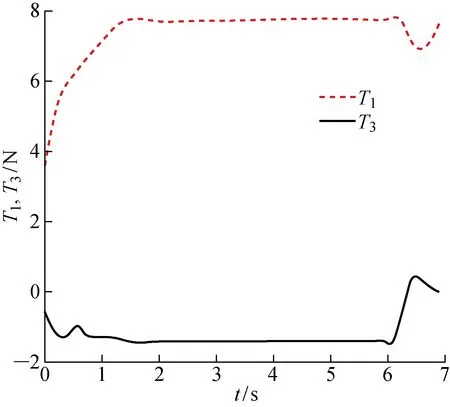
图10 螺旋桨在纵向和垂向的推力Fig.10 Propeller thrusts along longitudinal and vertical directions

图11为AUV下潜不同时刻的AUV尾迹(v1)云图(注：远场速度为0).由图可见，载体纵倾变化，将导致AUV拖曳的螺旋桨尾迹发生变化.当AUV绕着载体重心出现埋首下潜时，AUV尾部则绕重心往上运动，由图11(a)可见螺旋桨尾迹往上扭曲，呈现上甩现象；当载体无纵倾变化时(t=0.5,3.2,6.1 s)，螺旋桨尾迹沿着载体纵轴方向；当载体达到一定深度，回调纵倾到直航时，载体抬首，对应的载体尾部则向下运动，螺旋桨尾迹中可见明显的下摆现象.此外，螺旋桨尾迹中可见螺旋桨旋转运动有明显的梢涡泄出，以及与梢涡运动方向相反的毂涡.

图11 不同时刻AUV尾部速度放大图Fig.11 Closed-up velocity contours at AUV’s stern at different times

4 结论

海洋载体或空中飞行器的类物理数值模拟研究是数值模拟研究的最终目标，这种方法可以用数值模拟完全代替复杂、昂贵、风险性极高、周期长的试验，有利于以较小的成本设计出性能更优的载体，预报出已设计载体复杂操纵运动的各种动态特性.随着计算流体力学的发展和超级计算机计算能力的提高，这种类物理数值模拟变得可能，已经可以对一些载体的操纵运动进行类物理数值模拟.实现这种类物理数值模拟的关键技术是预报的精度和计算效率.可以采用超级计算机提高计算效率，但是网格技术仍然是这种数值模拟的关键点.

本文基于多块动态混合网格及动态层区域法实现了AUV垂直面内自航下潜操纵运动的类物理数值模拟.相对于非结构动网格方法和动态重叠网格法(前者需要20～30 d的时间[16]；后者进行自航数值模拟在高性能机上通过减少质量进行加速计算，仍需1～2个月[7]，且只能给出定常运动结果)而言，该方法计算速度快，精度高.数值模拟不需要减小质量，能获得载体自航下潜运动全程的计算结果，使数值计算在普通台式机(i5-6400 CPU @2.70 GHz，2.70 GHz，内存16.0 GB)上以4个处理器并行计算，历时12 d左右完成.本文为水下载体或空中飞行器的复杂多自由度耦合的操纵运动的类物理数值模拟提供了方法.未来将类物理数值模拟扩展到更多自由度耦合，更加复杂的海洋环境下的载体操纵运动预报中.