基于差和共阵的新型高自由度互质阵
2021-04-06陈禹蒲马晓川
陈禹蒲 马晓川 李 璇
(中国科学院声学研究所水下航行器信息技术重点实验室 北京 100190)
(中国科学院大学 北京 100049)
1 引言
波达方向(Direction Of Arrival, DOA)估计作为阵列信号处理的一大热点问题,在雷达、通信和声呐等研究领域都有着广泛应用[1–3],而阵列自由度(Degree Of Freedom, DOF)限制了一个阵列DOA估计时所能分辨的最大信号个数。对于一个长度为 N的均匀线列阵(Uniform Linear Array,ULA)其自由度往往受限于阵元个数,因此能否获得比阵元个数更多的自由度成为学者的研究焦点。人们发现,从共阵的角度对稀疏阵进行处理,可以获得远大于阵元个数的自由度[4–6],并在共阵的基础上给出了合理的处理方法[7],后文称为共阵MUSIC算法,使用该算法时,共阵中最长的ULA段直接决定了稀疏阵的最大自由度。最小冗余阵(Minimum Redundancy Array, MRA)作为稀疏阵的一大代表,在要求共阵全为ULA的条件下对阵列结构进行优化[5],具有最大的无孔洞共阵。最小孔洞阵(Minimum Hole Array, MHA)则把最小化孔洞数目当作优化目标,同时要求共阵的权重系数为1[8]。MRA和MHA都能在 N 个阵元下获得O (N2)的自由度,使得自由度较相同阵元数下的ULA有大幅度提高。然而,它们都没有阵元位置的闭式解,且大阵元下的阵元位置求解复杂度高。因此嵌套阵(Nested Array, NA)应运而生,它由两个子阵形成嵌套结构[9],同样能在 N 个阵元下获得O (N2)的自由度,并且阵元位置清晰明了,易于计算。但嵌套阵有一个半波长间距的子阵,该子阵较密的阵元排布导致嵌套阵的互耦效应较其他稀疏阵更强,会影响DOA的估计效果[10–12]。
互质阵(Coprime Array, CA)既有闭式解,其互耦效应也优于嵌套阵,它由两个阵元数分别为M和 N 的子阵构成, M与 N互质,子阵阵元间距分别为 Nd和M d ,可以获得的自由度为O (MN)[13],其中d 为半波长间距。借助互质阵进行DOA估计的算法有很多,如共阵MUSIC类算法[7,14]和压缩感知类算法[15,16],但估计类算法都无法弥补互质阵的共阵中存在孔洞的问题,相较NA,共阵中的连续线阵不够长,使得它的自由度逊色于嵌套阵,因此学者在提高互质阵共阵中的ULA段长度方面进行了大量研究。最为简单的方法是将一个子阵的阵元个数改为 2M ,其余条件不变,使得共阵在− MN到MN内均是连续的[7],为了方便区分,将这种阵型称为扩展互质阵,同时将原始的互质阵称为原型互质阵。在此之上,又出现了广义互质阵,广义互质阵包括两种阵型结构,一种是CACIS(Coprime Array with Compressed Inter-element Spacing),一种是CADiS(Coprime Array with Displaced Subarrays)[17], CACIS压缩了某一子阵的阵元间距,且压缩因子越大,共阵ULA越长,前述的扩展互质阵仅是CACIS的一个特例,CADiS则是将互质阵的某一子阵移至距另一子阵一定距离的位置。放置多级级联子阵的稀疏阵也尝试构建新的阵列结构,它将多个相同的稀疏阵级联在一起,并给出了各子阵间的放置距离,稀疏子阵的自由度越高,获得的级联阵自由度就越高[18]。精简互质阵(Thinned Coprime Array, TCA)讨论了扩展互质阵的共阵冗余,提出即使删掉M/2」个阵元,扩展互质阵的性质依旧不会改变[19],也就意味着同等阵元总数下,TCA的自由度会高于扩展互质阵。还有一种借助矩阵填充理论,通过重构Toeplitz协方差矩阵来使共阵ULA变长的方法[20]。
前面所提的方法都是基于差分共阵来提高互质阵的自由度,那么和共阵对于原型互质阵自由度的提高是否有帮助?针对这一问题已有文献进行了解答,文中借助矢量化由时域与空域信息共同构成的共轭增广协方差矩阵(Vectorize Conjugate Augmented MUSIC, VCAM),在虚拟域构建了差分阵与和共阵共存的差和共阵[21],和共阵不但能填补差分阵的部分孔洞,还能提供一段额外的ULA,致使原型互质阵在差和共阵下拥有远超于仅使用差分阵的自由度。但是仔细观察原型互质阵和共阵与差共阵的阵元位置,可以发现两者的阵元除了互补关系外,还存在重叠关系,即有不少的和共阵阵元与差共阵阵元重叠,从而导致阵元冗余,无形中丢失了一部分的自由度。
为了最大限度上利用和共阵所提供的阵元,希望和共阵能够在填补差共阵孔洞的同时产生与差共阵之间尽量少甚至没有的阵元重叠。借此,本文提出了一种新的阵型,在广义互质阵CACIS的基础上添加一个位于原点处的单阵元,并将CACIS整体放置在与该单阵元相隔一定距离的位置,文中将这种阵型命名为放置互质阵(Displaced Coprime Array,DCA)。通过一定的放置距离,让阵型的和共阵与差共阵相互错开,使它们正好互补,又没有多余的阵元重叠,最大限度上利用了和共阵带来的自由度。之所以选用CACIS结构,是因为它相较普通互质阵连续阵元更加集中,在两者错开一定距离后,更便于和共阵与差共阵之间的性质互补。文中给出了DCA的放置距离以及阵元位置的闭式表达,并对和共阵与差共阵的连续阵元和孔洞位置以及两者之间的关系进行了理论推导。此外,还给出了DCA所能提供的最大自由度的理论表达式,并借助仿真实验验证了放置互质阵的有效性。
2 放置互质阵

以半波长为基本单位描述阵元位置,子阵1和子阵2的阵元位置S1和S2分别表示为
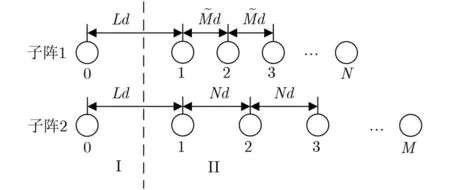
图1 放置互质阵



3 VCAM算法

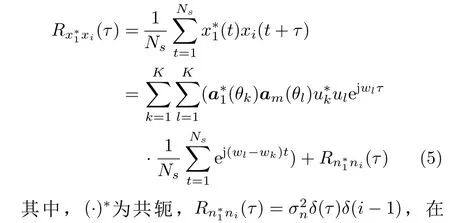


4 放置互质阵的差和共阵特性
4.1 差和共阵的定义
差和共阵包含差共阵与和共阵,它们的阵元位置分别由差集与和集给出,这两个集合都是由阵列各阵元相互加减得来的,根据相加减的阵元所属子阵不同,将差集与和集进一步分为互差集、自差集、互和集与自和集,具体定义如下所述, m和n 取值范围均为0 ≤m ≤M −1,0 ≤n ≤N −1。


4.2 差和共阵的性质
要想得知差和共阵的性质,有必要先讨论差集与和集的性质,放置互质阵的差集 Ld与广义互质阵CACIS的差集定义一样,除了满足文献[17]中证明过的几个性质外,差集还满足命题1中的性质。
命题1 互差集 Lcd在范围[MN −(N −1),MN −N]内的孔洞为


3个命题的证明略。图2给出了( M,N)=(6,5),压缩因子p =2时 DCA的4个重要集合与共阵 D的结构,黑点代表阵元,× 代表孔洞。从图中可以看到,自和集能够延长和集整体的连续段范围,且互差集与互和集间存在互补关系,通过让CACIS整体与原点阵元相隔 L,和集整体后移了 2L,在这里2L=18,这一放置操作既让互差集与互和集的孔洞互补,也避免了两者连续段的重叠而导致的自由度损失,能够最大限度上利用和集带来的自由度增益,最终得到的差和共阵D如图2(e)所示。
4.3 自由度分析
根据命题3性质(2)给出的范围,由于2 −N ≤0,因此当=1时,差和共阵D能得到最长的连续整数段为[ −(2MN −N +1),2MN −N +1],此时DCA能获得最大自由度,取值为2 MN −N +1。以往稀疏阵的算法中较多的都是借助矢量化数据协方差矩阵得到差分共阵来进行DOA处理,所以它们所提供的自由度不会超过物理孔径[24],但差和共阵的使用能够突破这个限制,因此使用差和共阵的阵列所得到的自由度会远大于仅仅使用差分共阵得到的自由度,下面对使用差和共阵的两种阵型,DCA与原型互质阵[21]进行自由度的比较,将后者记为CA(VCAM)。在相同阵元数 P下,两者子阵阵元数的最优选择以及所能获得的最大自由度如表1所示,为使两者都能获得最大的自由度,默认DCA的=1, CA(VCAM)的M >2。
在满足 M与N 互质的条件下,借助算术平均几何平均不等式(Arithmetic Mean-Geometric Mean(AM-GM) inequality)[25],根据两阵型DOF的表达式可以得到不同阵元总数 P下的阵列最优配置。互质阵的子阵阵元数至少为2个,要想DCA存在,则P ≥7 ,对表1中DCA和CA(VCAM)以 P为表达式的自由度进行比较,根据 P的取值情况,通过简单的作差计算不难得出结论:DCA的自由度不小于CA(VCAM)且当 P 为P ≥12 的偶数或 P 为P ≥9的奇 数时,DCA能获得比CA(VCAM)更高的自由度。
5 仿真验证
前文从理论分析证明中给出了DCA的诸多性质,这一节将讨论包括NA, CACIS, CADiS, CA(VCAM)和DCA在内的几种阵型的性能,为保证各阵型都能获得最大的自由度,涉及压缩子阵间距的阵型都令压缩后的子阵间距为1,CADiS两子阵间的距离为 LDiS=N +1,D C A 的放置距离为LDCA=(MN −N +1)/2,子阵阵元数的选取均以最大化自由度为目标。

图2 放置互质阵(M,N,p)=(6,5,2)

表1 两种阵型的最优设计及最大自由度
5.1 自由度比较
以总阵元数 P 为变量,给出了 P从7到99变化时,5种阵型的自由度变化曲线如图3所示。随阵元总数的增大,各阵型的自由度都越来越高,且放置互质阵DCA相较其他几种阵型自由度上升速度更快, P越大,DCA的自由度与其他阵型相隔越大,从图中可以看出,使用差和共阵的两种阵型CA(VCAM)和DCA的自由度始终大于其他几种阵型,由于DCA较CA(VCAM)更加合理地利用了和共阵的阵元位置,避免了和共阵与差共阵的阵元冗余,其在所获得的自由度上更占优势,同时DCA通过一定的放置距离拥有了近似于CACIS两倍的自由度。上文给出的有关DCA自由度比较的结论在图中也得到了验证。
5.2 同阵元数下的蒙特卡罗实验
下面通过蒙特卡罗实验对几种阵型在不同条件变化下DOA估计的均方根误差(Root Mean Square Error,RMSE)进行对比,假设蒙特卡罗试验次数为 I 次,则 K个信号入射时,阵列DOA估计得到的RMSE定义为
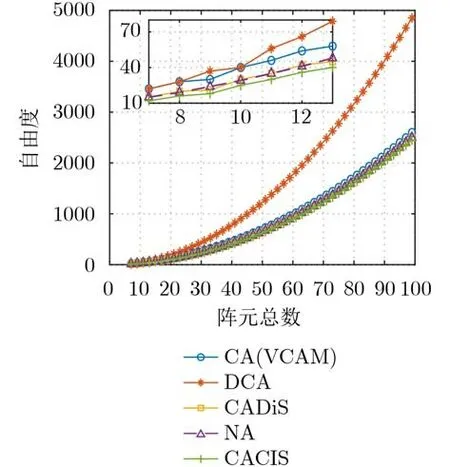
图3 各阵型自由度随阵元总数的变化

5.3 同孔径下的蒙特卡罗实验
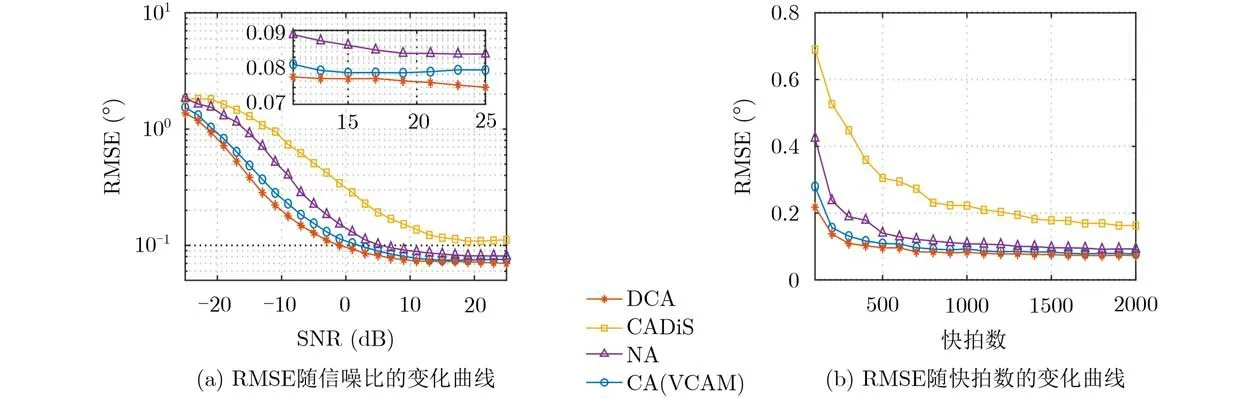
图4 同阵元数下各阵型的RMSE变化曲线
在相同阵元数的条件下,各阵型由于阵元排布方式不同具有不同的阵列孔径,下面观察阵列孔径相同时,各阵型DOA估计的均方根误差,同样进行500次独立实验,对5种阵型进行RMSE的比对,各阵型在同孔径下的阵型配置如表2所示,孔径以d为单位,其中DCA用最少的阵元个数获得了最高的自由度。
假设有43个远场信号从[ −60o,60o]入射,其他条件不变,RMSE在–30 dB到20 dB内随信噪比的变化曲线如图5(a)所示。固定信噪比为–20 dB,RMSE随快拍数的变化曲线如图5(b)所示。从图5中不难看出同孔径条件下,各阵型的估计误差不会完全一致,这也许是因为共阵MUSIC算法是基于共阵ULA段进行处理的,使用差分共阵的CACIS,CADiS和NA,它们的最长共阵ULA段孔径受限于物理孔径,因此在同孔径条件下的实验中,三者的RMSE近似相等,而DCA在两种变化情况下均展现出了其优越的估计性能。由此可见,对于使用了差和共阵的阵型,物理孔径对其估计性能的影响不起决定性作用。
6 结论
本文提出了一种名为放置互质阵的新型互质阵,并在差和共阵的基础上进行DOA估计,阵型把CACIS与原点处单阵元分开放置一定距离,这样能够让差共阵与和共阵的阵元位置恰好互补,避免差共阵与和共阵的阵元重叠,充分利用和共阵所提供的自由度,使得在相同的阵元数下,DCA所能获得的最大自由度近似是CACIS最大自由度的2倍。为了更好地认知DCA的共阵构成,文中分析讨论了DCA差共阵与和共阵的连续阵元及孔洞位置,结合两者关系给出了DCA所能获得自由度的闭式表达,最后的理论分析和仿真实验表明了DCA的高自由度特性及优越的DOA估计特性。

表2 各阵型同孔径下的阵型配置
附录1 命题1的证明
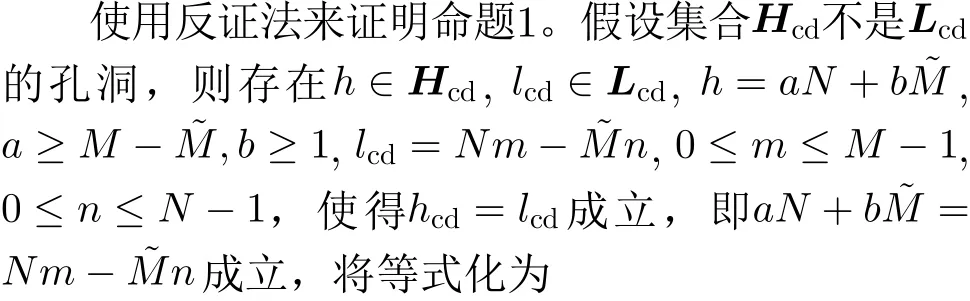
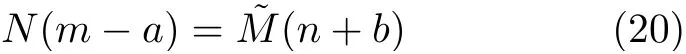

附录2 命题2的证明
(1) 设整数lcs∈Lcs, lcs满足


图5 同孔径下各阵型的RMSE变化曲线



