基于射线声学的水下传感网络静默定位算法
2021-04-06李浩铭鄢社锋徐立军
李浩铭 鄢社锋* 徐立军 季 飞
①(中国科学院声学研究所 北京 100190)
②(中国科学院大学 北京 100049)
③(华南理工大学 广州 510641)
1 引言
随着海洋探索需求增强,水下传感网络技术正在得到越来越多的关注,而为水下传感节点提供定位与导航服务正是水下传感网络的主要任务之一[1]。对于水下传感网络定位技术,近年来国内外学者的关注点主要集中在各节点间是否需要时钟同步[2]、是否考虑声速分布不均匀因素[3–6]、定位协议[7–9]以及定位算法的附加功能[3,4,10,11]等方面。文献[2]提出了一种各节点时钟同步情况下基于双程时间测量的水声定位算法,该算法在常声速梯度假设下,采用高斯-牛顿法对目标位置进行估计。文献[3]提出了联合解决水下传感网络中定位和时钟同步的算法,待定位节点与信标节点间采用应答方式获取双程传播时延,并引入一个积分常数来修正声速分层的影响。文献[4]提出了基于双程时延测量的位置和时钟联合估计方法,采用等效常梯度声速剖面来解决声速分布不均带来的定位误差,但定位过程较复杂,周期较长。文献[5]提出了各节点间时钟已同步条件下考虑声线弯曲的水下传感网络定位算法,通过卡尔曼滤波优化接收到的时延信息,再采用凸优化方法对待定位节点位置进行估计。文献[6]提出了基于双程时延测量并结合声线跟踪的定位算法,采用高斯-牛顿法估计最优的待定位节点位置,但在信标节点布阵不佳时,算法发散。文献[7]提出了基于移动预测的水下传感网络定位算法(Scalable Localization scheme with Mobility Prediction, SLMP),待定位节点根据自身的运动模型对自身位置进行预测,并通过信标节点的信息进行位置和运动模型的更新。文献[8,9]提出了通过单信标测距对水下潜器进行定位的方法,潜器通过自身配备的惯性导航设备获取自身轨迹,再结合行进时获取的与信标间到达时间(Time Of Arrival, TOA)或到达角(Angle Of Arrival,AOA)信息,采用虚拟长基线方法估计出自身绝对位置。文献[10]提出了通过最小二乘联合估计所有节点的时钟信息和待定位节点与各信标节点间距离,进而获取待定位节点位置的算法。文献[11]提出了一种分布式逐级网络节点定位的方法,通过对已定位节点的定位误差进行评估以将其升级为新的信标节点,从而扩大定位范围。
上述方法考虑了水下传感网络定位中的大部分情形,但均需要待定位节点反复与信标节点通信。在需要对多个待定位节点同时进行定位服务,或待定位节点因任务需求需要静默的情况下,上述方法均不适用。针对这些情况,文献[12]首次提出静默定位(Underwater Positioning Scheme, UPS)算法,该算法不需节点间时钟同步且待定位节点可全程处于静默接收状态,但该算法未考虑声速不均匀分布问题,且算法通过降阶法对待定位节点位置进行求解,存在定位盲区的问题。文献[13]采用增加信标节点的方式解决UPS算法的定位盲区的问题,但增加信标节点无疑会大大提高算法的应用成本。文献[14]对UPS算法进行了复现,并通过实验加以验证。虽然后续的研究人员在静默定位方面做出了很大的努力,但并没有解决最初的问题,即声速分布不均匀对UPS算法的影响,且没有从本质上解决定位盲区的问题。尽管在无线传感网络定位领域,文献[15]已经解决了定位盲区的问题,然而对于水下传感网络,此方法所需的通信量和计算量依然很大,这也导致其无法直接在水下传感网络中使用。
本文针对现有UPS算法的不足,提出了一种新的静默式水下传感网络定位算法。通过声线跟踪技术,解决了声速不均匀分布的问题。采用高斯-牛顿法估计最优的待定位节点位置,解决了UPS算法存在定位盲区的问题。同时针对水下传感网络各参考节点布放时容易出现的定位阵型不佳问题,引入了改进的Tikhonov正则化方法,根据迭代效果反馈控制正则化参数,提高了算法的稳健性。最后通过仿真分析,讨论了各个步骤的必要性和各项误差对算法性能的影响,验证了算法的有效性。
2 算法原理

假设信标节点A为定位发起节点,该网络内信息传递的顺序为A-B-C-D。在检测到待定位节点T处于该区域内时,信标节点A周期性广播定位数据包,其中包括其当前的时钟、经纬度和深度等信息,待定位节点T于自身时钟时刻 ta接收到来自信标节点A的定位发起信号。后面的信标节点依次在接收到前一信标节点发出的信号的一段时间τi,i=b,c,d后,广播其自身的定位数据包和处理
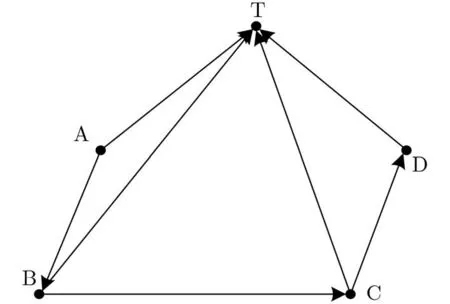
图1 水下传感网络静默定位流程



3 仿真分析
下面对所提算法进行仿真,并与相关算法进行对比。
3.1 定位区域及解的唯一性
设置4个信标节点的位置分别为(–2500, 2500,3000) m, (–2500, –2500, 2010) m, (2500, –2500,4000) m和(2500, 2500, 1050) m。为不失一般性,设置待定位节点实际位置坐标为(1000, 500, 100) m。设置按照Munk典型声速剖面设置水体声速,水深5000 m。在100 m深度平面上的目标函数‖G(X)‖2分布如图3(a)所示;在y =x −500的坐标平面上的目标函数分布如图3(b)所示。
由图3可见,理想布阵情况下目标函数在全空间内存在唯一最小值点,即为待定位节点真实位置,不存在多解情况。相比于UPS算法降阶方程组所带来的局限性导致其在信标节点附近存在定位盲区,且需要人工排除多解的情况,本文算法既可获得唯一解,又可在4信标通信范围内任意位置对待定位节点进行定位。
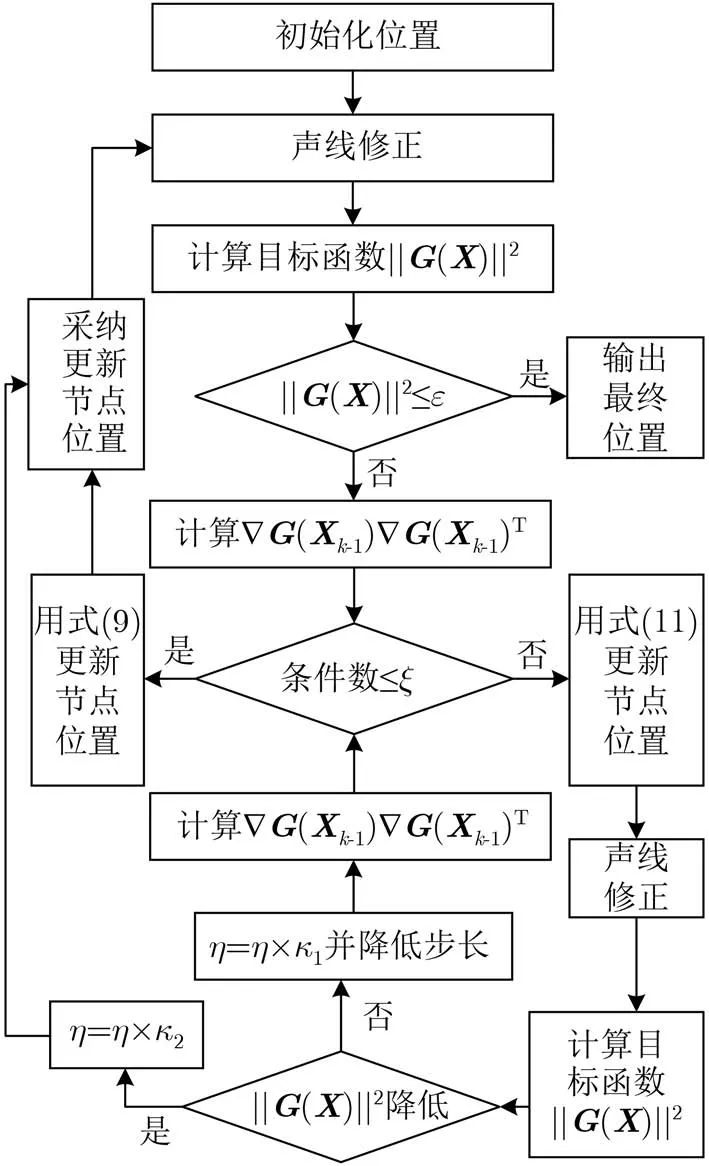
图2 基于射线声学的水下传感网络静默定位算法流程图
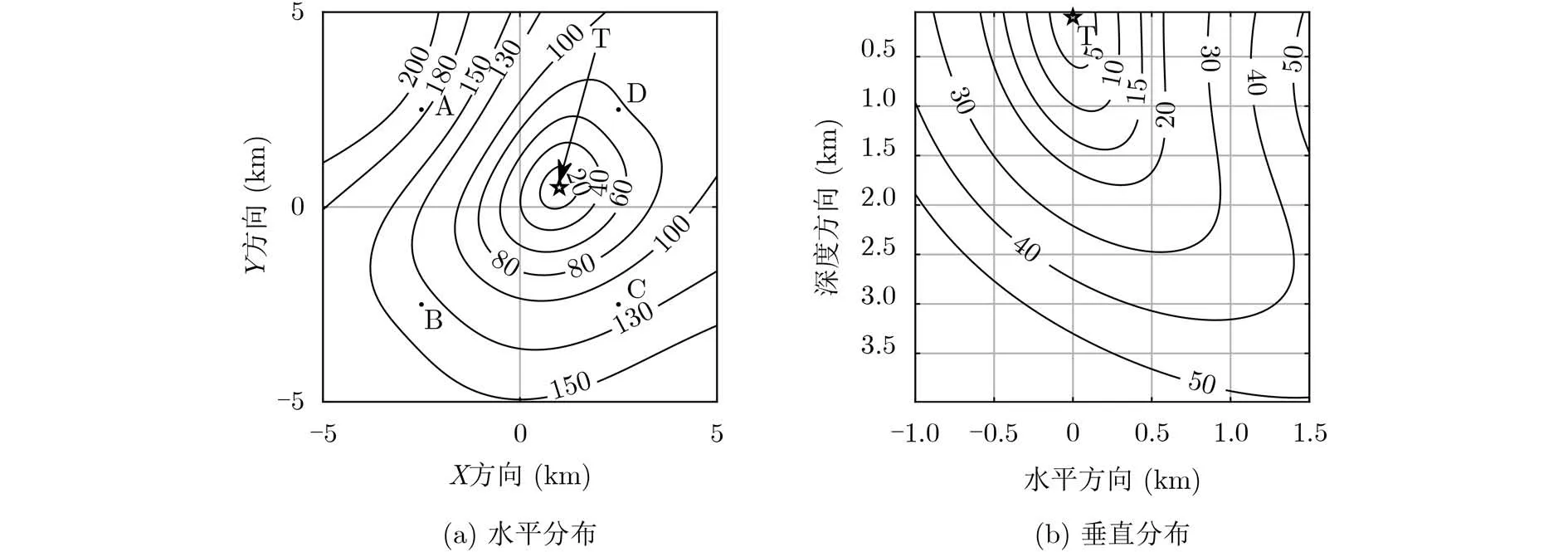
图3 布阵区域内目标函数分布情况
3.2 信标定位阵型不佳

3.3 误差分析
由本文第2节算法原理可以看出,本文算法定位精度的主要影响因素包括信标节点位置误差、测时误差和水下环境失配等。下面采用上述仿真条件,对算法涉及的各输入参数引入一定的高斯随机误差,并进行200次蒙特卡洛仿真,以分析各参数的误差对本文算法性能的影响,并与其他算法进行对比。
3.3.1 信标节点位置误差
对水下待定位节点定位前,需对各信标节点的位置进行标校,以得到信标节点的精确位置,包含水平位置和深度信息两方面。因此,信标节点位置误差对本文算法的影响,需要分信标节点的水平位置误差和深度误差两个方面进行讨论。
信标节点深度一般由配备的深度传感器测得,因此其深度误差来源于配备的深度传感器误差。本算法和UPS算法受信标节点深度误差影响如图5(a)所示。
水下信标节点的水平位置需要由测量船事先标校获得,一般地,测量船绕信标节点布放位置以圆形等对称航迹航行,期间多次对信标节点进行应答式测距,再结合测量船自身GPS信息,采用反转长基线原理等完成对信标节点水平位置的标校[17]。信标节点的水平位置误差来源于多方面,包括信标节点深度误差、测量船测时误差、声速误差等。本文算法和UPS算法受信标节点的水平位置误差影响如图5(b)所示。
可以看出,随着信标水平位置误差和深度误差的增大,本文算法的定位误差也随之增大。由于UPS算法定位误差远大于本文算法,相比之下,其对于信标的水平位置误差和深度误差均不十分敏感。
可见,信标节点位置的准确性将直接影响本文算法的定位精度。因此,在应用本文算法前,获取信标节点的锚定准确位置,并考虑信标节点在水下位置的随机摆动,对于提高本文算法的定位精度是十分必要的。
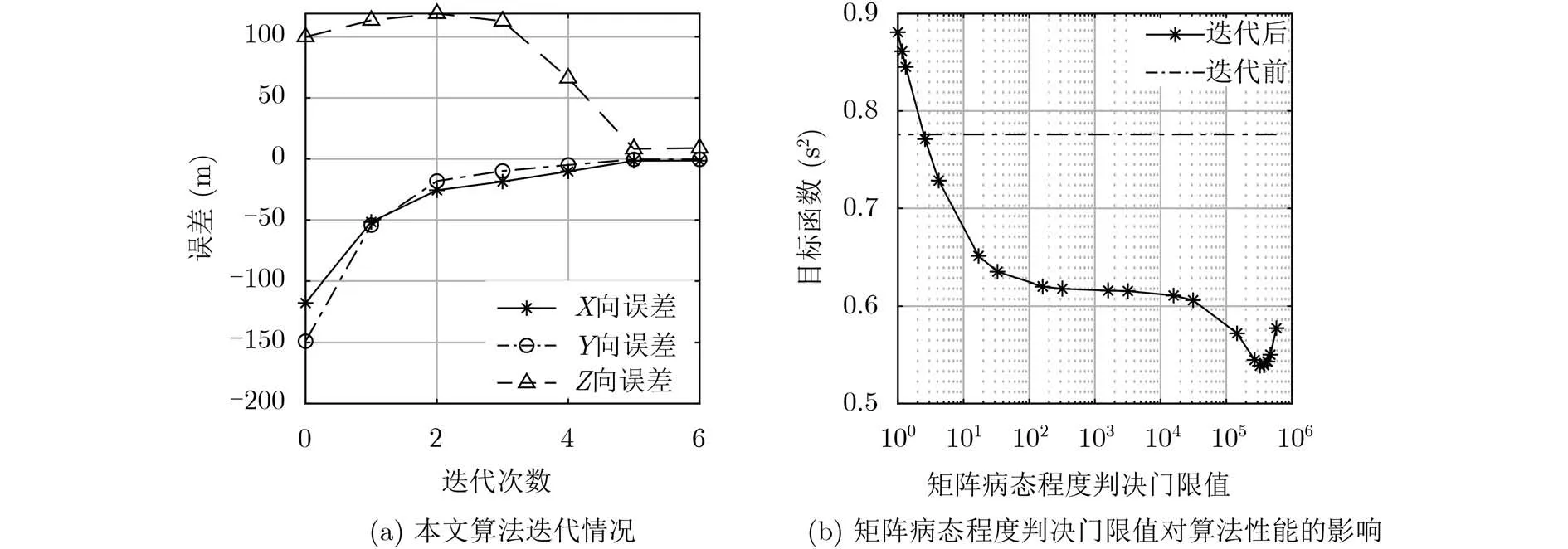
图4 定位阵型不佳时本文算法迭代情况
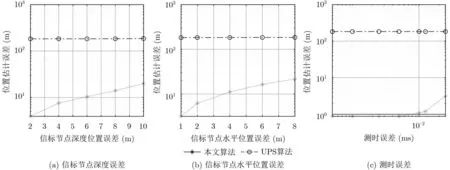
图5 各误差来源对定位结果影响
3.3.2 测时误差
本文算法属于基于时间测量的定位算法,信号到达时间的测量误差会直接影响算法的定位误差。
本文算法中,采用双曲调频(Hyperbolic Frequency Modulated, HFM)信号通过匹配滤波实现对信号到达时间的测量。匹配滤波器的时间估计精度为1 /B,其中B为信号的带宽,并且,各节点间的多普勒和水声信道的多途效应也会对到达时间测量精度造成一定的影响。信号到达时间测量误差对本文算法和UPS算法的影响如图5(c)所示。可以看出,随着测时误差增大,本文算法定位误差也随之 增大,但误差仍显著小于UPS算法。
3.3.3 水下环境参数失配
本文算法中声线跟踪部分依赖于相对准确的水下环境参数输入,考虑到水下传感网络的应用场景主要在深海中,水底地形较为平坦,因此声速剖面的误差成为影响本文算法精确度的主要因素。
声速剖面的误差分为与深度无关的测量误差和与深度相关的时变偏差。此处引入剖面等效误差概念来表征声速剖面的失配程度[19],令

对算法中使用的1000 m以上水深的声速剖面加入一定的测量误差和时变误差,其最终的定位误差随剖面等效误差的变化如图6所示。可见,本文算法对声速剖面误差较为敏感,后续研究将针对此问题进一步展开。
4 结论
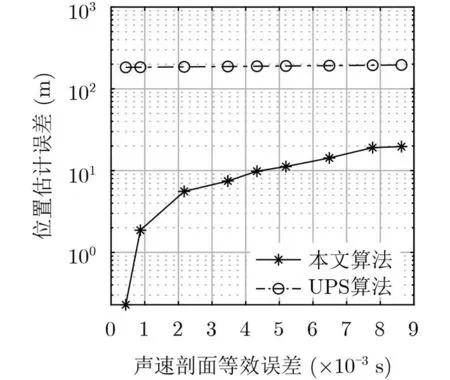
图6 定位误差随剖面等效误差变化关系
针对已有静默定位算法存在定位盲区、多解以及未考虑声速不均匀带来的影响等问题,本文提出了一种改进的静默式水下传感网络定位方法。算法通过融合声线跟踪技术和高斯-牛顿迭代方法使得算法可以在信标阵列通信范围内任意位置获得唯一的待定位节点最优位置,且修正了声速分层分布对定位结果带来的影响。同时,采用引入反馈控制机制的Tikhonov正则化方法,使得算法在信标阵型不佳的情况下,仍然保持较好的定位性能。仿真结果表明:该算法较已有的UPS算法具有更好的性能,且输入参数存在一定误差的情况下,仍能保持较好的定位效果,同时算法对信标布放阵型具有一定的稳健性。
