一种基于谱极化参数的双极化气象雷达杂波抑制方法
2021-04-06朱岱寅孟凡旺
汪 玲 田 凤* 朱岱寅 孟凡旺 吴 迪
①(南京航空航天大学雷达成像与微波光子技术教育部重点实验室 南京 210016)
②(中国航空工业集团公司雷华电子技术研究所 无锡 214063)
1 引言
气象雷达是一种具有高时空分辨率的降水探测系统,是大气观测必不可少的工具[1]。具有双极化功能的多普勒气象雷达[2]可以同时记录降水的微物理和动态特征,极大提高了定量降水估计(Quantitative Precipitation Estimation, QPE)[3,4]性能。一般情况下,QPE应用中使用雷达数据的前提是要有足够的测量精度,而雷达数据往往会受到杂波的影响。重要的是,与强降水相比,弱降水在杂波去除时可能很容易地被去除。因此,研究杂波抑制方法,在有效滤除杂波的同时保留气象信息一直是气象雷达信号处理的关键。
气象雷达杂波按多普勒速度不同主要分为静止地物杂波和运动杂波,相应地有针对各自特点的杂波抑制滤波器。高斯模型自适应处理(Gaussian Model Adaptive Processing, GMAP)[5]是一种典型的地杂波抑制技术,它可以解决气象目标和地杂波在时域重叠的问题。自适应杂波环境分析法(CLutter Environment ANalysis using Adaptive Processing, CLEAN-AP)[6]将杂波检测与滤波统一在一起。与GMAP相比,由于使用幅度和相位确定适当的凹口宽度[7],CLEAN-AP具有更好的杂波抑制性能。文献[8]利用双极化气象雷达在晴空模式下接收的地杂波数据训练模糊神经网络,自适应地计算地杂波各偏振参量隶属函数的参数,然后利用训练得到的地杂波隶属函数对降水模式下的地杂波进行抑制。但是,以上方法均不能去除运动杂波。
地面气象雷达探测遇到的运动杂波包括鸟类和昆虫的回波、海杂波和各种无线电频率干扰等。文献[9–12]详细分析了运动鸟类和昆虫的回波特征。文献[13]基于贝叶斯分类器,提出了一种海杂波识别方法。无线电频率干扰[14]在雷达平面位置指示器(Plan Position Indicator, PPI)呈现为点状、条带状干扰。由雷达系统本身引起的条带状杂波也会影响雷达数据的使用。大多数情况下,条带状杂波是PPI显示画面上沿某个方位向的连续距离门上的斑点,在频域观测时其多普勒速度不固定,传统的杂波抑制方法无法进行有效抑制。这些条带状杂波会影响雷达数据质量,降低雷达基产品及后续衍生产品的准确性。文献[15,16]介绍了条带状杂波在国际电信传输和雷达研究中心研制的毛毛雨雷达(IRCTR Drizzle RAdar, IDRA)中的影响,由荷兰Delft理工大学研制的MESEWI雷达系统[17]也存在这个问题。
为了能够同时有效去除静止地物杂波和运动杂波,并保留尽可能多的气象信息,本文提出了一种基于谱极化参数(Spectral Polarimetric Parameters,SPP)的杂波滤波方法。根据气象和杂波在距离-多普勒(Range Doppler, RD)域内的特征不同进行前者的保留和后者的抑制。首先利用气象目标的频谱极化特征和连续性构造谱极化参数并设置阈值,在RD域内生成一个2元掩模,其中“1”对应保留气象,“0”对应去除杂波。结合形态学方法,对2元掩模进行内部空洞填充和边界平滑,使被抑制的弱气象信息得到恢复。然后采用面向对象的思维,运用泛洪填充算法将2元掩模标记为气象对象掩模和杂波对象掩模。最后引入谱宽作为额外的参数,利用杂波对象谱宽普遍小于气象对象谱宽的特点,筛选出所有气象对象掩模并叠加在一起得到SPP滤波器。SPP滤波器适用于同时发射同时接收(Simultaneous Transmission and Simultaneous Reception, STSR)模式和交替发射同时接收(Alternate Transmission and Simultaneous Reception, ATSR)模式的双极化气象雷达,具有通用性。且本文算法是逐个对雷达径向数据进行处理的,具有较高的计算效率,可以实时实现。
本文各节内容安排如下:第2节首先引入双极化气象雷达谱极化参数,给出详细的定义;第3节详细阐述SPP滤波器的设计步骤;第4节讨论SPP滤波器的参数选择;第5节采用X波段和C波段双极化气象雷达实测数据对算法的性能进行验证;第6节给出结论。
2 谱极化参数
假设双极化气象雷达发射y 极化波、接收x 极化波,x ,y ∈{h,v}, 其中h 表示水平极化, v表示垂直极化。一次径向扫描得到的回波信号为 Sxy(r,t),其中 r 表示距离向,采样数为Nr, t表示驻留时间,采样数为 NDwell。对Sxy(r,t)回波序列进行1维离散傅里叶变换得到Sxy(r,v)个距离点的回波强度,而谱反射率因子s Zxy(r,v)还包含了气象目标的多普勒速度信息。

基于RD谱定义谱线性退极化比s LDR和谱相关系数s ρhv[18],如式(3)和式(4)所示
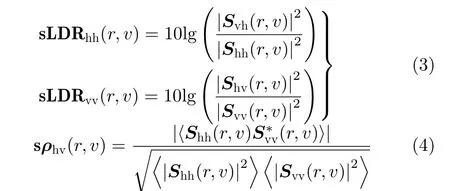
式(4)中 〈·〉表示对信号多普勒维进行1维高斯滑动平均操作。
由上述式(2)—式(4)定义可见,基于RD谱定义的谱极化参数综合了目标的极化信息和多普勒频率信息,还包括了目标的动态信息,更有利于区分气象目标和非气象目标。
3 SPP滤波器设计
为了能够有效去除杂波,同时保留尽可能多的气象信息,本文设计了一种基于谱极化参数的杂波滤波方法,SPP滤波器为RD域内的一个2元掩模,它可以根据气象和杂波在RD域内的特征不同进行前者的保留和后者的抑制。SPP滤波器的设计包含以下4个部分。
(1) RD域掩模生成。设置阈值,对谱极化参数进行阈值滤波,得到初步的2元掩模。2元掩模作用于原始回波的RD谱数据,它可以提取气象信息,屏蔽杂波信息。双极化气象雷达通常为STSR或ATSR工作模式,STSR工作模式下只能得到Vhh和Vvv共极化电压信号,ATSR工作模式下可以得到Vhh, Vvv共 极化电压信号和Vhv, Vvh交叉极化电压信号。所以按照雷达工作模式,分为两种情况来处理:
当雷达工作模式为STSR时,对谱相关系数sρhv进行阈值滤波。假设获得的2元掩模为Msρ,Msρ是 大小为Nr×NDwell的 矩阵,矩阵元素msρ∈Msρ取值为
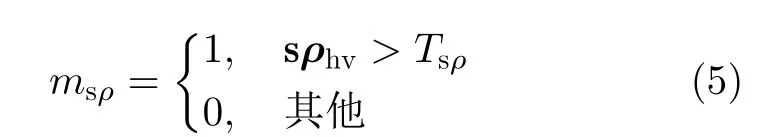
其中,“1”对应保留气象目标,“0”对应去除杂波。 Tsρ为谱相关系数阈值,可以根据杂波和气象目标的特性设置。气象目标的s ρhv值一般远大于除地杂波以外的其他杂波的s ρhv值,而地杂波和气象目标的s ρhv值分布区间大致相同,因此需要进一步采用其他方法抑制地杂波。
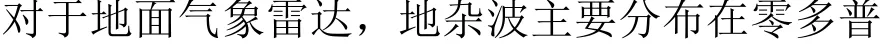

需要指出的是,掩模生成采用的阈值滤波处理可能会滤除弱气象信息,并有部分杂波剩余,在后续处理中需要考虑如何改善。
(2) 基于形态学方法的气象信息恢复。数学形态学在二值图像中有广泛的应用[19],本文采用闭运算来恢复缺失的气象目标信息。形态学闭运算可以填充二值图像内的小孔,弥合小裂缝,并保持总的位置和形状不变。经过算法第(1)步滤波后,气象目标内部回波强度比较弱的区域会有一些缺失,基于气象目标在RD域内具有连续性的特征,所以形态学闭运算可以填充这些缺失的气象信息,而不会过度填充出现虚假气象。闭运算是利用结构元素对二值图像先膨胀后腐蚀。由于圆盘对气象边界的平滑效果较好,本文将结构元素选为半径为R 的圆盘。
对 Mstep1进行闭运算后,获得新的2元掩模Mstep2,该掩模增强了对弱气象目标的保留。
(3) 标记对象,生成对象掩模。利用泛洪填充算法[20]将Mstep2中具有相同值“1”的连续区域标记为独立的对象。对2元掩模Mstep2进行处理,未被标记的值为“1”的点和其相邻区域将被标记为一个独立的对象,基于气象目标在RD域的连续性,本文采用8-领域像素填充法进行标记。对RD域标记结束后,按照对象面积降序排列,得到对象集合O =[O1,O2,···,ON,···], O同时包含了气象对象与杂波对象。每个对象Oi∈O, 都对应一个大小为Nr×NDwell的2元对象掩模MOi。
一般情况下,气象对象有两个性质:对象面积大和对象个数有限性。因此,选择对象集合O 中前 N个对象即包含了所有气象目标,然后再进行下一步处理。
(4) 筛选出所有气象对象。逐个提取对象集合O中的前 N个对象,经过筛选后将其归类为气象对象或杂波对象。如果选择的对象同时包含气象和杂波,说明气象目标和杂波此时具有相似的谱极化参数值和面积,形成的掩模不具有区分性。为了进一步去除杂波,需要利用谱宽值进一步筛选。


MSPP是作用于原始谱功率的2元掩模,用于去除杂波和噪声,并保留尽可能多的气象信息。
图1给出了SPP杂波抑制滤波器设计的流程图。由图1可知,SPP滤波算法是对每一个径向数据进行处理,在进行下一次径向扫描的同时可处理上一次径向扫描的数据,能够并行处理,具有较好的实时性。此外,SPP滤波算法一开始就在RD域生成一个初步的滤波掩模,后续的步骤都是对滤波掩模进行调整,整个滤波过程只有4步,且每一步都是简单的“0”和“1”操作,计算复杂度较低。
4 SPP滤波器参数选择
4.1 谱极化参数阈值选择
在选择谱极化参数的阈值时,完全保留气象信息和去除所有杂波往往会有冲突。阈值 TsLDR和Tsρ是根据气象目标和杂波去除的比例[15,21]选取的。除此之外,针对地面气象雷达,为了抑制地物杂波,使用零多普勒速度附近的凹口滤波器生成MGC。根据经验数值,静止地物杂波的多普勒速度主要分布在 –0.5~0.5 m/s。
4.2 圆盘半径选择
利用形态学方法进行气象信息恢复时,选择半径为 R的圆盘作为形态学闭运算的结构元素。为了确定 R的大小,首先设定真实气象区域,然后按照第3节所述的(1)和(2)对原始谱功率 sP(r,v)进行处理。
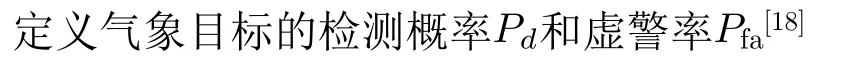

4.3 谱宽阈值选择
为了得到所有气象对象掩模,根据气象对象的两个性质(对象面积大和对象个数有限性),在这里只选择对象集合 O 中前 N个对象对应的掩模进行处理, N的选取准则为前 N个对象应包含所有的气象对象。计算前 N 个对象掩模MO1,MO2,···,MON中值为“1”的像素点总数Pobject,基于形态学进行气象信息恢复后的2元掩模Mstep2中值为“1”的像素点总数为 Pstep2,当Pobject/Pstep2≥90%时就认为得到的前 N个对象包含了所有的气象对象。根据这个原则,一般当N =8时即可满足这个条件,也可以根据数据的不同进行微调。谱宽阈值Tobject为

其 中,R 为圆盘半径大小,L 是杂波的最大谱宽。
5 实测数据验证
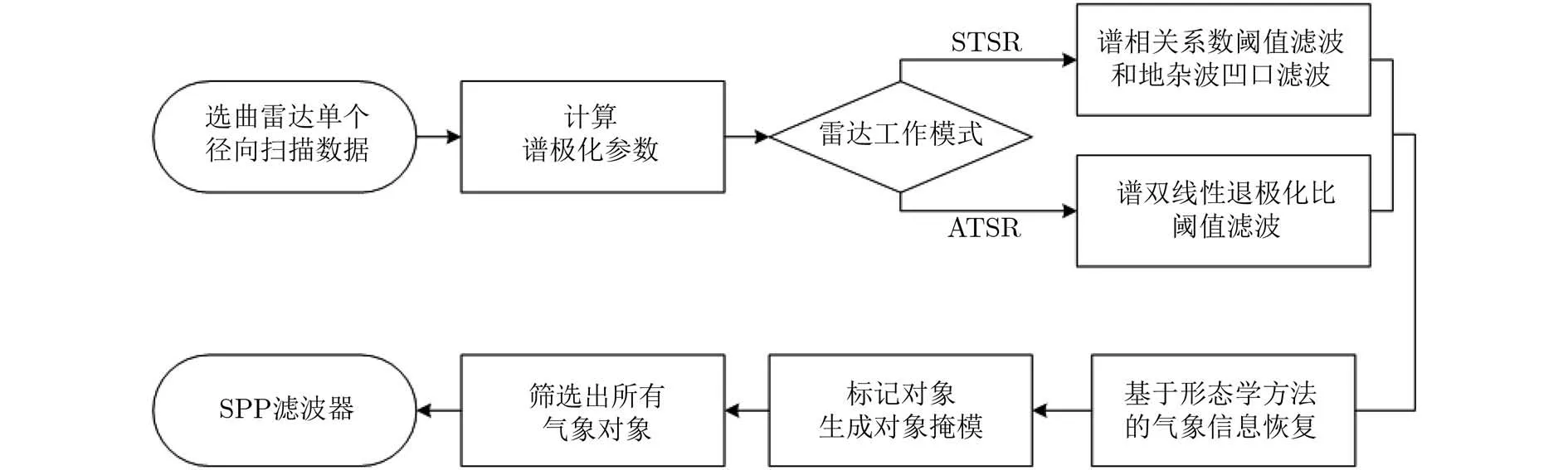
图1 SPP滤波器设计流程图
为验证本文所提杂波抑制方法的有效性,采用X波段和C波段气象雷达数据进行处理,其中X波段气象雷达工作模式为ATSR,有交叉极化测量,一个方位上的驻留脉冲数 NDwell=512, C波段气象雷达工作模式为STSR,不包含交叉极化测量,驻留脉冲数 NDwell=43。为了说明本文方法在杂波抑制和气象保留方面的优良性能,在ATSR模式下选取MDsLDR滤波方法[15]与本文算法进行比较,在STSR模式下选取传统的基于时域的门限因子杂波抑 制法[22]进行比较。
5.1 X波段ATSR极化气象雷达杂波抑制
5.1.1 谱极化参数分析
由一个径向扫描数据得到的谱极化参数如图2所示,图2(a)和图2(b)分别为谱功率 sP和谱线性退极化比s LDRhh。
从图2(a)可以看出该径向扫描数据包含气象目标、地杂波和条带状杂波。通过对多个径向扫描数据分析,发现条带状杂波具有以下特点:(1)多普勒速度不为0;(2)在RD域内随机出现,每个径向观察到的多普勒速度都不同;(3)强度和气象目标强度相当。这些增加了杂波抑制难度。
由图2(b)可见,气象目标的s LDRhh值明显小于杂 波的s LDRhh值。
5.1.2 滤波参数确定
根据气象目标和杂波去除的比例[15,21],并结合图3气象和杂波的s LDR概率密度函数(Probability Density Function, PDF)分布图,气象目标的sLDR值主要分布在–7 dB以下,杂波的s LDR值都比较大主要分布在–7 dB以上,所以取TsLDR=−7 dB。
选取图2(a)的数据,根据式(9)计算得到的Pd和Pfa与圆盘半径R 之间的关系如图4所示。由图4可知,当半径 R在[1, 3]区间时,Pd增长较快,Pfa增长较慢;当 R 在[3, 7]区间时,情况相反。R=3时, Pd与Pfa之间的差值达到最大值,因此设置圆盘半径。
根据数据统计,并结合图2(a),该数据的杂波最 大谱宽L =5 ,根据式(11)计算得到Tobject=11。
5.1.3 杂波抑制结果分析
一个径向扫描数据在RD域生成SPP滤波器的过程如图5所示。
在图5(a)中,经过 sLDR阈值滤波后残留了部分杂波点和条带状杂波,且气象区域内部和边界均存在缺失点。运用形态学闭运算,从图5(b)可以看出气象区域得到了恢复。图5(c)—图5(g)为标记的前5个对象,由图5(g)可知从第5个标记对象开始只包含了杂波对象。图5(h)为SPP滤波掩模。
对图2(a)的原始谱功率分别进行MDsLDR滤波和SPP滤波,得到图6所示的结果。对比图6(a)和图6(b),不管是与气象目标分开较好的地物杂波,还是与气象目标重叠的条带状杂波,两种滤波器都可以有效地去除。但是在3~5 km处,MDsLDR滤波算法在抑制条带状杂波同时造成了弱气象目标的抑制,如图中圆圈所示,所以在保持弱气象方面SPP滤波器效果更好。
5.2 C波段STSR极化气象雷达杂波抑制
与5.1.2节类似,可以确定s ρhv阈值为Tsρ=0.6,

图2 X波段气象雷达数据在方位角为261.9°时的谱极化参数
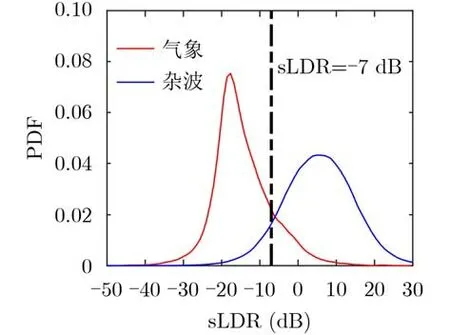
图3 气象和杂波的s LDR概率密度分布图

图4 圆盘半径大小与P d 和P fa的关系
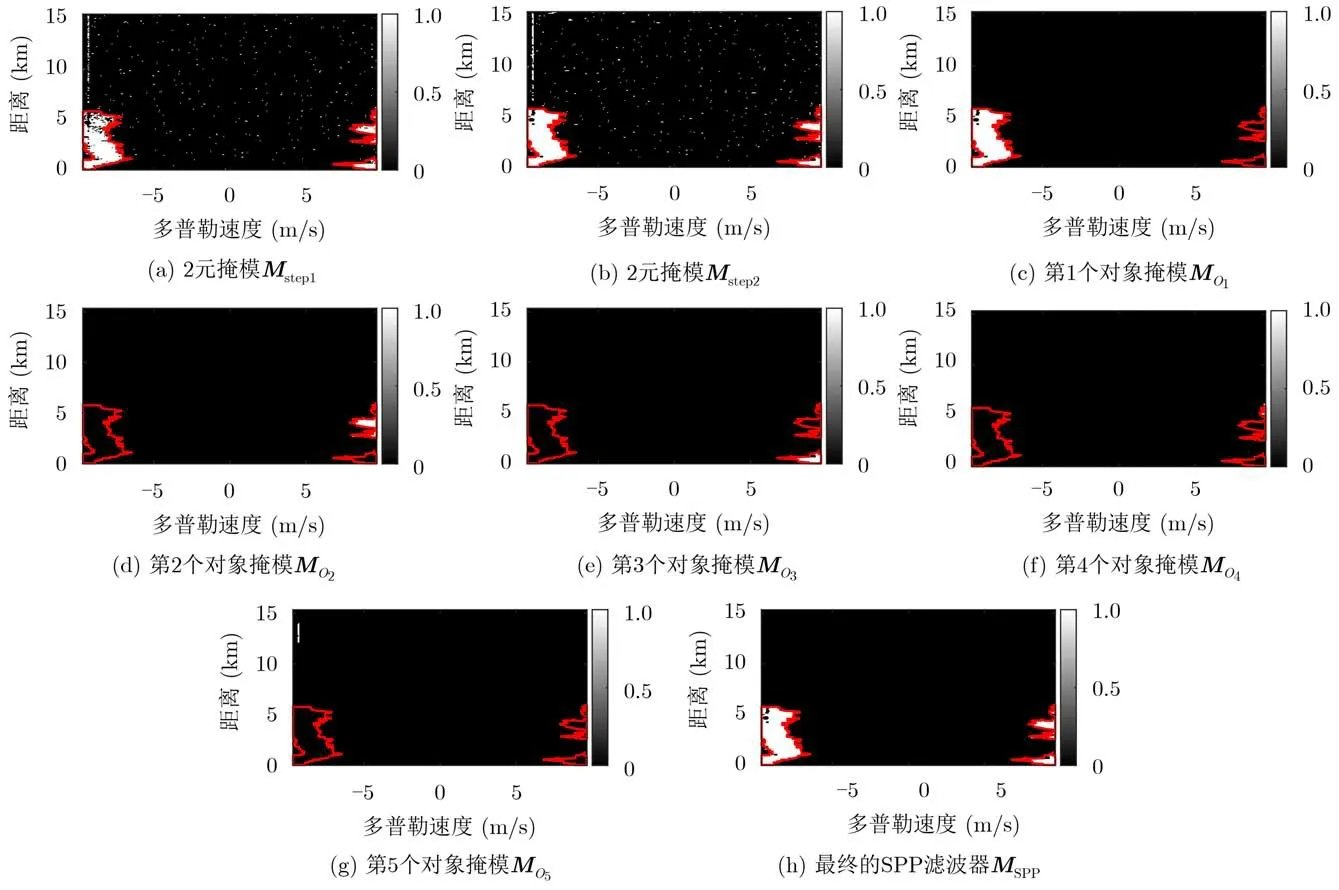
图5 X波段气象雷达一个径向扫描数据生成的滤波掩模
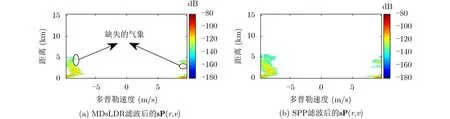
图6 滤波处理后的谱功率sP(r,v)
地杂波凹口滤波长度LGC=3 ,圆盘半径R =1,杂波最大谱宽 L=3,根据式(11)计算得到谱宽阈值Tobject=5。
针对一个径向扫描数据按照本文算法进行处理得到如图7所示结果。图7(a)中白色区域代表杂波抑制后的气象区域,红色轮廓包围区域代表真实气象区域。
图7(a)为生成的SPP滤波器,图7(b)为原始谱功率,图7(c)为SPP滤波后结果。图7(c)中零多普勒速度附近的空白值表示抑制的地杂波,该宽度取决于地杂波的多普勒速度分布区间,因为地物是静止目标,所以其速度一般分布在–0.5~0.5 m/s。气象目标(下落的雨滴、雪花等)普遍具有多普勒速度,只有很少一部分分布在零多普勒速度附近,所以对气象目标强度的影响可以微乎不计。对比图7(b)和图7(c)可以看出该滤波器可以有效地去除杂波,最终只保留气象信息。
5.3 杂波抑制前后反射率因子比较
C波段和X波段气象雷达数据经过SPP滤波后的反射率因子如图8和图9所示。
图8(b)与图8(c)分别为基于时域的门限因子杂波抑制和SPP滤波处理后的反射率因子。对比图8(a)的原始反射率,两种方法均能够有效地去除杂波。图8(b)中黑色椭圆圈标注区域表示时域处理结果缺失了部分弱气象信息,在保留弱气象方面性能比SPP滤波器差。
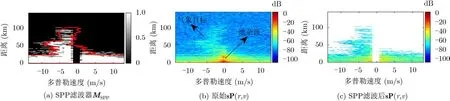
图7 C波段气象雷达数据在方位角为244.1°时利用本文算法处理结果
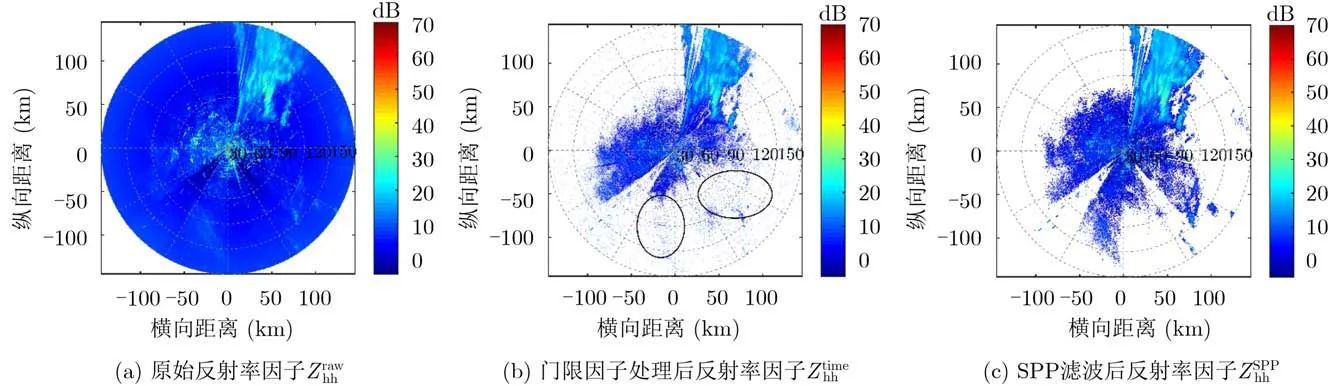
图8 C波段气象雷达数据反射率因子估计
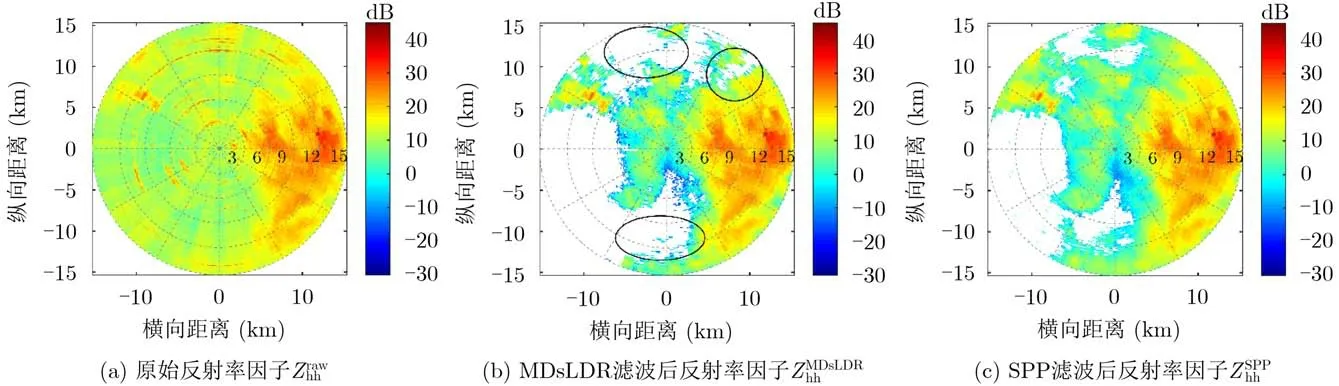
图9 X波段气象雷达数据反射率因子估计
图9(b)与图9(c)分别为X波段气象雷达MDsLDR滤波和SPP滤波处理后的反射率因子,图9(b)中黑色椭圆圈标注区域表示MDsLDR滤波结果缺失了部分弱气象信息,由此可见,SPP滤波器在保留弱气象信息方面的性能优于MDsLDR滤波器。
6 结论
针对双极化气象雷达中非气象回波滤除问题,本文提出一种基于谱极化参数的杂波滤波方法。根据气象和杂波在RD域内的特征不同进行前者的保留和后者的抑制。首先利用气象目标的频谱极化特征和连续性构造谱极化参数,结合形态学方法,在RD域内生成一个2元掩模。然后采用面向对象的思维,将2元掩模标记为气象对象掩模和杂波对象掩模。最后引入谱宽值作为额外的参数,筛选出所有气象对象掩模并叠加得到SPP滤波器。对原始谱功率应用SPP滤波器,可以保留气象,去除杂波和噪声。气象雷达实测数据杂波抑制结果验证了本文方法的有效性。结果表明,本文方法适用于不同工作模式的双极化气象雷达,与MDsLDR滤波器和基于时域的门限因子杂波抑制方法相比,具有较好的杂波抑制效果和气象保留性能。SPP滤波器实现简单,计算复杂度低,可以实时应用于双极化监视气象雷达,且为机载极化气象雷达杂波抑制算法奠定了基础。
