顾及层析区域外测站的GNSS水汽层析建模方法

赵庆志，姚宜斌，姚顽强

1. 西安科技大学测绘科学与技术学院，陕西 西安 710054； 2. 武汉大学测绘学院，湖北 武汉 430079

水汽是对流层中最重要的大气组分之一，对洪水、台风、冰雹等多种自然灾害的形成具有重要影响[1]。精确的水汽信息是开展天气预报服务和气象研究的先决条件[2-4]，然而，鉴于水汽的时空复杂性和多变性，高精度多维水汽信息的获取目前仍是一项极具挑战的工作[5-6]。

现有水汽探测技术根据传感器搭载平台不同可分为星基、地基和空基水汽探测[7-10]。自全球导航卫星系统(global navigation satellite system,GNSS)气象学发展以来[11]，GNSS水汽探测已被证明是获取大气水汽最具潜力的方式之一。GNSS水汽探测大气可降水量(precipitable water vapor,PWV)精度达到1～2 mm[12]。然而，PWV是测站在不同高度角和方位角的卫星射线方向上的水汽含量投影到天顶方向上的均值，并不能直观有效地反映地面测站周围水汽的变化。因此，文献[13]提出了GNSS对流层水汽层析的概念，以获得测站附近的三维水汽分布信息。文献[14]首次利用GPS网实现了水汽层析试验。

水汽层析技术是将层析区域在水平和垂直方向上离散成若干个体素，并假设每个体素内的水汽密度在给定时间内为一常数，然后，通过对穿过该区域卫星信号上的水汽进行积分，构建水汽观测方程。由于卫星星座几何分布的特定性，卫星射线穿过层析区域时呈倒穹顶分布，导致大量体素内并没有射线穿过，特别是在层析区域的下方和侧面[14-15]。因此，观测方程的求解是一个不适定问题[16]。为了解决该问题，需要加入一些先验信息或物理条件来约束水汽信息的空间分布[17-19]。近年来，随着水汽层析技术的发展，国内外先后提出了附加虚拟信号[20]、动态调整模型边界和节点[21]、顾及GNSS侧面穿出射线[22-23]、合理选取GNSS权值信息[24-25]、采用非均匀格网划分[26-27]、引入粒子群优化算法[28]、联合地基和空基GNSS[29]、联合多源水汽信息[30-32]等方法来提高三维水汽反演结果的精度和可靠性。

然而，上述研究均未考虑利用层析区域外测站数据构建三维水汽层析模型，导致层析区域边界水汽反演精度较低、可靠性较差。随着地基GNSS广泛应用于导航、定位、地震监测和天气预报等方面，我国已建成了高密度的地基GNSS观测网。据不完全统计，目前我国已安装地面GNSS接收机超过5000余台，相邻两站平均距离小于50 km。因此，如何充分利用层析区域外测站的观测数据构建水汽观测方程，实现顾及研究区域外测站数据的高精度三维水汽反演是亟待解决的难题，对于有效增加射线穿过体素的数量，改善层析法方程结构的稳定性等都具有重要意义。

本文针对上述问题，提出一种顾及层析区域外测站的GNSS水汽层析建模方法。GPT2w模型是目前经验模型中精度较高的模型之一，能够提供任意位置的气象数据，如气温、气压和水汽压等，且输入信息只需要测站经纬度和高程[33]，因此，首先基于GPT2w模型计算层析区域每个体素内的水汽密度初值，然后引入比例系数，构建层析区域外测站数据的水汽观测方程，并附加到传统层析模型中。利用浙江省CORS网络的数据对该方法进行试验，证实本文方法优于传统层析方法。

1 水汽层析基本原理

GNSS层析建模时输入信息包括斜路径湿延迟(slant wet delay,SWD)和斜路径水汽含量(slant water vapor,SWV)两类，分别可以获取层析区域每个体素内的湿折射率和水汽密度[14,26,34-35]。上述两类层析结果可以根据大气温度场进行相互转换[36]。本文以SWV为输入信息构建层析观测方程。

1.1 层析观测方程构建

由于大气水汽的影响，当GNSS卫星信号穿过对流层时会产生折射和弯曲，该类延迟被称为对流层延迟，可以表达成如下形式[14]

(1)

式中，Nw表示湿折射率；l表示信号从接收机到卫星的距离。SWD根据式(2)可一步转化成SWV[26]

(2)

式中，ρv表示水汽密度；Rw、k3和k2为常数，其值分别为461 J/Kg/K、3.776×105K2/hPa和16.48 K/hPa；Tm为加权平均温度。

利用GNSS观测值和气象参数计算得到SWV后，一条卫星信号上的水汽层析观测方程的积分形式可表达为

SWV=∑ijk(dijkρijk)

(3)

式中，i、j和k分别表示层析区域在经度、纬度和高程方向上划分的体素个数；d表示卫星信号在体素内的距离；ρ表示体素内未知的水汽密度参数。因此，多条卫星信号上的水汽观测方程的矩阵形式可表示为

y=Ax

(4)

式中，y表示层析区域内测站上完整穿过研究区域的SWV观测数据构成的列向量；A表示卫星信号在每个体素内的距离构成的设计矩阵；x为未知的水汽密度构成的列向量。

1.2 约束方程构建

由于卫星空间几何结构的特定性，某些体素内没有卫星信号穿过，导致建立的层析观测方程秩亏。通常，需要加入约束信息来解决该问题。本文通过加入水平约束、垂直约束和先验约束条件来构建传统层析观测模型。

在构建水平约束方程时，提出了一种水汽加权平均值的方法[37]，即某一体素内水汽密度值可以表示为其周围多个体素内水汽密度值的均值，如下式

h1x1+h2x2+…+hj-1xj-1-xj+hj+1xj+1+

…+hmxm=0

(5)

式中，hi表示体素i在水平方向上的加权系数；xi表示未知的水汽密度；m表示同一水平面内总的体素个数。

构建垂直约束时，根据水汽随高度呈现总体递减的趋势，利用指数函数来描述水汽的垂直变化[27]

(6)

式中，hi表示第i层对应的高度；H表示水汽比高，其经验值取1～2 km，可通过无线电探空数据或ECMWF数据拟合得到。

对于先验约束，利用层析试验前3 d探空数据获取的水汽密度初值作为先验值。本文只针对无线电探空站所在位置及其垂直方向上的体素进行先验约束。联合上述3类约束信息和水汽观测方程，可得到传统层析模型的矩阵形式

(7)

式中，H、V和Ap分别表示水平、垂直和先验约束的系数矩阵；yp表示利用探空数据计算的水汽密度初值。

2 顾及层析区域外测站数据的层析模型构建

层析模型中只有观测方程是根据实测SWV构建，层析结果的精度很大程度上取决于层析观测方程构建的质量[35]。因此，利用尽可能多的SWV构建层析观测方程是获取高精度三维水汽信息的关键。但传统层析模型中，只能利用完整穿过层析区域的观测数据构建水汽观测方程，图1中，只有r0接收机的观测数据(实线)可以利用，而忽略了接收机r1和r2中观测数据(虚线)对层析结果的影响。

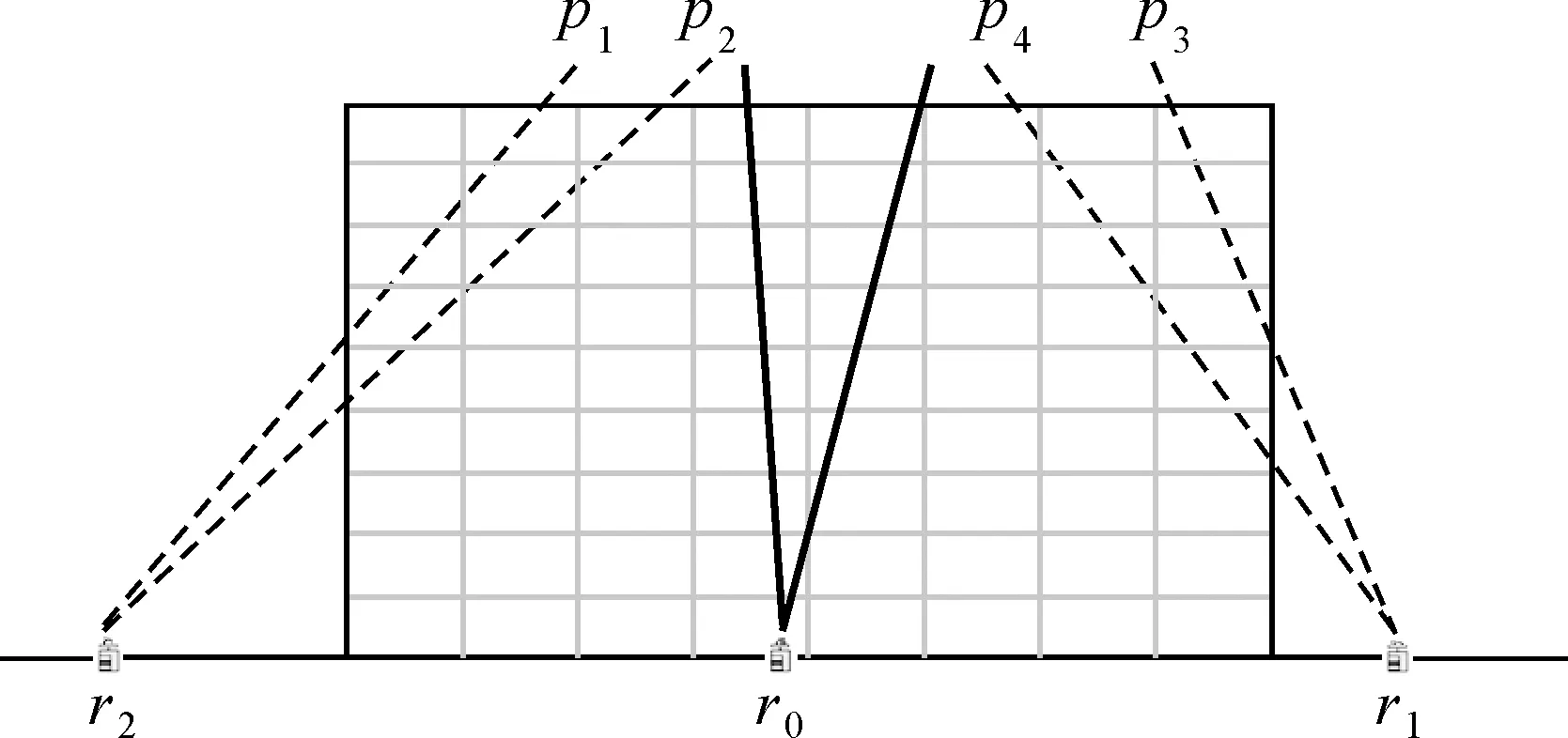
图1 卫星信号穿过层析区域Fig.1 Schematic diagram of satellite signals cross the tomographic area

为了克服传统层析模型无法利用如图1中r1和r2接收机观测数据的缺陷，本文提出了一种顾及层析区域外测站数据的三维水汽建模方法。首先，通过GPT2w模型计算每个体素内的水汽密度初值；然后，引入比例系数并联合水汽密度初值建立相应的比例系数模型；最后，确定层析区域外测站上的观测数据在层析区域内的水汽含量，并构建相应的水汽观测方程。图2给出了顾及层析区域外测站数据的水汽观测方程构建原理，具体步骤如下。

(1) 基于GPT2w模型计算层析区域每个体素内的水汽密度初值。根据水汽状态方程，水汽密度初始值ρ0计算公式如下

ρ0=e/(RvT)

(8)

式中，e、T分别表示水汽压和温度；Rv为常数，其值为461.5 J/kg/K。

(2) 选取辅助区域并计算比例系数，表示信号在层析区域内上的水汽含量与该条射线上水汽总含量之比，比例系数的具体计算如下：

① 选取层析区域中心为原点，以确定的步长在经纬方向上扩展辅助区域，直至接收机A(图2中黑色三角形)包含在辅助区域内。通过上述方法，确定如图2中的3个辅助区域，信号AS与3个辅助区域有P、M和L3个交点。

② 信号AS被辅助区域1划分为AL和LS两部分，可以根据水汽密度初值和信号在每个体素内的截距计算LS射线上的SWV，如下式

(9)

因此，射线AS的一个比例系数SCLS为

(10)

式中，SWVAS表示信号AS上总的水汽含量。利用上述方法，可以分别计算AS对应的另外两个比例系数SCMS和SCPS。

③ 利用步骤②计算接收机A上所有卫星信号的比例系数。

④ 重复步骤②—③，获取所有接收机观测卫星信号所对应的比例系数。

(3) 建立比例系数模型。通过对比例系数进行分析，发现该系数与信号和辅助区域侧面交点的高(如图2中hLR、hMN和hPQ)存在指数负相关关系(后文具体讨论)。因此，构建如下模型

SC=a0+a1exp(1/h)

(11)

式中，a0和a1表示比例系数模型的系数；h表示信号和辅助区域侧面交点的高。本文中，由于每一历元SWV的值不同，估计的模型系数a0和a1在每次层析解算中均不断更新。

(4) 计算层析区域外测站信号在区域内上的水汽含量。对于层析区域外的测站信号(如图2中射线WB)，其对应的一个比例系数SCWE可根据步骤(3)中构建的模型和射线与层析区域侧面交点的高计算得到

SCWE=a0+a1exp(1/hEF)

(12)

因此，层析区域外测站信号在层析区域内上的水汽含量SWVWE可利用SCWE和射线BE上的水汽含量SWVBE计算得到

SWVWE=SCWESWVBE

(13)

(5) 联合顾及层析区域外测站数据构建的观测方程式(13)和传统层析模型式(7)，可得到本文提出的层析模型

(14)

式中，Aout和yout分别为利用层析区域外测站SWV数据构建的观测方程的设计矩阵和式(13)中计算的水汽含量构成的列向量，其中Aout和A中观测方程的表达形式相似，如式(3)所示。式(14)中方程的维数随着观测方程个数的变化在不同历元不同，n表示待估参数的个数，其值等于层析区域内离散化的体素总数。

(6) 利用最小二乘方法对式(14)进行解算，求得未知的水汽密度参数[14,26]

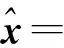
(15)

式中，PA、PH、PV、PAp和PAout分别表示不同类型方程的权阵。本文通过联合方差分量估计和Bartlett检验方法获取不同类型方程权阵[37]。

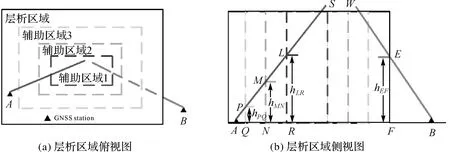
图2 顾及层析区域外测站数据构建层析模型的原理Fig.2 Schematic diagram of the proposed method using the signals derived from receivers outside the tomographic area

3 验证与分析

3.1 试验描述与数据处理

为了验证本文提出方法获取三维水汽的精度，选取浙江CORS网中24个地基GNSS站2015年年积日121—143共23 d的数据进行试验。其中，12个GNSS站位于层析区域内，另外12个GNSS站位于层析区域外，如图3中所示。此外，选取位于层析区域内的无线电探空站(58 457)对层析结果进行验证。层析区域范围在经纬度和高程方向上分别为119.55°E—120.75°E、29.90°N—30.80°N和0～10.4 km。根据经验将层析区域划分为6×6×13个体素，在经纬度方向上的步长分别为0.15°和0.2°，在垂直方向上的步长为0.8 km，层析试验的时间步长为0.5 h。本文共设计两种试验方案：

方案1，利用传统层析模型(式(7))反演水汽，即只利用层析区域内12个GNSS站的观测数据。

方案2，利用本文提出的顾及层析区域外测站数据构建的层析模型(式(14))反演水汽，即利用选取的24个GNSS站的观测数据。

本文利用GAMIT/GLOBK(v10.5)软件对GNSS观测数据进行处理[38]，ZTD和梯度项每隔0.5和2 h估计一次。天顶静力学延迟(zenith hydrostatic delay，ZHD)根据Saastamoinen模型利用实测地表气压计算得到[39]，然后进一步获取天顶湿延迟(zenith wet delay,ZWD)。因此，根据映射函数和气象参数可以计算得到SWV[14]。进行GNSS数据处理时，区域网中卫星信号传播路径相似，对流层参数存在强相关性。为了获取绝对对流层参数，引入3个IGS站(AIRA、CHAN和LHAZ)进行数据联合处理[41]。此外，为了消除信号弯曲对层析结果的影响，本文选取卫星截止高度角大于10°的卫星信号进行试验[41]。

图3 试验区域地基GNSS分布Fig.3 Distribution of the ground-based GNSS stations selected in the experiment

3.2 比例系数模型分析

如前文所述，比例系数与高程存在指数负相关关系。因此，首先对二者的关系进行验证。图4给出了选取试验区域内比例系数随高度变化及不同年积日内比例系数模型的RMS。比例系数模型的RMS利用试验时段内模型计算的比例系数和实测数据计算的比例系数计算得到。由式(13)可以看出，建立的比例系数模型精度对SWV的计算有直接影响。通过对23 d的试验数据分析，发现建立的比例系数模型的最大RMS小于0.15，其均值约为0.05，平均RMS为0.096。通过统计，试验时段内层析区域外测站信号上的水汽含量的均值为60 mm，因此，利用式(13)计算的SWV值的平均误差在5.8 mm左右。

3.3 IWV对比

为了对本文方法进行验证，首先对两种试验方案的数据利用率及有信号穿过的体素数进行统计。图5给出了试验时段内每天信号利用情况及有信号穿过的体素数的百分比。由图5可以看出，方案2在信号利用率及有信号穿过的体素百分比方面均优于方案1。对23 d的结果进行统计，发现相对于传统层析方法(方案1)，本文方法(方案2)的信号利用率增长了26.8%，有信号穿过的体素数增长了14.9%。上述结果也间接证明了本文方法能够改善水汽层析模型的不适定性。

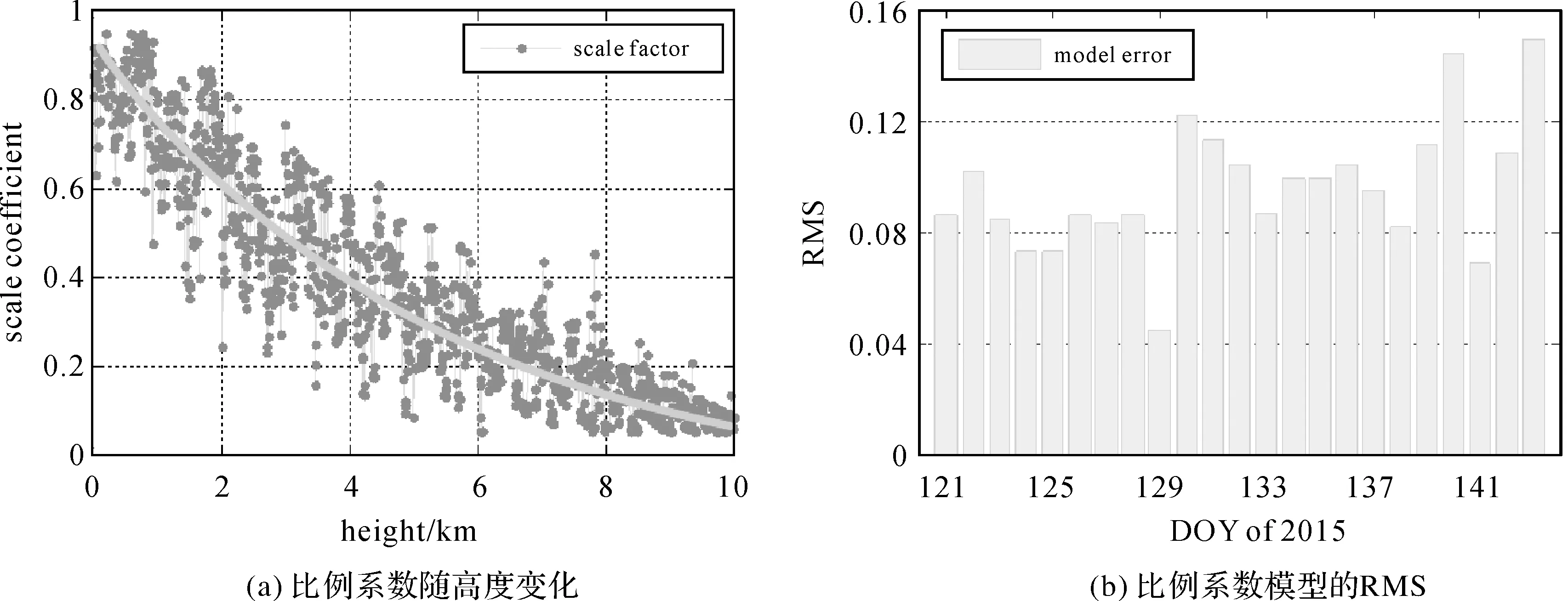
图4 比例系数的统计分析Fig.4 Statistical analysis of scale coefficient

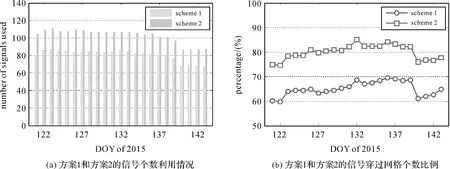
图5 试验时段内不同方案卫星信号利用数和有信号穿过的体素数的对比情况Fig.5 Number of signals used and the percentage of voxels crossed by satellite rays for two schemes over the test period

此外，以无线电探空数据计算的综合水汽含量(integrated water vapor,IWV)为真值，对两种方案反演的水汽密度计算的IWV在UTC 00:00和12:00历元进行对比。图6给出了试验时段内无线电探空和两种层析方案计算得到的IWV时间序列。由图6可以看出，两种方案反演水汽密度计算的IWV与探空数据计算结果具有很好的一致性。但通过对两种方案计算的RMS、Bias和平均绝对偏差(mean absolute error,MAE)进行统计(表1)，发现方案2的结果优于方案1。方案2获取IWV的RMS/bias/MAE分别为4.2/0.4/3.5 mm，传统方法获取IWV的RMS/bias/MAE分别为4.6/0.8/3.7 mm。

图6 试验时段内不同方案计算的IWV与探空计算IWV的对比Fig.6 Comparison of IWV time series derived from radiosonde and two schemes over the experimental period

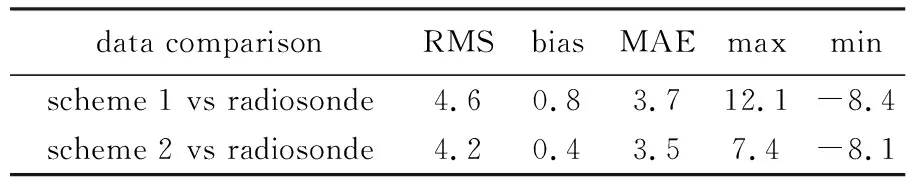
表1 不同方案计算的IWV与探空数据计算IWV的对比统计结果

3.4 水汽密度对比

IWV为不同高度上的水汽密度在垂直方向上的积分，并不能反映水汽在不同高度的时空变化。为了进一步验证本文方法的优越性，对两种试验方案获取的水汽密度在不同高度上进行对比。首先对两种方案在特定历元(UTC 00:00,DOY 138和UTC 12:00,DOY 141)的水汽廓线进行对比。选取上述两个历元进行对比是因为这两个历元的IWV分别对应试验时段内的最大值和最小值。图7给出了不同方案在两个历元水汽密度随高度的变化情况。由图7可以看出，相较于传统方法(方案1)，本文方法(方案2)反演的水汽密度在两个特定历元与探空数据计算的水汽密度较为接近，进一步验证了本文方法反演的水汽具有较高的精度。对试验时段内的结果进行统计，发现本文方法反演水汽密度的RMS/Bias/MAE在两个历元分别为1.3/-0.2/1.0 g/m3和0.8/0.1/0.6 g/m3，传统方法反演水汽密度的RMS/Bias/MAE在两个历元分别为2.0/-0.5/1.5 g/m3和1.2/0.5/0.8 g/m3。

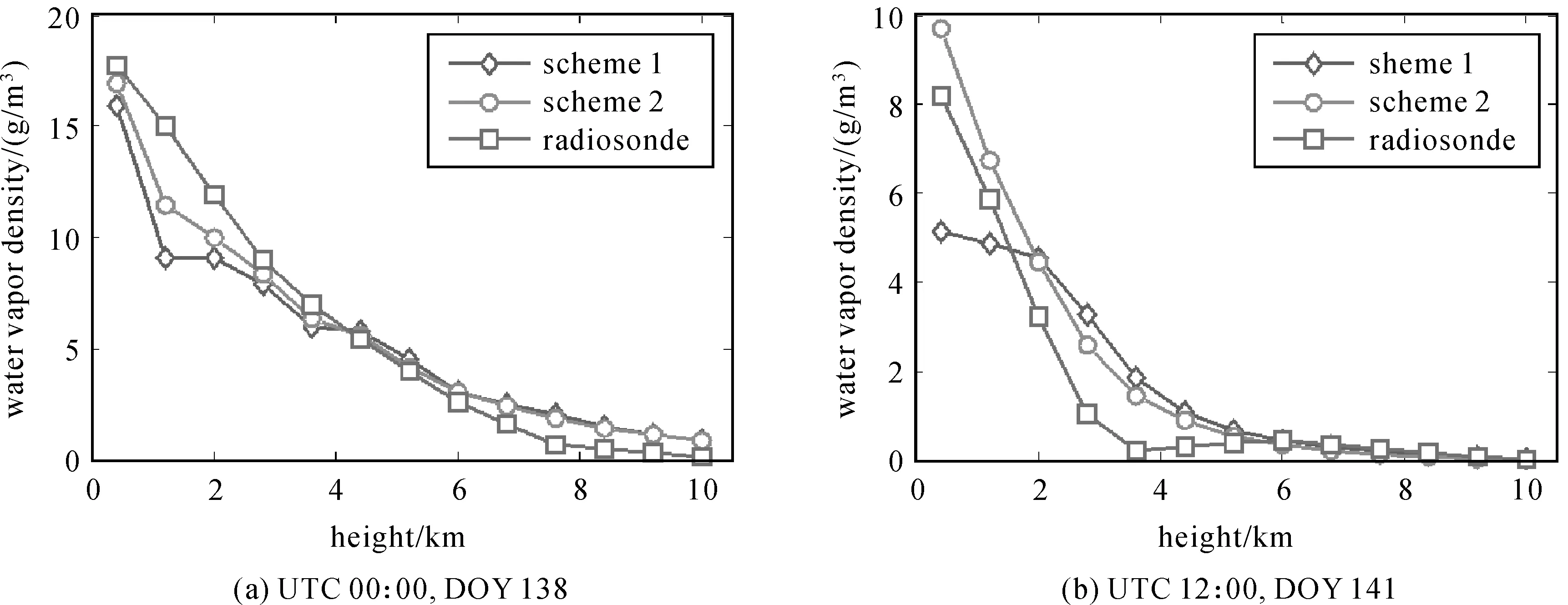
图7 试验时段内不同方案反演的与探空数据计算的水汽密度在不同高度上的对比Fig.7 Water vapor density profiles comparison at various altitudes between radiosonde and two schemes over the experimental period

此外，对试验时段内共23 d两种方案获取的层析结果进行验证，图8给出了两种方案反演水汽密度在每天的平均RMS和bias。RMS和bias利用不同方案反演得到的水汽密度与探空数据计算的水汽密度对比得到。由图8可以看出，本文方法(方案2)的RMS和bias在试验时段内几乎都小于传统层析方法(方案1)，其RMS和bias的均值分别为1.1和0.04 g/m3，传统层析方法的RMS和bias的均值分别为1.4和0.05 g/m3。上述结果进一步证实了本文方法优于传统层析方法。

最后，对两种方案获取的水汽密度在不同高度上进行对比，并计算两种方案的相对误差Re

(16)

式中，ρtomo表示不同方案获取的水汽密度；ρrs表示利用探空数据计算的水汽密度。试验时段共有23 d的数据，对每天UTC 00:00和12:00的数据进行对比，共有46对数据。图9给出了不同方案反演水汽密度的平均RMS和相对误差对比情况。由图可以看出，本文方法的RMS和相对误差在不同高度上均小于传统层析方法，其最大RMS为1.8 g/m3，而传统方法最大RMS为3 g/m3。上述结果证实，本文提出的顾及层析区域外测站数据的水汽反演方法获取的水汽密度在大多数层上均优于传统层析方法。

4 结 论

本文提出一种顾及层析区域外测站数据的三维水汽建模方法。首先，利用GPT2w模型计算层析区域每个体素内的水汽密度初值；然后，通过引入比例系数构建该系数与射线和辅助区域侧面交点高的函数模型；最后，利用该模型和层析区域外测站数据建立层析观测方程，并与传统层析观测模型联合反演水汽。

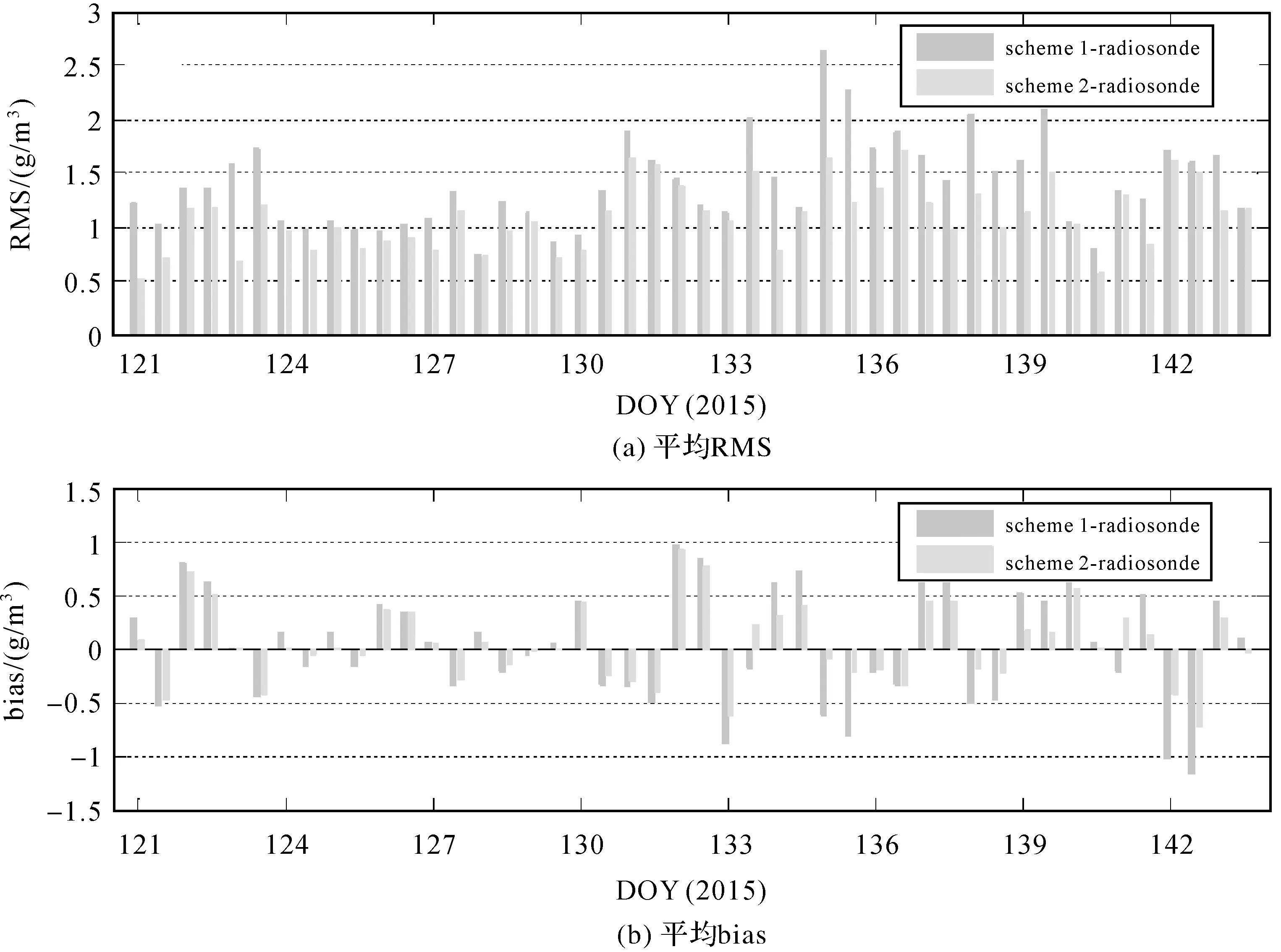
图8 试验时段内不同方案反演水汽密度的平均RMS和biasFig.8 Average RMS error and bias of water vapor density profile of two schemes over the tested period

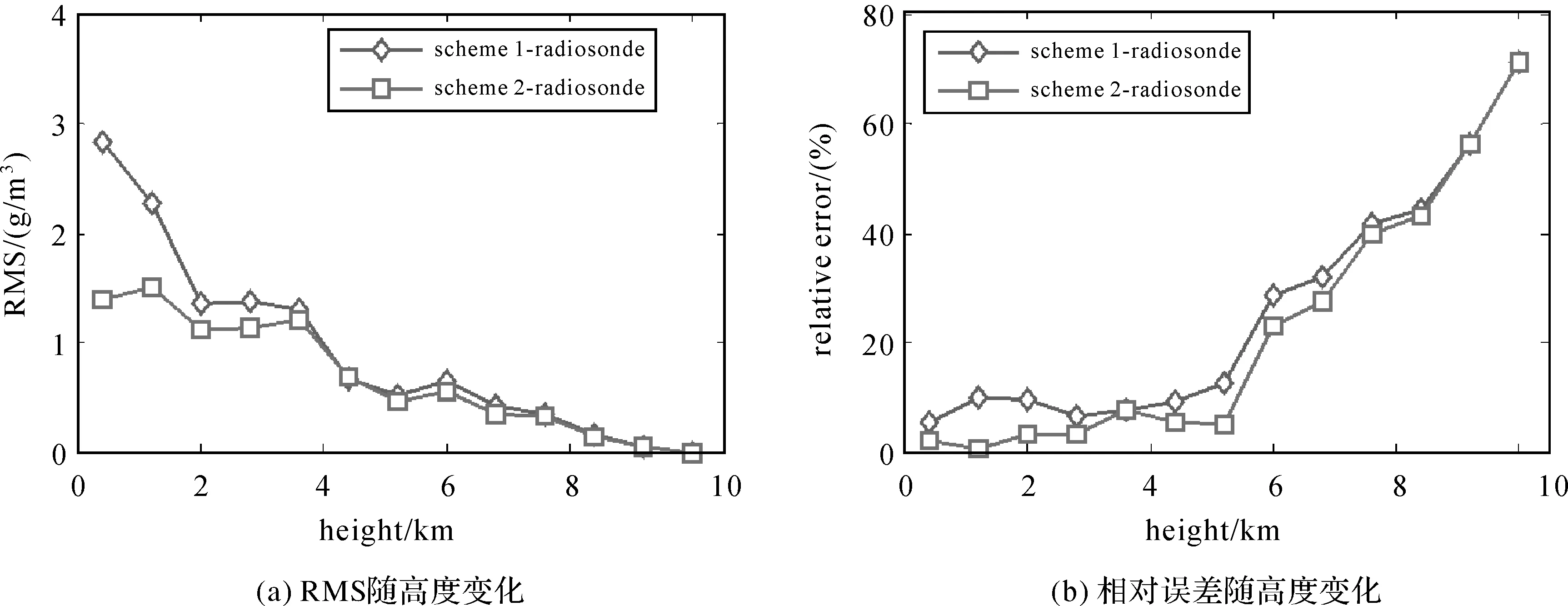
图9 2015年试验时段(年积日121—143)不同方案反演水汽的RMS和相对误差随高度变化Fig.9 RMS error and relative error change with height of different schemes over the experimental period of DOY 212—143, 2015

利用浙江CORS网中24个GNSS测站共23 d的数据对本文方法进行验证，并选取该区域内的一个无线电探空站进行对比。试验发现，比例系数模型的RMS为0.096，对SWV计算的误差约为5.8 mm。与传统方法对比，本文方法的GNSS数据利用率提高了26.8%，有射线穿过的体素数提高了14.9%。以探空数据为标准对本文提出层析模型的有效性及精度进行验证，结果表明：本文方法计算的IWV和反演的水汽密度均优于传统层析方法，改善率分别为8.7%和21.4%。

致谢：感谢IGRA提供的无线电探空数据和浙江省测绘地理信息局提供的CORS网数据。