利用射电天线轴线信息测定VLBI站点垂线偏差

马小辉，孙中苗，张志斌，张阿丽，袁 野，孙正雄，王 宏

1. 信息工程大学地理空间信息学院，河南 郑州 450001； 2. 西安测绘研究所，陕西 西安 710054； 3. 地理信息工程国家重点实验室，陕西 西安 710054； 4. 中国科学院上海天文台，上海 200030； 5. 中国科学院大学天文与空间科学学院，北京 100049； 6. 中国科学院新疆天文台，新疆 乌鲁木齐 830011； 7. 北京跟踪与通信技术研究所，北京 100094

垂线偏差(deflection of the vertical,DOV)的定义为地面一点上的重力矢量和相应椭球面上的法线矢量之间的夹角[1]。DOV在天文与大地成果(坐标、方位角)间的转换、观测水平角垂直角到椭球的归算、大地网平差、大地水准面检核、不同高程系统间的转换等方面有着广泛应用；在航天领域[2-3]以及地下物质迁移、地震信号分析等地球物理研究[4-9]领域也有重要应用价值。国际天文联合会[10]与国际大地测量协会[11]以及中国大地测量学学科发展战略研究组[12-13]等组织均对DOV的研究十分重视。

DOV的测定方法包括传统天文大地测量法[14]、GNSS水准法[15-16]、重力测量法[17]和地球重力场模型法[18-19]。天文大地测量法观测设备近年已由天顶筒升级为数字天顶仪[20]，内符合观测精度为～0.2″，轴线绝对定位精度为1～2″。GNSS水准法在采用相对精度为厘米级的大地水准面的情况下可获得～0.7″计算精度的DOV[21]，该方法适用于面积不大且地形呈线性变化的地区，DOV测定精度为几个角秒。采用重力测量法和地球重力场模型法，我国2000中国重力场与似大地水准面模型(CGGM2000)确定任一点DOV的精度可达1.5″。

甚长基线干涉测量技术(very long baseline interferometry，VLBI)观测站会在建站初期开展本地测量以测定VLBI天线参考点坐标初值[22]。观测站开展运行后，会对多技术并置站(如VLBI和GNSS)开展不定期本地连接测量。VLBI全球观测系统(VGOS)要求每两年半开展一次本地连接测量[23]，来测定VLBI天线参考点与其他空间大地测量设备参考点之间的连接矢量，从而对多技术地球参考架提供约束。VLBI测站需定期开展天线指向改正测量和天线归心测量，以保证天线的观测性能。但因VLBI技术对重力不敏感[24]，长期以来VLBI测站DOV测量需依托专用测量设备，如天文经纬仪、天顶筒、数字天顶仪和GNSS接收机等。鉴于VLBI测站对DOV测定需求的功能扩展，考虑依托本地归心测量中的水准信息，使得VLBI测量对重力信息变得敏感，从而进一步结合VLBI天线指向改正测量结果反演DOV信息。本文针对应用广泛的方位俯仰型天线，提出利用天线方位轴指向信息测定DOV的原理与方法，并利用已有数据对VLBI测站处DOV测定结果进行初步验证。

1 原 理

利用天线方位轴与本地垂线和法线的关系来测定VLBI测站DOV原理简单直观，如图1所示。图1(a)中，天线方位轴近似指向天顶；图1(b)中，通过对天线开展本地归心测量，观测与天线随动的靶标，再进行归心解算，不仅可以计算出参考点点位，而且可以确定天线方位轴与本地垂线矢量间的夹角u1；图1(c)中，通过开展天线指向修正测量，不仅可以构建天线指向修正模型保证天线指向精度，而且可以确定天线方位轴与本地法线矢量间的夹角u2；u1与u2之差即为该站DOV。

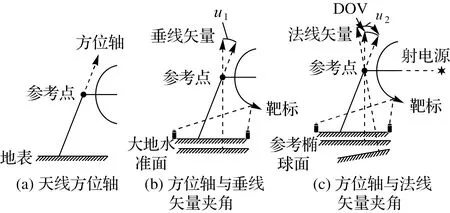
图1 利用天线归心测量与天线指向测量信息确定DOV的原理Fig.1 The principle of determining DOV by telescope local surveying and pointing calibration data

u1与u2分别基于天线归心测量模型和天线指向改正模型求出。一直以来，射电天线的归心测量工作与指向改正工作分别服务于站址标定和天线观测，两者分别独立开展，所采用模型中的轴系误差与正负角等定义并不相同，这在一定程度上限制了两者的测地推广与应用。为了获得可靠的u1与u2，天线归心测量模型与指向改正模型中的相关定义必须统一，这些定义包括轴系误差的类别、正方向及可合并误差项等。

2 统一的天线指向改正模型和归心测量模型

统一的天线归心测量模型与指向改正模型，是利用天线归心测量和天线指向改正产品(即u1与u2)计算DOV的前提。所谓统一是指将两个模型中的坐标系、正角负角以及轴系误差的定义保持一致。本节将分别对两者共用坐标系、正角负角以及轴系误差进行定义，并推导出统一的天线指向改正模型和归心测量模型。需要注意的是，本文的天线指向改正模型仅涉及因轴系误差而引起的天线指向改正(主项改正)，并不涉及大气折射、天线重力形变等指向改正(小项改正)。

2.1 本文定义

2.1.1 坐标系定义

本文共用到3套坐标系，分别为站心坐标系OENU、天线坐标系Oxyz以及天线指向切面坐标系OA′RE′，3套坐标系均为笛卡尔坐标系(右手系)，均以参考点为原点O，如图2所示。天线参考点定义为天线主动轴与包含从动轴运动平面的交点[25]，站心坐标系OENU3轴指向分别对应“东、北、上”方向，注意指向模型建模中的“上”近似于参考点相对参考椭球法线的反方向；天线坐标系Oxyz第1轴为天线俯仰轴x，第2轴为天线指向方向y，与两轴均垂直且过O点的为z轴；天线指向切面坐标系OA′RE′，第2轴R为天线指向方向，第1轴A′和第3轴E′分别对应方位和俯仰方向。

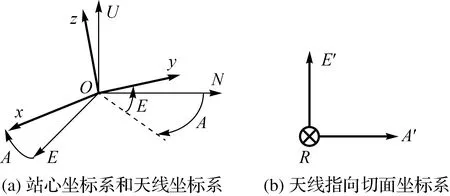
图2 三套坐标系示意图Fig.2 Three coordinate systems

本文所用旋转矩阵共两种，第1种用来描述质点在同一坐标系中的旋转，用R1/2/3表示，下标分别表示绕第1、2、3轴的旋转；第2种用来描述新坐标系相对旧坐标系的旋转，用S1/2/3表示，下标意义同上。

2.1.2 正角负角定义

笛卡尔坐标系中，坐标系旋转实质是轴系相对某一角度旋转，角度正方向符合右手准则，反之为负。本文涉及的正角包括α、β、γ、δ、μ和E；负角包括λ和A。

2.1.3 轴系误差定义

文中E和A分别表示天线俯仰角(或高度角)和方位角，各轴系误差名称与符号见表1。天线准直差反映了天线实际指向与设计指向在空间中的固定差异，δ表示该准直差在空间中的水平分量，其对方位角的影响ΔA随天线高度角不同而不同(见图3)；天线垂直指向准直差则与俯仰度盘差耦合，本文将其合并称为俯仰度盘差。表1中前6项统称为轴线倾斜，用角度来描述，后一项e为方位轴与俯仰轴间的轴线偏差，用距离来衡量。e的正向为天线的水平指向方向。

表1 各类轴系误差及其解释

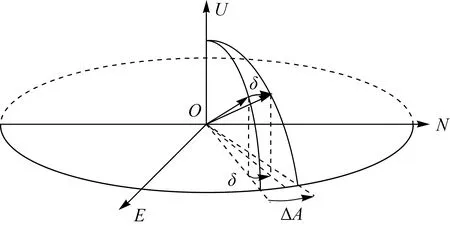
图3 天线水平准直差对方位角的影响Fig.3 The effect on the azimuth angle caused by telescope collimation error

2.2 指向改正模型推导

如图4所示，推导步骤为：

(1) 设初始状态，坐标系Oxyz与OENU重合，此时天线方位俯仰均为0，定义某点p位于天线指向上，距离参考点(原点O)为无量纲的单位矢量P。

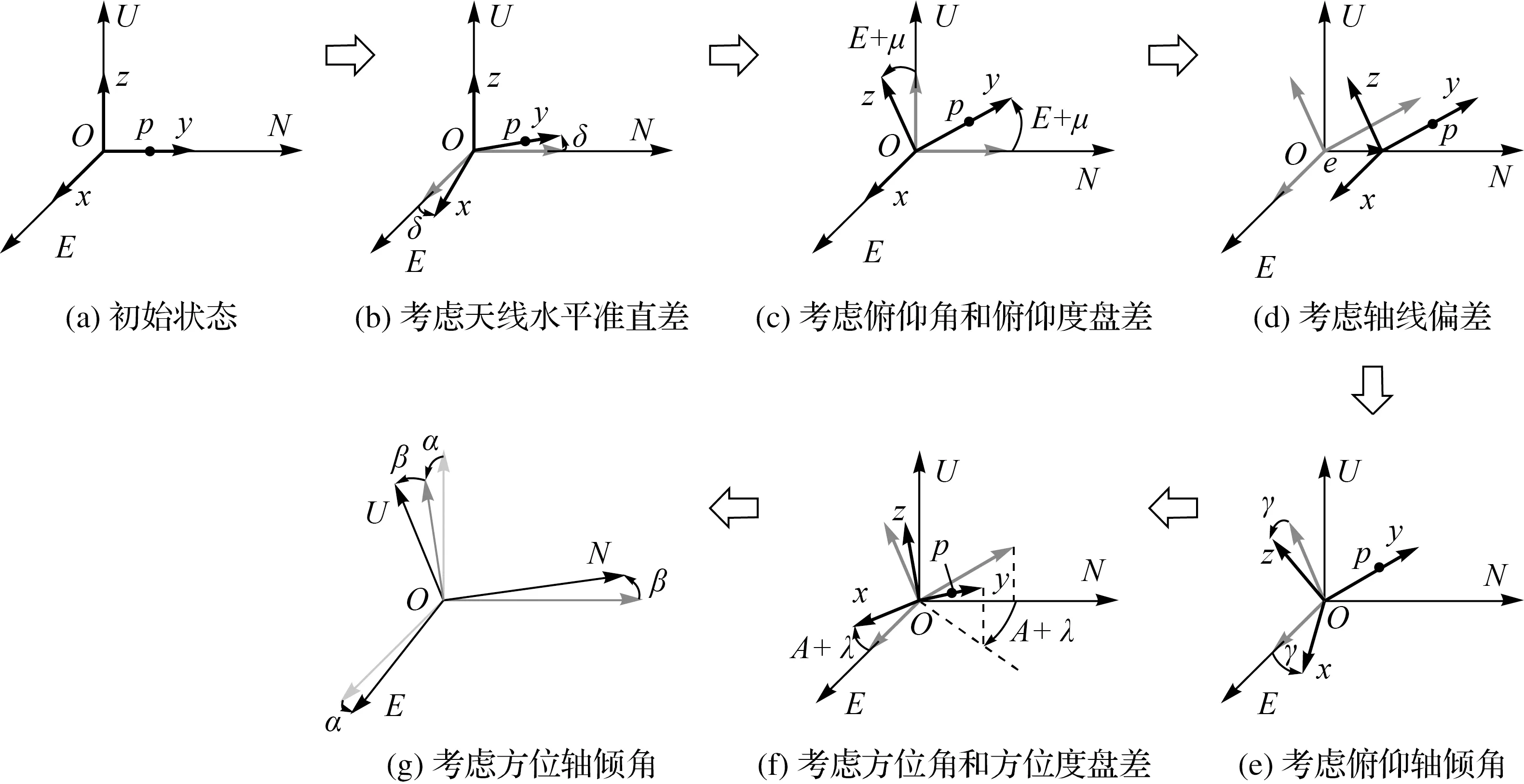
图4 天线轴系改正模型推导过程Fig.4 The derivation process of correction model of telescope axes

(2) 依次考虑天线准直差δ、俯仰角E、俯仰度盘差μ、轴线偏差e、俯仰轴倾角γ、方位角A、方位度盘差λ，方位轴倾角α和β，p点在OENU中考虑了轴系误差的位置P′与P的关系如式(1)所示

P′=R1(β)R2(α)R3(-A-λ)R2(γ)

[e+R1(E+μ)R3(δ)P]

(1)

设此时通过扫描法所测定的射电目标的真实位置为Ao与Eo，则P′在OA′RE′坐标系中的位置P″可由式(2)计算得到

P″=S1(Eo)S3(-Ao)P′

(2)

如上所述，p点与固定于天线指向上相对天线某一指向下在OA′RE′系中的理论位置仍可用P表示，由此得到天线轴系误差指向改正模型的完全表达式C，见式(3)

C=P″-P

(3)

令Ao=A，Eo=E，且对轴线倾角进行小角近似简化，令α、β等小角参数的正弦量为对应小角，余弦量为1。为方便描述系数矩阵，式(3)可拆解为式(4)

(4)

2.3 天线指向改正模型

式(4)为天线轴系误差改正模型的完全表达式，指向模型的轴系影响系数矩阵即CA和CE。为确保轴系误差模型精度达到1″以内，可舍去CA和CE中二次及以上的项，则天线指向轴系误差改正模型见式(5)

(5)

该模型包括了常用的9项天线指向改正模型[26]中有关轴系误差的项，也是22项天线指向模型[27]轴系误差的主项。

2.4 天线归心测量模型

天线归心测量模型构建了天线参考点位置Prp，天线轴系误差α′、β′、γ及e，以及本地观测靶标点理论位置Pcalc之间的关系。文献[28]给出的Lösler归心模型，如式(6)所示，该式坐标系与正负角度定义分别与上文一致

Pcalc=Prp+R1(β′)·R2(α′)·R3(A+OA)·

R2(γ)·R1(E+OE)·(Ptel+e)

(6)

式中，OA和OE分别为起始方位角和起始俯仰角，OA不仅包含了2.1.3节中λ，也包含了本地坐标系与OENU北方向之间的方位差；OE则包含了2.1.3节中的μ以及靶标位置与指向位置的俯仰角之差；2.1.3节中提到的天线准直差δ则被靶标位置矢量Ptel吸收；A、E、γ及e的定义与2.1.3节中的定义完全相同；由于归心测量是基于本地高程基准开展的，因此归心测量模型中的站心坐标系OENU3轴中的“上”指过参考点垂线的反方向，即α′和β′表示的是天线方位轴相对本地垂线的倾角。

通过对VLBI站开展归心测量，观测与VLBI天线随动的靶标轨迹，结合靶标点理论位置和实测位置，构建及解算误差方程，即可确定参考点及式(6)中各轴系参数的值。

2.5 垂线偏差求解

由上文可知，天线指向模型中的α与β是天线方位轴相对于法线的倾角，而天线归心测量模型中的α′和β′是天线方位轴相对于垂线的夹角。一般情况下，天线方位轴指向是不变的，因此可由式(7)求得VLBI测站本地垂线偏差

(7)

式中，η⊙与ξ⊙分别表示西东向与北南向的垂线偏差，本文定义垂线法线均指向天顶方向，则垂线偏差也标注天顶方向。

3 试验与结果

3.1 试验过程

2011年7月至2011年8月，对乌鲁木齐南山站25 m VLBI天线开展了归心测量与天线指向测量。本次归心测量，围绕VLBI天线共布设了连同GNSS基准站(GUAO)在内的共6个基墩组成的本地控制网，如图5所示。控制网的GNSS坐标结果由超过1周的同步环观测数据解算得到。天线归心测量过程及参数解算细节可参考文献[29—30]。天线指向修正观测作为天线的常规维护任务，一般几月进行一次。南山站采用22项天线指向修正模型，其中与轴系误差相关的7项修正项与本文定义相同，模型拟后指向精度约5″～10″[31]。南山25 m天线已于2014年重建，2011年的天线状态已不可追溯，此处取7″作为其拟后残差。对于式(5)中方位改正模型右侧5项，以及俯仰改正模型右侧4项，令各项对天线指向的贡献相同，则天线指向改正模型中的轴线拟合系数的精度为3″～4″。

2020年5月，采用AT330型数字天顶摄影定位系统(天顶筒)，依据GJB 149A—2013《军用天文测量规范》对乌鲁木齐南山站开展了垂线偏差测定。结合观测期间乌鲁木齐南山站气象条件与地面硬化范围限制，共选取了5个DOV观测点，如图5中“△”所示，具体测定结果见表2。南山站2020年DOV值与2011年相比可能存在长期性变化，对于京滇地区重复测量结果表明，DOV每年有0.001″～0.004″的偏移[32]，具体因地而异，但9年的DOV差别仍在实测精度范围内。

图5 南山并置站本地连接控制网(▲)与垂线偏差观测点(△)Fig.5 Local control network (▲) and DOV surveying points (△) in NANSHAN co-located station

表2 南山站DOV实测值

3.2 轴系误差间的一致性

表3为归心测量与天线指向模型中所解算的各轴系参数对照表。指向测量和归心测量分别基于本地法线和本地垂线，其所解算方位轴倾角参数间存在不一致，这种不一致即DOV；22项天线指向修正模型给出的e为151.76″，考虑弧度为无量纲单位，将“m”作为上节中e的单位，则e等于0.7″，e的符合度为1～2 mm，类似的可将其形式精度4″换算到长度单位；天线俯仰轴参数γ符合得很好。

3.3 垂线偏差结果

采用其他3种方法对本文反演的DOV结果进行验证，包括易于开展的地形积分方法、重力场模型法以及最为可信的天顶筒实测法。各种方法相互比较，同时也可用以分析不同模型和方法间的一致性。天顶筒实测法在3.1节中已进行介绍，本文取与VLBI天线站址最为接近的D1点作为该区域DOV的实测值；重力模型法则利用我国2000中国重力场与似大地水准面模型(CGGM2000)[17]计算出南山站VLBI天线处的DOV值。下面对地形积分法进行详细说明。

表3 归心测量与天线指向模型中的轴系参数对照

相关计算参考紫金山重力异常对时间测定影响的计算经验[5]，本文称其为地形积分模型。假设天线周边地壳中物质分布均匀，对天线周边东西和南北区域分块并做地形填补，计算东西向和南北向物质分布差异，从而确定测站周边物质分布引起的重力异常。如图6所示，调取南山站周边30 km内的地形，并以南山站参考点为中心，分为东西侧和南北侧开展计算，具体计算过程如下。

首先标记参考点对应两侧(如西侧和东侧)土方填挖量相同时各自的参考高程HW和HE，那么参考点两侧中的一侧(西侧或东侧)将形成半圆台土方形状，利用式(8)计算其相对天线参考点处的东西侧引力异常ΔgWE。图6中，计算东西重力异常，先将Ⅲ和Ⅳ区域作为整体，填成半圆台状，再将Ⅰ和Ⅱ区域作为整体，填成半圆台状，两个半圆台高程差出的部分，即为东西侧物质之差。同理可得南北重力异常

(8)

式中，G为引力常数；ρ为岩土密度；H0为参考点处的高程；R为积分半径，取30 km。南山站周边山体沟壑纵横，采用30 km的积分范围可增加可信度，如果进一步扩大半径，积分区域会抵达天山北侧主峰，此时将不得不考虑山体负载均衡，因此本文以30 km为限。θ0和θ1分别为圆面角度积分下上限，HB和HU分别为土方填平后所形成圆台高程的下上限。利用不同的半圆台土方计算两个方向上的Δg，分别为西东向引力异常ΔgWE和南北向引力异常ΔgNS，这里还需扣除计算土方时的四分之一重叠半圆台土方Δgo，这部分土方对西东和南北向的重力影响相同。那么，由引力异常计算垂线偏差的计算式为式(9)。3个Δg的积分限的取值见表4，其中各填平半圆台上下高程值由数字高程模型软件Local SpaceViewer计算得到。

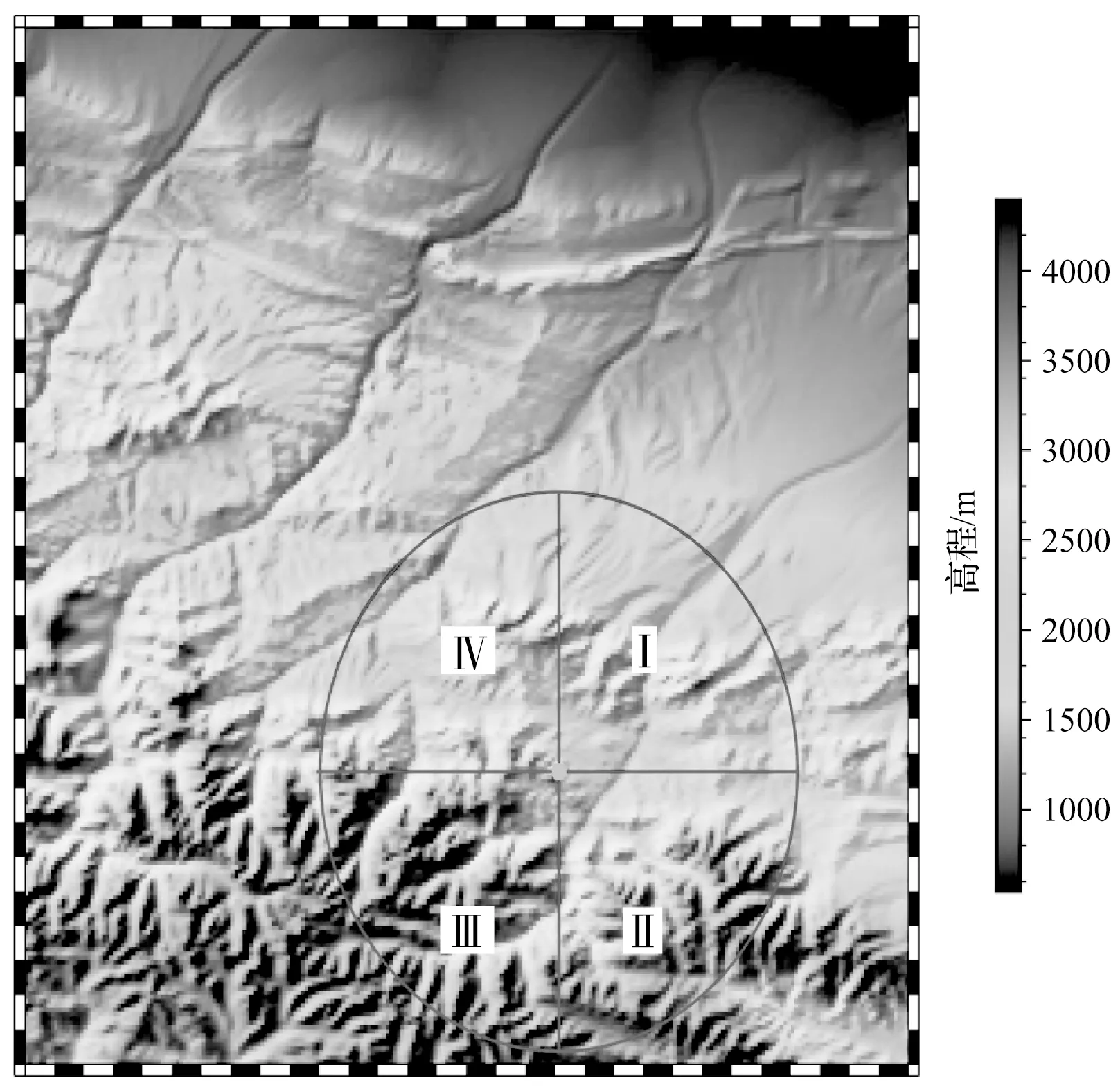
图6 南山周边地形及地形积分范围Fig.6 Topography and topography integral range around Nanshan

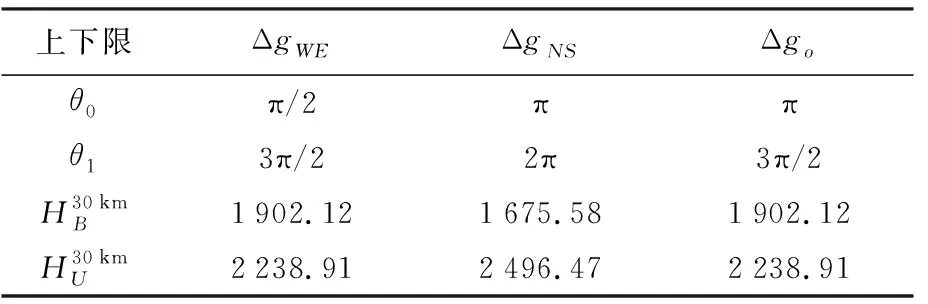
表4 不同Δg积分上下限取值

(9)

式中，φ和H0分别为测站纬度与大地高。相对于本地法线，垂线偏差u可以有两个方向，一个指向地心，一个指向天顶，文中分别用u⊗和u⊙表示，其分量表示方法也类似。采用VLBI天线轴线信息反演法、地形积分法、重力模型法以及天顶筒实测法所计算的DOV结果见表5。

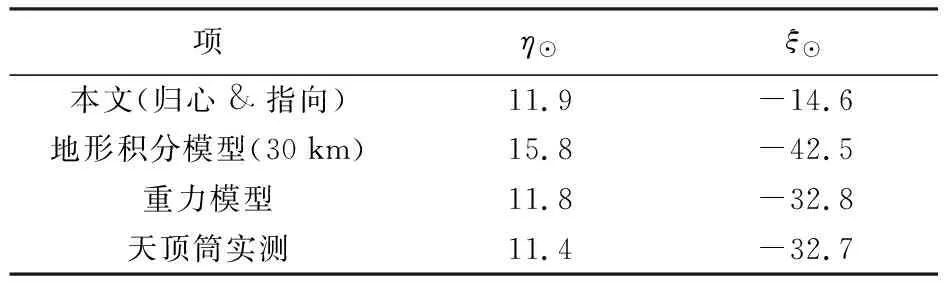
表5 垂线偏差值符合

由表5可知：①4种方法均可求取VLBI测站DOV，所求DOV分量的方向均一致，表5中DOV方向分别定义为东向和南向；②天顶筒在VLBI站点的DOV实测精度分别为0.047 7″(子午方向)和0.046 6″(卯酉方向)，重力模型精度约1″，两者符合度均在各自观测或标称精度范围内；③由于未考虑地底物质分布，地形积分模型所测DOV值在量级上相较实测值偏大；④用本文方法确定的DOV形式精度约5″，在卯酉方向上与实测值符合很好，在子午方向上存在着～18″的不符。这是由于天线指向校正测量时射电源在测站天区南北分布不均匀引起的。

3.4 讨 论

本文测定DOV的原理可概括为：通过基于本地水准面开展的归心测量确定天线方位轴相对垂线的倾角，再通过同一时期的天线指向测量确定天线方位轴相对于法线的倾角，两者之差即为测站垂线偏差。该值严格定义于天线参考点处，由指向测量和归心测量结果推出，无须另行开展天文大地观测。

VLBI归心测量控制网大小一般在方圆约200 m范围内(本例控制网中最长基线约为160 m)，控制网内的垂线方向具有一致性是本文方法开展的前提，即天线参考点处的垂线方向应能够代表整个本地归心测量控制网的垂线方向。归心测量中的水准是采用本方法开展VLBI站DOV测量的基础。

作为VLBI测站的常规测量标校手段，天线指向测量周期为几个月；而VGOS测量规范中规定，天线归心测量(本地连接测量)开展周期应为2.5 a。对于同期开展的归心测量与天线指向测量见表3，俯仰轴倾角以及轴线偏差参数间有着很好的符合度。

本文计算的DOV测量形式精度约为5″，DOV卯酉分量与实测值符合得较好，但在子午分量上两者差别达到了18″。其原因是天线在开展指向测量时，所观测射电源相对本地天区在东西方向上分布近乎对称，而在南北方向上分布不均匀。因南山站2011年天线指向测量状态已不可追溯，此处以上海天马VLBI全球观测系统(VGOS)站某次指向校准时所观测校准源的天区分布为例。观测校准源共5颗，如图7所示，这些源东西分布近乎对称而南北分布极不均匀，这导致了该天线方位轴倾角在子午分量上测定精度较差。类似情况，传统VLBI天线指向改正模型建立时，并不会太多关注参数的物理意义，且β值的多解性并不会影响天线指向模型的建立(并不会引起误差方程的奇异)，这使得DOV子午分量的测定出现较大的不确定性。后期将对天线指向修正观测纲要等开展优化设计，从而可以高精度测定β值。

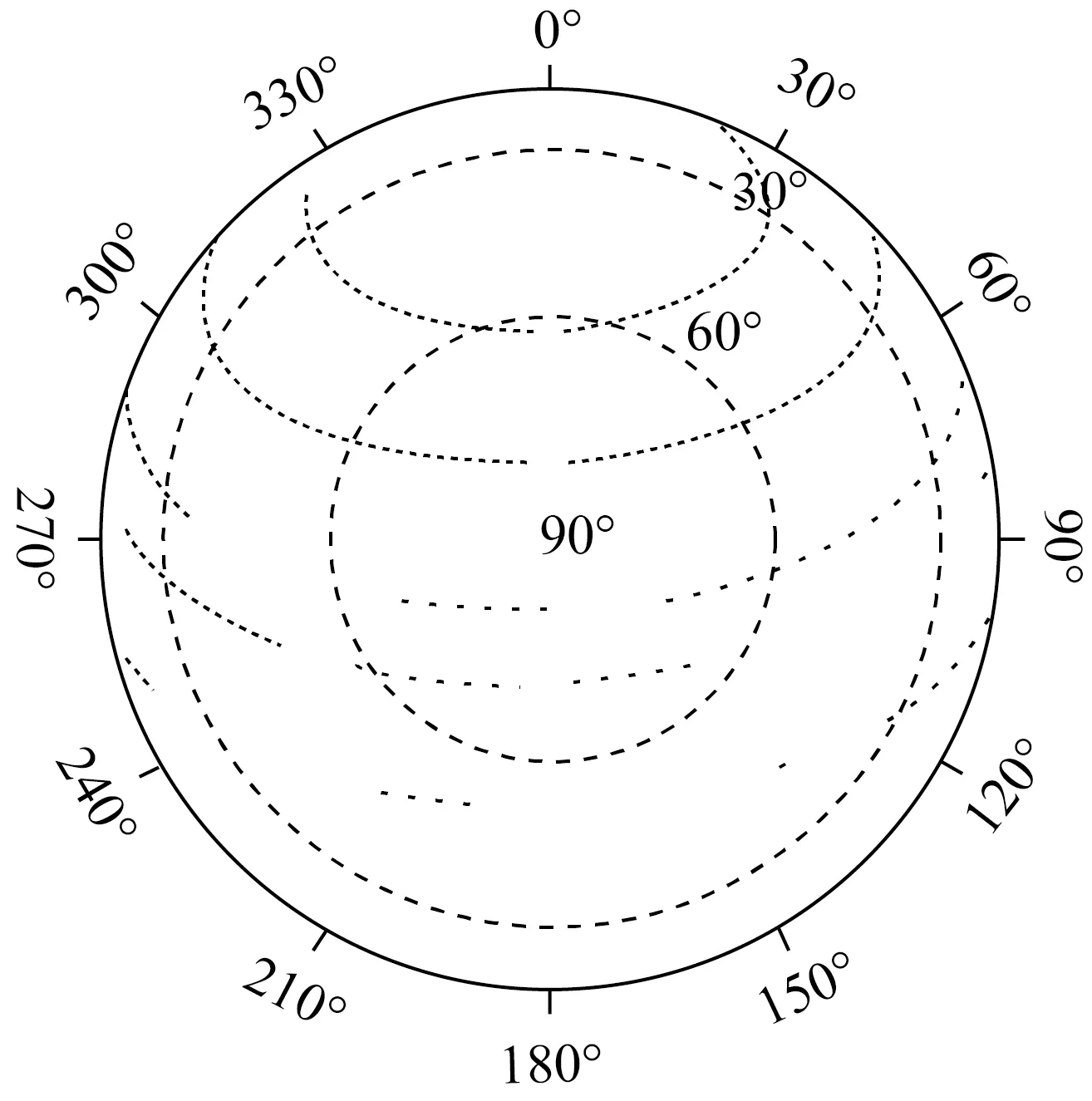
图7 某次天马VGOS指向修正所用的射电源分布(天顶俯视图)Fig.7 The case of observed radio source distribution used for the pointing calibration of the TIANMA VGOS(viewed from zenith)

4 结 论

本文通过构建统一的天线指向改正模型与归心测量模型，建立了VLBI天线指向改正测量、归心测量以及站点DOV测定三者间的联系，并基于南山站天线指向改正和归心测量实测数据，实现了站点垂线偏差的初步测定。结果表明，采用该方法所测得的站点DOV，在量级和方向上与实测值以及DOV模型值表现一致。因天线指向修正观测所采用的射电源南北分布不均匀，所测DOV在子午分量数值上存在一定偏差，然而所测DOV在卯酉分量上与天顶筒实测值的一致性可达0.2″。后续工作中，将针对天线指向修正观测与归心测量方案分别开展射电源天区覆盖与靶标点覆盖的专项优化，预计DOV测定精度可提高约1″。

通过引入归心测量中的水准信息，VLBI天线将不再对重力方向变化“不敏感”。考虑到天线指向测量与归心测量是VLBI天线的常规维护手段，采用该方法不仅可实现射电天线站点DOV的“零成本”监测，而且有望实现VLBI测站的DOV常规监测。