测站分布对GPS解算ERP的影响分析

黄春桃，刘学习，蔡顺中，魏二虎

(1.中山市中鑫测绘工程有限公司，广东 中山 528451； 2.武汉大学测绘学院，湖北 武汉 430079)

1 引 言

地球定向参数(EOP)包括地球自转参数(ERP)，岁差和章动。其中地球自转参数是指极移(polar motion)和日长变化(LOD)。地球是一个非常复杂的系统，地球自转参数与地球上物质迁移和运动，地外天体引力，固体地球负载形变有着很强的相关性。另外，地球自转参数还是地球参考系到天球参考系转换的重要的参数[1]；也在飞行器精密定轨和自主导航等方面发挥着重要的作用[2]。

现在确定高精度地球自转参数的手段主要有VLBI、SLR、LLR、GPS等方法[3]。其中利用GPS测定地球自转参数已成为当今重要的手段之一。因为GPS数据量充足，并且能够得到高时间分辨率和长时间跨度的地球自转参数，且相对于上述几种手段来说价格低廉。但是在利用GPS解算地球自转参数的过程中，测站数目、观测弧段和测站分布会对解算的效率和解算得到的精度产生很大的影响。文献[4，5]中，曾经研究了测站数目和观测弧段对解算精度的影响分析。但是很少有资料涉及测站分布对GPS解算地球自转参数的影响分析。基于此，本文旨在研究测站分布对解算地球自转参数的影响分析。同时本文也希望能够通过本文的研究对利用北斗亚太区域的测站解算地球自转参数提供参考。

2 GPS解算ERP的原理

(1)

(2)

P、N、R、W分别为岁差、章动、地球自转和极移转换矩阵。极移参数(xp，yp)和日长变化参数LOD (为方便推导用地球旋转角θ表示)分别包含在矩阵W和R中，△ε、△ψ为岁差章动参数，将式(1)线性化可得：

(3)

(4)

假设有m个测站对n颗卫星进行观测，将偏导数代入观测方程可得：

(5)

其中：

根据最小二乘准则估计ERP参数并进行精度评定：

(6)

(7)

式中(n-t)、V、σ0和Q分别为自由度、残差、单位权中误差和协因数阵。

3 数据处理与分析

在探究测站分布对GPS解算ERP的影响分析时，首先应当保证有足够的观测弧段和测站数目。随着测站数目和观测弧段的增加，计算时间呈指数增加，而解算的精度提高并不明显，因此根据以前的研究成果，当测站数目达到40个以上时，可以满足解算的要求。所以，本文选择40个测站，24 h的观测弧段采用如下三种方案来解算ERP参数[10]。另外，在选取IGS测站时，主要考虑以下几个因素：①尽可能多地选取ITRF2008框架下的GPS观测站；②测站坐标中误差在 1 mm以下；③并且速度场中误差小于 0.3 mm/a[11]。

方案一：40个均匀分布在全球的IGS测站，如图1所示。

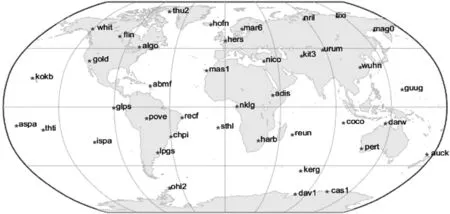
图1 40个均匀分布在全球的IGS测站

方案二：40个均匀分布在东半球的IGS测站，如图2所示。

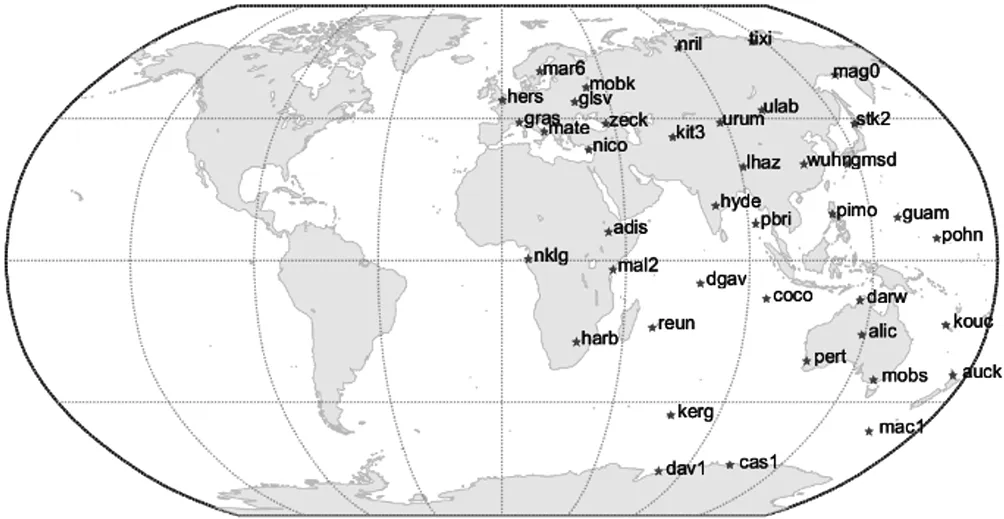
图2 40个均匀分布在东半球的IGS测站

方案三：40个均匀分布在东北半球的IGS测站，如图3所示。

图3 40个均匀分布在东北半球的测站

本文采用2014年3月11日～4月30日即年积日为70～120共51天的数据(个别参考站可能没有当天的数据，此时采用其周围的参考站数据来代替)并采用bernese5.0软件进行数据处理，解算每天UTC为12：00的ERP参数。采用上述三种方案分别解算ERP，并将解算所得到的结果与IGS发布的ERP值作差，其差值的绝对值如图4～图6所示[12，13]。其中W表示测站均匀分布在全球，E表示测站均匀分布在东半球，NE表示测站均匀分布在东北半球。

图4 极移xp解算结果与IGS发布结果差值的绝对值

图5 极移yp解算结果与IGS发布结果差值的绝对值

图6 极移UT1-UTC解算结果与IGS发布结果差值的绝对值

从图4可以看出：对于极移xp，测站分布在全球比测站分布在东半球精度和稳定性有显著提高，测站分布在东半球也比测站分布在东北半球精度有所提高。从图5可以看出：对于极移yp测站分布在全球比测站分布在东半球精度和稳定性有所提高，但是测站分布在东半球却比测站分布在东北半球略有下降。这可能是由于测站分布在东半球并不比测站分布在东北半球的空间结构好多少有关，具体原因还有待探讨。从图6中可以看出测站分布对UT1-UTC的影响很小，测站均匀分布在全球并不比测站均匀分布在东半球精度有显著提高，同样测站均匀分布在东半球只比测站均匀分布在东北半球的精度略有提高，这一点可以从利用这三种方案所得到的ERP的均方根误差中得到印证。这是由于日长变化对测站分布不敏感所致。如表1所示。总的来说测站分布在全球所得到的ERP的精度最高。因此，笔者建议在计算地球自转参数时，应尽量选择均匀分布在全球的测站。

不同测站分布51天的ERP均方根值 表1

4 结 语

本文详细研究了测站分布对利用GPS解算ERP精度的影响。利用全球IGS测站，设计了三种不同方案来探究测站分布对GPS解算ERP的影响，以期能够在现有的测站分布的情况下，选择最佳的测站分布方案。并且能够为利用北斗区域网解算ERP参数提供参考。

通过本文的实验证明，在这三种方案中，测站分布情况对极移xp的影响较大，当测站均匀分布在全球时，比测站均匀分布在东半球和东北半球的精度和稳定性都要高；测站分布在全球时对极移yp解算的精度最高。测站分布对UT1-UTC的影响相对较小，三种方案得到的结果相差不大。但是总体来说测站均匀分布在全球的时候，得到的结果的稳定性和精度和IGS发布的值相比，都能够达到要求。

本文虽然分析了三种不同方案对GPS解算ERP的影响，但是没有能够用数学的方法来描述测站的网型和最终解算精度的影响关系。这将是下一步研究的重点工作。

[1] Wei E，Yan W，Jin S，et al. Improvement of Earth orientation parameters estimate with Chang’E-1 △VLBI observations[J]. Journal of Geodynamics，2013，72：46～52.

[2] Wei E，Jin S，Zhang Q，et al. Autonomous navigation of Mars probe using X-ray pulsars：Modeling and results[J]. Advances in Space Research，2013，51(5)：849～857.

[3] 李征航. 空间大地测量学[M]. 武汉大学出版社，2010.

[4] 朱圣源，赵铭. 多种技术测定地球自转参数综合解的简化算法[J]. 中国科学院上海天文台年刊，1986(00).

[5] 魏二虎，李广文，畅柳等. 利用GPS观测数据研究高频地球自转参数[J]. 武汉大学学报·信息科学版， 2013(07)：818～821.

[6] Xu G C. GPS：theory，algorithms，and applications[M]. Springer-Verlag Berlin Heidelberg，2007.

[7] Dach，R.，Hugentobler，U.，Fridez，P.，&Meindl，M. (2007). Bernese GPS software version 5.0.Astronomical Institute，University of Bern，640.

[8] Yang ZH K，Yang X H，Li ZH G，et al. Estimation of Earth Rotation Parameters by GPS observations[J]. Journal of Time and Frequency，2010，33(1)：69～76. (Chinese).

[9] Wang Q，Dang Y，Xu T. The Method of Earth Rotation Parameter Determination Using GNSS Observations and Precision Analysis[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings. Springer Berlin Heidelberg，2013：247～256.

[10] 魏二虎，刘学习，孙浪浪等. 测站数目和观测弧段对GPS解算地球自转参数的影响分析[J]. 大地测量与地球动力学，2017，37(2)：187～191.

[11] 魏二虎，万丽华，金双根等. 联合GNSS和SLR观测对地球自转参数的解算与分析[J]. 武汉大学学报：信息科学版，2014，39(5)：581～585.

[12] Herring，Thomas A.，and Danan Dong. “Measurement of diurnal and semidiurnal rotational variations and tidal parameters of Earth.” Journal of Geophysical Research：Solid Earth (1978-2012) 99.B9 (1994)：18051～18071.

[13] Haas，Rüdiger，and Johann Wünsch. “Sub-diurnal earth rotation variations from the VLBI CONT02 campaign.” Journal of Geodynamics 41.1 (2006)：94～99.