大范围地表沉降时序深度学习预测法

2021-04-01刘青豪张永红吴宏安康永辉魏钜杰

测绘学报 2021年3期

刘青豪，张永红，邓敏，吴宏安，康永辉，魏钜杰

1. 中南大学地球科学与信息物理学院，湖南长沙 410083； 2. 中国测绘科学研究院，北京 100830

地面沉降是指在自然和人为因素作用下，由于地壳表层土体压缩而导致区域性地面标高降低的一种环境现象，又称地面下沉或地沉[1]。由于城市化的快速发展，人类对自然资源的需求不断增加，煤、石油、天然气、地下水等自然资源的不断开采使得地面沉降问题变得越发严重，地面沉降问题已成为世界性的地质问题。因此，开展大范围地面沉降预测预报分析，对国土空间规划、防灾减灾等具有重要的研究价值和现实意义。

在大范围地表沉降预测方面,目前的研究并不丰富。文献检索发现，已有的地表沉降预测方法主要可归纳为三大类：基于物理机制的方法、基于数理统计的方法以及基于机器学习的方法。基于物理机制的方法从沉降内部的物理演化过程出发，通过实地检测和试验的方式获取包含岩性特征、水文特征在内的一系列复杂的物理参数，进而对地面沉降进行模拟与预测[2-5]，常见的模型包括采矿沉降模型、地铁沉降模型、地下水耦合模型等。然而，由于各种参数的存在，很多情况下需要对该类方法做出严格的假设才能应用，而这些假设有时可能会失效，如，由于地表沉降现象存在复杂的成因而难以确定的趋势性及周期性等。基于数理统计的方法通过分析大量历史监测数据的内在关系及发展规律，采用包含回归分析、灰色预测等在内的数学模型来实现地面沉降的模拟。然而，由于未考虑地下岩土介质的本构关系，该类方法通常难以推广。采用此类方法的研究主要有文献[5—7]，能否正确选择参数模型在很大程度上决定了该类方法预测结果的准确率。基于机器学习的方法是在计算机的辅助下进行沉降特征的学习，不受研究区域地质及水文等复杂物理参数的限制。其原理中的回归思想与时间序列预测有着紧密的关系[8]，经典的支持向量回归、人工神经网络、贝叶斯网络、小波分析等方法在时间序列预测方面均取得了不错的效果[9-12]。该类方法依赖历史数据的驱动。现有的机器学习方法在地表沉降预测方面尚存在两个困难：首先，高维的数据不仅影响了机器学习的速度，而且可能包含错误的噪声信息，如何从高维数据中选择关键的特征进行学习直接影响着沉降预测的精度；其次，由人类活动导致的地下水位升降等相关数据与沉降观测点的粒度难以匹配，生硬的插值必然降低训练样本的质量。以上两个难题使得机器学习方法因特征选择困难或样本粒度的差异而难以得到较高的预测精度，并且模型的泛化能力较弱，难以对存在地质条件差异的区域进行沉降预测。因此，如何利用历史数据建立有效的预测模型，对未来地表沉降进行模拟，是一项十分重要的工作。

综合上述分析可以发现：在大范围地表沉降预测中，现有沉降预测方法因模型参数难以获取或相关数据的缺乏而难以得到可靠的预测结果[2-12]，通过分段线性逼近来实现沉降时间序列的非线性拟合，在本质上忽略了时间序列中的非线性关联[12]。本文提出一种基于深度学习的地表沉降时序预测方法，并通过沧州地区2012—2016年地表沉降InSAR监测数据进行建模验证。结果表明，该方法具有很好的预测效果。

1 基于LSTM的地表沉降时序预测方法

近年来，深度学习作为一种新的机器学习方法受到很多行业的高度关注[13-16]。其中，循环神经网络(recurrent neural network,RNN)能够使得网络当前的运行不仅跟当前的输入数据有关，并且可以与之前的数据建立联系。然而，每个隐含细胞单元计算的最后都要经过一个非线性函数，使其输出为[0,1]之间的结果，这使得十几次运算后数值会衰减到很小而无法记忆较远位置的数据。此外，梯度爆炸也是普通RNN模型容易面临的困难。为解决这两种问题，文献[16—17]提出了长短期记忆(long short-term memory,LSTM)网络模型。该模型是一种特殊的RNN，通过在隐藏层增加门机制来控制信息的流失，再经过反向传播过程的动态调整，使得网络可以学习长距离的时间序列数据。本文正是利用了LSTM模型的这一优点，提出基于LSTM模型的大范围地表沉降时序预测方法。

1.1 长短期记忆网络模型

隐藏层是整个LSTM网络的核心，由多个LSTM细胞单元组成，细胞单元的结构如图1所示。

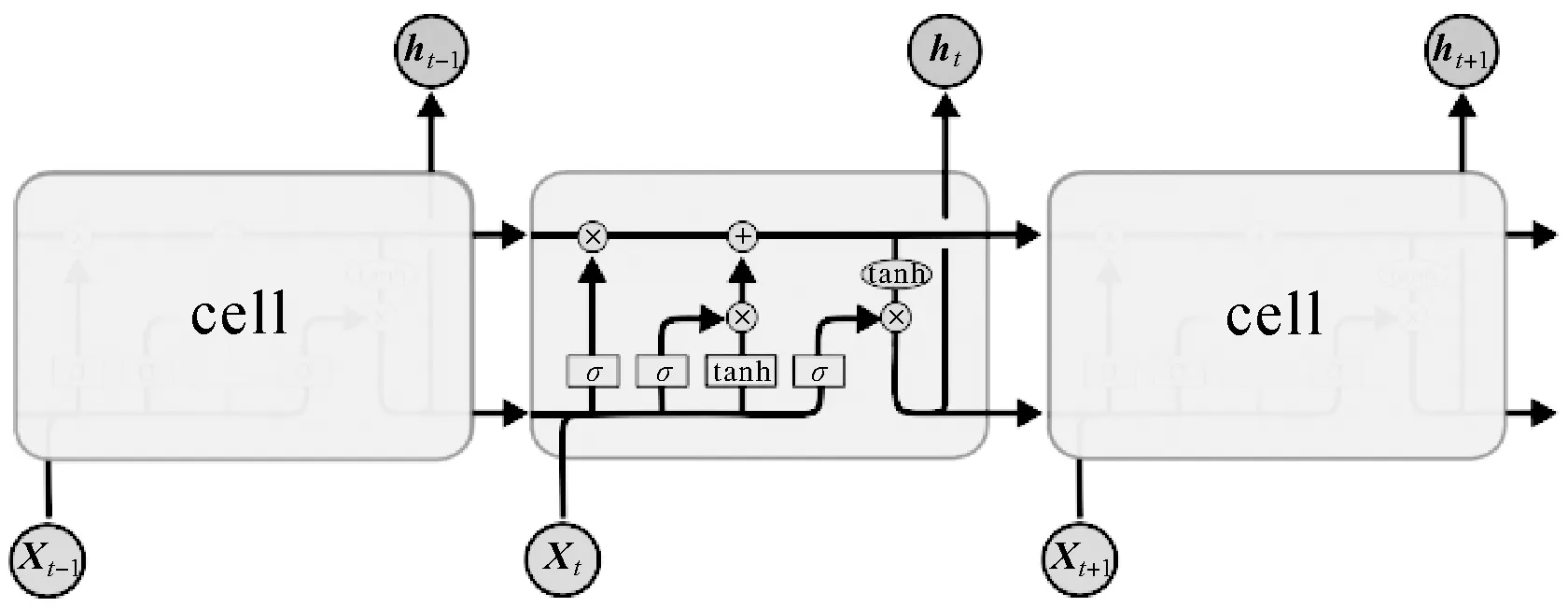
图1 LSTM隐藏层细胞结构Fig.1 Cell structure of LSTM hidden layer

图1中共显示了一层隐藏层中的3个细胞单元。xt表示样本时间序列中第t时刻的输入，ht表示相应细胞单元的隐含状态输出。每个细胞单元中依次进行数据输入、信息遗忘、细胞状态更新以及隐含状态输出，其前向计算方法可以表示为

it=σ(Wxixt+Whiht-1+Wcict-1+bi)

(1)

ft=σ(Wxfxt+Whfht-1+Wcfct-1+bf)

(2)

ct=ftct-1+ittanh(Wxcxt+Whcht-1+bc)

(3)

ot=σ(Wxoxt+Whoht-1+Wcoct+bo)

(4)

ht=ottanh(ct)

(5)

式中，i、f、c、o分别表示输入门、遗忘门、细胞状态、输出门；W和b分别为对应的权重系数矩阵和偏置项；σ和tanh分别为sigmoid和双曲正切激活函数。LSTM模型训练过程采用的是与经典的反向传播算法原理类似的BPTT算法[18]，主要包括4个步骤:①按照前向计算方法计算LSTM细胞的输出值，即式(5)；②反向计算每个LSTM细胞的误差项，包括按时间和网络层级两个反向传播方向；③根据相应的误差项，计算每个权重的梯度；④应用基于梯度的优化算法更新权重。

1.2 基于LSTM的地表沉降时序预测模型

基于前述LSTM预测原理，结合地表沉降中单变量短时序的数据特征，构建了基于LSTM的地表沉降时序预测模型。该模型的整体框架如图2所示，包括输入层、隐藏层、输出层、网络训练以及网络预测5个功能模块。输入层负责对原始地表沉降数据进行预处理以满足网络输入要求，隐藏层采用图2表示的LSTM细胞搭建循环神经网络，输出层提供预测结果，网络训练采用ADAM优化算法，网络预测采用迭代的方法逐点进行预测。

通过长短期记忆网络动态的调整，模型可以充分学习不同沉降时间序列中的非线性关联，进而可以捕获研究区域中的复杂沉降机理。该方法不仅可以降低预测过程对历时数据质量的要求，而且从本质上可以提高沉降预测精度与可解释性。

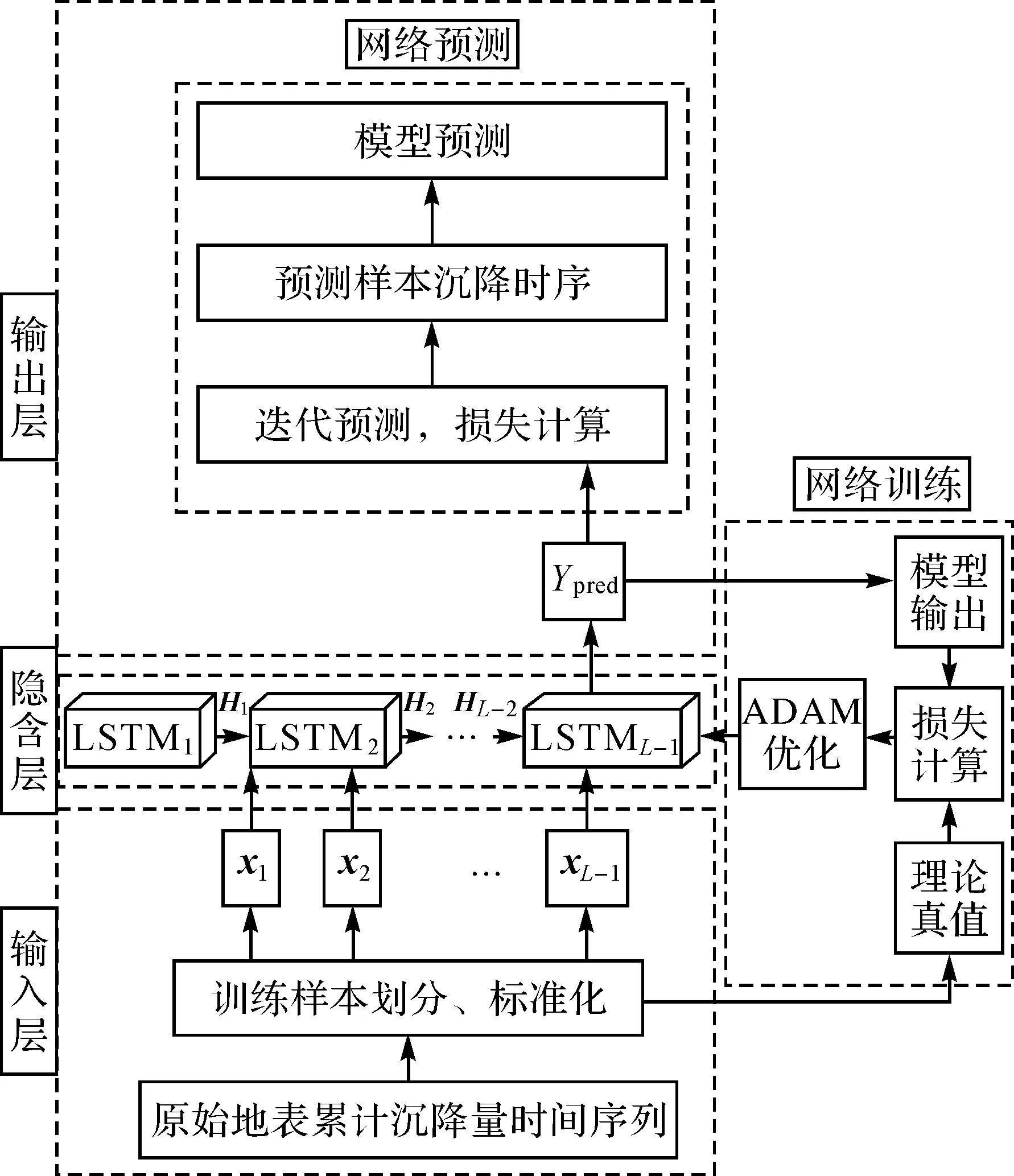
图2 基于LSTM的地表沉降时序预测框架Fig.2 Prediction framework of land subsidence time series based on LSTM

1.2.1 数据预处理

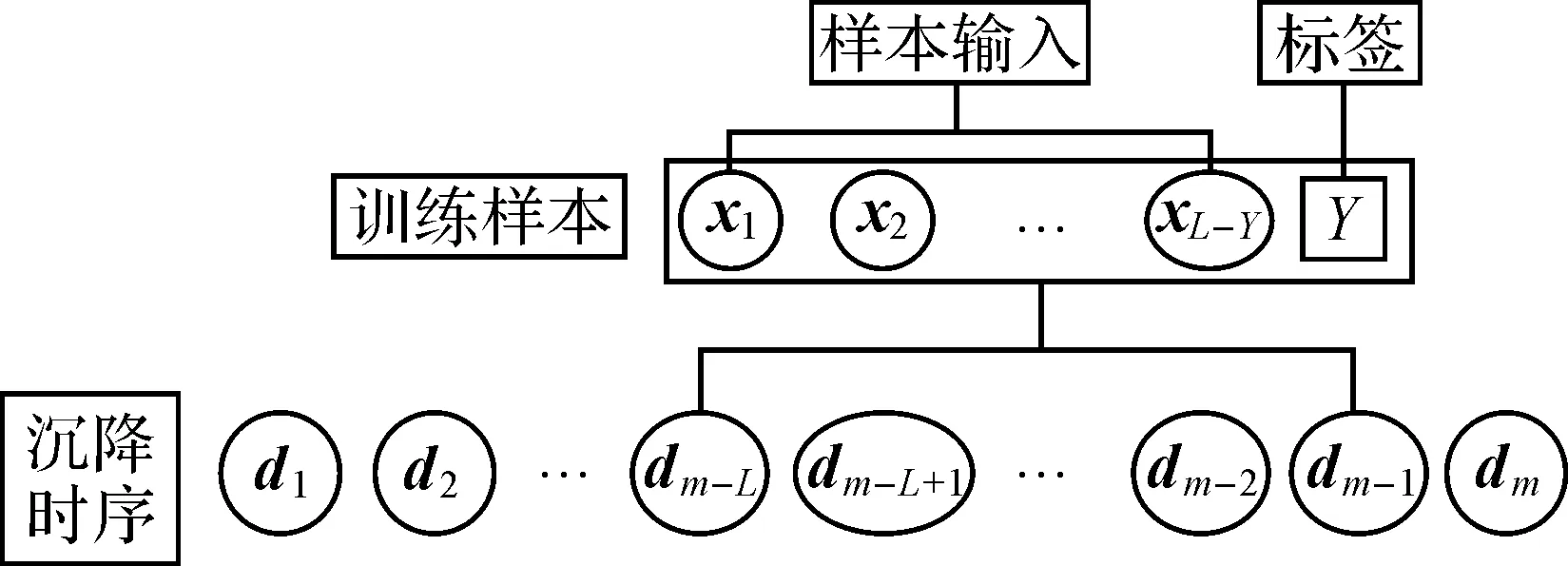
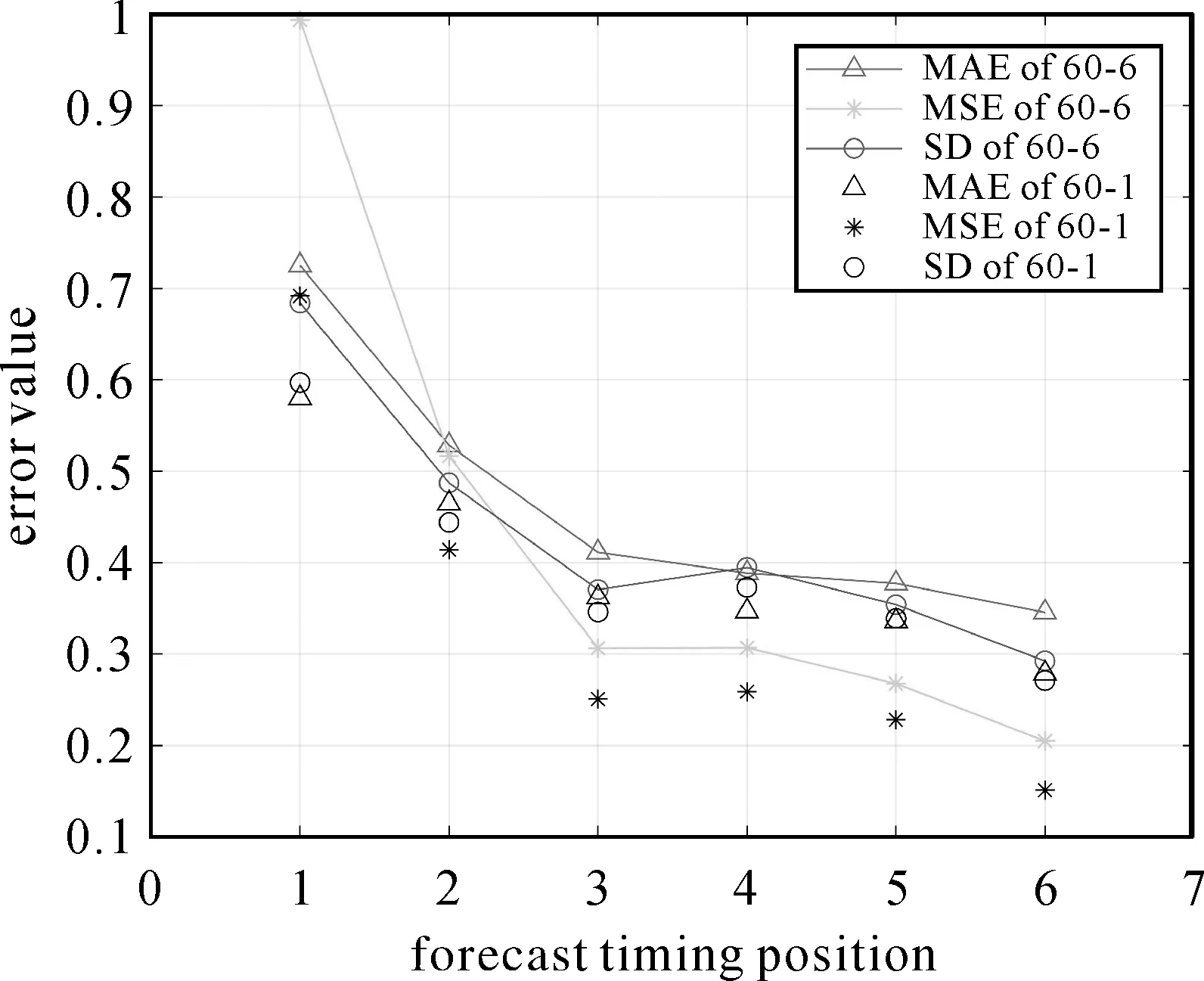
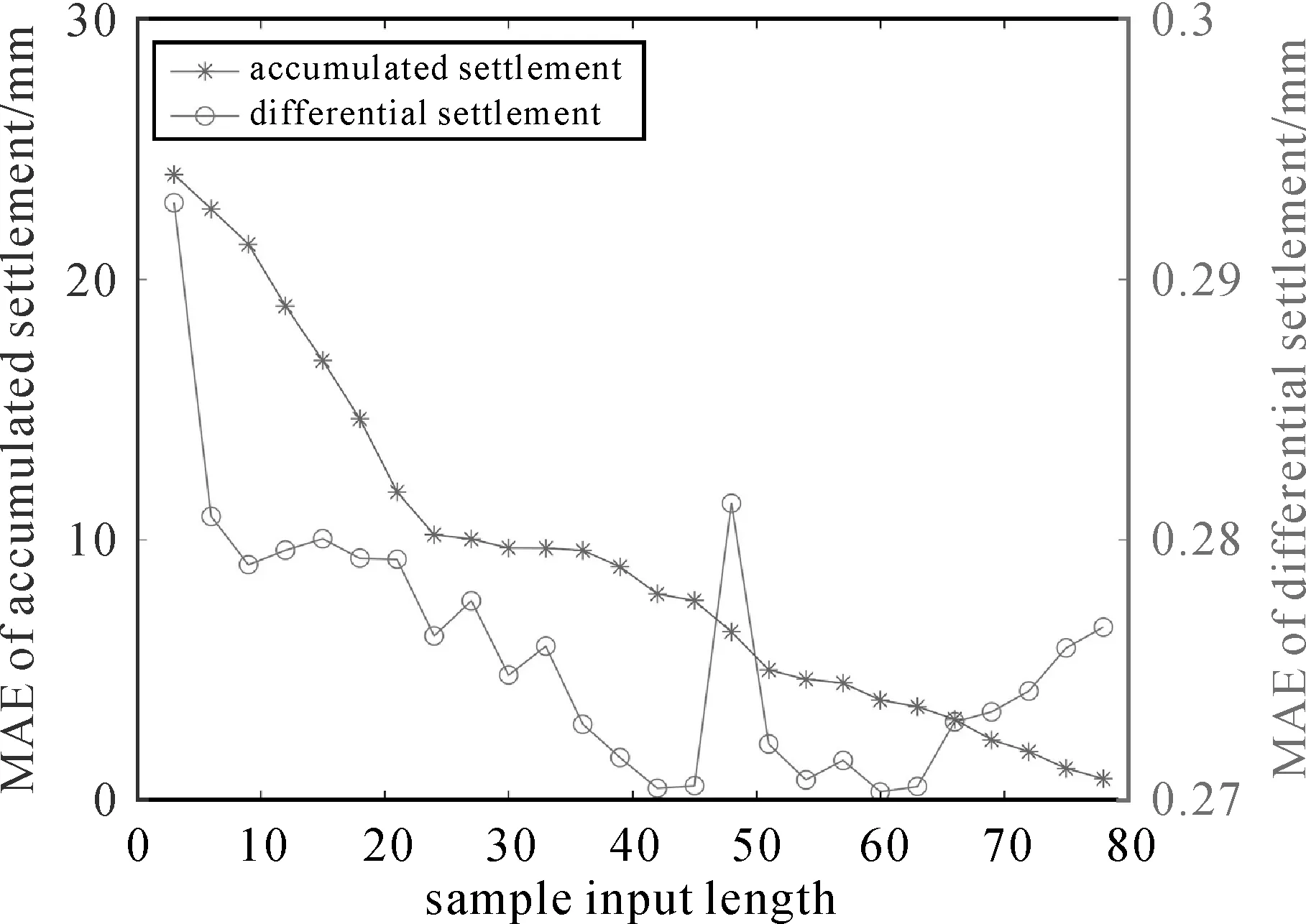
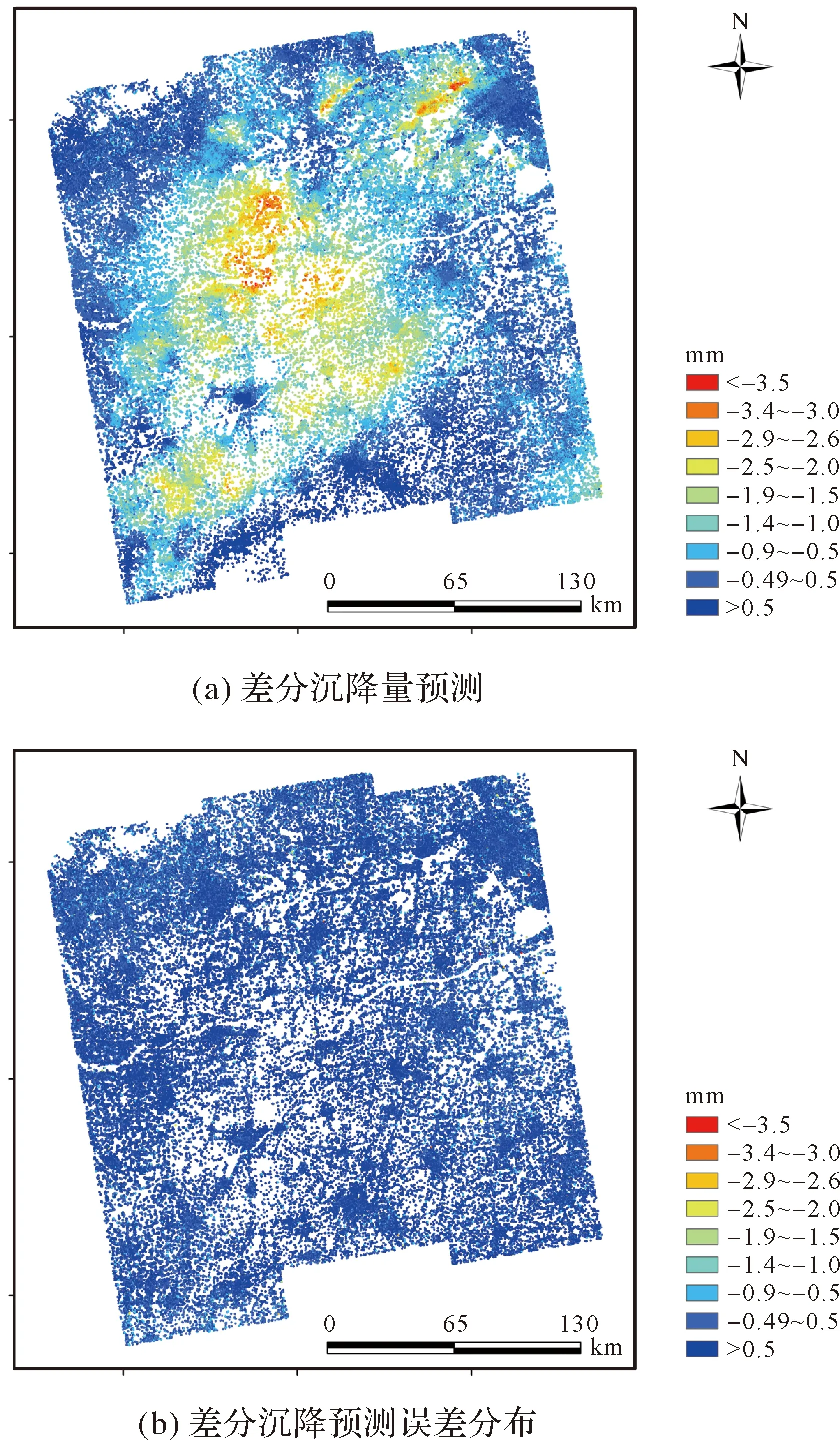
时间序列分析法是根据序列过去的变化趋势来预测未来的发展变化，因此事物的发展需具备一定的持续性[19]。为确定最优的序列长度，获取高质量的训练样本，对累计或差分沉降量时间序列(下称“沉降时序”)进行预处理。首先将每个观测点的沉降时序记为Dm={d1,d2,…,dm}，则每个沉降时序中可提取出一个长度为可控参数L的训练样本，记为Dtrain={dm-L,dm-L+1…,dm-1}，其中，样本的后Y个数值用作样本标签，前(L-Y)个数值用作样本输入，且满足约束条件2≤L

(6)

(7)

式中，m-L≤t≤m-1,t∈N。

图3 单个沉降时序中的样本划分Fig.3 Sample division in single settlement time series

1.2.2 网络训练

网络训练主要以隐藏层为研究对象。从图2可以看出，隐藏层包含(L-1)个依次连接的同构LSTM细胞单元，经过每个细胞单元的模型输出可以表示为

Ot=LSTMforward(Xt,Ht-1,ct-1)

(8)

(9)

本文选用文献[20]提出的适应性动量估计(adaptive moment estimation，ADAM)算法作为优化器。该算法融合了AdaGrad[21](adaptive gradient algorithm)和RMS Prop[22](root mean square Prop)算法的优势，能够对不同参数计算适应性学习率并且占用较少的存储资源。与其他随机优化方法相比，ADAM算法在实际应用中整体表现更优[20]。设定损失函数最小为优化目标，给定样本分割长度L、网络层数K、隐藏层节点数S、学习率l以及训练次数epochs，不断更新网络权重，进而得到训练好的预测模型。

在构建上述LSTM预测模型中，涉及众多网络参数，其中以样本划分长度L、网络层数K和每层LSTM隐藏层的特征数量S最为关键[17]。为了达到更好的预测效果，本文采用多层网格搜索的方法对这3个参数进行优选。以平均预测精度最高作为参数优选的依据，即预测样本的沉降量预测误差ε(Y,Ypred)最小，目标函数可以表示为

minε(Y,Ypred)=|Ypred-Y|

(10)

式中,stepL、stepK和stepS分别为对应参数的网格搜索步长；L、K和S这3个参数构成了一个三维搜索空间，可以通过多层网格搜索算法获取最优参数组合。搜索过程主要包括3层，从内到外分别对L、K和S进行网格搜索。固定上述参数以外的其他超参数设置，包括迭代次数、批数等，根据式(10)预设3个参数的取值范围，其中，网格搜索范围i与Smax需要根据预测效果由人为经验设定，m表示沉降时间序列长度。此外，学习率l也是模型训练过程中影响较大的参数，当学习率较高时，损失函数收敛较快，反之，损失收敛较慢。研究表明，随着损失函数收敛情况做动态调整的学习率可以使模型得到更好的预测结果，因此，本文试验中采用衰减学习率的方式，将学习率按照实际效果每迭代20次乘以一个0.1的衰减系数。

1.2.3 网络预测

Ypred{y1,y2,…,yn}

(11)

式中，Ypred表示模型对不同高相干点预测结果的集合。最后，通过计算网络训练及网络预测过程中输出结果Ypred与真实样本标签Y的偏差，定量地给出模型训练和预测的精度。具体表示为

(12)

(13)

(14)

式中，μ表示模型平均预测精度；MAE表示平均绝对误差；MAP表示平均实际沉降量。

1.3 对比预测模型

为验证本文方法与现有时间序列预测方法相比所具有的优势，将LSTM模型与传统的时间序列预测模型、机器学习模型进行试验对比，选择模型建立时间与预测误差作为评价指标。为降低时间成本，试验数据采用统一的数据源(见后文)。

对于传统的时间序列预测模型，选择二次指数平滑(second exponential smoothing method,SES)、自回归移动平均(autoregressive integrated moving average,ARIMA)、多元线性回归(multiple linear regression,MLR)模型进行试验对比。其中，二次指数平滑法是一种能够处理含有趋势性成分的时间序列分析方法[23]，平滑指数α的取值大小决定了序列前期实际沉降值与预期值对本期预测值的影响；自回归移动平均法是时间序列分析中应用最广泛的模型之一[24]，模型可以表示为ARIMA(p,d,q)，其中p、d、q分别为自回归项数、差分次数、移动平均项数[25]。这3个参数通常可以通过观测自相关函数和偏自相关函数确定。该方法不直接考虑其他相关随机变量的变化。此外，多元线性回归也是一种广泛应用于预测任务的多因素分析方法[26]。在实际问题中，一个因变量往往受到多个自变量的影响，因此，多元的回归分析成了时间序列预测中受欢迎的方法。

对于机器学习模型，本文选择经典的支持向量回归(support vector regression,SVR)模型作为代表。该方法的思想是通过一个非线性核函数将多维输入映射到更高维度的特征空间后执行回归运算，进而得到与输出指标对应的非线性映射关系。在回归模型中，不同的核函数对拟合的结果会有较大的影响。本文选择常用的高斯径向基函数作为非线性核函数，本文采用Matlab2016中的支持向量回归工具箱完成该方法的预测试验，模型中惩罚参数C与核函数参数g通过交叉验证法求取最优设置。

2 沧州地区地表沉降预测结果与分析

2.1 数据源

选取近年来地表沉降现象严重的沧州地区[27]为研究区域。以2017年1月至2019年12月获取的80期Sentinel-1A影像为遥感数据源，采用自主研发的多主影像相干目标小基线(multiple master-image coherent target small-baseline interferometric SAR,MCTSB-InSAR)技术[28]开展前期数据准备工作。最终反演得到430 476个高相干点的沉降时序，其中每个观测点位拥有80个形变记录。为验证InSAR测量结果的可靠性和精确性，采用沧州地区国家二等水准数据进行对比验证。结果表明，本文数据源的反演结果精度为7.2 mm，足以支持本项研究[29]。Sentinel-1A影像时空基线参数如表1所示。对时间基线序列的平稳性检验结果表明，一阶差分后的时间间隔是平稳的，因此忽略了非等时间间隔对预测误差的影响。

表1 Sentinel-1A影像时空基线参数

2.2 试验结果

采用上述形变反演结果，对每个观测点的沉降时序进行了预处理，共得到容量为430 476的训练样本。根据实际训练情况，本文中i与Smax分别设定为7与100时足以发现最优的网络参数。首先通过网格搜索算法分析了样本输入、输出长度对预测效果的影响。图4为不同样本划分方式下的预测结果，其中，网络层数设置为3，隐藏层神经元数量设置为30。平均绝对误差热力图表明：随着输出序列长度的增加，不同样本输入长度下的模型误差均有所升高，其中，每个网格数据表示对应样本划分形式下多步预测的平均预测误差。图5进一步表示了对多步预测结果的误差分析。篇幅所限，仅以输入序列长度为60、预测序列长度为6示例。折线图表明：随着预测序列时间轴的推移，相应时刻的各项误差均有所降低，但对于同一时刻的预测结果，相同样本情况下单步预测的误差更低。在Radarset 2影像数据中发现了相同的规律，因此，受折线图与热力图中的显著趋势的启发，本文在网络构建中优先采用单步预测方式。

图4 样本划分长度与平均预测误差的网格搜索结果(K=30,S=3)Fig.4 Grid search results of sample parameters and mean absolute error(K=30,S=3)

图5 单步预测与多步预测中不同时刻的各项误差表现(L=66，Y1=6，Y2=1)Fig.5 Error performance of different time in single step prediction and multi-step prediction(L=66，Y1=6，Y2=1)

本文进一步分析了单步预测中不同网络参数下的预测效果。由于LSTM网络可以学习长距离的时间序列数据，因此，尽可能取较大的样本长度以获取更好的预测效果(L=79)。分析不同参数设置下的结果可以发现，模型预测精度并非一直与模型复杂程度正相关，而是在局部存在较优的组合，当网格搜索范围固定时，最优参数的分布趋向于一致。为充分挖掘样本长度对模型预测效果的影响，本文进而用累计沉降及差分沉降两种数据对不同样本长度下的单步预测结果进行了分析。从图6可知，随着训练样本长度的增加，网格搜索局部最小预测误差均逐渐降低。此外，两种沉降数据之间的预测误差差异反映了LSTM模型更擅长对平稳沉降时序进行预测。值得注意的是，差分沉降数据在输入长度大于42以后预测误差逐渐提高。这表明并非输入时序长度越长效果越好，很可能较远时刻的沉降信息对当前时刻的预测存在可忽略的关联，一味地输入较长时序反而引入了一定的噪声误差。

图6 训练样本长度与平均预测误差的关系(K=3,S=40)Fig.6 Relationship between training sample length and average prediction error (K= 3,S= 40)

基于上述试验分析，最终确定LSTM预测模型参数组合如表2所示。

表2 最优模型参数组合搜索结果

在上述参数设置下，对沧州地区地表沉降的预测试验取得了非常好的效果。差分(累计)形变量平均绝对误差可控制在0.3 mm以内，完全满足现有InSAR数据处理规范的精度要求[29]。

图7从整幅影像的尺度展示了对沧州地区的沉降预测结果。结合真实形变的大尺度表达，可以发现本文的预测结果与真实形变高度吻合，沉降漏斗显示清晰且大部分高相干的预测误差在±0.5 mm以内。算法运行结果显示，430 476个观测点中，最大差分(累计)形变量预测误差为8.81 mm，平均预测精度达到67.4%，相关指标的计算方法表示为式(12)。因此，本文提出的模型预测结果与实际沉降量相比偏差较小，能够反映地表沉降随时间变化的基本规律，预测结果具有足够的可信度。

图7 沧州地区差分形变的预测结果Fig.7 Prediction results of differential deformation in cangzhou area

2.3 方法对比

对于本文并列分析的其余4种预测方法，均采用网格搜索法寻找了最优的参数设置，并详细记录了模型的运行时间以及预测误差，具体参数设置及预测效果见表3。

从表3可以看出，相比前3种基于数理模型的预测方法，在预测效果方面，LSTM模型的(差分)累计沉降量平均预测误差在0.3 mm以内，预测标准差及均方误差也一致低于传统时序预测方法，表明本文基于深度学习的预测模型精度高且具有较好的稳健性。其中，ARIMA模型需要对每一个高相干点的沉降时序进行一次建模，在参数优化时由于需要大量的时间成本(表3中该方法的建模时间为抽样预估值)，并不适合应用到大范围的地表沉降预测中。而相比作为机器学习代表的SVR模型，本文方法在建模时间上降低了89.6%，平均绝对误差降低了67.4%，在各项评价指标上均具有更好的表现。分析上述试验结果可知，基于LSTM的大区域地表沉降预测方法精度较高，时间成本较低，是一种更为满足生产安全需求的方法。

表3 不同预测模型的试验结果对比

2.4 空间分析

InSAR时间序列分析对于揭示宏观的地表形变格局、分异性及其演化规律提供了重要参考，而单个高相干点的预测结果意义并不大[30]。为探索本文时序预测模型的有效性，利用ArcGIS等工具对预测结果及历史沉降信息的空间统计特性进行对比分析。对于时序预测结果间存在的空间自相关、分层异质、空间格局等特性，分别采用经典的Moran’s I、Getis-Ord Gi*、q-统计、最邻近指数NNI等指标来衡量。结果表明，本文方法的预测结果并未显著改变历史沉降的空间统计特性，即仍然保持了原始InSAR反演结果的形变格局，这从空间上确保了深度学习方法在地表沉降预测上的可行性。详细的空间分析结果如表4所示。