轴承钢大方坯凝固组织模拟

2021-04-01白雪松孙彦辉

工业加热 2021年2期

李翔，白雪松，孙彦辉

(1.南京钢铁股份有限公司科技质量部，江苏南京 210035； 2.北京科技大学，北京 100083)

GCr15中碳含量达到1.0%、铬含量为1.45%作为一种高碳铬合金钢，由于其高碳的特性，两相区长度较宽，容易出现裂纹、偏析和疏松等缺陷[1]。而铸坯凝固组织的致密度可以在一定程度上反映铸坯内部质量的好坏，柱状晶致密度和等轴晶致密度与铸坯缺陷(裂纹、偏析、疏松)有着紧密的关系，因此有必要对铸坯凝固组织的致密度进行研究。本文利用ProCAST中元胞自动机-有限元耦合模型(CAFE法)，对320 mm×480 mmGCr15轴承钢大方坯凝固组织进行数值模拟，并研究了不同工艺条件(拉速、过热度)对铸坯柱状晶和中心等轴晶致密度的影响。

1 模型的建立

CAFE法是有限元法FE与元胞自动机法CA的耦合，是在枝晶生长动力学的基础上，对铸坯的温度场分布、柱状晶和等轴晶的形态变化进行模拟计算的[2]。

1.1 形核模型

模拟采用由Rappaz[3]等提出的基于高斯分布的连续形核模型，该模型忽略枝晶破碎和液相表面氧化等形式形成的晶粒核心，同时忽略液相流动对晶粒形核的影响，在给定的过冷度ΔT条件下，给出了晶粒密度n(ΔT)随过冷度的变化[4]，如下所示：

(1)

式中，某一过冷度ΔT下晶粒密度n(ΔT)可通过积分得到，计算公式如下所示：

(2)

式中：ΔT为钢液过冷度，K；nmax为最大形核密度，面形核密度单位为m-2；ΔTσ为形核过冷度标准方差；ΔTmax为平均形核过冷度。

1.2 枝晶生长模型

在实际金属凝固过程中，晶体的生长不仅受到动力学过冷的影响，而且还受成分过冷的影响。枝晶尖端的总过冷度ΔT由以下四方面能量组成[5]：

ΔT=ΔTc+ΔTt+ΔTr+ΔTk

(3)

式中：ΔTc为成分过冷度，℃；ΔTt为热力学过冷度，℃；ΔTr为固-液界面曲率过冷度，℃；ΔTk为生长动力学过冷度，℃。式(3)中的ΔTt、ΔTr、ΔTk项在大多数合金中都可以不予考虑。本模型中采用KGT[6]模型计算枝晶尖端生长速度，其主要关系式为

(4)

(5)

(6)

(7)

(8)

式中：Γ为Gibbs-Thomas系数；D为扩散系数；m为液相线斜率；k为分配系数；c0为钢液初始浓度；G为温度梯度；Ω为溶质过饱和度；Pe为贝克来数；将式(4)～式(8)联立并拟合后便可得到枝晶尖端生长速度的数学表达式：

v(ΔT)=a2ΔT2+a3ΔT3

(9)

式中：ΔT为过冷度，℃；a2、a3为拟合三次多项式的系数。

1.3 模拟参数的选择

本次模拟采用平面移动法，选取平面为铸坯横截面，其大小为320 mm×480 mm。表1为GCr15中主要成分。采用ProCAST软件中CAFE模块进行凝固组织模拟，在整个模拟过程中Gibbs-Thompson系数[7]取3×10-7m·K；而对于具体形核参数的选择如表2中数据所示；钢中C、Mn、P、S、Si、Cr等元素对模拟结果的影响也纳入考虑，对于溶质元素参数[8-10]选择如表3所示。ProCAST软件的CAFÉ模块可以通过表3中的数据计算得出枝晶尖端生长动力学参数，其结果为a2=1.364×10-6m·s-1·K-3、a3=6.367×10-7m·s-1·K-3。

表1 钢种的主要成分 %

表2 高斯分布参数

表3 主要溶质元素参数

2 模型的验证

2.1 温度场模拟结果的验证

采用CAFÉ法对铸坯凝固组织进行模拟，首先要计算出铸坯温度场的模拟结果。因此要验证凝固组织模型的准确性，首先要对凝固传热模型的准确性进行验证。图1为温度场模拟结果与红外测温结果的对比图。图1中分别显示了铸坯窄面及角部温度变化的模拟结果，与在距弯月面10、12、14、16 m处铸坯窄面及角部的红外测温结果。从图1中可以看到两者结果基本吻合，温度场模拟结果较为准确。

图1 温度场模拟结果与红外测温结果

2.2 凝固组织模拟结果验证

依照实际生产过程中的连铸工艺参数(拉速0.54 m/min、过热度18 ℃、比水量0.16 L/kg)对ProCAST软件中CAFÉ模块进行设置，模拟出的铸坯微观组织形貌如图2(a)所示，铸坯经过热酸侵蚀后的低倍组织如图2(b)所示，可以看到图2(a)、图2(b)两图在柱状晶区与等轴晶区比例上基本一致，模拟结果较为准确。

图2 模拟结果与实际低倍结果

3 结果分析与讨论

3.1 凝固组织模拟结果分析

采用切片的方式将铸坯切分为若干个片层，通过对比不同片层间晶粒的变化规律的方式对铸坯凝固组织进行研究。具体切片结果如图3所示，从铸坯横截面一边开始向着铸坯中心方向每隔2 mm截取一个长80 mm、宽30 mm的截面，至铸坯横截面中心处结束。

图3 切片示意图

铸坯的致密度可以通过比较平均晶粒半径来衡量，即相同面积下平均晶粒半径越小，其致密度越大。柱状晶长轴与短轴相差较大，因此选择柱状晶纵断面致密度研究，可以在一定程度上反映一次枝晶间距的大小；而等轴晶长轴与短轴大小基本一致，因此可以选择横截面致密度作为等轴晶致密度来研究。图4为不同位置纵断面晶粒数目、平均晶粒半径、最大晶粒面积随距表面距离的变化情况。从图4中可以看出：在铸坯表面附近纵断面晶粒数目最多，在激冷层晶粒数目急速减少，在柱状晶区晶粒数目减小的速度开始放缓，当CET转变结束后等轴晶区晶粒数目虽仍有一定下降的趋势但变化极小；平均晶粒半径在铸坯表面附近最小，在凝固初期平均晶粒半径迅速增大，而在随后的柱状晶区增大速度放缓，在等轴晶区平均晶粒半径基本保持在一定范围内上下浮动；随着凝固时间的增长，最大晶粒面积在激冷层迅速增大，在柱状晶区增大速度放缓并在随后的混晶区有明显的下降，在等轴晶区最大晶粒面积的变化在整体上呈增大的趋势。铸坯凝固过程中CET转变最先在距离铸坯表面49 mm处发生，整个CET转变过程在距离铸坯表面86 mm处结束。

图4 不同位置纵断面晶粒数目、平均晶粒半径、最大晶粒面积

3.2 柱状晶致密度研究

工艺参数的改变会引起铸坯凝固组织发生改变，使得铸坯柱状区范围不同，为了避免表层细小等轴晶区和中心等轴晶区的影响，选取距铸坯表面15～45 mm的柱状晶为研究对象，研究不同工艺参数对铸坯柱状晶致密度的影响，模拟尺寸如图5所示。

图5 柱状晶区模拟具体位置

图6(a)为过热度对铸坯柱状晶区的影响，从图6(a)中可以看出随着过热度的增大，柱状晶尺寸增大。图6(b)为所选柱状晶区域模拟统计结果，可以看出随着过热度的增大，相同面积下，柱状晶横断面平均晶粒半径由1.613 03 mm增加到1.637 30 mm，其中在过热度为22 ℃时平均晶粒半径最小为1.602 22 mm。图7为铸坯柱状晶区不同位置纵断面晶粒平均半径变化情况，从图中可以看出，过热度增加，同一位置柱状晶平均半径增大，柱状晶纵断面致密度减小；越向铸坯内部，柱状晶平均半径越大。

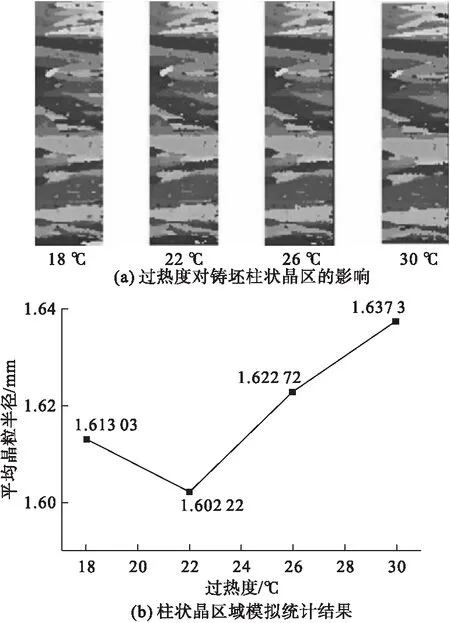
图6 过热度变化对柱状晶区的影响

图7 过热度变化对平均晶粒半径的影响

拉速对柱状晶区的影响如图8(a)所示。图8(b)为不同拉速条件下柱状晶区横断面模拟统计结果。从图中可以看出，平均晶粒半径整体上随拉速的增大而增大，且拉速从0.5 m/min提升到0.54 m/min，平均晶粒半径增长的最大，由此可得保持拉速在0.5 m/min以下能获得较大的柱状晶致密度。

图8 拉速变化对柱状晶区的影响

3.3 等轴晶致密度研究

铸坯等轴晶区的致密度等轴晶晶粒的长轴与短轴基本一致，因此平均晶粒半径也可以在一定程度上反映等轴晶晶粒的大小。不同工艺条件下等轴晶比例不同，为了避免柱状晶影响，选取所有工艺条件下铸坯公共等轴晶区为研究对象，如图9所示，选取中心区域面积为80 mm×80 mm为研究对象。

图9 中心等轴晶模拟具体位置

图10(a)为不同过热度下铸坯中心等轴晶区凝固组织模拟结果。图10(b)为不同过热度下中心等轴晶凝固组织模拟统计结果，从图10(b)中可以看出，当过热度由18 ℃增加到30 ℃，平均晶粒半径由1.944 99 mm减小到1.911 44 mm。铸坯中心等轴晶致密度随过热度的增大而增大。

图10 过热度变化对等轴晶区的影响

图11(a)为不同拉速下铸坯中心等轴晶区凝固组织模拟结果。图11(b)为不同拉速下中心等轴晶凝固组织模拟统计结果，从图11(b)中可以看出随着铸坯拉速的增加，平均晶粒半径整体上呈上升趋势，但变化不大，拉速的变化对平均晶粒半径影响较小。当拉速由0.45 m/min增加到0.6 m/min，平均晶粒半径仅由1.940 2 mm增加到1.940 9 mm。