极端温度下含隙铰柔性帆板展开位置精度分析
2021-03-31邱雪松丁锡浩任志博
邱雪松,商 阔,丁锡浩,任志博
(燕山大学机械工程学院,秦皇岛 066004)
0 引 言
太阳能帆板为空间机构提供能量,是月球车等航天器的重要组成部分。考虑发射状态等因素,太阳帆板通常是折叠态储存、工作状态时展开,故其展开功能的可靠性一直受到高度关注。可展帆板可靠性是指当外部环境发生改变,可展帆板能否顺利展开,以及展开后末端位置能否达到预设位置。众所周知,月球表面存在极端温度及温度差[1],其引发金属热胀冷缩,改变铰链间隙,是影响帆板展开可靠性的重要因素之一。
目前,国内外学者从不同角度、不同机构类型针对空间可展机构的可靠性进行了研究工作[2]。余德文等[3]从分析装配误差和灵敏度的角度出发对可展机构进行研究,解决了其无法精准定位和定量调整的问题;李团结等[4]通过结构优化提高可展机构的可靠性;Zhang等[5]通过分析含间隙铰的单个帆板的振动进行了可靠性研究;Li等[6]分析了阻尼、摩擦等因素对帆板展开可靠性的影响;更多学者以多体动力学为基础建立串联两级含间隙帆板模型,深入研究含间隙铰链可展帆板展开的可靠性及动力学性能[7-9];利用随机有限元法,吴建云等[10]探讨了铰链锁定位置偏差随机性对帆板展开精度的影响。以日本工程测试卫星VI(ETS-VI)为研究对象,Misawa[11]提出了一种预测卫星天线展开可靠性的分析方法。针对扭簧驱动式可展太阳帆板机构,杨翊等[12]学者通过研究系统可靠性与单元可靠性之间的关系给出了一种可展机构可靠性分配方法;肖宁聪等[13]学者则通过建立故障树方法查找太阳帆板展开失效原因,并从静力矩裕度、力矩做功等角度分析可靠性。陈列民[14]将太阳帆板假设为理想刚体,构建以展开角度为变量的函数,提出了一种计算帆板展开运动的方法。基于应力-强度理论刘志全等[15]建立驱动力矩与阻力矩关系功能函数,提出了使用大量试验数据作为样本分析太阳帆板展开可靠性的方法。以故障案例作为分析数据,使用FMEA分析方法统计分析,高俊东[16]找出了太阳翼展开可靠性的影响因素,定性地提出以连接架强度、基板强度、静力裕度等9个参数作为评价太阳翼展开可靠性的度量指标。
综上,学者们从影响因素的随机性、故障原因的多样性等角度,利用不同方法对空间可展机构可靠性进行了研究。研究多考虑机械结构及驱动等系统要素,对于环境温度因素考虑较少。
本文以可展帆板末端位置误差为评价指标,衡量帆板展开末端位置可靠性。通过建立环境与帆板材料及铰链的关系函数,构建考虑铰间隙和帆板柔性的可展帆板可靠性模型,分析极端温度对可靠性的影响,为确定满足机构展开可靠性最优的环境温度范围提供理论参考。
1 极端温度下重复可展帆板末端位置可靠性
1.1 重复可展帆板组成及传动原理
两级同步月球车含间隙柔性可展帆板由一级帆板、二级帆板、同步传动机构组成,参见图1。其中,同步传动机构采用绳系内错式传动,传动绳内错布置系于两级铰链A,B处,伺服电机驱动一级帆板转动,借助内错绳摩擦带动二级帆板转动,完成同步异向折展[17]。

图1 重复可展帆板原理图Fig.1 Schematic diagram of repeatable windsurfing
1.2 极端温度对帆板变形和铰链间隙的影响
帆板变形和铰链间隙是影响帆板展开精度及可靠性的重要因素。相较于帆板处于折叠状态和展开状态的时间,其展开过程时间极短,故提出假设:
1) 可展机构不工作时,随着月表温度变化,帆板材料属性和铰链间隙量随之变化。
2) 展开过程中,材料属性和铰间隙量不变。
1.2.1环境温度与帆板变形关系描述
泊松比和弹性模量是表征帆板材料机械性能的主要参数。二者随温度的变化可反映温度对帆板材料属性的影响。月球车可展帆板的基体材料是铝合金。由文献[18-19]可知,铝合金的泊松比随温度的变化很小,但温度对弹性模量影响较大,变化曲线如图2所示。因此进行动态特性分析时,主要考虑温度对材料弹性模量的影响即可。
通过Matlab数值拟合,得到铝合金的弹性模量和温度之间的函数表达式(见式(1)),其拟合后铝合金的弹性模量随温度变化曲线如图3所示。
E=-2.9×10-7T3-7.8×10-5T2-0.039T+70
(1)
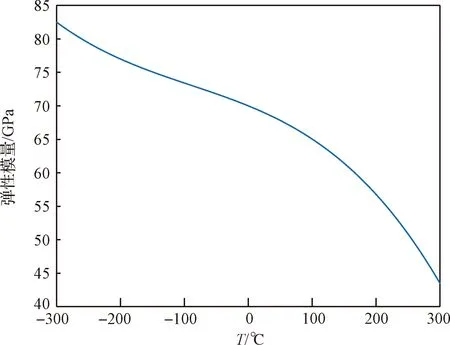
图3 铝合金弹性模量随温度变化曲线Fig.3 The curve of aluminum alloy elastic modulus with temperature
1.2.2铰链结构与铰链间隙变化描述
考虑运载空间等要素,可展帆板铰链结构通常采用滑动轴承,即铰链由轴承座、轴套和销轴构成,其中轴套与轴承座间为过盈配合,轴套与销轴间为间隙配合。建立如图4所示铰链模型,分析温度对铰链间隙的影响。

图4 铰链配合关系示意图Fig.4 Schematic diagram of hinge coordination
铰链结构温度场的形成有两个因素:月表环境温度和铰链构件间摩擦生热。因帆板展开速度很慢,铰链构件摩擦产生的热量有限,相较于环境温度可忽略,故仅分析环境温度所形成的温度场。
铰链的初始间隙由构件间的配合关系决定,与配合关系相关的则是构件的结构尺寸。对于折展频率很低的帆板,折展过程中影响结构尺寸的主要因素是环境温度,可以忽略磨损的影响。因此通过分析配合关系和温度变化对于铰链构件尺寸的影响可以确定铰链间隙变化规律。
1) 配合关系对铰链结构尺寸的影响
根据弹性薄壁理论分析,铰链间隙大小受轴套外径与轴承座孔过盈配合量Ii_h影响,二者因配合产生相互作用力Pi_h为
Pi_h=
(2)
式中:Ei_h,Ew_h为轴套、轴承座的弹性模量;μi_h,μw_h为轴套、轴承座的泊松比;Dw为轴承座初始外径;Dw_h为轴承座配合后外径;Dn_h为轴套配合后内径。
进而引起轴套外径变化量
Δi_h=
(3)
2) 温度变化对铰链结构尺寸的影响
因月表温度变化,铰链产生径向间隙变化。根据热力学原理,径向间隙变化量为
ΔT-h=(Γi-h-Γn-h)Dw-h(To-Ta)
(4)
式中:Гi_h,Гn_h为轴套、轴颈的线性膨胀系数;Ta,To为变化前、变化后的月表温度。
受交变温度影响,轴套外径与轴承座孔的过盈配合量Ii_h的变化量为:
ΔIi_h=(Γi_h-Γw_h)Dw_h(To-Ta)
(5)
式中:Гw_h为轴承座的线性膨胀系数。
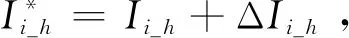
考虑交变温度的作用,铰链径向间隙变化量为
(6)
综上,可确定月表温度场下间隙量大小
Ph_t=ΔPd_h+Pd
(7)
式中:Pd为铰链初始间隙。
1.3 极端温度下柔性可展帆板含间隙动力学模型
应用运动弹性动力学分析方法建立月表温度下柔性可展帆板含间隙动力学模型[20]。
(8)

因建模过程中,帆板柔性及铰链间隙已被引入质量矩阵M,刚度矩阵K与广义力矩阵Q,故温度因素的引入通过描述温度与间隙的关系及柔性帆板等效模型即可。
1.3.1帆板展开过程铰链间隙
帆板展开过程中,铰链间隙动态变化,表现为轴套与销轴发生弹性碰撞,并因弹性变形而产生相对侵入。引用文献[20]中轴套与销轴弹性碰撞变形描述,月表温度下二者碰撞深度为
(9)
式中:Ph_t为月表温度下铰链间隙;ex,ey为直角绝对坐标系下,销轴中心与轴套中心沿x,y两方向偏心值。
轴套与销轴的接触碰撞力FP[21]为
FP=(Fn+Ft)+
(10)
其中,下标“+”意义:当δ≥0,轴套与销轴发生接触碰撞,FP>0;当δ< 0,轴套与销轴无接触碰撞,FP= 0。Fn,Ft为法向碰撞力、切向摩擦力,表达式参见文献[21];Fn,Ft均由δ描述,δ与月表温度影响下的间隙Ph_t具有函数关系,如式(9)所示,故式(10)即为月表温度下铰链间隙处的接触碰撞力。
1.3.2柔性可展帆板的等效模型
月球车柔性可展帆板的基板采用蜂窝状多层基板,为便于分析,将蜂窝状多层基板等效为各向同性薄平板。根据Hoff等刚度理论[21]对帆板进行等效处理,各等效参数见表1。

表1 各参数的等效处理Table 1 Equivalent treatment of each parameter
1.4 极端温度下柔性可展帆板重复展开末端精度
帆板重复展开精度是月球车可靠工作的重要保证。由于制造和装配误差、环境温度变化等因素,导致帆板的几何属性和间隙等系统参数具有一定的随机性。因此,采用拉丁超立方抽样处理,获得样本导入动力学模型进行分析。
1.4.1可展帆板末端位置极限函数
设帆板可展机构中有n个互相独立、服从正态分布的系统随机变量X=[X1,X2, …,Xn]T。记二级帆板末端点位置允许误差为ΔSy,t时刻二级帆板末端的实际位置误差为S(t),ΔSy和S(t)均服从正态分布。二级帆板末端位置极限函数为:
Z=g(X)=ΔSy-S(t)
(11)
1.4.2可展帆板理论末端位置期望
可展帆板的理论末端位置是指不考虑铰链间隙和帆板柔性,帆板展开的末端位置坐标M(xM,yM)。
(12)
式中:l为铰链A中心距绝对坐标系xoy原点的距离。
设l1,l2是相互独立、正态分布的系统随机变量。应用一次二阶矩法,将式(11)在各分量期望处进行泰勒展开并取一次幂,求得Z的期望和标准差分别如式(13)和式(14)所示:
μZ≈g(μX)
(13)
(14)
将式(12)代入式(13)得到可展帆板末端M在任意时刻t的位置期望
(15)
末端M的位置均值为
(16)
1.4.3可展帆板实际末端位置的期望
由于输入参数的随机性导致间隙-柔性耦合动力学模型具有强非线性、时变的特点,故在任意时刻t,系统输入参数与末端位置均为隐式函数关系。一次二阶矩法等经典方法不适用于隐式函数的直接求解分析[22],因此先采用BP神经网络算法对小样本进行自学习,进而拟合出任意时刻的隐式函数,再利用一次二阶矩法构造出末端位置的均值和方差。

已知系统输入X=[X1,X2, …,Xn]T,各参数相互独立且符合正态分布。输出层的输出即可展帆板末端位置为Y(X)=[yl(X)]T。任意t时刻输入量与输出量之间关系为:
(17)
故任意t时刻帆板末端实际位置误差为
S(t)=Y(X)-μSMI
(18)
对式(17)求偏导
(19)
式中:JYkZk表示Jacobi矩阵,表示第k层的输出值Yk对激活值Zk的偏导,k=1,2,3。
应用一次二阶矩法,得到任意t时刻,帆板末端实际位置误差期望和方差
(20)
1.4.4可展帆板末端位置可靠性计算流程
根据应力-强度干涉理论,构造t时刻帆板末端位置精度表达式
(21)
式中:β为可靠性指标,β=μZ/σZ为无量纲数。
设ΔSy的期望和标准差分别为μΔSy,σΔSy,则帆板末端实际位置误差期望和方差为
μZ=μΔSy-μyl
(22)
(23)
具体计算流程如图5所示。

图5 计算流程图Fig.5 Calculation flow chart
采用经典MC法检验前述方法的正确性。依据大数定理,将满足一定条件的样本个数n除以样本总量N,即R≈n/N作为精度的近似值。取样本N≈100/(1-R)以保证MC法计算的可靠性有效,具体流程如图6所示。
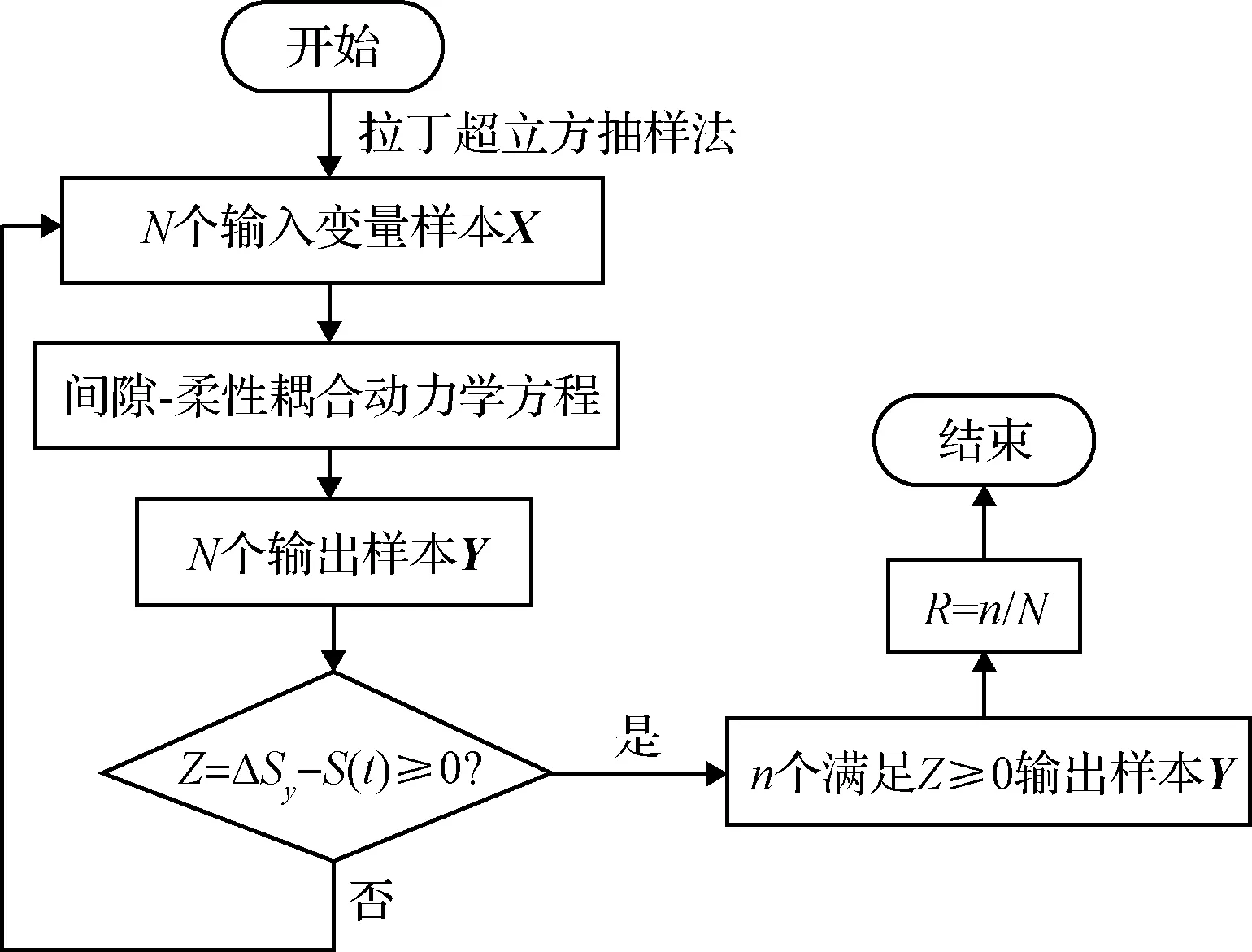
图6 经典MC法计算流程图Fig.6 Classic MC method calculation flow chart
2 算例求解
取原理样机的几何及物理参数值进行算例求解,具体数值见表2。

表2 样机参数值列表Table 2 Prototype parameter value list
2.1 温度对铰链间隙的影响
基于前述分析,分别采用数值方法和软件仿真求解,得到铰链间隙与温度的关系曲线,如图7所示。由图7可知,铰链间隙与温度的变化成正比关系,间隙大小随温度的增加而增加。

图7 间隙随温度变化曲线Fig.7 Gap change curve with temperature
2.2 温度对铰链特性的影响
不同月表温度下,铰链间隙及帆板的等效弹性模量如表3所示,其中轴衬材料为ZCuAl19Fe4Ni4Mn2。

表3 系统输入参数期望(20 ℃)Table 3 System input parameter expectations (20 ℃)
使用式δ(T+ΔT)·δ(T)≤0(T为温度)处理不同温度下铰链间隙偏心量,得到温度-碰撞次数、温度-碰撞变形量、温度-碰撞力、不同温度末端位置误差-时间关系曲线,如图8~图11所示。
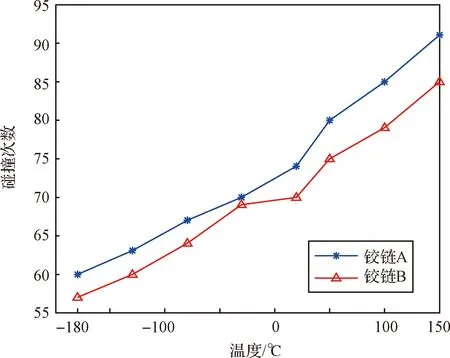
图8 温度-碰撞次数Fig.8 Temperature-number of collision

图9 温度-碰撞深度Fig.9 Temperature-depth of collision
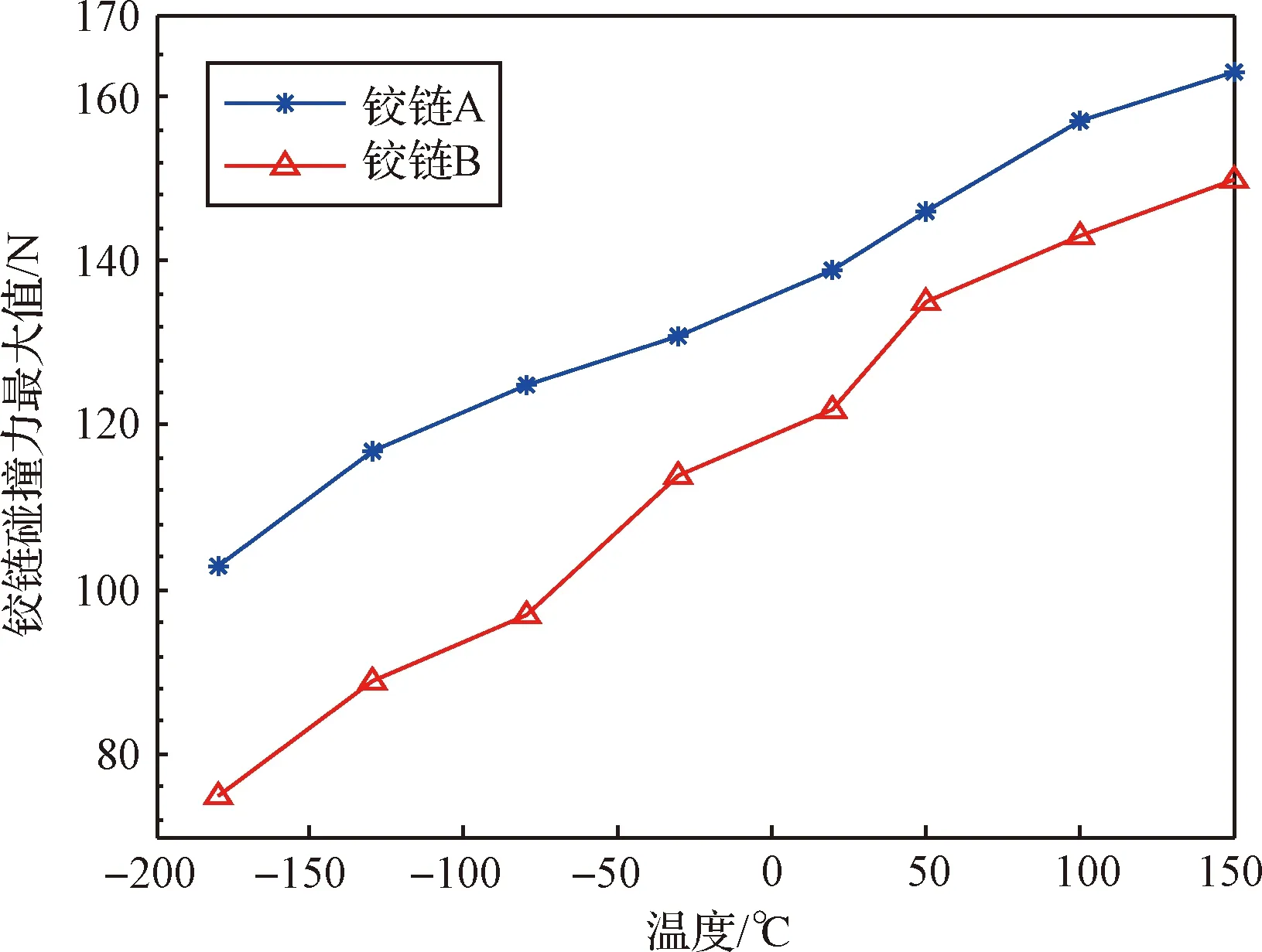
图10 温度-最大碰撞力Fig.10 Temperature-maximum collision force

图11 温度-末端位置误差Fig.11 Temperature-end position deviation
显然,温度的升高导致铰链间隙增大,间隙处碰撞频次、碰撞深度、碰撞力、末端位置误差增大,机构的运动精度将随之降低。
2.3 帆板末端位置可靠性分析
帆板折展机构由伺服电机驱动,故帆板展开运动规律由θ(t)表示。给定一级帆板展开运动规律θ1=0.25π(1-cos(0.2πt)),根据传动原理,二级帆板展开运动规律为θ2=-θ1。利用四阶变步长Runge-Kutta法、Newmark-β法求解方程组,可获得帆板末端位置曲线。
1) 输入变量的确定
对于柔性-间隙耦合作用下的可展帆板,其系统输入量包括两级帆板的弹性模量E1,E2,长度l1,l2,质量m1,m2,铰链间隙Pt1,Pt2。由于制造、装配、运转磨损、温度变化等因素导致铰链间隙随机变化,同时弹性模量亦随温度改变,进而影响长度参量,因此弹性模量、长度、铰链间隙均为随机变量。设上述系统输入变量相互独立,符合正太分布,系统输入参数的均值如表4所示。

表4 系统输入参数期望(20 ℃)Table 4 System input parameter expectations (20 ℃)
模型中有8个相互独立的输入量,其中6个是随机变量,选用300组样本来拟合系统输入随机变量与输出变量间的隐式函数关系。
2) 末端位置-时间曲线
分析不考虑铰链间隙及帆板柔性的理想状态和间隙-柔性耦合作用下的实际状态,绘制可展机构末端位置时间历程图,如图12所示。从图12可以看出,间隙-柔性的耦合作用导致帆板末端实际位置相对于理想位置产生了较大的位置偏差,降低了可展机构精度。
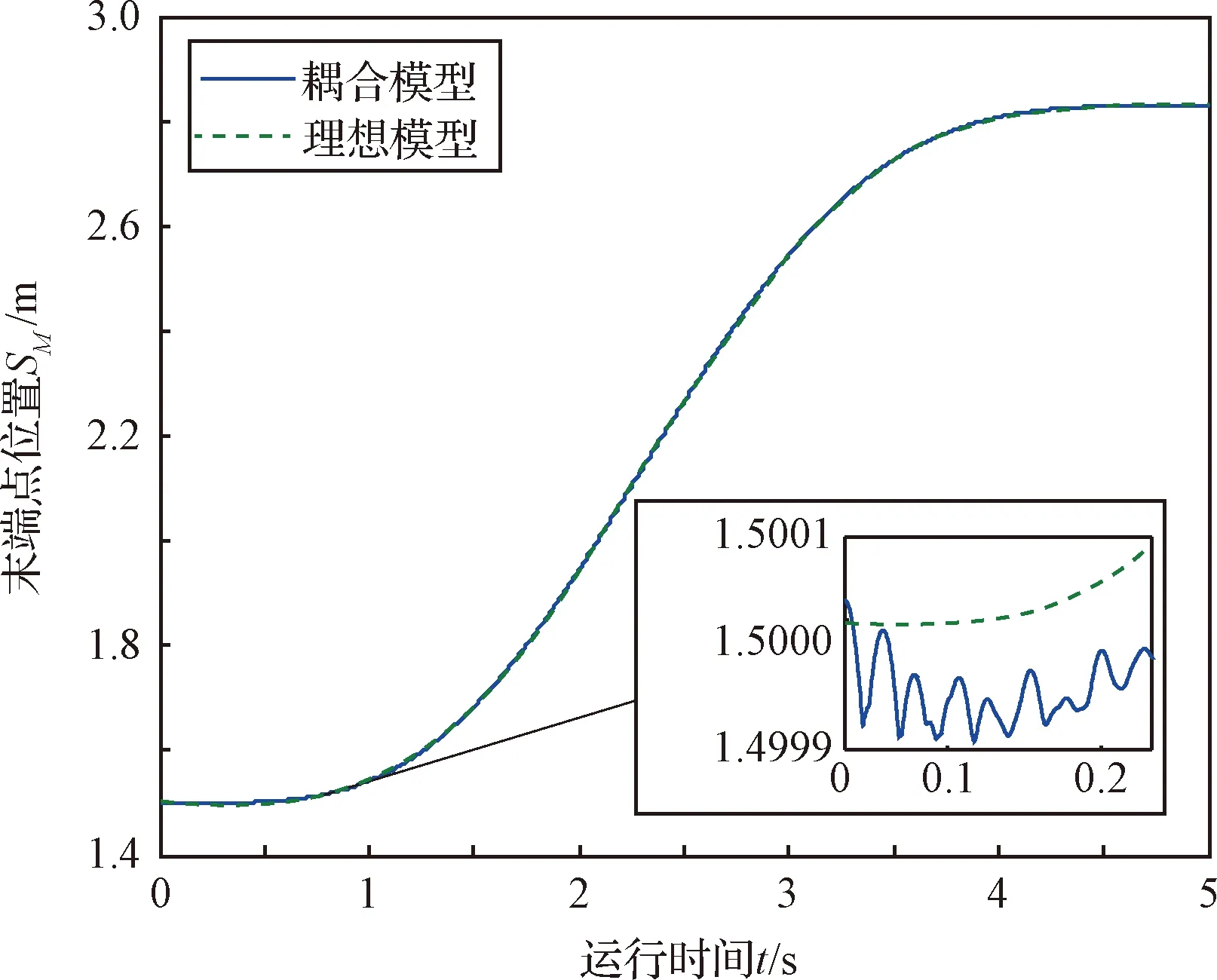
图12 帆板末端位移的时程曲线Fig.12 Time-history curve of the displacement of the end of the windsurfing board
分别应用经典MC数值方法和BP神经网络方法计算,绘制帆板末端位置时间曲线(见图13),从图13可以看出两条曲线比较接近,说明BP神经网络法能有效拟合帆板末端位置。
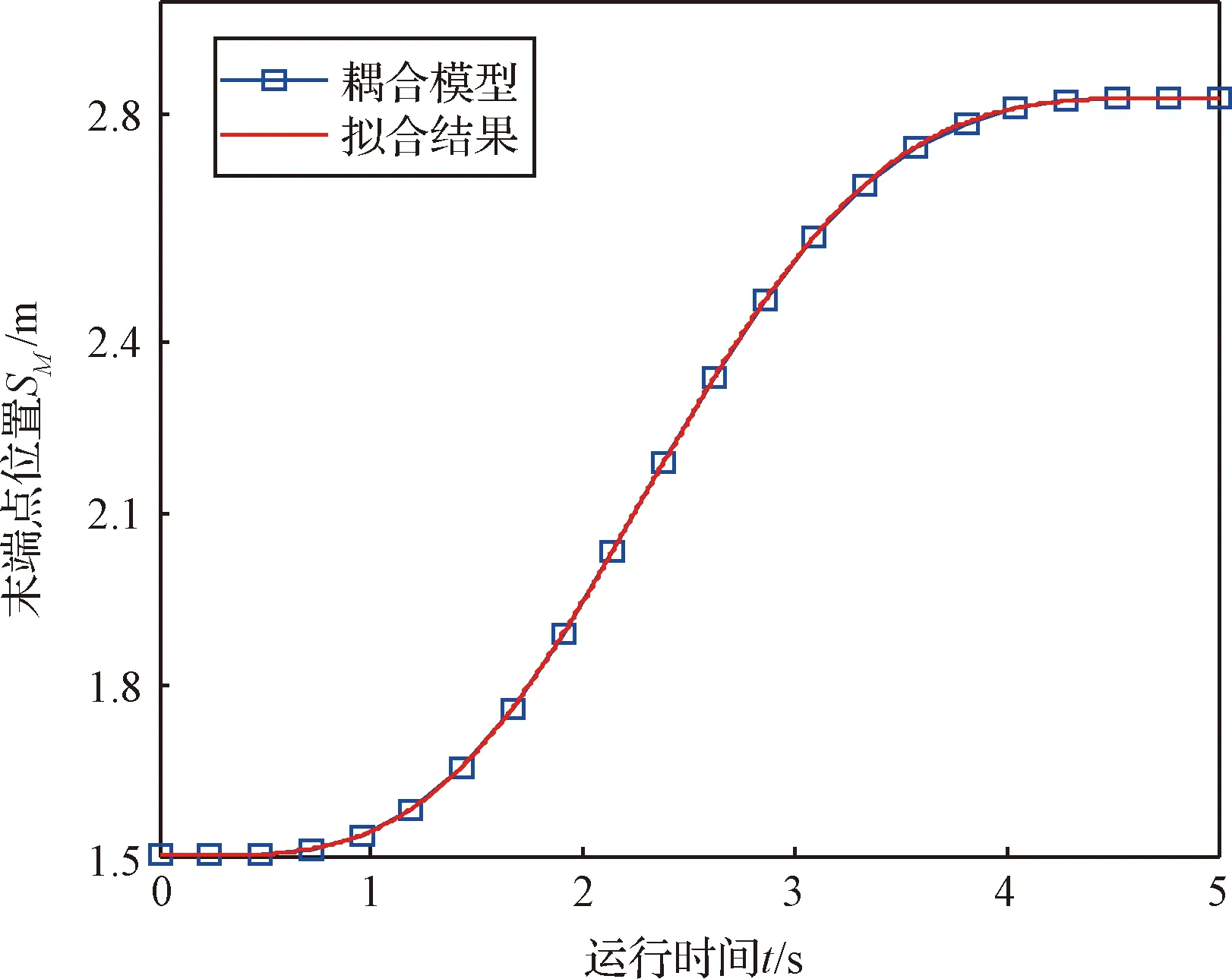
图13 帆板末端位移的对比图Fig.13 Comparison of the displacement of the end of the windsurfing board
应用BP神经网络方法,计算不同时刻帆板末端位置的期望和方差,如图14、图15所示。其中,末端位置误差最大值和最小值根据经验法则(empirical rule)求出。
3) BP神经网络模型验证
计算可展机构完全展开时(t=5 s)帆板末端点位置。设置模拟精度10-3,模拟运算最大次数105。经计算,第一隐神经元数量为20。拟合效果如图16所示。由图16(a)可知,模拟运算8984次后结果达到设定精度,图16(b)显示拟合结果与数值计算结果线性回归,两者的相关性达到0.99655。可验证建立的BP神经网络模型能准确拟合帆板末端位置。
4) 可展帆板末端位置可靠性
在完全展开时刻,计算帆板系统各输入随机参数对展开位置精度影响的灵敏度,如图17所示。
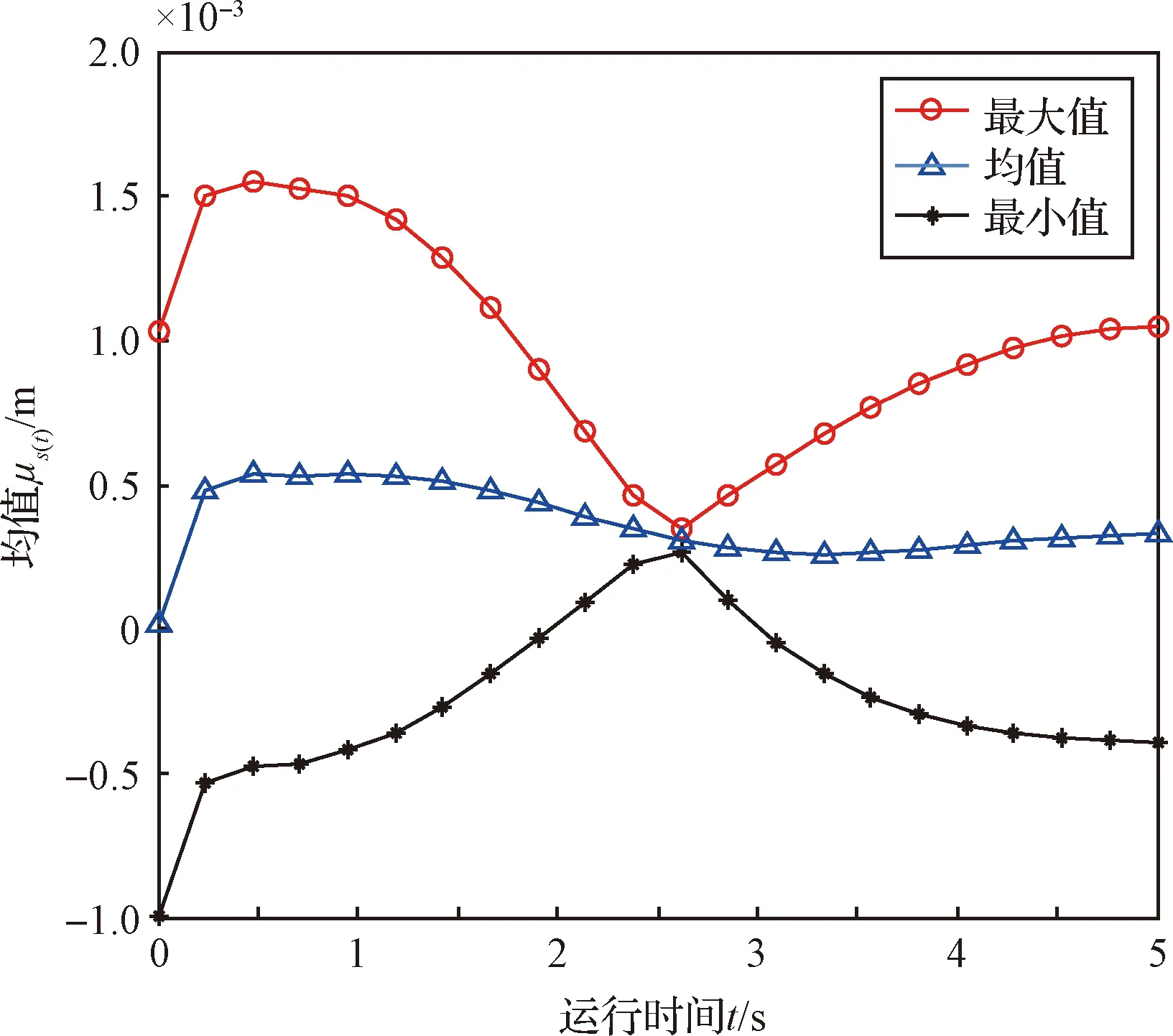
图14 帆板末端位移误差的均值Fig.14 Mean value of displacement error at the end of windsurfing

图15 帆板末端位移误差的标准差Fig.15 Standard deviation of the displacement error at the end of the windsurfing board

图16 拟合效果检验Fig.16 Fitting effect test

图17 各参量影响末端位置精度的灵敏度Fig.17 The sensitivity of each parameter affecting the accuracy of the end position
显然,在弹性模量、铰链间隙等各因素中,代表帆板柔性的弹性模量灵敏度远小于铰间隙的灵敏度,即铰间隙对帆板展开末端位置精度的影响最大。且对于串联的二级铰链机构,一级帆板与基座间的铰链间隙对机构精度的影响大于一级、二级帆板间铰链间隙的影响。
设可展帆板末端位置允许误差ΔSy的期望为μΔSy=8.0×10-4m,方差为σΔSy=1.0×10-5m,取各随机变量的变异系数0.01和t=5 s时刻,绘制不同温度下帆板末端位置可靠性变化曲线(见图18)。

图18 不同温度下帆板末端位置可靠性Fig.18 Reliability of windsurfing end position at different temperatures
由图18可知,温度变化对于帆板展开末端位置可靠性的影响较大。当温度区间为-30 ℃~20 ℃时,机构的可靠性最优,可达到0.98以上。
3 结 论
1) 通过建立帆板弹性模量、铰链间隙与温度的函数关系,获得了极端温度下间隙-柔性耦合的帆板展开动力学模型。定义了帆板展开末端位置误差作为评价指标。
2) 采用拉丁超立方抽样处理,获得了BP神经网络自学习样本;结合一次二阶矩法,推导出可展帆板末端位置误差的期望与方差;利用应力-强度理论构造了帆板展开末端位置可靠性模型。
3) 采用自主研制的二级重复可展帆板相关参数,进行了算例分析。结果表明,极端温度条件下,铰间隙对于位置精度的影响显著,温度区间在-30 ℃~20 ℃时,机构展开精度可靠性最优。
