反步法与神经网络融合的平流层飞艇轨迹鲁棒控制方法

杨希祥，杨晓伟，邓小龙

(国防科技大学空天科学学院，长沙 410073)

0 引 言

平流层飞艇是典型的低速临近空间飞行器，依靠浮力驻空，采用太阳电池和储能电池构成循环能源系统，采用电机驱动螺旋桨抗风，可实现月量级的区域超长航时驻留，也被形象的称为“平流层卫星”，在对地观测、通信广播、移动互联网、防灾减灾等领域具有巨大应用潜力[1-2]。

有效的飞行轨迹控制是实现区域长期驻留的核心挑战之一[3]。平流层飞艇总体布局、飞行原理、工作模式显著不同于飞机等飞行器，轨迹控制技术难度很高，主要表现在：属于大尺度柔性体(长度超100 m)，囊体气动外形变化等引起的未知因素多，非线性强，导致建立的动力学模型存在很大不确定性；飞行速度与环境风速在一个量级(一般不超过20 m/s)，受环境风场干扰影响大，且环境风速风向短期内存在多变特征；体积/惯量巨大(体积达几十万立方米)，执行机构控制力/力矩相对较小，具有明显的大惯量、长时延特征。

国内外学者针对平流层飞艇及具有部分相似特征的浮空飞行器轨迹控制问题开展了系列研究[4]，文献[5]对平流层飞艇姿态控制、轨迹控制等研究现状和难点挑战进行了综述分析，特别指出了不确定、参数摄动、风场影响等耦合因素制约。总体来看，现有研究方法大致可分为三类：基于线性化模型的轨迹控制方法、非线性轨迹控制方法和智能轨迹控制方法。

基于线性化模型的轨迹控制方法，往往是针对某一特征点的标称状态，将平流层飞艇动力学模型按纵向和横侧向解耦分离设计，采用线性化方法将非线性动力学模型线性化，然后设计线性控制系统[6]。Pais以低空飞艇为研究对象，分高度控制和航向控制两个通道，采用PI方法设计了轨迹控制系统[7]。Nagata等[8]研究了自调参的小型浮空器PID控制器设计方法，相对手动调参，控制性能得到改进。线性化轨迹控制方法简单，易于工程实现，但在模型参数及工作点发生变化、面临外部不确定扰动时，控制性能难以得到保证。

非线性轨迹控制方法，是指直接针对飞艇动力学模型，利用非线性控制方法实现轨迹控制[9]。滑模控制方法[10-11]和反步法(backstepping)是应用最广泛的飞艇非线性轨迹控制方法，其中，反步法通过递归构造闭环系统的李雅普诺夫函数，获得相对应的控制变量和控制律[12]，具有严反馈特点，鲁棒性好。文献[13]研究了平流层飞艇最优轨迹规划和跟踪，采用反步法设计了全局稳定的非线性轨迹控制器，研究中推力不受限；Vieira等[14]将反步法与滑模控制方法结合，用于飞艇轨迹跟踪，相对传统反步法和滑模控制方法，控制精度和鲁棒性进一步改善。

增益参数设置调整是反步法应用中的关键点，对轨迹控制精度和鲁棒性存在很大影响。本文提出采用神经网络进行寻优，实现增益参数动态自主调整，以更好应对平流层飞艇轨迹控制面临的外部风场扰动和系统模型参数不确定问题。

1 平流层飞艇轨迹控制问题建模

1.1 平流层飞艇动力学模型

平流层飞艇轨迹跟踪控制的目标是，使实际轨迹与参考轨迹之间的误差趋于零，因此，对于水平轨迹控制来说，控制器设计应使表征飞艇水平运动的状态量实际值与期望值一致。

为使平流层飞艇状态量具有统一性，采用Lagrange动力学模型[15-16]

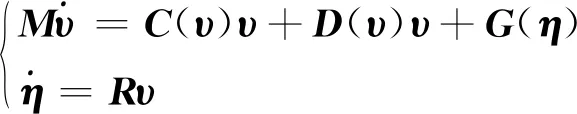
(1)

式中：υ=[u,v,r]T,η=[x,y,ψ]T为体坐标系下水平运动状态量的广义坐标；C为科氏力和向心力矩阵；D为耗散阻尼系数矩阵；G(η)为恢复力矩；R为惯性坐标系到体坐标系的转换矩阵;M为考虑附加质量的惯量矩阵，

将式(1)展开得到标量形式的非线性模型

(2)

式中：u，v分别为飞艇轴向速度和侧向速度；r为飞艇偏航角速度；x，y，ψ分别为飞艇在地面惯性坐标系下的位置和偏航角；Iz为飞艇绕体坐标系z轴的转动惯量；λ11=k11m，λ22=k22m，λ66=k66m， 其中k11，k22，k66为惯性因子，与飞艇外形尺寸有关；Fwind=[Fwind-x,Fwind-y,τwind]为风场导致的干扰力和力矩；Xw，Yw，Nw为气动力分量；F，τ为飞艇所受推力和力矩。

1.2 基于动力学模型的误差系统

对平流层飞艇非线性运动模型中的状态量进行同胚变换，将位置状态量变换为三个非线性状态量，即令

(3)

建立与速度状态量的关系

(4)

设参考轨迹为ηd=[xdydψdudvdrd]T，得到参考轨迹的非线性模型

(5)

式中：ud,vd,ud分别为参考轨迹对应的轴向速度、侧向速度和偏航角速度；xd,yd,ψd分别为参考轨迹在惯性坐标系中的位置和偏航角；Fd，τd为飞艇沿参考轨迹飞行时受到的力与力矩；Xw-d，Yw-d，Nw-d分别为飞艇沿参考轨迹飞行时受到的气动阻力、侧力与偏航力矩。因为参考轨迹是在理想条件下的，所以风场干扰项均等于零，且气动力与气动力矩均为常数。

轨迹的误差系统可表示为

(6)

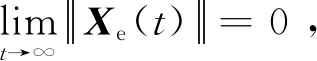
2 反步法与神经网络融合的控制方法

2.1 采用反步法的轨迹控制方法

反步法的基本思路是，将复杂的非线性系统分解成多个不超过系统阶数的子系统，然后为每个子系统设计满足Lyapunov稳定性理论的标量函数和中间虚拟控制量，最终集成起来完成系统总控制律的设计[16]。

考虑式(6)表示的轨迹误差系统，存在两个控制量：推力F和力矩τ，根据反步法的设计思路，将其分成两个子系统，分别为：(z1e,z2e,ue,ve)和(z3e,re)。对于第一个子系统，状态量z1e,z2e,ve的微分表达式中均含有re，所以如果第二个子系统能够达到渐近稳定，则re对状态量z1e,z2e,ve没有影响，因此，划分为上述两个子系统是合理的，后者影响前者，属于包含关系。

1)求解力矩项控制律

依据反步法设计步骤，首先求取第二个子系统的控制律，分析可知，其角速度项直接受控于控制力矩大小。

引入变量x1=z3e,x2=re,u=τ-τd，根据误差系统得到以下关系式

(7)

预选Lyapunov正定函数：

(8)

将x2作为x1的虚拟控制输入，计算正定函数的导数

(9)

式中：

y2=x2-α(x1)

(10)

其中,α(x1)为虚拟控制量，令

α(x1)=-k1x1，k1>0

(11)

式中：k1为控制增益参数。

得到正定函数导数值为

(12)

预选另一Lyapunov正定函数

(13)

同理可得

(14)

令控制律

(15)

根据式(7)～(10)，将控制律转换为关于输入变量re,z3e和增益参数的关系，即

u=-(Iz+λ66)·

(16)

进而得到力矩的控制律：

τ=τd-(Iz+λ66)·

(17)

2)求解推力项控制律

针对第一个子系统(z1e,z2e,ue,ve)，在求解得到力矩项的控制律后即保证了第二个子系统是稳定的，由于推力直接影响横向速度ue，而力矩对位置以及速度无影响，所以直接对推力和横向速度进行反步法设计。通过设计力与力矩项获得相应的控制律使得误差系统中的误差状态量渐近趋于零。

与力矩项控制律求解过程类似，引入变量x1=ue,u=F-Fd，得到推力关于ue的控制律

F=Fd-(m+λ22)(vr-vdrd)-

Xw-e-(m+λ11)k3ue

(18)

式中：k3也为控制增益参数。

2.2 采用RBF神经网络的增益参数寻优

第2.1节利用反步法设计的轨迹控制律中，控制增益参数k1,k2,k3对控制性能影响很大，且其确定和调整过程较为困难。为此，本节引入神经网络参数寻优的方式，将增益参数作为神经网络权值，根据输入输出之间传递函数以及实际输出与期望输出的差异，对网络权值进行动态更新，最终达到对参考轨迹的高精度跟踪控制，如图1所示。

图1 反步法与RBF神经网络融合的轨迹控制器Fig.1 Trajectory controller with combination of backstepping and RBF neural network

RBF神经网络是典型的局部神经网络，泛化能力强、收敛速度快，适用于非线性系统中对可控增益参数的快速寻找问题。RBF神经网络为三层网络结构[17]，中间隐含层的作用函数为高斯基函数，可以拟合任意的非线性函数。

控制增益参数寻优流程如图2所示，将轨迹状态量作为网络的输入层，增益参数作为网络权值项，隐含层输出为推力与推力矩，输出层输出为实际的轨迹状态量，根据期望与实际的状态之差作为网络权值的更新依据，当误差值达到精度要求则寻优结束，反之，则继续更新，直至满足控制精度需求。

图2 采用RBF神经网络的增益参数寻优流程Fig.2 Optimization process of control gain parameters with RBF neural network

3 仿真校验

3.1 仿真条件

参考轨迹为直线与圆弧的组合，前100 s作直线运动，中间250 s跟踪半径为20 km的圆弧运动，最后50 s作直线运动。给定参考轨迹初值，

[xd(0),yd(0),ψd(0),ud(0),vd(0),rd(0)]=

[0 m，0 m，0.02 rad，5 m/s,0 m/s,0 rad/s]

同时给出初始状态值，

[x0(0),y0(0),ψ0(0),u0(0),v0(0),r0(0)]=

[0 m，0 m，0 rad，0.1 m/s,0.1 m/s,0.1 rad/s]

给定风场干扰项

Fwind=[Fwind-x,Fwind-y,τwind]=

固定控制增益仿真中，直线段控制增益取值为k1=4,k2=3,k3=0.4，圆弧段控制增益取值为k1=6，k2=1，k3=0.12。

采用RBF神经网络对控制增益参数进行寻优的仿真过程中，控制增益参数初值取为：k1=k2=k3=0.01。

仿真过程所用其余主要参数见表1。

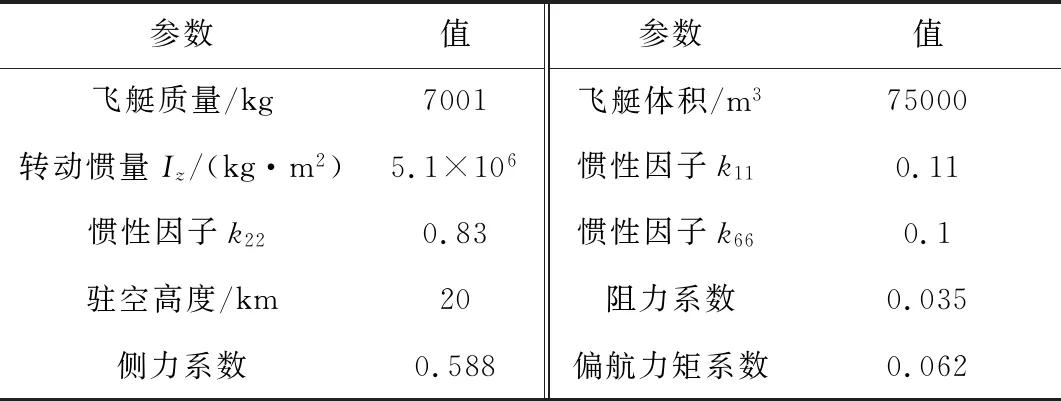
表1 主要仿真参数Table 1 Main simulation parameters

考虑平流层飞艇重心在体心下方，具有强滚转稳定性，忽略滚转运动。执行机构推力上限为1000 N，控制力矩上限为6000 N·m。

3.2 仿真结果与分析

固定控制增益时的轨迹跟踪结果和跟踪误差如图3～图5所示，从图中可以看出，针对外部变化风场，轨迹跟踪误差大，最大误差1.3 km，且振荡不稳定。

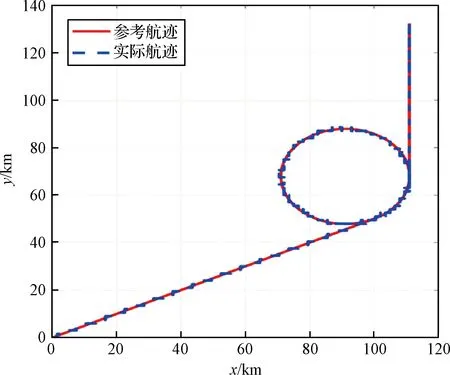
图3 固定控制增益时的轨迹跟踪结果Fig.3 Trajectory tracking results with fixed control gain

图4 固定控制增益时圆轨迹跟踪放大结果Fig.4 Amplification results of circular trajectory tracking

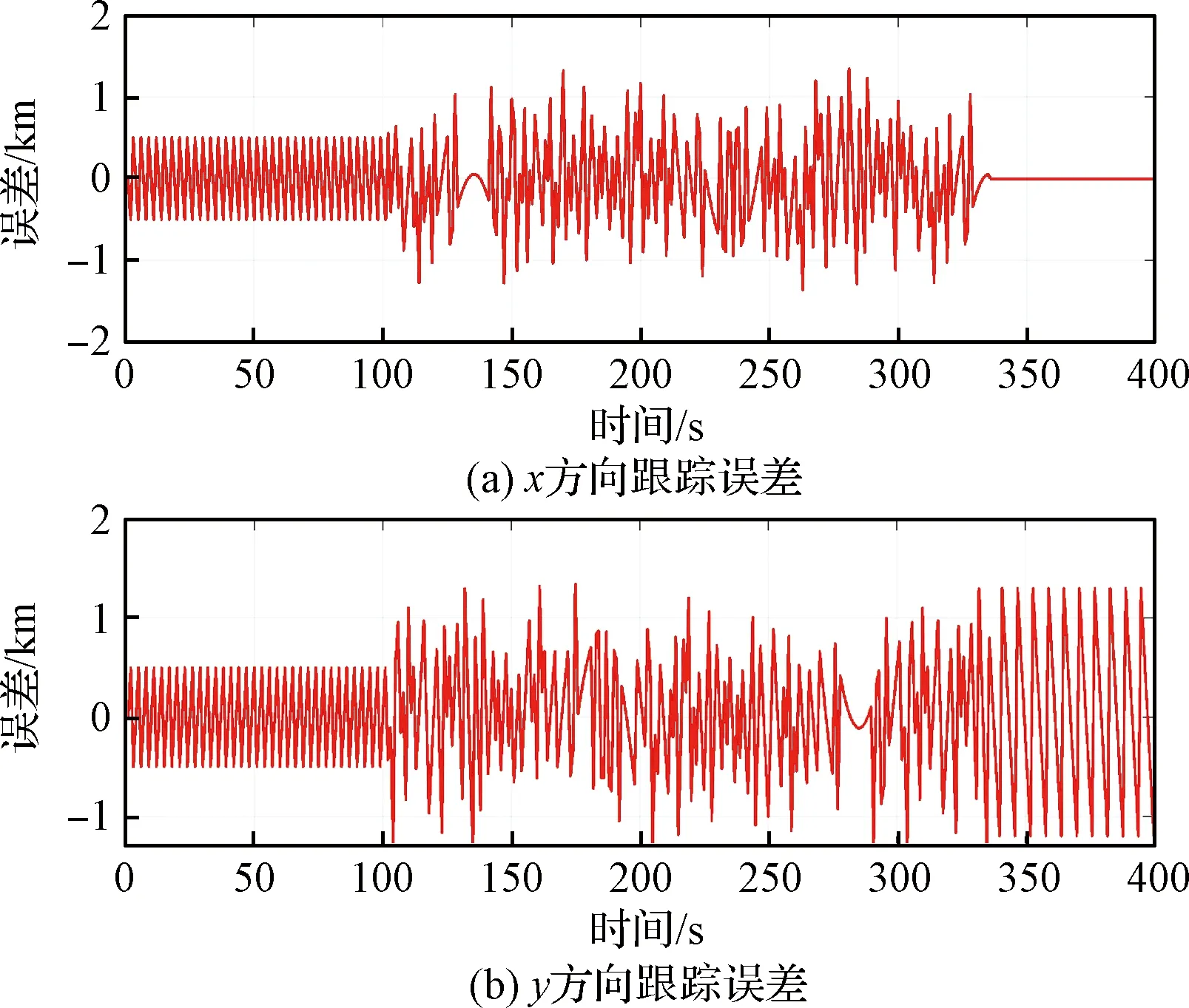
图5 固定控制增益时的轨迹跟踪误差Fig.5 Trajectory tracking error with fixed control gain

采用RBF神经网络对控制增益参数进行寻优的轨迹跟踪结果和跟踪误差如图6～图8所示，增益参数变化过程如图9所示。

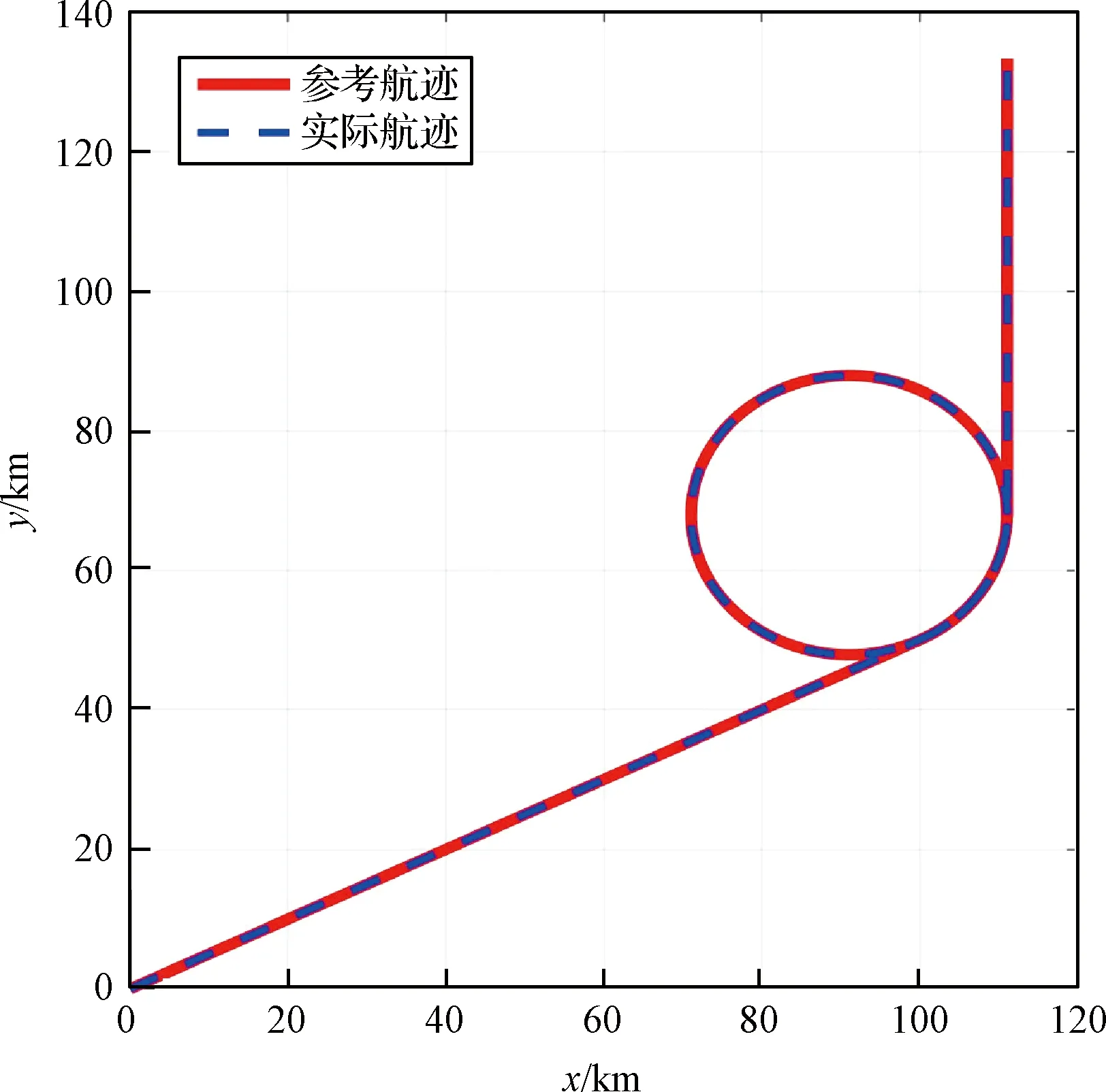
图6 控制增益动态优化时的轨迹跟踪结果Fig.6 Trajectory tracking results with dynamic optimization of control gain

图7 控制增益动态优化时的圆轨迹跟踪放大结果Fig.7 Amplification results of circular trajectory tracking with optimal gain

图8 控制增益动态优化时的轨迹跟踪误差Fig.8 Trajectory tracking error with optimal gain

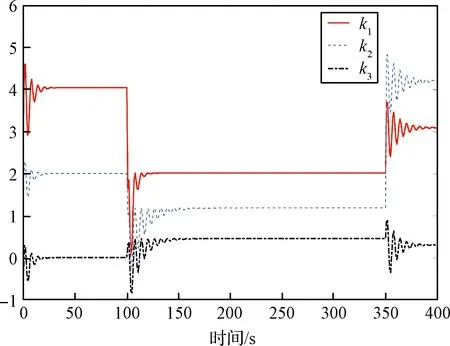
图9 控制增益参数变化过程Fig.9 Changing process of control gain

从图6～图8可以看出，采用神经网络动态优化增益参数后，在变化的扰动风场中，平流层飞艇实现了对参考轨迹的精确跟踪，轨迹跟踪误差仅在轨迹形式发生较大变化时有较大误差(0.7 km)，整体上误差维持在米量级且十分稳定，表明控制方法对外部扰动风场具有较好的鲁棒性。

由图9可知，采用RBF局部神经网络对三个增益参数进行动态寻优，能够快速收敛得到当前状态下的最优数值。

将利用RBF神经网络动态优化控制增益的方法，进一步应用于平流层飞艇模型参数不确定的情况。假设飞艇的转动惯量在±5%范围内随机波动，轨迹跟踪结果和跟踪误差如图10～图12所示，增益参数变化过程如图13所示。

从图10～图12可以看出，在系统模型参数不确定情况下，采用神经网络动态优化增益参数的方法，虽然误差存在一定震荡波动，但整体上误差值很小，除在轨迹切换处达到1 km左右外，实际轨迹与参考航迹的误差仍能控制在几十米范围内，表明轨迹控制方法具有较好鲁棒性。

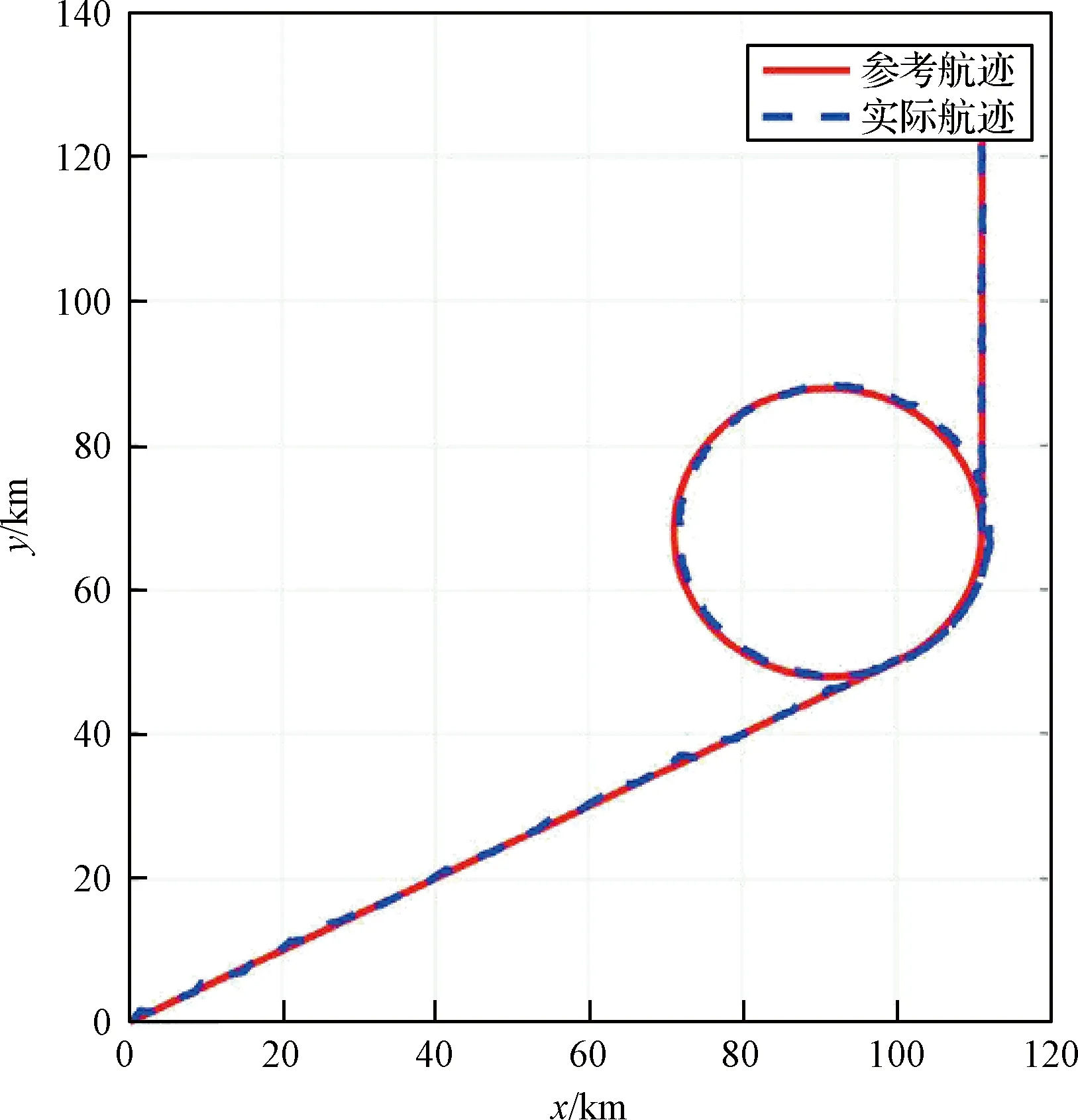
图10 模型参数不确定条件下的轨迹跟踪结果Fig.10 Trajectory tracking results under model uncertainty

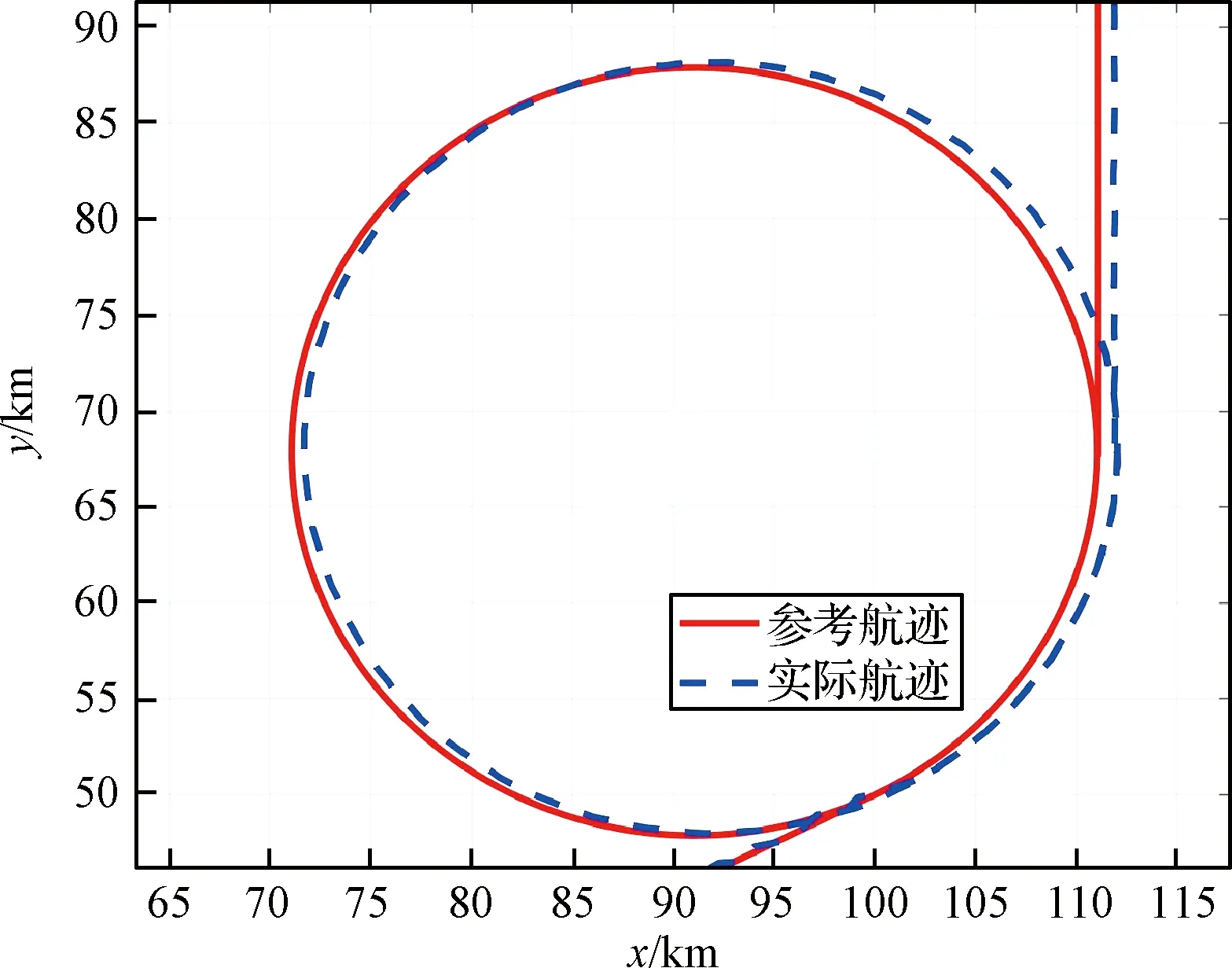
图11 模型参数不确定条件下圆轨迹跟踪放大结果Fig.11 The amplification results of circular trajectory tracking under model uncertainty

图12 模型参数不确定条件下轨迹跟踪误差Fig.12 Trajectory tracking error under model uncertainty

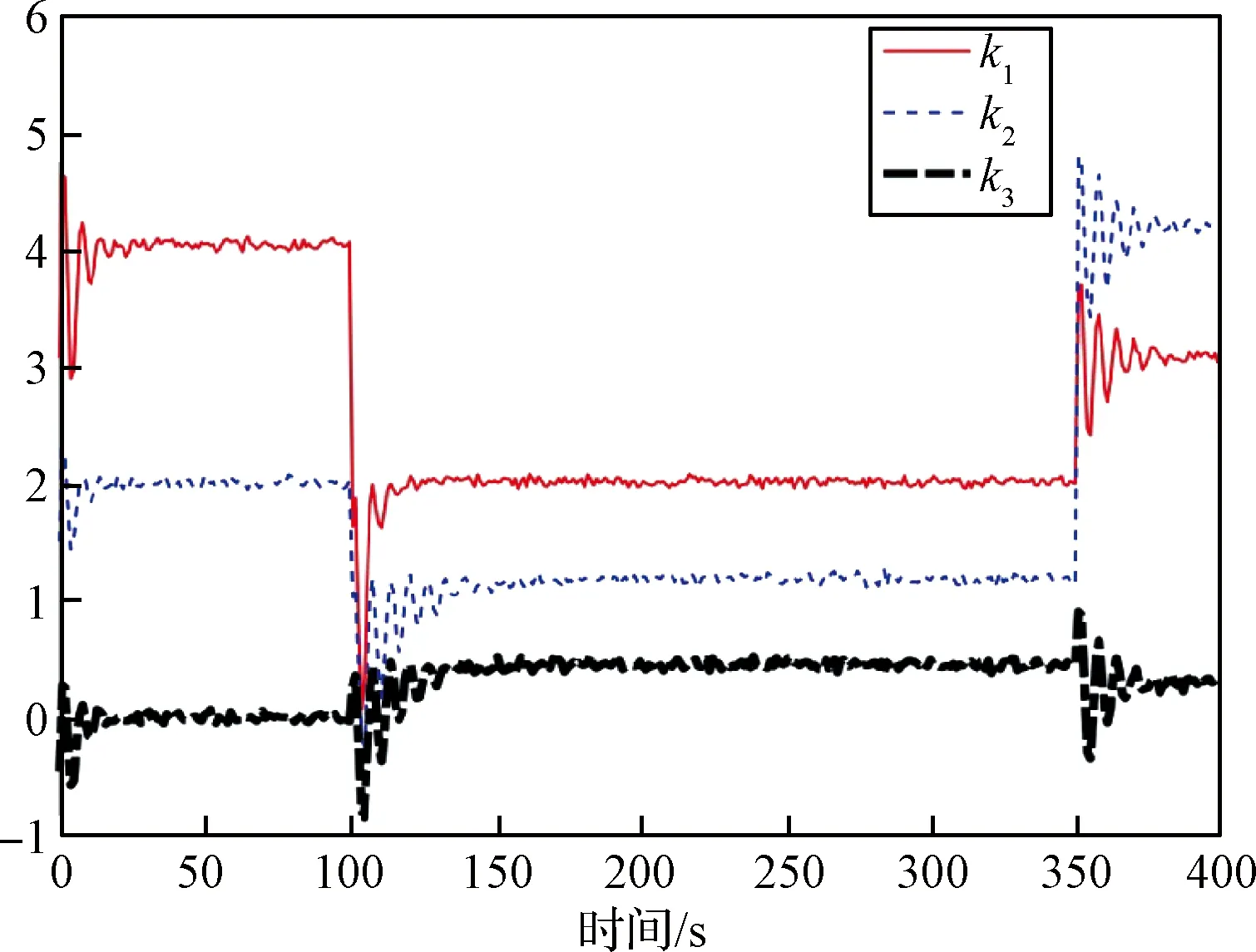
图13 模型参数不确定条件下控制增益参数变化过程Fig.13 Changing process of control gain under model uncertainty

仿真结果与文献[14]采用指数趋近律形式滑模控制环节的反步法控制器相比，风场扰动条件下，本文所提控制方法与其控制误差相当，模型不确定条件文献[14]仿真过程未考虑，且本文所提方法采用神经网络在线动态调整控制增益，智能自主程度高。

4 结 论

对于外部风场扰动和模型不确定条件下的平流层飞艇轨迹控制问题，采用反步法设计控制器，增益参数选取是关键和难点，本文提出采用RBF神经网络动态调整增益参数的方法，按照两个方法融合形成的水平轨迹跟踪控制器，可以高精度跟踪参考轨迹，鲁棒性、适应性好。文中给出的仿真实例说明了该方法的有效性。