大型空间电站在轨展开与组装动力学与控制

2021-03-31荣吉利石文静李伟杰辛鹏飞

宇航学报 2021年3期

荣吉利，崔硕，石文静，李伟杰，李潇，辛鹏飞,3

(1. 北京理工大学宇航学院，北京100081；2. 北京空间飞行器总体设计部，北京100094；3. 空间智能机器人系统技术与应用北京市重点实验室，北京100094)

0 引言

近年来中国航天发展迅速，对大型空间结构的研究越来越迫切，例如深空探测航天器大型太阳帆、空间站的太阳能阵列、大型在轨组装电站、大型空间模块化天线、大型载人空间站等。一系列大型空间站的研发逐渐提上日程。大型在轨组装电站由于结构巨大、尺度巨大、构建规模庞大，需要结构单元在折叠状态发射，后在空间轨道进行结构展开与组装，工况复杂，地面试验很难满足需求，因此采用准确有效的数值模拟方法预测空间结构动力学行为是设计的重要一环。文献[1]提出了一种热-力学耦合分析有限元方法，以解决大型空间结构的热变形问题。文献[2-3]对空间结构及在轨操作领域进行了多层次的深入研究。文献[4]对网架式星载天线非线性动力学与控制进行研究。文献[5]以太阳帆塔等细长结构中空间柔性梁为研究对象进行了稳定性分析。文献[6]提出了一种空间太阳能电站追踪太阳运动的准对日定向姿态方案。文献[7]提出了基于混合坐标法的太阳电池翼在轨载荷分析方法。美日等国早在多年前便开始研究空间太阳能发电技术，国内针对大型空间电站的研究依然存在大量空白。

受火箭运输能力制约，大型空间电站以可展开、可组装结构为结构单元，通常由大量梁、杆、薄板等柔性构件组成，且由于其尺度巨大，表现出大柔性、大变形的特点，是典型的刚柔多体系统。大多数商业软件无法有效处理大变形问题，因此自编软件成为解决这类问题的重要思路。采用精确的能解决大变形问题的刚柔耦合模型对研究空间电站展开与组装过程中动力学特性具有十分重要的意义。

此外，由于大型空间电站规模庞大，仿真计算量巨大，商业软件很难满足计算效率上的需求，在自编软件中嵌入高效的并行算法能显著提高计算效率，但本文暂不涉及并行算法相关内容。

多体系统动力学包含多刚体系统动力学和柔性多体系统动力学两类。文献[8-9]提出多刚体系统建模的自然坐标方法(Natural coordinate formulation, NCF)，又称为完全笛卡尔坐标法，该方法具有质量矩阵为常数矩阵，并且约束表示简单清晰等优势。

针对柔性多体系统动力学，文献[10]提出了浮动坐标法，又称为混合坐标法，是目前应用最广泛的柔性多体系统动力学分析方法。但是该方法仅仅适用于小变形问题，不能精确地描述柔性构件大变形。文献[11-12]提出了能够精确描述柔性构件大变形的绝对节点坐标方法(Absolute nodal coordinate formulation, ANCF)，采用斜率矢量代替了传统有限元中的转角坐标，将单元的节点坐标全部定义在全局坐标系下，不存在小变形、小转动假设，所推导的多体系统微分代数方程具有常数质量矩阵，不存在科氏力和离心力项，能够精确描述大变形问题。由NCF和ANCF共同搭建的刚柔耦合多体系统动力学方法称为绝对坐标[13-15](Absolute coordinate-based method, ACB)方法。

本文针对某典型百米尺度高刚度桁架类大型空间电站在轨展开与组装过程中的动力学特性进行研究，采用NCF与ANCF建立可适用于模型大变形的刚柔耦合模型，开发了一套动力学仿真软件，并采用商业软件MSC.ADAMS与ANSYS联合仿真[16-17]验证其在小变形下仿真模型的准确性，且由于所采用建模方法中不存在小变形、小转动假设，优于大多数商业软件，可适用于结构大变形、大转动动力学预测；针对线形桁架多级展开过程的结构振动问题选定了运动规划方案，能有效抑制结构振动，增强展开过程稳定性；探究了组装过程中组装速度、组装机构劲度系数与阻尼系数对组装过程稳定性的影响，并提出了对参数设计的优化思路；集成了一套针对大型空间电站的动力学仿真平台搭建方法，可为进一步开展此类大型空间结构的设计与研发工作提供有力的技术支持与方法指导。

1 大型空间电站及其建模

1.1 大型空间电站构建方案

针对大型空间结构的构建方法[18]大致分为三类：可展开结构构建、太空成形结构构建以及可直立结构构建。三类方法各有其优缺点。

可展开结构构建将折叠结构在地面组装，后经火箭等发射进入轨道，在轨道中逐级展开，这种方案减少了在轨道中操作的工作量，但实现风险较大，容易出现结构无法完全展开的问题，可靠性较低。太空成形结构构建方法，主要是将未加工的材料，在轨道成形装配。可直立结构构建将大型空间结构的部件在地面搭建，逐个发射后在空间中进行组装。

本文作为研究对象的典型大型空间电站，其构建方案结合了可展开结构构建与可直立结构构建，将部件在地面折叠后集中发射，进入轨道后进行部件展开与组装，能有效提高构建效率。但是大型空间电站在轨展开与组装过程过于复杂，将大大增加构建难度。因此这种方案更适用于由同类或少数几类部件构建的大型空间结构，有利于减小在轨操作的风险和难度。

电站结构的部件构型参考专利：“一种可重复展收的桁架结构及其胞元”[19]。根据专利设计，整个大型空间电站可以通过两类基础桁架胞元构建而成。构建过程大致可分为：1)单个胞元结构折叠并集中发射；2)在轨道中单个胞元的展开；3)胞元组装成为空间电站中心体结构；4)胞元多级展开；5)带太阳翼的线形桁架向中心体的组装；6)辐射桁架的展开与组装；7)环形桁架的展开组装；8)多级带太阳翼桁架向空间电站的组装等。

1.2 建模方法

本文所研究的大型空间电站包含大量柔性与刚性构件，是典型的刚柔多体系统，选择采用自然坐标方法与绝对节点坐标方法对其建模，可以精确描述大型空间结构在构建过程中的大变形、大转动。

1.2.1自然坐标法

自然坐标法中选取刚体上2个固定点的位置矢量与2个单位矢量作为广义坐标，见式(1)，包含12个自由度：

(1)

式中:ri,rj为刚体上固定点i,j的位置矢量，u和v为刚体上固定的单位矢量。以点i为局部坐标系原点，以(rj-ri),u,v为局部坐标系的基矢量构建刚体局部坐标系ξ-η-ζ如图1所示：

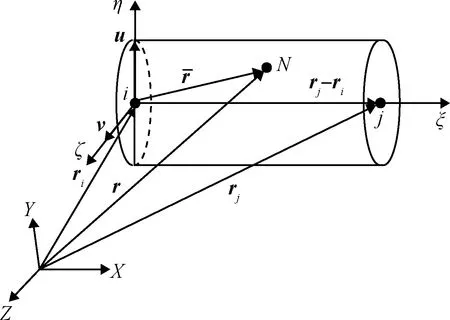
图1 NCF描述的空间刚性体Fig.1 Spatial rigid body described by NCF

刚体上任意一点N在局部坐标系ξ-η-ζ下的位置矢量为：

(2)

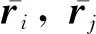
(3)

刚体上任意一点N在全局坐标下的位置矢量可表示为：

r=(1-c1)ri+c1rj+c2u+c3v

(4)

将式(4)改写成如下矩阵形式：

(5)

式中:C=[(1-c1)I3,c1I3,c2I3,c3I3]，称为形函数，I3是3阶单位矩阵。

1.2.2绝对节点坐标方法

采用ANCF全参数梁单元对结构中的柔性杆建模，如图2所示。

图2 ANCF描述的全参数梁单元Fig.2 Full-parameter beam element described by ANCF

该单元中任意一点N的全局位置矢量为：

r=[r1,r2,r3]T

(6)

e为单元的广义坐标，定义如下：

(7)

通过有限元理论形函数的一般推导方法，可得到该单元的形函数S为：

[s1I3,ls2I3,ls3I3,ls4I3,s5I3,ls6I3,ls7I3,ls8I3]

(8)

式中:I3为3×3单位矩阵；s1=1-3ξ2+2ξ3，s2=ξ-2ξ2+ξ3，s3=η-ξη，s4=ζ-ξζ，s5=3ξ2-2ξ3，s6=-ξ2+ξ3，s7=ξη，s8=ξζ，其中，ξ=x/l，η=y/l，ζ=z/l，l为单元长度。

ANCF全参数梁单元上任意一点N的全局坐标均可表示为：

r=Se

(9)

将式(9)对时间求导，可得到：

(10)

进而可得到单元的动能为：

(11)

单元的质量矩阵为：

(12)

式中：ρ表示密度，V为体积积分变量，Ve为体积积分域，M为常数质量矩阵。

1.3 滑移铰建模与仿真校验

桁架类空间结构展开过程中伴随滑移铰的滑移，在动力学仿真中涉及节点沿单元的移动，会导致约束方程的改变，因此对滑移铰的精确建模十分关键。

1.3.1滑移铰建模方法

文献[20]提出了一种滑动关节建模方法，采用4个约束方程公式化滑移铰。

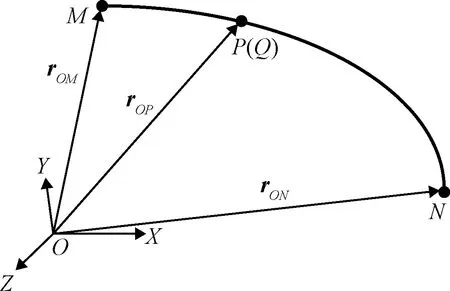
图3 滑移铰Fig.3 Sliding joint

如图1所示，滑动关节在主体上的P，以及在滑动杆上的未变形的局部相对位置Q，ξt为t时刻点P相对于MN的物质坐标，满足ξt=lMP/lMN。由式(13)：

rOQ=S(ξ,η,ζ)eMN

(13)

滑移铰所需要的满足的约束方程如下：

(14)

在式(14)中，第一行的等式包含3个约束，第二行包含1个约束。前3个约束用于将点P与Q的运动限制在相同的全局位置，这导致对应生成三个拉格朗日乘子λ=[λ1,λ2,λ3]T。滑移铰在没有摩擦力的情况下，约束力仅存在于垂直滑动方向上，在滑动方向上无约束力，即为第4个约束的含义。

在ANCF全参数梁单元中，有：

(15)

式中：sx1=-6ξ+6ξ2，sx2=l(1-4ξ+3ξ2)，sx3=-lη，sx4=-lζ，sx5=6ξ-6ξ2，sx6=l(-2ξ+3ξ2)，sx7=lξ，sx8=lζ，其中，ξ=ξt，η=y/l，ζ=z/l，l为单元长度。

1.3.2带滑移铰的展开动力学仿真校验

建立带滑移铰的单个胞元展开动力学模型，结构构型参考专利：“一种可重复展收的桁架结构及其胞元”[19]。

根据专利内容，单胞元结构为单自由度结构。采用ANCF全参数梁单元对柔性杆进行离散；锁定机构与其位于的刚性框之间建立滑移铰约束；各杆之间建立旋转铰约束。

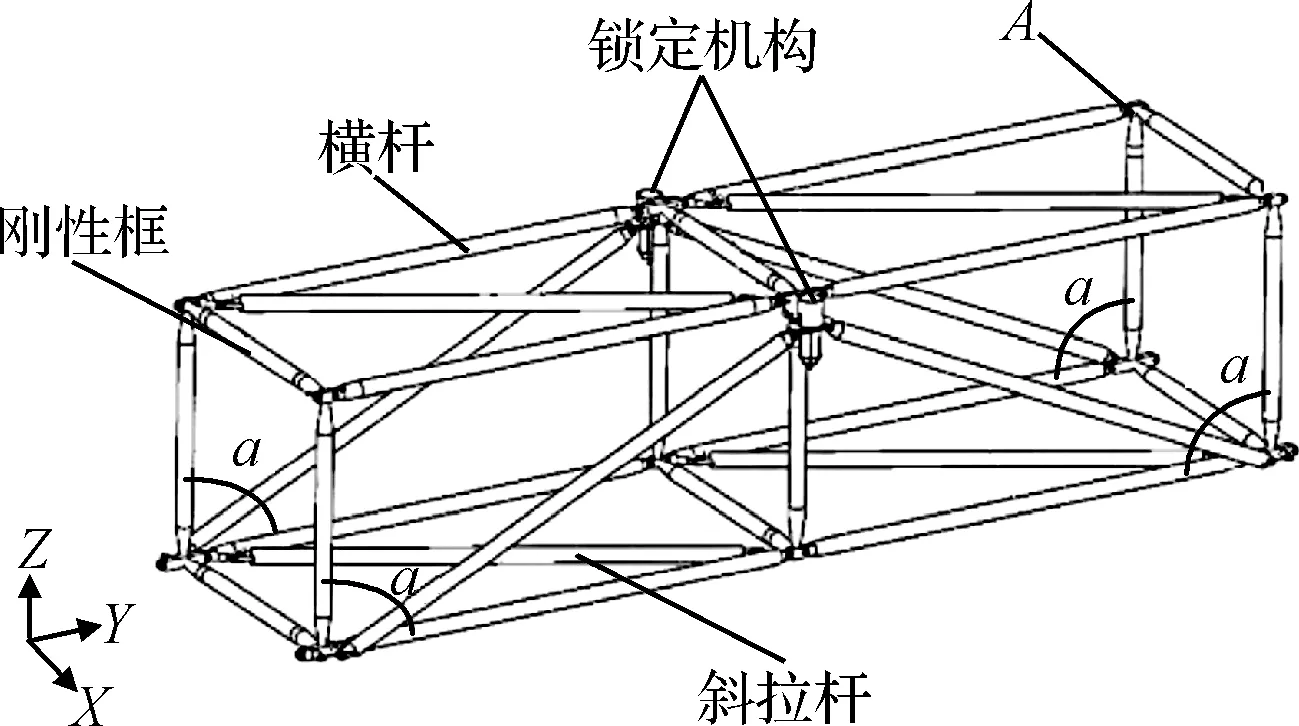
图4 单个胞元结构示意图Fig.4 Single cell structure diagram

各项参数见表1：

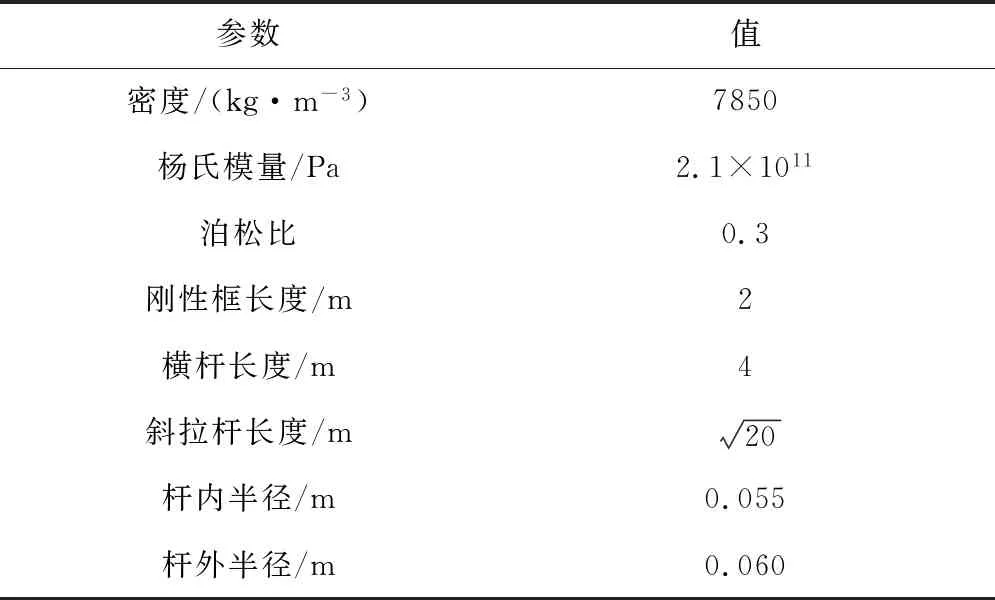
表1 结构参数Table 1 Structural parameters

α0=5°为折叠状态初始角度，αf=90°为完全展开时目标角度。

固定胞元一端的刚性框，连杆间交接方式为旋转铰接；在胞元上施加沿Y正方向大小为0.005g的重力加速度。

由于模型中单个胞元展开过程所施加载荷较小，因此柔性与变形较小，商业软件能够有效处理此类问题，选择采用MSC.ADAMS与ANSYS联合仿真方法[16-17]。首先在MSC.ADAMS中建立单个胞元模型，在ANSYS中生成模态中性文件(.mnf文件)后导入ADAMS/FLEX模块，可实现基于模态频率对柔性件的建模与仿真。

绘制A点Y坐标变化曲线图如图5所示：

图5 A点Y坐标变化曲线图Fig.5 The Y-position of point A

本文建模方法的结果与商业软件MSC.ADAMS与ANSYS联合仿真结果基本一致，验证了所建立约束尤其是滑移铰的准确性，同时验证了基于NCF与ANCF建立的动力学模型的准确性。

相较于商业软件MSC.ADAMS与ANSYS联合仿真方法，本文建模方法在处理柔性体尤其是大变形问题时更加精确。对比重力加速度为0.05g、0.5g、1g、10g的情况下两种仿真方法的结果如图6所示，分别以“G0.05”、“G0.5”、“G1”、“G10”代指对应载荷工况。

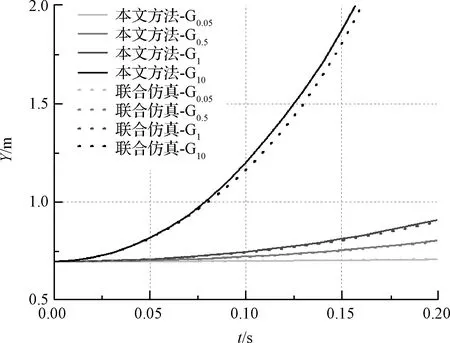
图6 A点Y坐标变化曲线图Fig.6 The Y-position of point A

表2选取0.05 s、0.10 s、0.15 s、0.20 s对比不同载荷情况下商业软件相较于本文方法结果之间的误差。随载荷增大，两种方法之间误差逐渐增大。当载荷较大时，结构出现较大变形，商业软件MSC.ADAMS与ANSYS联合仿真结果出现较大误差。本文建模方法不存在小变形、小转动假设，在求解柔性体变形问题中更加精确，这一大优势使之更适用于有大柔性、大变形特点的大型空间电站的动力学行为论证。

表2 误差对比Table 2 Error comparison

2 大型空间电站构建过程中典型工况

大型空间电站构建过程复杂，构建方案与构建方式多样，且涉及不同的环境扰动等影响因素，自编软件可以适用于整个大型空间电站的构建过程，本文以某典型桁架类大型空间电站系统为研究对象，选取结构展开与组装过程中的两类典型工况进行分析。

2.1 线形桁架展开规划

由于火箭单次运输空间有限，空间电站的结构胞元需要在折叠状态下运输至太空轨道，后在轨道中进行展开与组装操作，因此针对结构在空间中展开过程进行的动力学仿真尤为关键。

胞元展开控制方式对结构稳定性影响很大，良好的展开控制方案能有效抑制结构振动。

针对图4中单个胞元的展开过程，选用5种角度控制函数如下，分别为线性函数、三次多项式插值函数、五次多项式插值函数、摆线运动插值函数以及余弦插值函数：

(16)

(17)

(18)

(19)

(20)

式中:α如图4所示。α0=5°为折叠状态初始角度，αf=90°为完全展开角度，tf=10 s为单个胞元展开时间。

由于不同的工况中所选取的样点初始空间坐标会有区别，以下统一选择位移曲线而非坐标曲线进行对比分析。

图7～9中，SX,SY,SZ分别表示X,Y,Z方向的位移。

由图7可知，线性函数的结果有明显的振动，这是由于线性函数的初始增量太大，结构产生较大的弹性变形，导致展开过程不平滑。其它4种控制函数在Y方向上位移曲线光滑。由于初始状态单个胞元存在α0=5°，A点Y坐标初始值为0.6972 m，故图7中Y方向位移平衡值为7.3028 m。由图8和图9可知，余弦插值函数有最好的展开稳定性与最小的振动残留，但是位移峰值大于摆线运动插值函数。摆线运动插值函数稳定性与振动残留仅次于余弦插值函数。

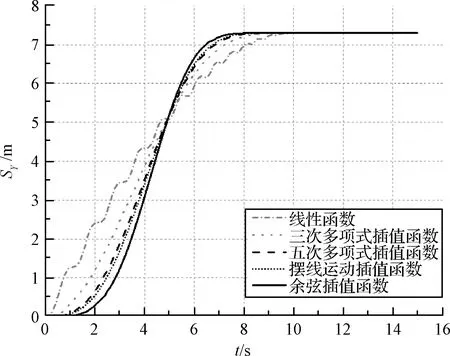
图7 不同的角度控制函数下A点Y方向位移曲线图Fig.7 The Y-displacement of point A from different angle control functions

图8 不同的角度控制函数下A点X方向位移曲线图Fig.8 The X-displacement of point A from different angle control functions

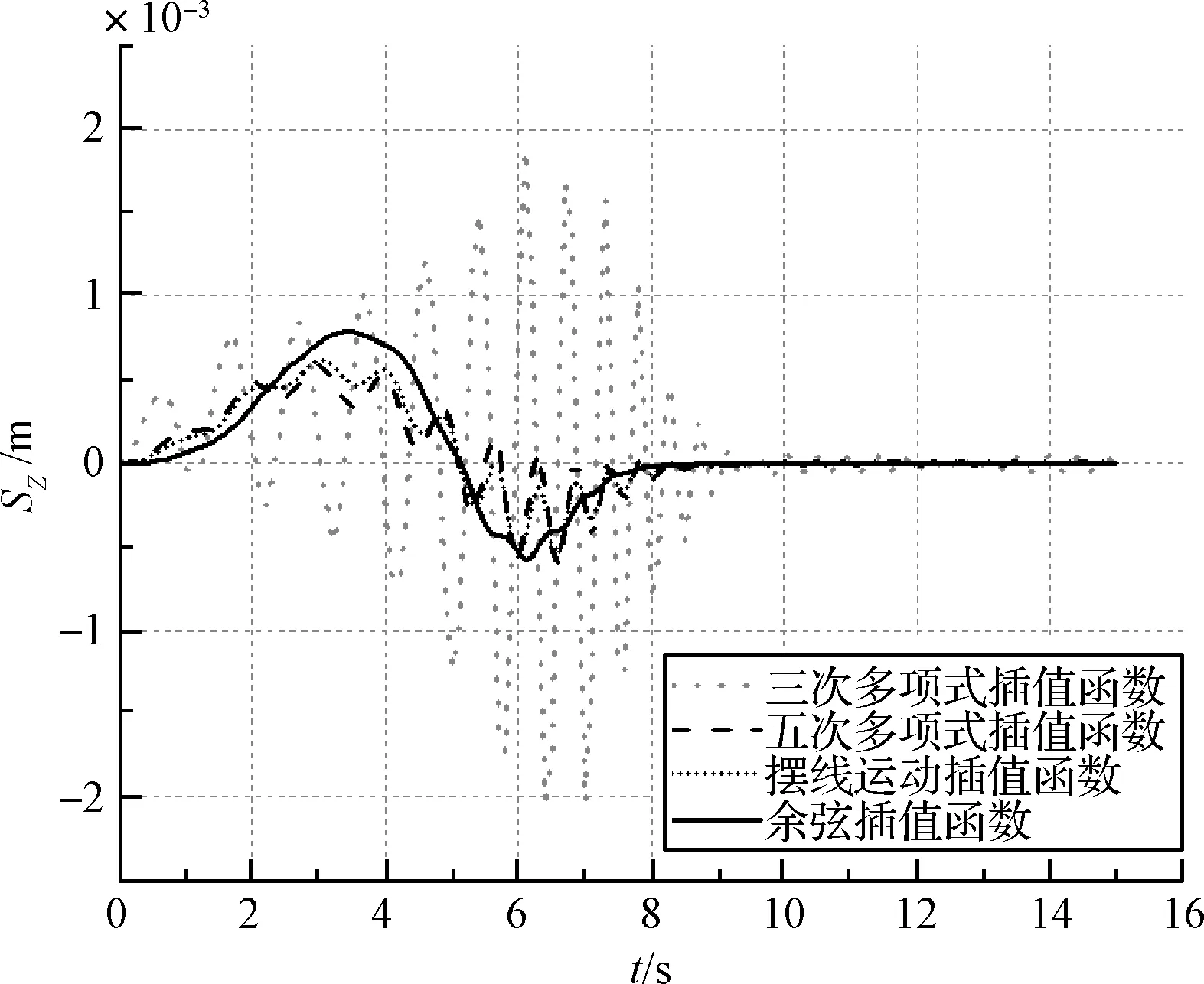
图9 不同的角度控制函数下A点Z方向位移曲线图Fig.9 The Z-displacement of point A from different angle control functions

针对包含8个胞元的折叠结构多级展开过程，分别选用摆线运动插值函数与余弦插值函数作为角度控制函数。

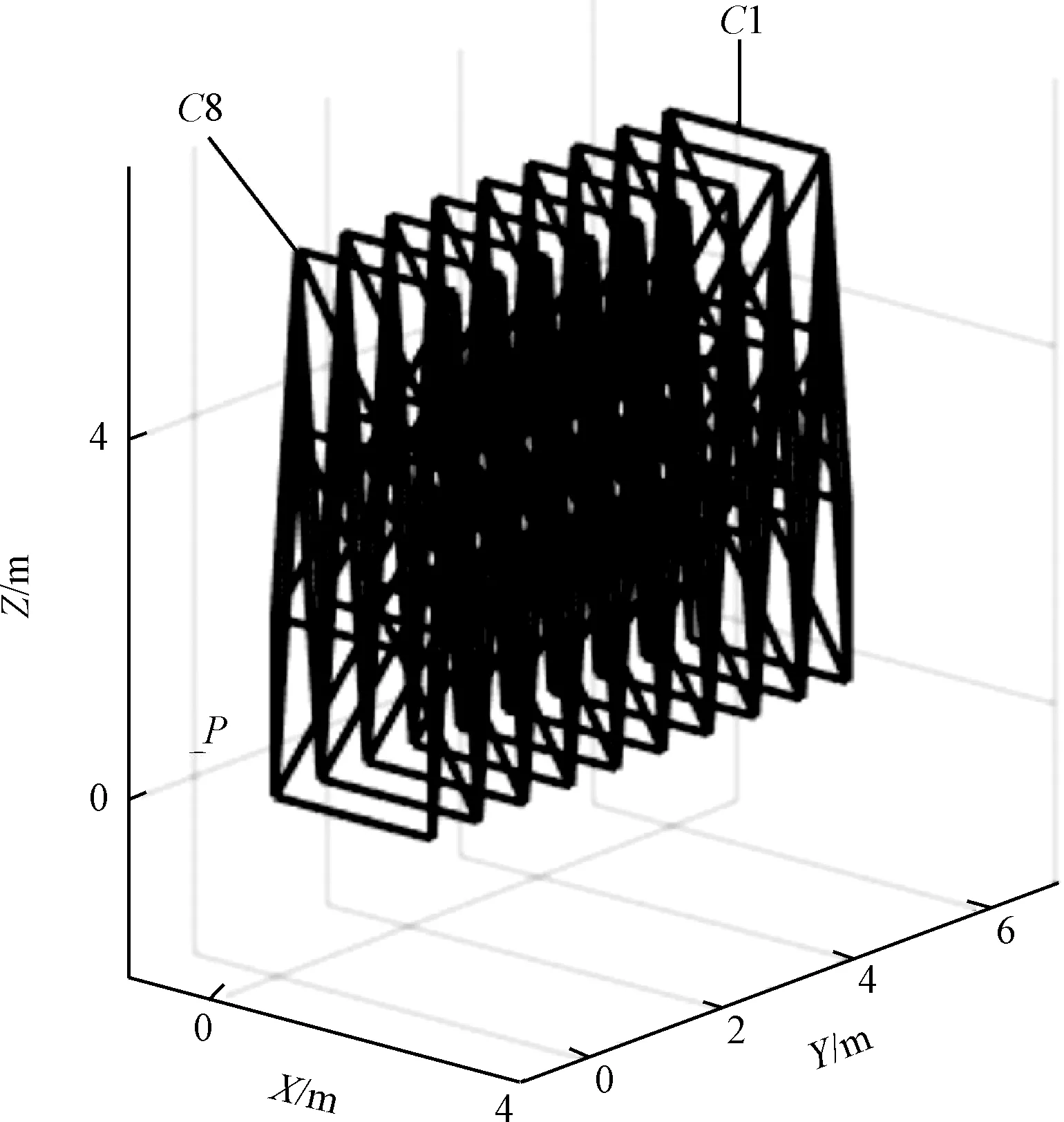
图10 8个胞元折叠状态图Fig.10 8 cells folded state diagram

从远离固定端P的胞元C1逐级沿Y方向展开，参数与单胞元一致，相邻胞元的展开开始时间间隔12 s。在胞元C1上对应图4中A点。

图11 不同的角度控制函数下A点Y方向位移曲线图Fig.11 The Y-displacement of point A from different angle control functions

图12 不同的角度控制函数下A点X方向位移曲线图Fig.12 The X-displacement of point A from different angle control functions

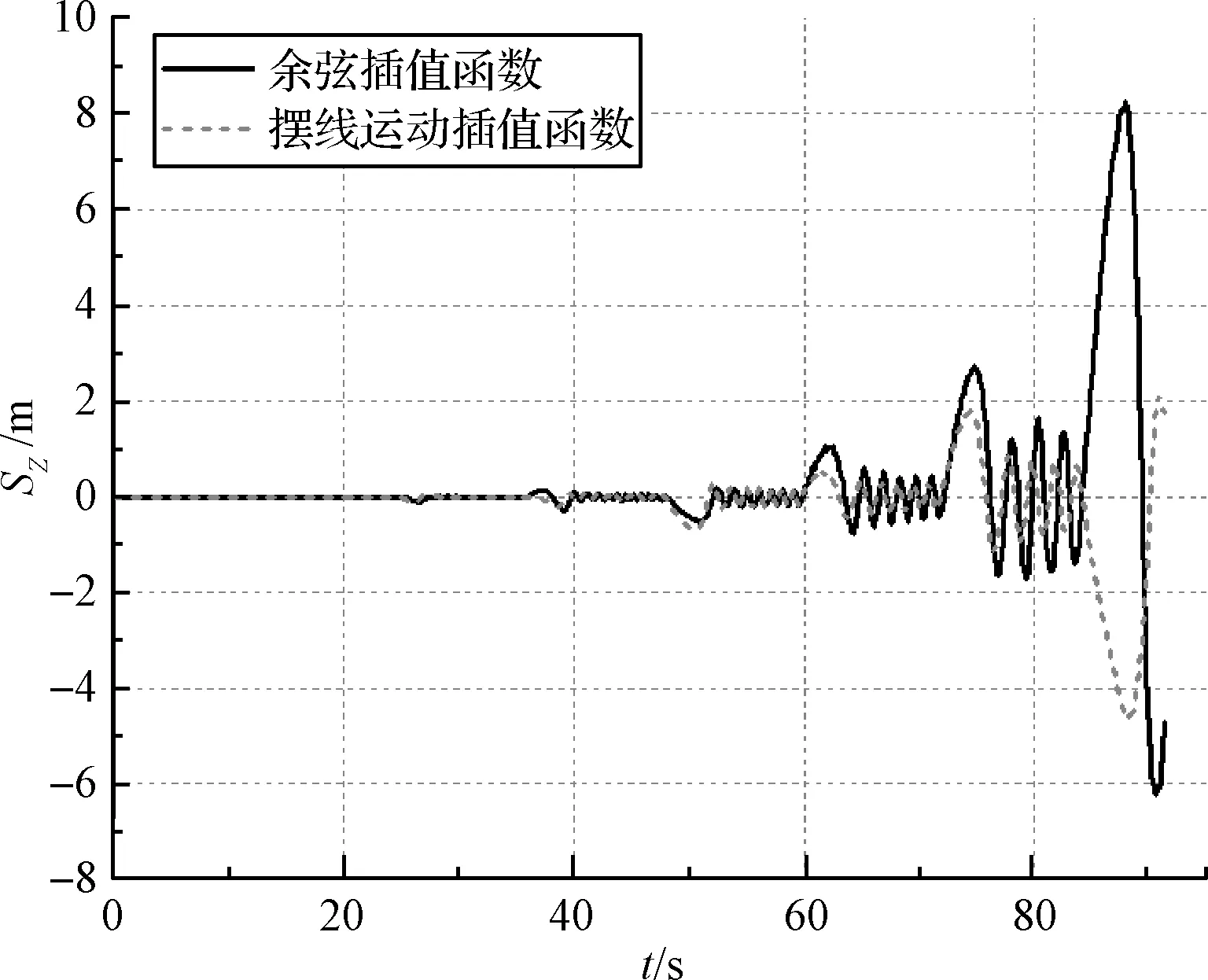
图13 不同的角度控制函数下A点Z方向位移曲线图Fig.13 The Z-displacement of point A from different angle control functions

结构展开沿Y方向。由图11可知Y坐标变化有明显的阶段性，摆线运动插值函数与余弦插值函数都具有良好的稳定性。

由图12和图13可知，随着结构多级展开，采用余弦插值函数作为角度控制函数时结构振动更明显，在第7个胞元展开后X方向最大位移为4.402 m，Z方向最大位移达到8.253 m，而采用摆线运动插值函数在X方向最大位移为0.363 m，Z方向最大位移为4.577 m。由此得出结论，在桁架结构多级展开中，摆线运动插值函数明显优于余弦插值函数。

2.2 线形桁架向中心体的组装

结构在轨展开后，需通过组装的方式逐步拼接构建成完整结构。

大型空间电站采用先组装中心体结构，后组装外围结构的方式逐步搭建。对带太阳翼的线形桁架向中心体结构的组装过程进行动力学仿真。

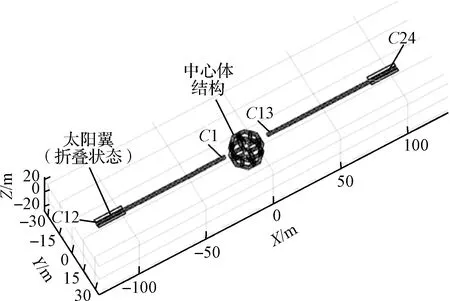
图14 线形桁架向中心体组装Fig.14 Linear truss assembly to center body

模型如图14所示。X正轴与负轴方向上两个被组装的线形桁架长度为96 m，各包含12个线形胞元。组装过程中太阳翼处于折叠收拢状态，折叠状态刚度较大，在空间电站组装过程中无需考虑其柔性，故采用NCF方法建模。单个太阳翼质量为2 t。

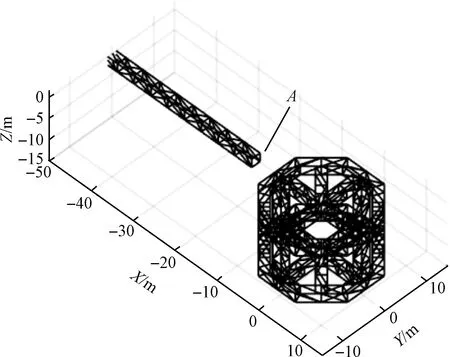
图15 组装局部图Fig.15 Partial assembly diagram

选取一组组装参数见表3，作为对照参数,建立3个对比算例，分别改变组装速度v、组装机构劲度系数K以及组装机构阻尼C，对比不同组装参数对组装过程稳定性的影响。

表3 参数Table 3 Parameters

由于在Y，Z方向上位移变化小于10-5m，组装机构内力小于1 N，相较于X方向可以忽略，因此仅对比X方向上位移与内力变化。绘制组装过程中A点在X方向(为组装方向)上的位移曲线与组装机构内力变化曲线图如图16～17所示。

图16 组装过程中A点X方向位移曲线图Fig.16 The X-displacement of point A during structure assembly

图17 组装过程中组装机构内力曲线图Fig.17 Internal force curve of assembly mechanism during structure assembly

由图16～17，采用表3参数时，在t=6.1705 s时点A距离平衡位置最远，为0.10303 m，t=5.6305 s时组装机构内力出现最大值，为246 N；当v=0.5 m/s时，在t=3.161 s点A距离平衡位置最远，为0.27628 m，在2.611 s时内力峰值为660.5 N；当组装机构阻尼系数C=500 N·m-1·s-1，在t=6.2505 s时，点A位移最大值0.13453 m，在t=5.9905 s时，内力峰值280 N，达到平衡状态所需要的时间大大增长;组装机构劲度系数K=1500 N/m时,在t=6.3205 s，点A距离平衡位置位移最大值0.11178 m，当t=5.5905 s时内力最大值213.6 N。当组装速度增大时，组装过程发生得更早，但组装过程位移更大，内力也明显增大；当减小C时，位移峰值与内力峰值会增大，但峰值发生时间会延后；当减小K时，位移峰值增大，内力峰值略微减小。

通过以上结果给出优化方案，为使组装过程更加稳定，应该减小组装速度v，增大阻尼系数C，适当增大机构劲度系数K。