面向中末交接班的临近空间拦截弹弹道优化

2021-03-31李为民王华吉雷虎民

宇航学报 2021年3期

张涛，李为民，李炯，王华吉，雷虎民

(1.空军工程大学防空反导学院，西安 710051；2.中国人民解放军 94011部队,和田 848000)

0 引言

临近空间高超声速武器是以高超声速飞行器为载体或直接作为武器本体使用，长时间在临近空间飞行的武器，具有作战空域大、飞行速度快、突防能力强、毁伤范围广等特点[1-2]。近年来美军先进高超声速武器已进入型号研发阶段，而俄罗斯的空射型高超声速导弹“匕首”和“锆石”近日也进行飞行试验和战斗值班任务。为有效应对临近空间高超声速武器构成的严峻威胁，发展反此类目标的先进拦截技术和防御手段已迫在眉睫。

拦截弹中制导是防御作战中飞行距离最长的一个阶段，中制导弹道的优劣将直接决定拦截的成败。拦截弹中制导弹道优化问题属于非线性、带有状态约束和控制量约束的最优控制问题[3-4]。文献[5]考虑弹道过程约束，以末速最大、终端点距离误差最小和全程热量最小为指标建立拦截弹弹道规划问题，为高超声速目标拦截弹中制导问题奠定了基础，然而并未考虑中末制导交接班条件的约束。

零控拦截流型是拦截弹中制导终端时刻的最优拦截几何，拦截弹可在无控状态下在有限时间内实现对目标的拦截。根据高超声速目标的特性和临近空间的环境特点，考虑到拦截弹自身携带的燃料以及气动力所提供的过载有限，拦截弹在中制导阶段需要进入或者接近这个最优的拦截几何。

文献[6]首先完整地描述了零控拦截交班区域，采用模型预测静态规划理论设计了单枚拦截弹考虑零控交班约束的中制导律，该方法不仅能精确覆盖交班区域，还可以满足位置、角度以及导引头特性等终端约束；文献[7]提出一种面向零控交接班区域的有限时间一致收敛的协同中制导方法，能够保证多枚拦截弹在有限时间内同时到达所指定的零控交接班区域，然而都没有考虑拦截弹热流、动压、过载等约束条件对中末制导交接班的影响。

此外，拦截弹飞行速度可达到马赫数10，强烈的气动加热会严重影响拦截弹导引头的探测精度，因此需要将导引头安装在拦截弹的侧面来避开导弹头部的热流密集区，这种侧窗探测技术将会导致视线不对称，从而使拦截弹在弹道设计和姿态控制过程中会收到一定的约束和限制[8-9]。然而当前关于中制导弹道优化及中末制导交接班窗口的描述中，均未考虑侧窗探测对中制导弹道优化的影响[10-12]。

面向中末制导交接班的拦截弹中制导弹道优化属于非光滑轨迹优化问题[13]，目前解决该问题的优化方法有直接法和间接法两大类。虽然间接法具有坚实的理论基础，但由于它对初值敏感且收敛半径小，求解过程比较复杂，不适用与弹道优化问题的求解。直接法中的配点法由于不需要推导最优性必要条件，并且对优化初值的敏感性较低，容易收敛，再加上计算机技术和相关理论的发展，直接法逐渐成为弹道优化领域的研究热点。直接配点法通过对控制变量和状态变量都进行离散，将轨迹优化问题转化为非线性规划(Nonlinear programming, NLP)问题。

传统配点法在求解非光滑最优控制问题时存在网格和配点数目多、非线性方程计算量大、误差大等问题。因此需要根据最优控制问题的光滑程度对网格进行优化。网格优化主要的问题是网格划分的位置、子网格和网格内配点的数量。文献[14]提出了一种分段hp自适应网格细化方法，该方法根据离散误差值来分辨分段点的位置以及网格内的配点数，然而并未给出网格划分的理论依据。文献[15]针对高超声速再入飞行器的轨迹优化问题，根据飞行器轨迹的曲率作为选择h法或者p法的依据，通过增加插值多项式维数或细化网格的方式提高解的精度。文献[16]给出离散误差的估计公式来确定非光滑区域的位置，构造自适应网格更新策略，使节点能够根据离散误差的大小自动调整。文献[17]研究了自适应Radau伪谱法的网格缩减算法，仿真结果表明采用网格缩减算法能够降低转化后的NLP问题的维度，提高求解效率，利于拦截弹轨迹的高精度、快速优化求解。因此，论文将考虑用hp自适应网格细化技术求解优化弹道。

为了能够适应临近空间防御作战的特点，本文以高抛再入式迎面拦截高超声速目标为背景，考虑热流、动压、过载、侧窗探测等约束，设计了面向中末制导交接班的临近空间拦截弹弹道。论文的主要创新工作有：1)提出了能量受限的侧窗探测拦截弹中末制导交接班窗口，为拦截弹提供完备且可靠的中末制导交接班终端约束条件；2)针对拦截弹交接班过程会受到气动热的影响，文中提出了导引头侧窗背风探测的交接班方案；3)将中末制导交接班窗口的拦截弹中制导段弹道优化问题转化为NLP问题，设计了hp自适应网格优化算法求解非光滑轨迹优化问题。

1 问题描述

1.1 拦截弹纵向平面运动模型

本文考虑拦截弹从再入点到交接班点的弹道优化问题，此过程推力发动机已被抛掉，即推力为零。拦截弹纵向平面内的质点运动模型为：

(1)

式中:VM与θM分别表示拦截弹速度和弹道倾角，xM，yM分别为导弹在大地惯性坐标系下的位置，q表示动压，S表示参考面积，g表示重力加速度，θM为弹道倾角，m为拦截弹质量，Cx，Cy分别为阻力系数以及升力系数，根据空气动力学知识，它们可以分别表示为攻角的函数为：

(2)

(3)

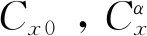
1.2 中制导弹道优化问题描述

拦截弹中制导弹道优化实际上是求解最优攻角α与设计终端时刻tf，同时使得由弹道方程组确定的系统在满足攻角、动压、过载、热流密度以及终端状态等约束条件下性能指标最优。

为了拓宽拦截弹可行的末制导初始条件以及保证拦截弹的杀伤效果，选择末端速度最大作为一个终端优化指标。即：

J=φ(VM(tf),tf)=-VMf

(4)

式中:tf表示终端时刻，

拦截弹中制导段弹道的终端约束条件为：

xMf=xMd,yMf=yMd,θMf=θMd

(5)

式中：xMd，yMd和θMd分别为终端期望射程、期望高度和期望弹道倾角，根据零控交接班条件可以获得(xMd,yMd,θMd)，通过控制拦截弹中制导弹道的终端状态满足此期望终端条件来完成中末制导交接班，而期望终端条件的描述将在下节介绍。

同时拦截弹弹道规划还需要满足如下过程不等式约束条件，为保证拦截弹飞行的稳定性，拦截弹攻角大小应满足：

(6)

动压极限值主要取决于热防护材料强度与气动控制铰链力矩。其约束设置为：

(7)

式中:ρ为空气密度。

在临近空间范围内，拦截弹所能提供的可用过载大小有限，故过载约束设置为：

(8)

考虑到拦截弹的热流密度约束，其简化计算公式为[19]：

(9)

2 能量受限的中末制导交接班窗口

2.1 中末制导交接班窗口

在对临近空间高超声速目标拦截时，由于目标飞行速度高且飞行环境复杂，为保证拦截弹正常飞行，需要考满足以下约束[20-21]：1)较小的能量消耗，为末制导拦截弹机动提供足够的能源储备；2)过载约束，防止结构性破坏；3)动压约束以及驻点热流约束，防止铰链力矩过大和热烧蚀；4)攻角约束，满足飞行器控制能力。此外，为保证中末交接班顺利完成，中末制导交接班还必须满足：1)特定的攻角与姿态角，以确保侧窗探测导引头对目标的有效捕获；2)较小的中末交接班误差，确保进入末制导能够形成较好的拦截流型；3)较大的拦截弹速度以确保末制导过程中拦截弹的机动性能以及战斗部的碰撞杀伤性能。文献[12]给出了拦截弹中末制导交接班窗口的定义，但并未考虑拦截弹能量约束和侧窗探测的影响。为了更完善地描述交接班约束条件，本文给出如下定义。

定义1.在拦截高超声速目标时，导弹中末制导交接班窗口为在满足侧窗探测导引头截获条件的基础上，同时满足末制导捕获状态空间的约束和能量约束，其中捕获状态空间由弹目相对距离矢量、拦截弹速度矢量以及目标速度矢量组成。

2.2 中末制导交接班窗口定量描述

中制导及交接班过程中的弹目运动学关系如图1所示，其中OXY为笛卡尔惯性参考系，R和λ分别表示弹目相对距离矢量和弹目视线角，VM和aM分别表示拦截弹的速度矢量和加速度矢量，VT和aT分别表示目标速度矢量和加速度矢量，ηM和ηT分别表示拦截弹和目标的前置角。根据PIP推导零控交班点(Zero effort handover point, ZEHP)，中制导的目的是控制拦截弹到达或者尽量接近零控交班点。弹目平面内运动学方程为

(10)

(11)

(12)

(13)

(14)

(15)

(16)

红外导引头截获目标后可以获得视线角速率信息，因此假设末制导段采用纯比例导引律(Pure proportional navigation guidance, PPN)控制拦截弹飞行目标，其表达式如下

(17)

式中：N代表导航系数。

图1 中制导阶段的弹目运动示意图Fig.1 The relative motion between interceptor and target through midcourse guidance

下面将通过引入3个引理来定量描述能量受限条件下的中末制导交接班窗口，并给出中末制导交接班窗口的计算步骤。

引理1[22].在不考虑拦截弹能量受限情况下，为顺利完成交接班，则交接班时刻拦截弹速度和目标速度与弹目视线的夹角应满足如下约束：

CPPN={(ηT,ηM)|(ηM)min≤ηM≤arcsinkc，

π-arcsin(kc/p)≤ηT≤π+ηc,

ηT≤π-arcsin(sin(ηM)/p),

ηT≥π-(ηM+μmax)/(N-1)}

(18)

则在PPN导引律控制下可以有限时间内使得R→0。其中，μ(k)=arcsink-(N-1)arcsin(k/p)，k为函数自变量，p=VT/VM，ηc=arcsin(1/p)。通过对μ(k)求导来获取极值，可得分段函数μmax如下：

(19)

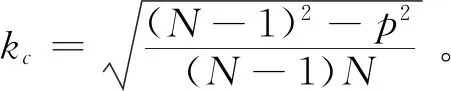
(20)

拦截弹中末制导交接班窗口计算步骤如下：

步骤1：根据目标运动速度和拦截弹自身速度的比值，以及导航比，按照公式计算捕获状态空间。

步骤2：通过对高超声速目标轨迹进行跟踪与预测，获得交接班时刻目标的速度指向和位置，由引理3计算拦截弹的零控交接班区域。其中，最优速度指向与弹目视线夹角为ηM=arcsin(psinηT)。

步骤3：通过目标与拦截弹的速度比以及导引头的最大探测范围，计算拦截弹位置与速度指向的允许范围。

步骤4：判断拦截弹是否满足引理2能量的约束，当轨迹预测误差超出了拦截弹的拦截能力即不满足引理2，则交接班失败。

算例:假设通过目标轨迹预测获得的目标速度为3517.9 m/s；拦截弹在交接班时刻的速度为3332.5 m/s。通过计算可得目标与导弹速度比为p=1.0556，选择PPN比例系数为4。则针对该目标PPN的捕获条件如图2所示。

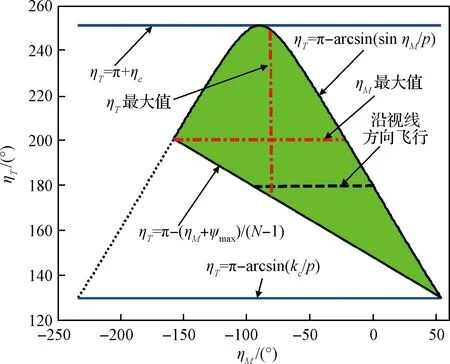
图2 当p=1.0556, N=4时PPN对应的捕获条件Fig.2 The capture region of PPN (p=1.0556, N=4)

2.3 侧窗探测约束条件分析

红外侧窗探测导引头是高超声速目标拦截弹的关键技术之一。在交接班过程中要保证视线被稳定地控制在侧窗视场内。在侧窗探测条件下，纵向平面的制导几何关系如图3所示。

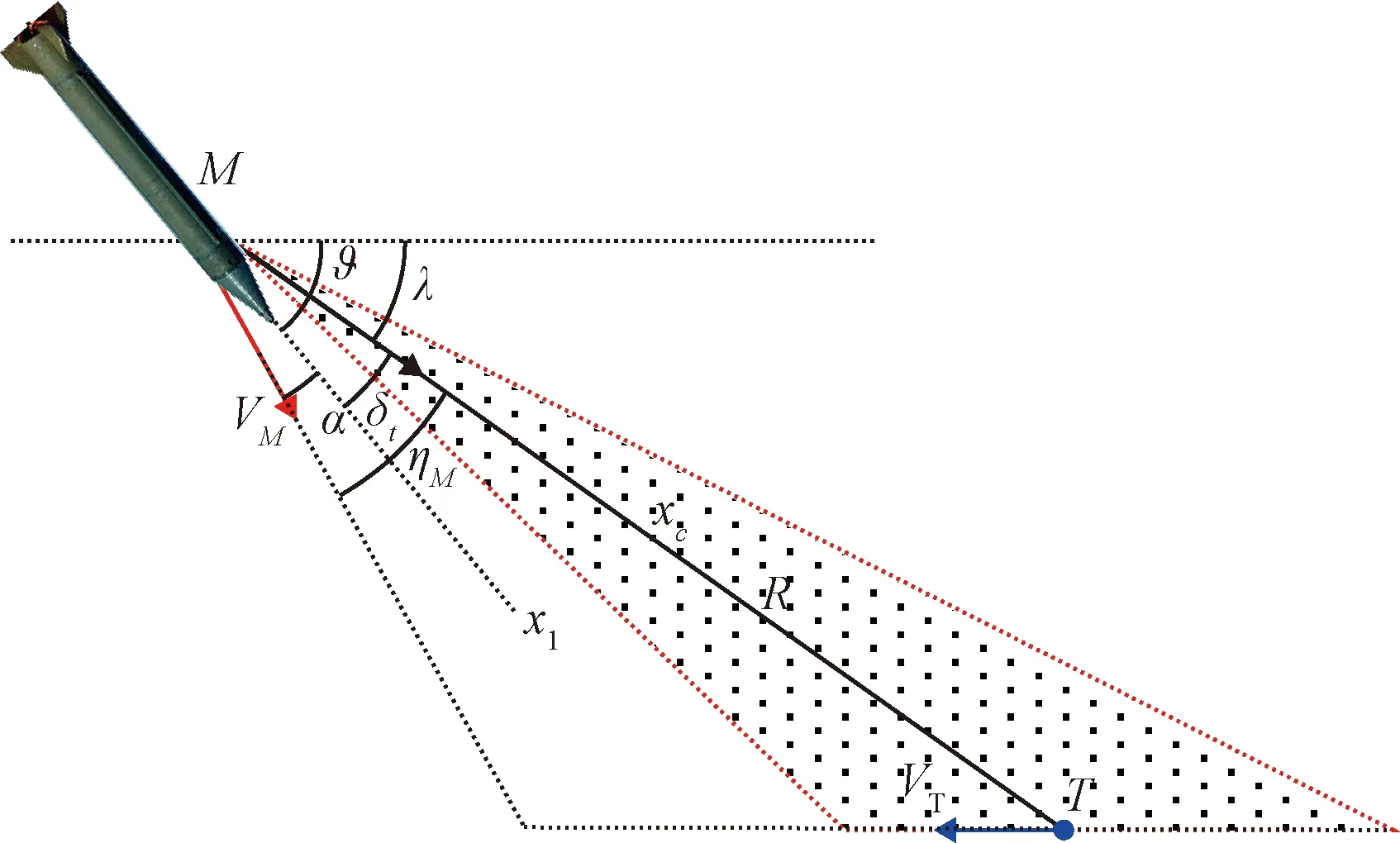
图3 纵向平面制导几何关系Fig.3 Planar engagement geometry in the longitudinal plane

其中，x1表示弹体纵轴，xc表示导引头的光轴方向，ϑ为俯仰角，α为攻角。拦截弹导引头采用全捷联红外凝视导引头，其在弹体坐标系下的跟踪范围为俯仰方向δT=[5°,55°][27]。

α=ηM-δT>0

(21)

ϑ=λ+δT

(22)

在拦截弹纵向平面交接班过程中，导引头侧窗探测问题的实质是如何控制α和ϑ满足上述等式约束。本文将拦截弹视为质点，不考虑其姿态控制问题，将攻角的上述约束条件加到中制导终端约束中。

3 hp自适应网格细化的弹道优化

3.1 Bolza最优控制问题

由于中制导弹道规划问题研究的时间区域为[t0,tf]，而伪谱法所应用的时间域为[-1,1]，所以首先需要通过引入一个新的时间变量τ进行时域变换

(23)

性能指标：

(24)

系统方程：

(25)

过程约束：

Cmin≤C(x(k)(τ),u(k)(τ),t(τ,t0,tf))≤Cmax

(26)

边界约束：

ψmin≤ψ(x(1)(-1),t0,x(K)(-1),tf))≤ψmax

(27)

3.2 基于Legendre-Gauss-Radau配点离散

将整个时间区间划分为多个子区间后，每个子区间内的状态变量用Nk+1次全局多项式进行近似表示为

(28)

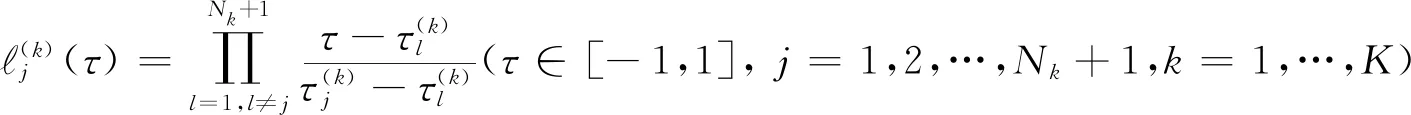
(29)

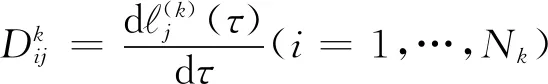
结合前面离散化的结果，最优控制问题在LGR点离散后转化为NLP问题如下：

利用LGR积分将目标函数近似为

(30)

系统方程在LGR点的离散形式为

(31)

过程约束(26)在LGR点的离散形式为

(32)

边界约束(27)在LGR点的离散形式为

(33)

通过上述一系列的数值近似方法，最终将连续的Bolza问题转化为NLP问题，即求得每段LGR点处的状态变量和控制变量，在满足系统方程(31)、过程约束(32)和边界约束(33)的情况下，使得性能目标函数(30)最小。本文将利用内点法(Interior point optimization, IPOPT)求解NLP问题。

3.3 hp自适应网格细化方法

自适应网格细化算法的目的是通过网络重构，提高离散后的计算精度。每个子区间内设定一个离散状态方程和过程约束的误差容忍度ε，如果在当前网格划分条件下，每段子区间内的计算精度大于ε，则对当前的网格进行重构。能够在较低运算代价的情况下获取较高的精度。网格的细化更新需要离散的误差信息，由于最优控制问题的解事先是未知的，因此需要对离散误差进行估计。

3.3.1相对误差的估计

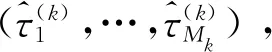
(34)

(35)

(36)

(37)

式中:l=1,…,Mk+1，i=1,…,nx，nx表示状态变量的数量。在网格区间Sk内，最大相对误差可定义为

(38)

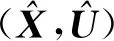
(39)

其中，c是常量，V表示网格配点数，h表示网格区间的宽度，υ的取值与配点个数V有关。式(39)给出了[-1,+1]区域内误差的上界，能够为研究网格细化和配点优化提供了依据。

3.3.2自适应网格更新方法

面向中末制导交接班拦截弹多约束弹道优化往往是一种非光滑的轨迹优化问题，文中引入自适应网格更新方法解决此问题。下面采用状态和控制变量的二阶导数来判断网格内轨迹的光滑程度。

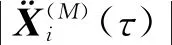
(40)

假设式(40)成立，且在第M+1次迭代中最大相对误差等于容许误差，由式(40)可得

(41)

其中，区间细分个数D可以表示为

(42)

区间细分个数不宜过大，其取值范围为

D≤Hmax=[logNk(e(k)/ε)]

(43)

其中，[·]表示向上取整，Hmax表示子网格区间数量的上界，当e(k)ε时，Hmax大约取15～25，当e(k)→ε时，Hmax趋近于0。

4 仿真校验

本文以拦截临近空间高超声速目标中末制导交接班为研究背景，为了验证本文所设计的hp自适应网格细化方法的有效性以及验证中末制导交接班窗口的合理性。设定了3组仿真场景，仿真1和2主要是验证hp自适应网格细化算法的求解效率和求解精度以及判断拦截弹终端约束可变化范围。其中，仿真1中拦截弹中制导端点状态及约束条件的设置见表1。论文中所有仿真都是在MATLAB®2014a软件上运行，计算机的配置为：联想CPU 3.4 GHz Intel Core i7。NLP问题由IPOPT软件包来求解。取初始网格为10段，最大和最小配点数分别为4和26，容许误差为ε=10-6。

仿真1：为验证文中所设计算法的优越性，将其与传统的高斯伪谱法进行对比。仿真发现hp自适应网格细化的弹道优化过程共进行了4次网格重构，最终求解优化结果所需配点为21个，求解时间为1.257 s，最大相对误差为8.0912×10-7。而高斯伪谱法的求解时间为21.5 s，hp网格优化方法求解效率明显优于高斯伪谱法。究其深层原因，hp自适应网格细化方法在迭代的过程中能够较好的探测到轨迹的非光滑区域，并对节点进行加密处理，这一措施可以有效地提高求解精度，也大大提高传统伪谱法解决NLP问题的能力。

表1 拦截弹再入飞行的端点状态及约束条件Table 1 Initial and terminal constraints of the optimal trajectory

仿真2：为了适应预测命中点地变化，拦截弹需适应在不同终端弹道倾角约束下，满足多约束条件进行正常飞行。下面将验证在单纯在气动力控制下拦截弹弹道优化结果。设定θMf分别取值为-8°,-5°,-2°,1°,4°,7°,10°，则仿真结果如图4～6所示。

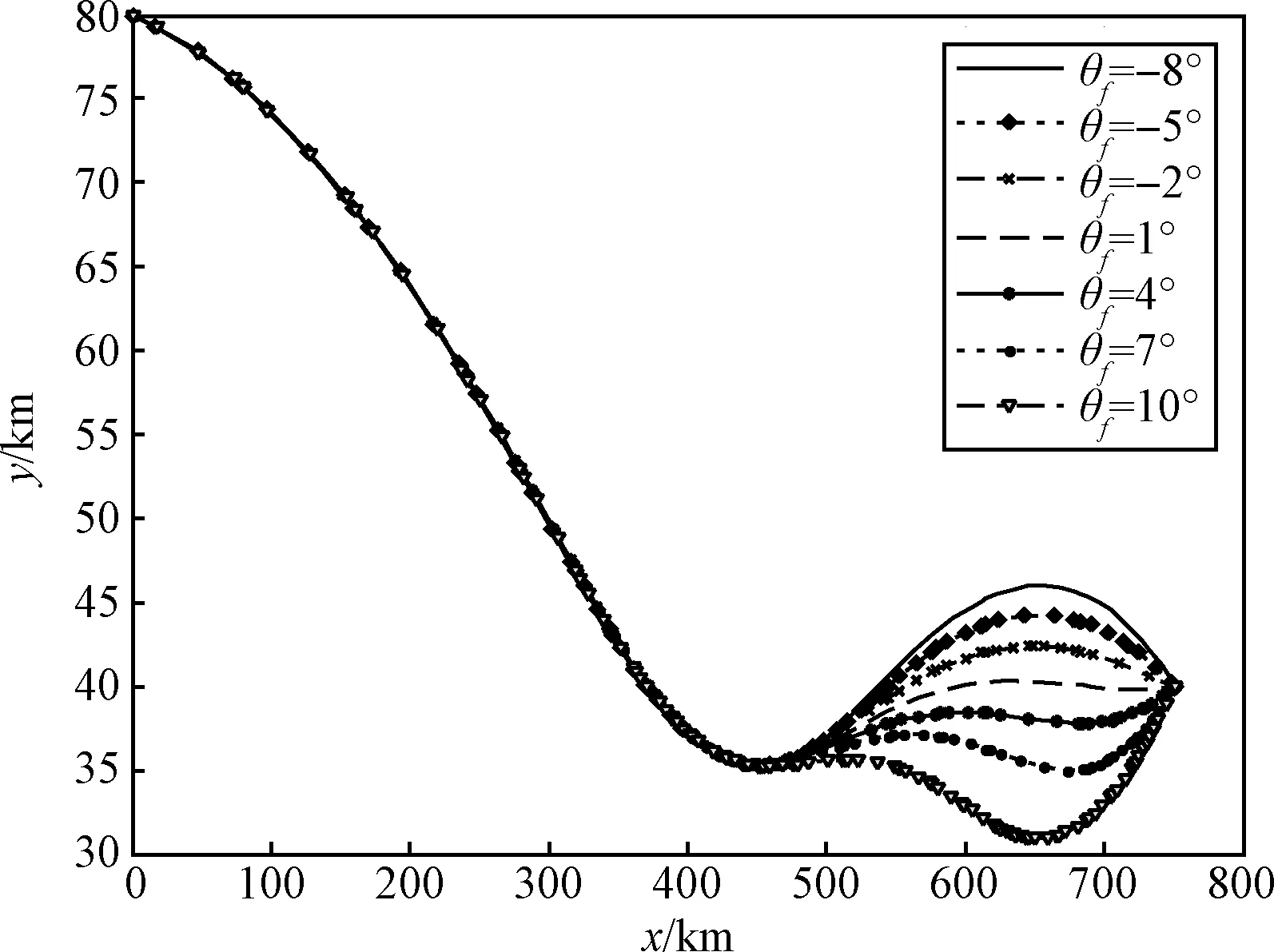
图4 终端弹道倾角变化下拦截弹弹道曲线Fig.4 Curves of the interceptor trajectories with different terminal flight path angles

图5 拦截弹弹道倾角变化曲线Fig.5 Curves of the interceptor flight path angles

从图4可以看出，通过hp自适应网格细化方法优化所得的拦截弹中制导段弹道能够很好地满足不同的终端弹道倾角约束，弹道能够收敛到了预定的终端落点位置，同时能够很好的满足动压、热流和过载等过程约束条件。由图5和图6可知，要使攻角为正值，终端弹道倾角不宜过大。另外，在临近空间稀薄大气下，拦截弹的气动力非常有限，从而终端弹道倾角可变化范围严重依赖拦截弹飞行高度。

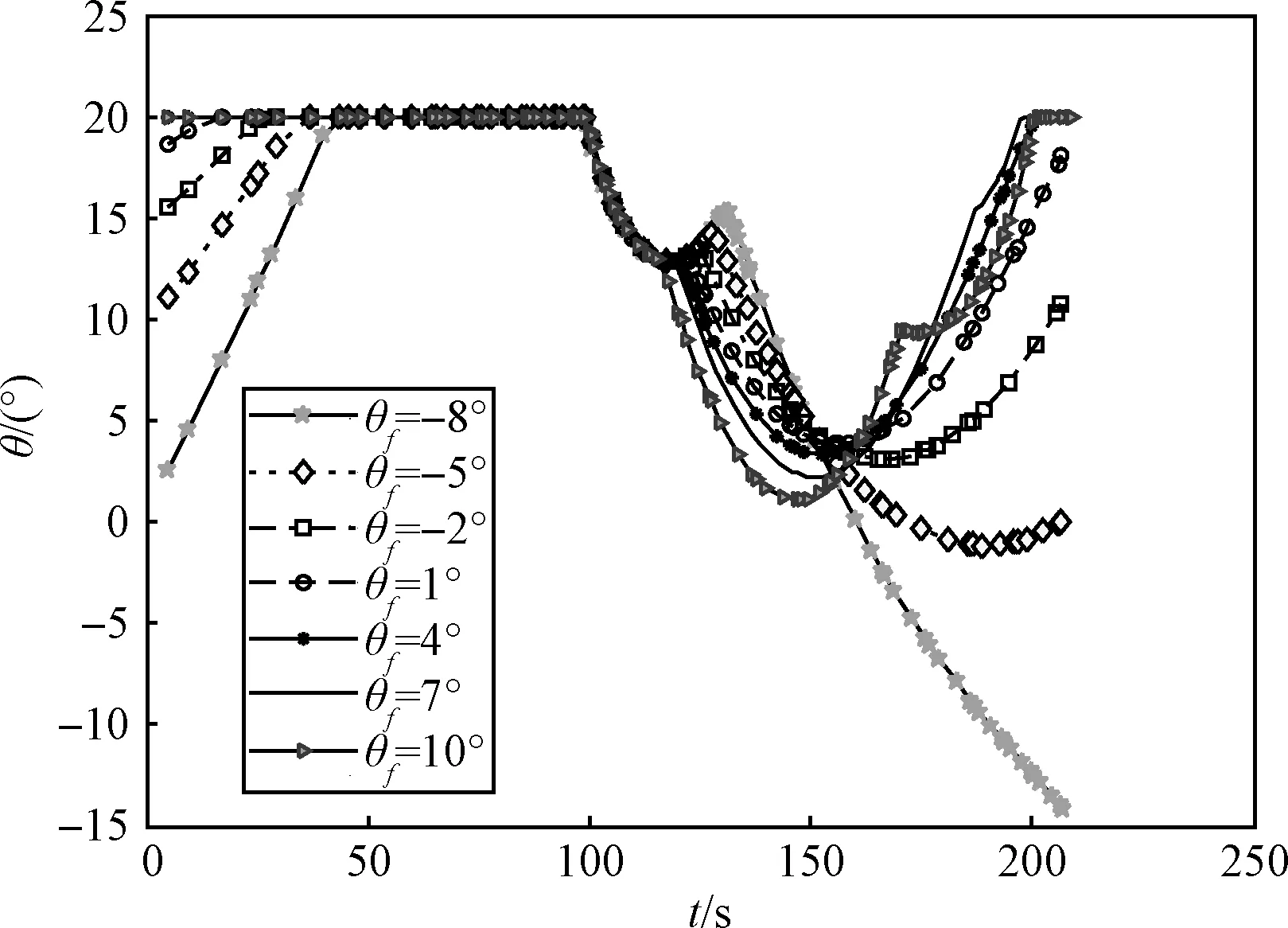
图6 终端弹道倾角变化下控制量曲线Fig.6 Curves of the interceptor control commands with different terminal flight path angles

仿真3：为了证明考虑中末制导交接班窗口约束的弹道优化设计方案的合理性，分别对比导引头迎风和背风两种典型的中末制导交接班情景下导引头的有效覆盖范围。由于高超声速目标滑翔段的飞行高度在20～60km之间。侧窗探测的红外凝视成像导引头的最大探测距离为100km，通过对目标进行跟踪和轨迹预测能够获得目标轨迹信息，目标轨迹滑翔段的轨迹信息如表2所示。

表2 目标预测轨迹的端点状态Table 2 The endpoint state of target prediction trajectory

拦截弹的终端弹道倾角可变范围将直接影响影响导引头对目标的搜索，为了使拦截弹终端弹道倾角具有较大的变化范围，结合目标探测信息，将拦截弹的交接班高度设定为30 km，然而此时导引头热流会影响其对目标的探测。为了验证背风探测的合理性，下面将对迎风和背风探测导引头的有效覆盖范围进行对比。

设定拦截弹中制导终端状态为xMf=750 km，yMf=30 km，θMf=-12°。通过弹道优化得到αf=-2.61°，此时导引头视线角范围为-9.61°～40.39°，其结果如图7所示。

设定拦截弹中制导终端状态为xMf=750 km，yMf=30 km，θMf=-10°。通过弹道优化得到αf=1.44°，此时导引头视线角范围为-3.56°～46.44°，其结果如图8所示。

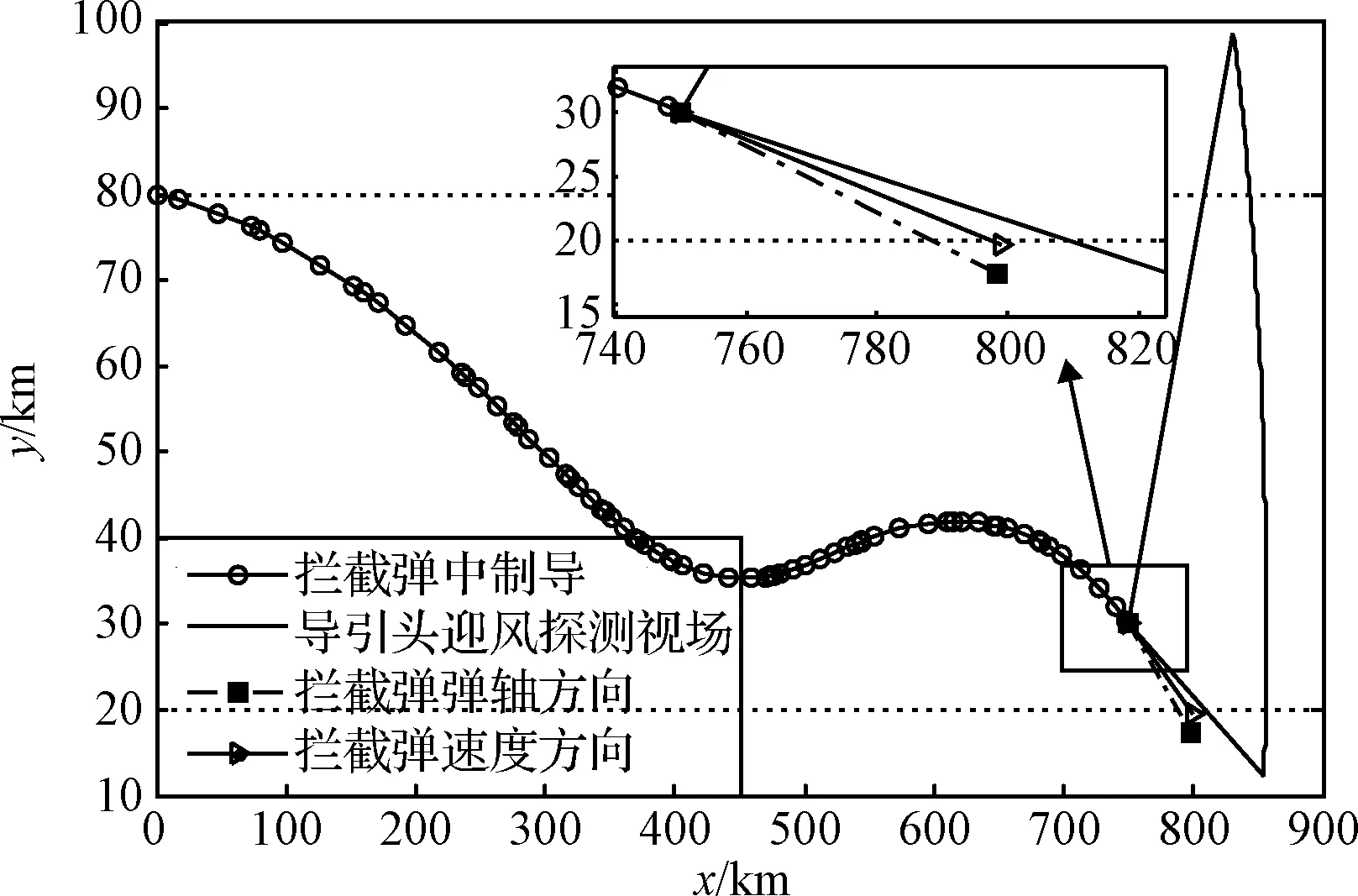
图7 迎风探测时导引头的视场覆盖范围Fig.7 The covering range of seeker field of view under wind detection

图8 背风探测时导引头的视场覆盖范围Fig.8 The covering range of seeker field of view out of wind detection

由图7～8可以看出，迎风探测时导引头视场对临近空间高超声速目标覆盖范围更广，但导引头背风探测可以减轻气动加热对导引头探测目标的影响，同时背风探测的视场覆盖范围也基本可以满足交接班时的需求。

在拦截弹对目标背风探测的背景下，考虑到高超声速目标预测所得轨迹在较大的误差，下面将分析目标轨迹预测误差对拦截弹中末制导交接班的影响以验证中末制导交接班窗口的有效性和合理性。为分析目标的位置预测误差对中末制导交接班的影响，假设其他条件保持不变，设定ytf=28，29，…,37 km，则形成了10条终端位置间隔为1km的目标弹道簇，可表征不同的目标位置预测误差(ytf=30 km为目标基准弹道)。则目标位置预测误差对交接班的影响如图9所示。

图9 目标的位置预测误差对中末制导交接班的影响Fig.9 The effect of predicted position errors on interceptor midcourse and terminal guidance handover

为分析目标的速度预测误差对中末制导交接班的影响，假设其他条件保持不变，设定θtf=-177°,-176°,…,-168°，则形成了10条终端弹道倾角间隔为1°的目标弹道簇，可表征不同的目标速度预测误差(θtf=-170°为目标基准弹道)。则目标速度指向预测误差对交接班的影响如图10所示。

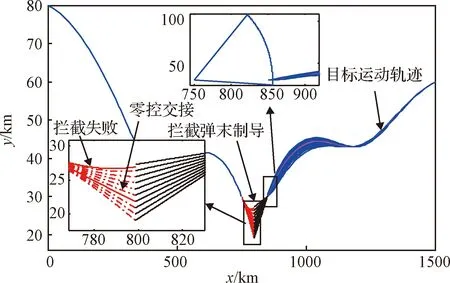
图10 目标的速度预测误差对交接班的影响Fig.10 The effect of predicted velocity errors on interceptor midcourse and terminal guidance handover

从图9和图10中可以看出，拦截弹导引头能够有效覆盖目标的预测轨迹。在交接班时刻当弹目运动状态满足引理3的约束时，拦截弹则可以实现零控中末制导交接班，如图9中加粗线条所示。当目标轨迹的位置预测误差过大而超过拦截弹的修正能力，即无法满足引理2的约束时，则会导致拦截弹交接班失败，如图9中加粗点线所示。而当目标轨迹的速度指向误差过大也超过拦截弹的修正能力时，也会导致拦截弹交接班失败。