复杂约束下航天器姿态机动球面几何规划方法
2021-03-31耿子阳朱圣英李朝玉梁子璇
徐 瑞,耿子阳,朱圣英,李朝玉,梁子璇
(1. 北京理工大学宇航学院,北京 100081;2. 深空自主导航与控制工信部重点实验室,北京 100081)
0 引 言
当航天器在轨运行时,经常需要执行大角度姿态机动,而在姿态机动过程中,航天器面临各种复杂的约束。这些约束可以分为两类:第一类约束来自外部的指向约束,即航天器携带的敏感仪器应禁止指向太阳、月亮等明亮天体。典型的例子是红外天文卫星IRAS,其机载红外望远镜需要远离热源。为了防止直射的阳光影响观察,在姿态机动过程中,红外望远镜指向与太阳方向之间的角度必须不小于特定值。第二类约束来自航天器内部,由于航天器提供的控制力矩幅度以及角速度传感器的量程范围有限,控制力矩和角速度大小等受到约束[1]。针对第二类约束可以通过设计合理的控制器来处理,而对第一类约束问题的研究则较晚,本文提出的多约束姿态机动路径球面几何规划方法主要用于解决第一类约束问题。
用于解决复杂约束下的航天器姿态机动问题(Spacecraft reorientation in presence of constraints,SRPC)的相关算法已经在国际深空探测任务中进行了多次技术验证,代表性的任务有:卡西尼号土星探测任务、费米伽玛射线空间望远镜(简称FIRST/Planck)任务和太阳异常磁层粒子探测器任务。SPRC问题在二十世纪九十年代得到了广泛的研究,Kim等[2]考虑使用凸优化框架处理约束,通过引入参数化的方式提供了可嵌入航天器自主姿态重定向规划算法的SRPC求解器。McInnes[3]提出了一种人工势能函数法用于引导航天器姿态,通过在不期望指向上叠加较高的势能来避免红外望远镜指向太阳和其他明亮区域。Spindler[4]使用控制理论中的微分几何方法推导出姿态机动控制律,在规定的航天器姿态之间采用rest-rest控制,可以自动避免航天器指向禁止方向。武长青等利用非凸二次型描述姿态指向约束,并引入线性松弛技术,不仅能满足复杂约束还可以降低姿态机动的能量消耗[5-6]。
针对航天器姿态机动过程中面临的不同约束,众多学者提出多种解决SPRC问题的算法框架。本文提出的球面几何规划方法继承并发展了Hablani[7]的几何算法框架,该框架对航天器受到的几何约束进行了系统性描述。一般地,几何规划方法首先考虑无约束姿态机动的最优机动路径,然后通过几何算法寻找中间节点,给出姿态机动的指令序列,保证路径满足指向约束。其它算法框架包括势能函数算法[8-9]、约束监视算法[10]、随机智能算法等。其中概率路标规划器(PRM)[11]、快速搜索随机树(RRT)[12-15]等已在路径规划中得到了大量应用。
本文首先建立航天器姿态和指向约束在三维空间和二维平面之间的相对位置及其转换关系。然后,提出了一种多约束姿态路径球面几何递归修正方法。对于只有一个约束的情况可以直接采用该方法进行处理,并且通过保持一定的角度余量,可以解决航天器实际运行路径与规划路径不一致的问题。对于存在多个指向约束的情况,根据是否对当前规划路径产生影响,将这些约束进一步分为有效约束和无效约束,给出了区分这些约束的检测方法。本文将约束检测方法和几何规划方法相结合,寻找中间节点以规避约束区域,以递归的方式处理多约束问题。该方法可以作为姿态规划器的内嵌算法向控制器提供一系列姿态指令。最后,通过与粒子群优化算法仿真对比,校验了该方法具有节省机动时间、计算效率高的优点。
1 复杂姿态约束几何空间描述与模型建立
描述航天器的姿态有多种方式,本文采用欧拉轴/角和单位四元数两种方式描述航天器姿态,姿态四元数与欧拉轴/角的关系如下:
(1)
式中:q0,qv分别为四元数的标部和矢部。本文采用最小角度机动方式,航天器从初始姿态q(t0)机动到给定姿态q(ti),根据欧拉旋转定理,其姿态机动路径为绕e轴旋转θ角。
考虑具有空间指向约束的敏感器件一般都是固定在航天器主体上,其在空间中的指向记为v。v在本体坐标系B下是一个常幺矢vB,但是在惯性坐标系I中会随着航天器的姿态改变而改变,这里记为vI。航天器的姿态q与vB,vI的关系可以表示如下:
(2)
一般地,造成指向约束的来源(如太阳、轨道碎片形成的区域等)在惯性空间中可以看作是静止不动的,这意味着它们形成的空间约束锥在惯性参考系下属于静态约束。因此需要确定v在惯性系下的值vI。根据式(2),vB在敏感元器件安装完成后就确定了,任意时刻vI(t)的值可以通过该时刻的姿态四元数q(t)推算。
航天器的姿态运动学方程描述航天器姿态(姿态四元数表示下的)与角速度之间的关系:
(3)
式(3)也可进一步表示为:
(4)
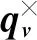
(5)
航天器的姿态动力学方程描述的是执行机构提供的控制力矩与角速度之间的关系:
(6)
将式(6)展开得:
(7)
这里的角速度和控制力矩及其分量都是在本体坐标系下表示的量。
为了便于分析障碍区域与敏感轴的指向关系,需要建立一个在初始指向附近展开的局部坐标系L。局部坐标系L起到了从三维惯性坐标系到α-β平面坐标之间转换作用,在L系附近能较方便的定义方位角α和高度角β,同时也能计算出L系的三个坐标轴轴向矢量在惯性空间中的指向,进而确定空间惯性坐标系与α-β平面坐标之间关系。如图1所示:

图1 敏感轴v与障碍区域s在L系下的关系Fig.1 The relationship between the v and s under the coordinate frame L

(8)
在不考虑约束影响的情况下,实现星载敏感轴从v0机动到vf的路径为绕固定轴Lz旋转θ角,这条路径没有多余的角度机动,因此被称为最小角度机动(Minimum-angle Slew Path)。根据式(1)可以计算出航天器最终时刻相对于初始时刻的机动姿态。障碍区域s在局部坐标系L下有两种表达方式:
(9)
根据式(9)可以推出高度角与方位角的计算方式:
(10)
式中:α的具体取值由坐标(sTLx,sTLy)所在象限决定。障碍区域与敏感轴指向可以用单位球面上的点表示,这些点进而被映射到α-β平面上,如图2所示。

图2 障碍规避问题在α-β平面下的几何表示Fig.2 Geometrical representation of obstacle avoidance problem under the plane α-β
图2中阴影部分表示障碍区域,c1,c2,c3分别是三个障碍区,这样在三维空间中形成的空间禁入锥可以用二维曲面上的圆盘面表示:圆的半径即为禁入锥的半顶角,圆心的位置指向障碍区域的中心天体。注意,这里将α-β平面称为曲面是为了强调该平面的距离测度不同于一般欧氏空间(R2)的测度,因为二者有不同的黎曼度量。
根据纳皮尔圆周定理可以得到α-β平面上任意两点A(α1,β1),B(α2,β2)间的距离公式:
d(A,B)=arccos(cos(β2-β1)·cos(α2-α1))
(11)
2 多约束姿态路径球面几何递归修正方法
根据约束区域对当前路径是否有影响,将约束分为有效约束和无效约束,对于图2所示的路径B1,c1为有效约束,c2,c3为无效约束。注意,c2,c3虽然对路径B1无影响但对后续的规划路径存在影响(如c2对路径B3的影响)。之所以进行这样的划分是因为需要保证:规划最终路径的有效约束个数为零,即满足所有的约束条件。
另一个需要考虑的问题是航天器姿态机动的实际运动路径与规划路径不完全一致,本文把规划的路径划分为B2段与B3段(均为实线段),实际运动的路径用虚线段B4表示。对于B3段,虽然B3满足约束c2但实际运动路径却违反了约束,针对这种情况,本文提出一种增加裕角(γ-φ)的方法将障碍区扩充到禁入区。这样,如B2段所示,即使实际运动路径偏差了规划路径也能避免敏感器视轴进入障碍区域。裕角值的确定与控制器的选择有关,因为不同的控制器产生的实际运动轨迹是不同的。但由于姿态控制系统本质是非线性系统,无法得到路径的解析式,更无法建立控制律与裕角值之间的精确对应关系,所以裕角值的选择需要通过实际经验来决定。
本文进一步给出判断有效约束和无效约束的计算方法,由于在α-β平面中心点到某段路径的距离(测地线的长度)计算困难,需要将点的坐标转换回惯性坐标系表示,可以看成是式(10)的逆过程:
(12)
其中:Li(j)(i=x,y,z;j=1,2,3)表示Li轴在惯性空间中的第j个分量。
记任意一段路径由p1出发到p2,则点s到测地线p1p2的距离为:
d=
(13)
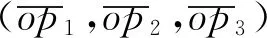

(14)
针对当前路径存在约束违反的情况,尤其是有多个有效约束存在的情况(如图3所示),路径节点的指令序列记为M(vo,m1,m2,…,vf),节点之间的路径为沿着最小角度路线,并与禁入区域相切方式进行姿态机动。
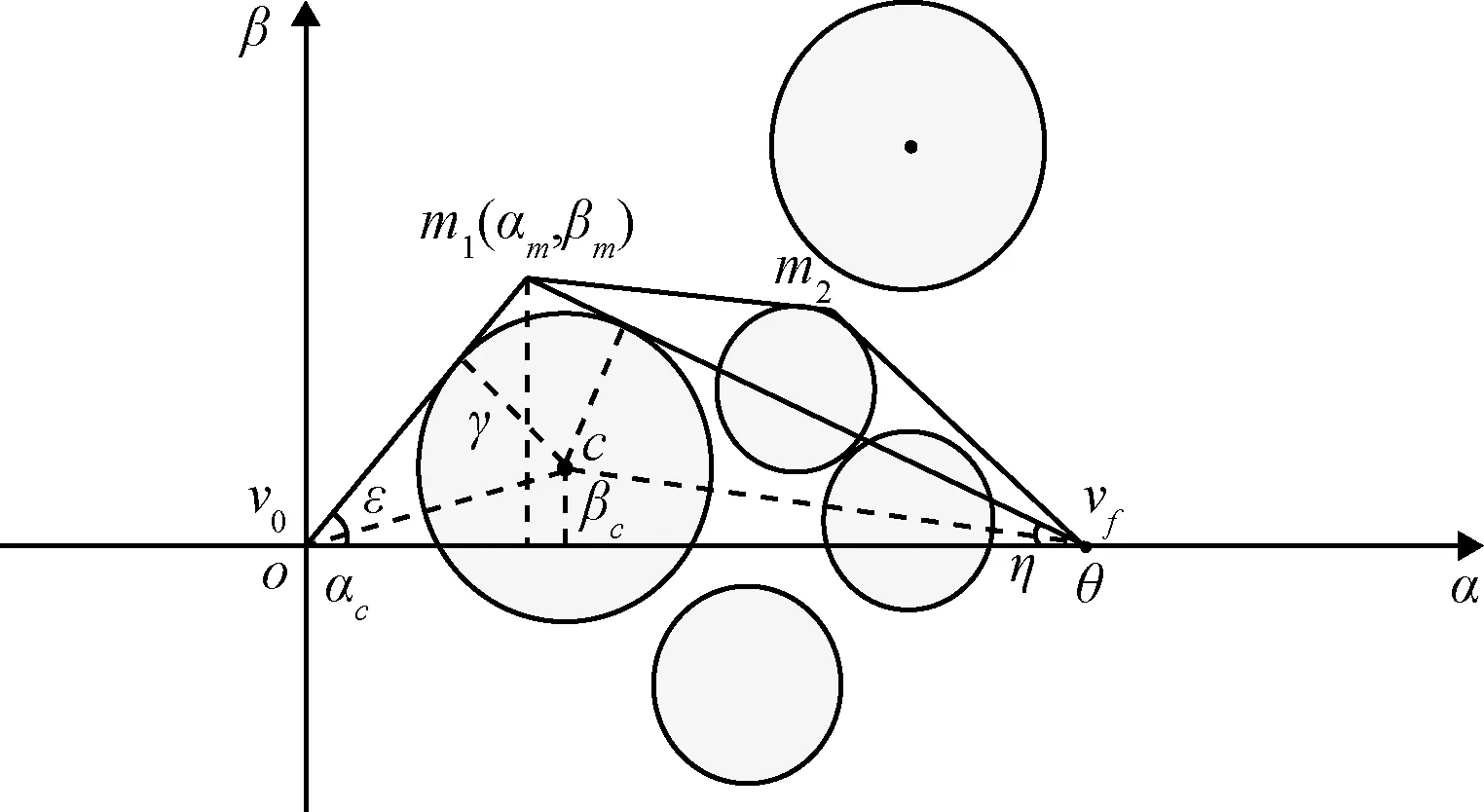
图3 路径节点生成示意图Fig.3 Schematic diagram of path nodes generation
(15)
(16)
式中:ε,η的几何意义如图3所示,αm,βm分别为m的方位角、高度角。路径节点生成的迭代过程如下:

(17)
3 仿真案例与分析
本文仿真案例如下,为了方便计算假定航天器的初始姿态qini=[1, 0, 0, 0]T,姿态机动实现敏感轴从v0=[0, 0, 1]T机动到vf=[0, 1, 0]T即最终姿态qend=[0.7071, -0.7071, 0, 0]T。
航天器的转动惯量J=diag(123,205,147.6)(kg·m2),姿态机动路径的约束模型相关数据计算整理成见表1。
采用本文提出的姿态路径几何递归修正方法计算出姿态规划指令集M见表2。
本文采用粒子群算法作为对比,因为粒子群优化算法本身具有许多优点,第一,实际应用广泛;第二,有许多有效方法避免算法陷入局部最优;第三,部分参数有较为成熟的理论研究方法用于选择。本文采用标准粒子群优化算法流程求得姿态规划指令。其相关参数设置如下:

表1 约束模型相关数据Table 1 Relevant data of the constraint model
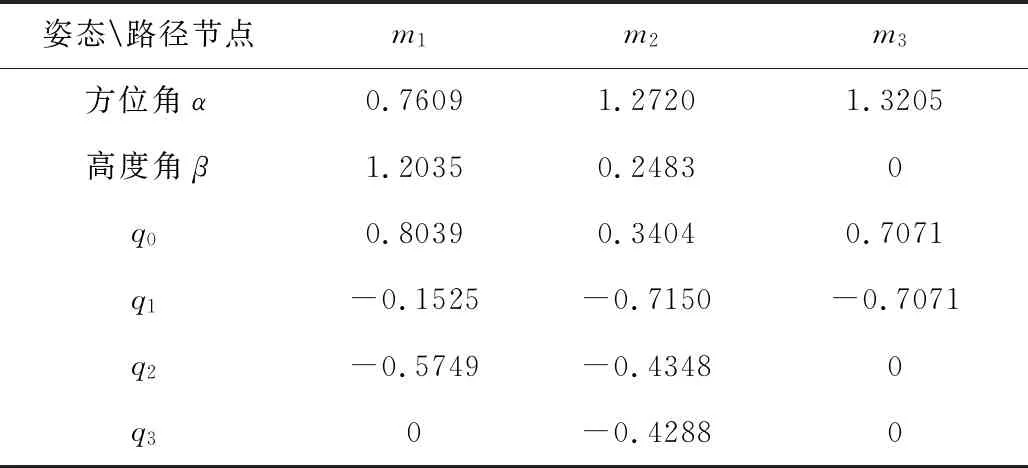
表2 姿态规划指令集M计算结果Table 2 Calculation result of attitude planning instructions set M
初始种群G=100惯性权重η=0.8,自我学习因子与群体学习因子均设为0.5,位置和速度分别限制在±1、±0.05;通过粒子群算法搜索得到的姿态指令集N见表3。

表3 粒子群算法搜索的姿态指令集NTable 3 Attitude planning instructions set N searched by particle swarm algorithm
有效约束个数为零时是球面几何递归修正过程的结束条件,因此姿态指令集M能够自动满足路径约束。而粒子群算法得到的姿态指令集N是通过将路径约束作为适应度函数的优化对象之一来满足约束的。
将规划得到的姿态指令作为控制系统输入,通过航天器姿态机动,使敏感轴安全地完成从初始指向到目标指向的机动。因此,可以将整个姿态机动过程划分为三段,本文对每一段机动过程都进行了仿真。
本文采用经典PID姿态跟踪控制器[16],分别对姿态指令集M,N中给出的姿态位置进行路径跟踪仿真,为了保证整个姿态机动路径光滑性,从一个节点机动到另一个节点采用rest-rest机动方式。整个机动过程可划分为三段,每段仿真结果如图4所示。

图4 球面几何规划算法下的姿态位置历时曲线Fig.4 Attitude position histories using spherical geometric planning method

图5 球面几何规划算法下的姿态位置历时曲线Fig.5 Angular velocity histories using spherical geometric planning method
图4~5表示采用球面几何递归修正方法的航天器在不同阶段姿态与角速度的历时曲线,图6~7则表示粒子群优化算法下航天器的姿态位置和角速度历时曲线。从仿真结果可以看出,按照球面几何规划方法提供的姿态控制指令集,航天器姿态机动最短机动时间为230 s左右,从姿态位置变化来看以最小角度机动的方式完成大约163°的角度机动。从角速度变化来看,整个机动过程实现了rest-rest机动方式,这保证了航天器能实现连续的姿态机动,同时也为非连续的姿态机动提供可能性,即航天器在到达某个路径节点后可停留一段时间,虽然会导致姿态机动时间增加,但是航天器可以利用这段时间再进行调整,为其它系统分配时间资源以保证整个系统的鲁棒性。航天器按照粒子群算法提供的控制指令集在250 s左右完成姿态机动,耗时要多于球面几何规划方法。这是因为球面几何规划方法设计的的路径会掠过禁入锥表面(在考虑裕角的情况下)接近最短路径,所以能节省姿态机动时间。而且,球面几何规划方法是确定性算法,没有随机因素,计算效率要更高。
4 结束语
本文对航天器姿态机动中各类约束进行了分类,提出了一种球面几何规划方法来解决姿态机动的路径规划问题。利用球面几何方法对航天器姿态、敏感轴指向和空间指向约束之间关系进行了推导。然后,进一步将约束划分为有效约束和无效约束,提出了区分此类约束的路径约束检测方法,有效减少了约束处理的数量。最后给出了路径中间节点的解析公式。结果表明,与群智能算法相比,球面几何规划方法具有节省机动时间、计算效率高等优点,对于节省星载计算资源具有重要参考意义。

图6 粒子群优化算法下的姿态位置历时曲线Fig.6 Attitude position histories using particle swarm optimization algorithm
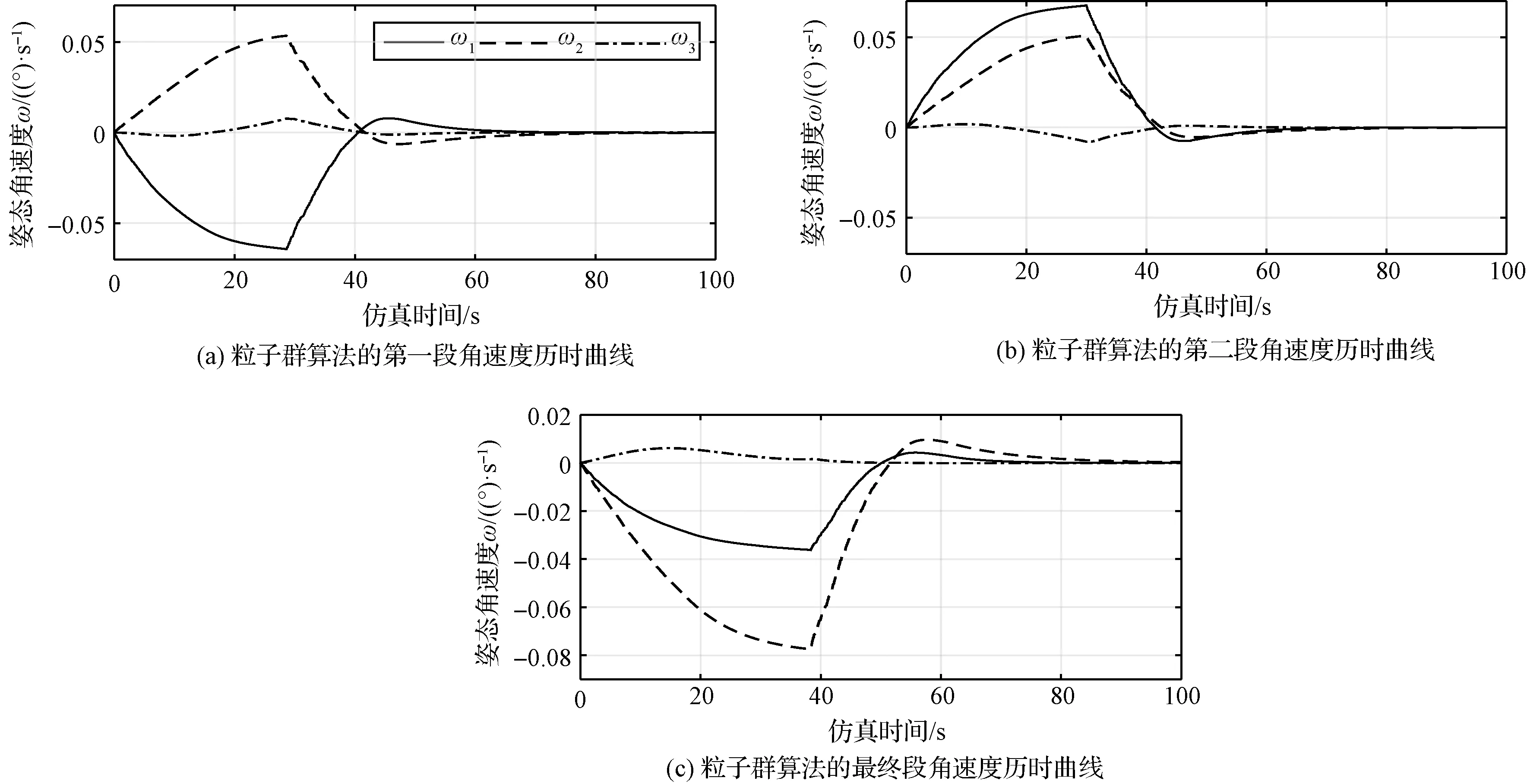
图7 粒子群优化算法下的角速度历时曲线Fig.7 Angular velocity histories using particle swarm optimization algorithm
