《确定位置》单元整体教学设计与说明

文｜梅方玲 裴云姣

一、单元教材分析

“方向与位置”的内容在小学分为四个阶段：第一阶段，认识上下、前后、左右，会用这些词描述物体的相对位置；第二阶段，认识东、西、南、北、东北、西北、东南、西南八个方向；第三阶段也就是本单元，学习用方向和距离描述路线图，能用数对确定位置；第四阶段能根据参照点确定位置。在初中还将继续学习有关平面直角坐标系和函数的内容。可见，本单元的教学中引导学生感受到确定位置的“本质”尤为重要。

二、学情分析

除了对教材进行深度分析，还需要充分了解学生的认知发展水平和已有的知识经验，并对学生的情况进行客观分析。

通过分析，我们有了以下两点思考：

1.教学时要突出用数对确定位置的本质，即数与点的一一对应性，让学生加深对用数对确定位置的理解，引导学生去感受确定位置的三个关键要素：方向、起点和顺序。

2.教学时要突出用数对确定位置的意义，即确定位置方法的结构性。

三、单元课时划分

通过以上思考，我们对本单元的教学做出了如下调整：第一课时的内容不变。在第二课时中，由原来的“在方格纸上用数对确定位置”变成了“探究用数、数对和数组确定位置的本质”教学。也就是从原来的二维，变成了现在的一维（铺垫）到二维（新课）到三维（拓展），帮助学生理解确定位置的一一对应性和结构表示的统一性。

四、教学设计

环节一 情境引入

1.公交站牌。

我是李小明。我家住在月亮湾公园，想一想，你能用数据来表示我要下车的斗谭站吗？

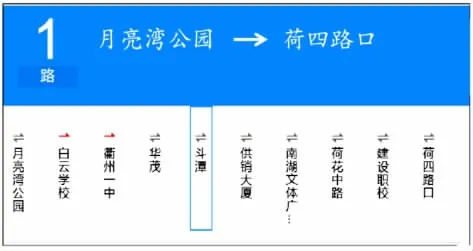
从方向和顺序入手，用一维表示，线→一个数。

2.公交车里的位置。

现在你还能用一个数来表示我坐的位置吗？

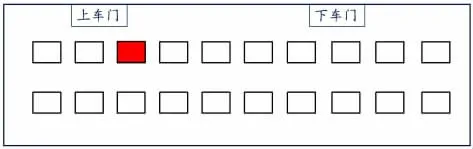
（引出二维表示问题）

环节二 新课探究

这是小明在教室的位置，从讲台的角度看去，你能表示小明的位置吗？

1.规范数对读写。

师：和公交车里的位置比较，现在的行数更多了，那该怎么表示呢？请同学们写在草稿纸上。

（展示学生作品）

（板书：第4 组第3 排 第5 列第3 行）

师：这两位同学虽然表示的位置是一样的，但是表示的方法却不一样，那为什么会有这种不同呢？

生：因为方向不同，一个从左到右，一个从右到左。

师：看来接下来我们得做个规定。在数学中，我们把“竖着数”的叫做“列”，这里一共有几列？（8 列）从哪边开始数？从左往右数，分别是第一列、第二列……；把“横着数”的叫做“行”，它的方向是从下往上数，分别是第一行、第二行……；而且，我们往往先说列，再说行。那么小明的位置，就可以表示成什么？

生：第4 列第3 行。

师：我还看到有同学是这么表示的［展示学生作品43 或者4.3。预设：（4，3）如果有，最后展示，让学生说想法］。你能看懂吗？

（从组排——列行——数对一步步引导学生进入规范表达）

2.从具体到抽象。

师：那这三个点分别用哪些数对来表示呢？

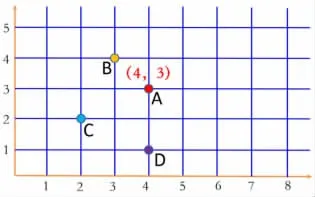
生：（3,4）（2,2）（4,1）。

师：［（指着（4,3）（3,4））］我们来看这两个数对，它们表示的位置一样吗？

生：不一样，第一个数对表示第4 列第3 行；第二个数对表示第3 列第4 行。

师：［（指着（2，2））］那数对（2，2）中，两个“2”表示的意思一样吗？

生：不一样，第一个“2”表示的是列数；第二个“2”表示的是行数。

师：看来每个交点都可以用一个数对来表示。在这些交点里面还有一个非常特殊的交点，在这儿，它能用哪个数对来表示呢？

生：数对（0,0）。

师：这就是我们在用数对确定位置时的起点。

师：梅老师这里还有很多的数对［出示：（3,1）（3,2）（3,3）（3,4）（3,5）］，请你观察这些数对，它有什么特点？

师：如果我想用一个数对来表示这些同学的位置，你有什么办法吗？

生：（3，△）。

师：△可以表示哪些数？

师：（1,4）（2,4）（3,4）（4,4）（5,4）（6,4）（7,4）（8,4）这些数对有什么特点？怎么表示？

生：用数对（△，4）表示。

（通过关键点位置数对分析，进一步巩固学生对于现实位置与图表位置互相转换及数对表达的能力）

环节三 练习巩固（略）

环节四 课堂总结（略）

环节五 新知拓展

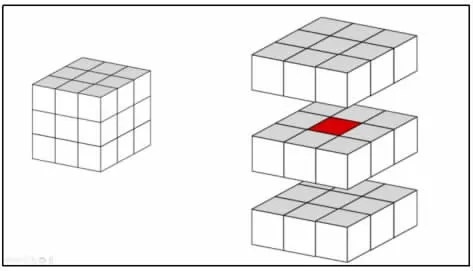
请同学们猜想一下，在“体”上确定一个物体的位置需要几个数呢？