多元引导，开启运算教学的思维之门——《20以内进位加法》教学思考与实践

文｜金宇佶 徐晓良

【教学内容】

浙教版一年级上册第96、97 页。

【背景分析】

20 以内进位加法是基于学生已经学习了20 以内数的读法、写法、不进位加法和相应减法的基础上进行教学的。20 以内进位加法是学生真正学习计算的起点，是学生学习20 以内退位减法及多位数计算的基础，因此本单元的知识在小学数学学习阶段占据重要的地位。

从教材内容编排上看，人教版将本单元的计算部分以加数为线索，分成9 加几，8、7、6 加几和5、4、3、2 加几三个部分，使学生在反复认识的过程中掌握知识和技能。浙教版将不同的加数整合在一节课中，以算法为线索进行编排，并安排了一课多练（一节新课多节练习）。这样的编排方式极大地拓宽了学生探索和发现的空间，也有助于让学生在多种方法的运用、观察、对比中，充分理解算理，并逐渐感悟计算技巧。

在学习本课内容前，学生早已积累了口算20 以内进位加法的生活经验。我们编制了36 道20 以内进位加法口算题，在本教育集团实验校区和附小校区各随机抽取了一个班进行了前测，结果如表1。

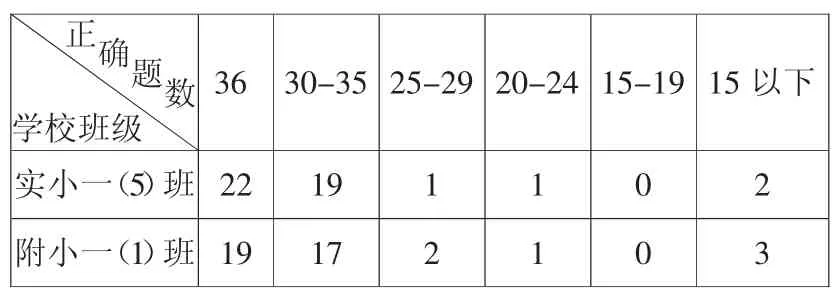
表1：两校区20 以内进位加法口算题正确题数统计表

对前测数据分析发现，大部分学生已经会算20 以内的进位加法，并能得到正确的答案。再对答案正确的学生进行访谈，有将近一半的学生会用“凑十法”来计算，剩余的学生甚至已经进入到盲算阶段。针对学生这样的高起点，本课在梳理所有学生计算方法的基础上，将真正理解20 以内进位加法的算理，体会算法多样化及算法的合理选择确定为教学的重点。教学中，每一个例题解决时都要引导学生思考“怎么算？为什么这么算？还可以怎么算？”用这样三个问题引领学生的思维发展。具体采取了以下两个策略。

1.数形结合，帮助理解算理。

点子图的运用，给刚刚认识20 以内的数、第一次越过“10”的学生以更为直观的“十”的模型。在此基础上，再引导学生借助点子图思考8+5 的计算过程，并在图上通过圈一圈、画一画等方法表示计算过程。在交流每种方法时，让学生用实物移一移，最终将每种方法和与之相配的点子图对应，并呈现在黑板上。式与形的对应使抽象的计算过程得到具体、形象的呈现，不仅有助于学生对计算过程进行数学描述，还让学生清晰地看到算理的形成过程。

2.搭建平台,促进算法多样化。

算法多样化的形成，需要巧妙的任务设计、充分的学习时间与空间保障。在“整理鸡蛋”学习环节，不满足于学生将8 凑成10的方法，通过追问“还可以怎么移？”让学生意识到“凑十法”也有多种可能，为计算多样化埋下伏笔。计算方法的多样，不在于方法的标新立异，而在于让学生根据实际问题解决的需要，灵活选择合理的方法。通过合理选择方法，促进学生思维的发展。

【教学过程】

一、激趣引入，知识铺垫

师：我们把鸡蛋装进盒子里，一盒共能装几个鸡蛋？

（课件出示一盒鸡蛋）

生：10 个。

师：你是怎么看出来的？

生：因为一行是5 个，两行就是10 个。

师：把这些鸡蛋整理一下，看看哪两盒正好可以装满一盒？怎么装？

生：③和④，可以把1 个移到9 个那去。

师：既然可以把1 个移到9个那里，也可以……

生：把9 个移到1 个那里。

生：①和⑥也可以正好装一盒，可以把4 个移到6 个那里，也可以把6 个移到4 那里。

师：剩下两盒能正好装满一盒吗？为什么？

生：不能，因为8 个和5 个合起来超过10 个了。

师：8 和5 合起来，得数已经超过10 了，也就是要进位了。8 加5 到底怎么算呢？这就是今天我们要学习的“20 以内进位加法”。（出示课题）

【设计意图：创设帮农场装鸡蛋的情境，先直观感知一盒有10个鸡蛋，建立单位“十”的直观模型。接着呈现几盒没装满的鸡蛋，通过问题“哪两盒鸡蛋正好可以装满一盒”，激活凑十的经验，为后续“凑十法”计算做铺垫。最终以“剩下的两盒能正好装满一盒吗”，引发进位加法的研究需求。】

二、自主探索，构建算法

师：我们用圆圈代替鸡蛋，看着圆圈图，想想8+5 等于几呢？

生:13。

师：这个13 是怎么得到的？圈一圈、画一画，可以把你的想法表示在圆圈图里吗？

（学生独立探索，并跟同桌交流自己的想法）

方法1：帮8 凑10。

生：把5 个中的2 个移到8个那里。8 个加上2 个是10 个，再加上剩下的3 个就是13 个。

师：我们可以把这个思考过程在算式中表示出来，第一步，把5 分成了几和几？接下去呢？先算8+2=10，再算10+3=13。

方法2：帮5 凑10。

师：还有不一样的想法吗？

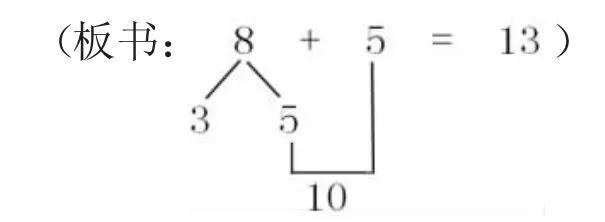
生：因为这边已经有5 个了，所以把8 个中的5 个移过来，5 和5 凑成10，10 再加3 个就是13 了。

师：我们把这种思考方法也用算式表示出来吧！第一步是——把8 拆成3 和5，然后——先算5+5=10，再算3+10=13。

方法3：把8 看成10。

师：老师在其他班上课的时候，有一位同学提出了这样的想法：他分两步做，第一步是——10+5=15（板书），你能猜出他的第二步是怎么做的吗？

生：15-2=13。

师：这两个算式是什么意思呢？你能看明白吗？

生：先假设1 盒装满有10个，10 个加5 个是15 个。可是1盒并没有装满，8 个比10 个还少2 个，要把这2 个减掉。

师：先把8 看大2 就是10，就有了10+5=15。这个结果比原来——大2，所以15 里我们还要减2，15-2=13。

【设计意图：学习的发生在于思维的碰撞。学生自主展示多种算法，自然出现了“拆大数”和“拆小数”两种不同的凑十方法，并在教师提示下理解“多加减补”的方法。展现简单计算背后丰富的推理路径。】

师：同样是计算8+5，我们用了三种方法，结果都是13。这些方法有什么不同？

生：第一种是把5 拆开，第二种是拆8，第三种是把8 看成了10。

师：虽然方法不一样，但在计算过程中它们都有一个共同点，你们发现了吗？

生：都有一个10。

师：你们是怎么想到要和10联系起来的呢？

生：10 加几就等于十几，凑成十以后算起来更加简便了。

师：我们给这种方法取个名字，就叫凑十法。（板书：凑十法）

【设计意图：通过分析、比较、归纳三种方法的异同，引导学生突破算法表面，感悟算理本质，提升数学思维的深刻性和概括性。】

三、练习巩固，拓展提升

师：选择自己喜欢的方法，找到相应的方框填一填、算一算。

师：我们用凑十法解决7+5、8+5、9+5，换成其他的数你还会算吗？你还想用凑十法算几加几呢？

师：金老师这里也有四个算式，你能用凑十法来计算吗？请你在算式上直接写出得数，如果有困难，你也可以在算式下面写一写过程。

4+8= 7+8= 5+6= 8+9=

反馈：直接说出得数，聚焦8+9 的计算过程。

【设计意图：通过“你还想用凑十法计算几加几”的讨论，形成学生相互出题、相互应答、相互判断的交流场景，体现学生的主体性，学生通过出题答题，更加完整地理解计算题的特点，真正内化“凑十法”。通过一组口算练习，鼓励学生逐步压缩计算过程，直接写出得数，进一步掌握算法。】

师：看图，你能提出什么问题？

师：要求一共有多少只，怎样计算好？列算式算一算。

生：5+4+6=15（只）。

生:6+4+5=15（只）。

师：你喜欢哪种计算方法？为什么？

生：凑十法，这样算起来方便。

师：几个数相加时，我们可以把能凑成10 的数先加起来，计算就方便多了。

【设计意图：提供现实场景，培养学生的问题意识和应用意识，并通过“怎么计算好”，引导学生思考、发现：在几个数相加时，可以把能凑成十的数先加起来，进一步推广凑十的方法，为今后学习运算律做铺垫。】

四、课堂总结，知识归纳

（略）

【教学感悟】

运算教学教给学生的不仅仅是技能，更是一种智慧。

在以往的教学中，总会将“拆大数，凑小数”和“拆小数，凑大数”两种方法进行对比，从而优化出“拆小数”的方法，以便于学生更熟练地掌握算法，提高计算速度和正确率。正如新思维教科院姜荣富老师所说：数学知识只是载体，学习知识与训练技能不是教学的全部目的，也不是教学的根本目的。通过计算教学，我们更应达到“以知启智”的目的。在本次教学中，我们尝试让学生用自己喜欢的方法来计算，并不急于对各种方法进行优化，力求让学生在一定量的运算活动中，通过对多种方法的运用、观察、对比、感悟，自然而然地选择合理、简洁的运算方法，形成运算能力。这样的设计给了学生独立思考和自主应用的空间，更多着眼于帮助学生学会学习、持续发展。