复习课的教学实践与策略研究——以总复习《数学思考》一课教学为例

文｜朱 军

翻开人教版六年级下册教科书《复习与整理》（第100 页），粗略一看，这一课是通过解决“6 个点(8 个点)两两相连能连成几条线段”这一问题，让学生化繁为简，采用列表、画图、找规律等策略解决连线问题。如果不去看这一教学内容在教材中的编排，很难想象这是一节总复习课。事实也是如此，许多教师把这节课当新授课处理。

【课前思考】是先整理复习，还是先教学例题

如果先进行整理复习，则需对一至六年级学习中有关数学思考的内容进行梳理。翻阅一至六年级的教科书，有关数学思考的内容不仅多，而且比较散，有蕴含化繁为简思想，有蕴含集合思想，还有蕴含代数思想等等，再加上画图、列表、找规律等这些解决问题的策略，想将这些零散的知识点整理成框架存在很大困难，如果不整理，就失去复习课的意义。

为此，笔者进行了不同路径的多元尝试：或先整理复习数学思考的各种方法、策略等，再把例题作为练习让学生应用；或先教学例题，再复习整理，然后将有关数学思考的方法、策略等整理成框架。经过对比分析发现：“先整理复习再解决例题”的方式，由于缺乏具体实例，学生很难回顾整理，而且在教学过程中依靠学生回忆展开梳理，对大部分学生来说显得空对空，缺乏具象化。而“先教学例题再整理复习”，因为有具体实例支撑，已经有一部分的数学思考方法和策略呈现在黑板上，接着让学生回忆以前所学数学思考的方法和策略，学生基本能够回忆起来，相对来说容易很多。

由此可见，我们可以通过例题教学，先提炼部分数学思考方法和策略，进而帮助学生回忆一至六年级课堂教学中哪些问题也是运用了这样的数学思考方法，这样整理复习，有了一个“半扶半放”的过渡，教学可操作性大大提高。

【课中实践】是挖深点复习一个知识点，还是拓广点复习一整片知识点

作为一节总复习课，它不同于单元复习，最重要的是让学生回顾以往所学数学思想方法，找到联接点，构建知识体系。正所谓“基础知识不求全，而应求联；基本技能不求全，而应求变；数学思想不求多，而在于用”。因此，笔者认为应该从一个知识点入手，进而回顾整理小学阶段相应的数学思考内容，将以前学过的数学方法、策略以及蕴含的数学思想都回忆起来，形成一整片相关知识，让学生梳理并建构数学思考的知识框架。

基于这样的深入思考，笔者设计了以下几个主要教学环节：

【环节1】呈现问题，唤醒数学思考经验

1.课一开始，创设这样的情境：有一天老师仰望星空，突然想到一个数学问题，这么多的星星如果两两连起来，能连几条线段？

2.课件出示百点图，提出问题：这里有100 颗星星，我们把它们看成100 个点，两两相连，最多能连几条线段？

3.进行质疑：到底是多少条，我们可以怎么办？用什么方法解决这个问题？唤醒学生平时解决此类问题的经验。

4.师生探讨后提出建议：点太多，研究起来比较复杂，那我们从几个点开始研究比较好？

5.小结：从最简单的2 个点、3 个点、4 个点……开始研究，再找规律解决100 个点的问题是个好方法，我们就试试这样的方法能不能解决连线问题。

6.呈现表格，学生进行探究。

?

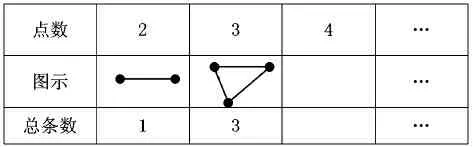
【设计意图：这一教学环节一方面唤起学生曾经解决问题的数学方法和策略；另一方面通过交流、讨论，让学生明白复杂的问题可以从简单入手，探求解决问题的方法和策略。】

【环节2】解决难题，运用数学思考方法

学生自主探究后，通过交流反馈，发现有规律地连有两种情况：一种是每增加一个点，就会增加和前面点数相同的线段数；另一种是从一个点出发能连几条线，再依次从剩下的点出发能连几条线。

其中有规律地连并找出规律是本节课的重点，笔者分8 个步骤进行：

1.出示表格，提问：3 个点能连成几条线段？

2.继续追问，思考：3 条是怎么来的呢？

3.讨论交流，学生边说教师边课件演示。

（1）原来两个点可以连一条线，增加一个点以后就会和前面两个点连两条线，就是3 条。

（2）第1 个点可以连两条线，第2 个点还能连一条线，这样也是3 条。

4.算式表征：教师小结这两种方法虽然想法不一样，但是都进行了有规律地连线，是好办法。那这两种想法能用算式表示出来吗？

（1）1+2=3。（2）2+1=3。

5.寻找规律：4 个点连线的情况又是怎么样的呢？5 个点的情况呢？

6.总结规律：这里的连线存在什么规律？

先让学生四人小组讨论，进而总结：每增加一个点，这个点可以和前面已有的每个点都连一条线段，所以前面有几个点，就会增加几条线段。还可以从一个点出发，能连除它以外的任意一个点，再依次减少直到1 为止。这样两种规律都是可以的。

7.应用规律，解决问题：再回到一开始提出的问题，如果有100 个点，那么可以连几条线段？

呈现两种算法：1+2+……+99 或99+98+……+1。

8.优化算法：教师提出思考，这样的算式我们可以怎么计算？

优化两种算法：（1+99）×99÷2=4950（条）。

【设计意图：这个环节让学生通过列表、画图、用算式表示等策略找到连线问题的规律，进而解决问题，看似解决一道题，其实在解决问题的过程中学生不断运用各种解决问题的数学思考方法和策略，为下一步梳理数学思考做好铺垫。】

【环节3】回顾过程，梳理建构数学思考框架

教师引导学生回顾：在解决这个难题的过程中，我们是怎么思考的呢？

学生交流讨论：我们遇到难题的时候先化难为易，从简单的两个点出发，再通过列表、画图、算式等策略找到规律解决难题。

教师继续追问：在我们小学数学学习过程中，还有没有这样的解决经历？

师生回顾整个小学阶段学过的“打电话”“植树问题”“鸡兔同笼”……都用到了化繁为简、化难为易的数学思考方法。还发现以前也一直在用画图、列表、计算等策略和方法帮助我们数学思考，找到规律，解决问题。

小结并板书：看来数学思考的方法和策略在我们解决问题的时候非常重要。我们可以从简单入手，通过画一画、列表、算式表征等策略找到规律，并应用规律解决复杂的问题。

【设计意图：通过回顾解决问题的过程，唤起学生曾经解决问题的数学思想方法和策略，让学生发现原来我们六年来的数学思考学习其实是有联系的，很多地方用到的方法都是相同的，从而构建数学思考的知识框架。】

【课后启示】总复习课的几点教学策略

小学数学总复习不同于单元复习、学期复习，从学生学的角度看：知识容量多、跨度大、时间长，所学的知识遗忘率高，整合的难度相当大；从教师教的角度看：时间紧、内容多、综合性强，难以在一节课时间里做到面面俱到，取得很明显的复习效果。特别是总复习《数学思考》这块内容，更是例题少、容量大、时间跨度长、内在联系隐秘……如何才能对这块知识进行有效的整理与复习呢？笔者认为可以有以下几种策略。

1.重视整理与应用相结合。

总复习中关于《数学思考》这块安排了四个例题。可以发现，四个例题都是以问题情境（两个现实情境，两个数学情境）的形式出现，引导学生联系实际或联系数学实例，在解决问题的过程中，回顾以前所学过的数学知识与方法、基本数学思想和基本活动经验，进行有效地整理与复习。因此，教学中我们应该注重将知识的整理与应用相结合，在课堂的起始阶段先教学例题，让学生在解决问题的过程中逐渐回忆起曾经学过的数学方法和数学思想，为下一步进行知识梳理提供具体实例支撑，让学生有内容可以梳理，避免一开始就进行整理而出现的“空对空”现象。

2.重视知识间的内在联系。

总复习时我们应该注重沟通知识间的内在联系，把平时相对独立学习的知识以分类、转化等方法串联起来，使要整理的知识条理化、结构化，形成整体框架，以加深学生对所学知识的理解。《数学思考》这块内容的复习涉及的是数学方法和数学思想的整理，要找到知识间的内在联系就显得尤为重要。因此，教学中我们要安排充足的时间让学生进行梳理，有时学生的整理可能不够确切、不够全面，这都是真实的、自然的现象，我们可以引导学生思考类似的问题：

（1）在解决问题的过程中用到了哪些数学方法？

（2）在以前的学习中，我们用到过这些方法吗？

（3）在解决问题的过程中，是怎么用这些方法的？

（4）它们之间有怎样的联系呢？

采用“问题串”的方式，一方面横向寻找各种数学思想方法间的联系；另一方面纵向体会各种数学思想方法的演变，避免产生重例题教学轻知识梳理、重技能训练轻方法整合的现象。

3.重视整理方法的渗透。

总复习应该让学生更好地学会整理，对于数学思考中那些零散的、跨段的、独立的思想和方法，需要掌握一定的整理方法使之形成脉络框架。我们可以采用回顾学习过程的方法，让学生回顾解决问题过程中用到的数学思想方法，帮助学生从解决问题的角度串联数学思想和方法；也可以采用思维导图的方法，抓住数学思想方法的原点和生长点，从数学思想和方法内在之间的联系整理成知识框架；还可以采用连点成面的整理方法，每碰到一个知识点，引导学生回顾与之相关的其余知识点，慢慢扩散并最终形成知识网。

4.重视练习的整合性和针对性。

总复习的练习设计不应该追求大容量、高密度的题海战术，而是要针对数学思想方法出现的不同情况，设计有针对性的练习，或一题多变、或一题多解、或多题同解，特别是要对例题中没出现的数学思想方法进行补充，尽可能覆盖知识点。此外，总复习练习设计还要凸显整合性，根据知识间的内在联系进行整合，“并联”习题，以系统性的眼光设计练习。