在收与放之间助力思维的发展——《有趣的等式游戏》磨课小记

文｜周 霞 陈 敏

数学教学主要是指数学思维活动的教学。在小学数学课堂中，教师需要花时间去研究学情，基于学情精心组织数学学习活动，设计具有开放性、挑战性的教学任务，给学生展示和发展思维的机会。以下分享《有趣的等式游戏》一课的尝试与反思。适用年级为一年级。

片断一：

出示问题：请将3、4、5、6 填在下面的方框中，使等式成立。

□+□=□+□

1.请学生当小老师读一读题。

师：你们明白题目的意思吗？等式怎样才能成立？

生：两边结果相等。

师：请将你的方法写在练习纸上。

2.学生自主尝试，教师巡视指导。

3.指名汇报。

师：谁先来分享自己的方法？

生：我用凑数的办法。3+6=9，4+5=9，所以3+6=4+5。

师：这位同学是怎么想的？

生：他是用算的办法，左边3+6 等于9，右边4+5 也等于9，所以3+6=4+5。

师：那有没有不用“算”的办法来写等式的呢？

生：我是这样想的：3、4、5、6中，3 是最小的，和最大的6 搭配；4 是第二小的，和第二大的5 合在一起，3+6=4+5。

师：大家听明白他是怎么做的了吗？

生：听明白了，就是把大的数和小的数加起来。

小结：像3、4、5、6 这样四个连续的数，我们可以用最大数和最小数，次大数和次小数“手拉手”组等式。

片断二：

师：老师往里面增加一个数，你还能自己完成组等式的任务吗？

出示问题：请把3、4、5、6、7中的四个数字填在下面的方格中，使等式成立。

□+□=□+□

2.指名汇报。

师：现在大家至少都写了一个等式。老师这里收集了几份答案，我们一起来看一看。

（1）3+7=5+6。

师：这个等式怎么样？

生：他写得不对：3+7=10，5+6=11，等式不成立。

（2）3+7=4+6。

生：最小3 和最大的7 加起来，第二小的4 和第二大的6 加起来。

生：我检查过了，3+7=10，4+6=10，3+7=4+6，等式成立。

师：用什么方法组等式的？

生：其实和刚才是一样的。最小配最大，次小配次大。

师：这位同学的线连得真好，一连线我们就看清楚了：用最小配最大，次小配次大。我们用“大手拉小手”来比喻好不好？

师：“大手拉小手”以后，中间的5——

生：没有用到，去掉了……

（在课件中演示学生的方法，形成板书——去中间）

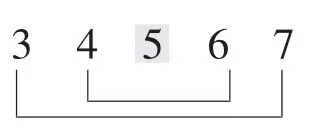
（3）3+6=4+5。

师：请介绍一下你的式子。

生：我想到5 可以去掉，那其他数可不可以去掉呢？最简单就是把7 去掉，变得和刚才的题目一样，3+6=4+5。

师：请你暂停一下。这段话大家听懂了吗？

生：我听懂了。他的意思就是还可以把7 去掉，然后“大手拉小手”，3+6=4+5。

师：（在课件中演示学生的方法）这次去掉了——尾数。

（形成板书——去尾）

（4）4+7=5+6。

生：我可以补充吗？既然可以去掉尾巴的数，那我们还可以去掉头上的数，把3 去掉，“大手拉小手”是4+7=5+6。

（形成板书——去头）

3.反思小结。

师：现在我们得到了3 个答案。回顾一下，我们是怎么做的？

生：我们先想到“大手拉小手”，正好去掉了中间数。后来想到既然中间数可以去掉，还可以去掉头上和尾巴上的数，又得到了2 个答案。一共有3 个答案。

生：我有一个问题，“4”可不可以去掉？

生：不可以，4 去掉以后，3、5、6、7 不连续。我算过了，3+7=10，5+6=11，不可以“大手拉小手”。

生：只有头、尾、中间的数可以去掉。

师：同学们有没有想过这道题和上面的题之间有什么联系？同桌商量商量。

生：去掉尾巴数以后，3、4、5、6、7 变成了3、4、5、6。第二题变成了第一题。

生：从第一题增加1 个数变成第二题，答案增加了。我们发现去头、去尾，都可以剩下4 个连续的数。

生：都可以用“大手拉小手”的方法写出等式。

生：我来补充一下，不可以随便去掉数，有时剩下的4 个数不能“大手拉小手”组成等式。

师：同学们真会学习。我们通过去头、去尾、去中间的方法，把第二题去掉1 个数后，从5 个数的问题变成和第一题一样的4 个数的问题，又可以用上第一题中大手拉小手的方法写等式了。学习数学，我们要不断寻找题目之间的联系，把新问题变成老问题，用老办法解决新问题。

片断三：

出示问题：将3、4、5、6、7 填在下面的方框中，使横行和竖列上3 个数的和都相等。

师：和第二题有联系吗？你能想到好办法来解决这个问题吗？

1.学生自主尝试，教师巡回指导。

2.小组交流。

师：完成的同学把自己的方法说给身边的同学听一听。没完成的也可以说说自己的困难，让小伙伴帮忙一起想想办法。

3.集体交流。

师：说说你们的方法吧。

生：我是这样填的——

师：我们来检查一下填对了没有？

生：7+5+3=15，4+5+6=15，填对了。

师：题目要求横行3 个数的和要等于竖列3 个数的和。所以3个数加一加，可以肯定填对了。（板书：7+5+3=4+5+6）

师：老师这里有一个检查办法，你们看行不行？横的，我只算4+6=10；竖的，我只算7+3=10。我觉得这样就可以保证横行和竖列的和相等了。

生：可以。因为横行、竖列都要加5，都要加也可以都不加。

生：（修改板书：7+3=4+6）这位同学的意思就是等式两边都有“+5”，可以都去掉。所以老师的方法是可以的。

师：反过来说，只要7+3=4+6——

生：两边再都加上5，结果还是相等的。

生：老师，我知道了。这道题看起来是3 个数的和相等，其实是2 个数的和相等。

生：就和第二题一样。把5 放在中间，两边填3+7=4+6。

师：是这样吗？（框起第二题板书“去中间”的条目）那现在你有更好的办法来填这个十字格了吗？请你顺着刚才的讨论再想一想，试一试。

4.学生再次自主尝试，教师巡回。

5.集体再交流。

生：刚刚发现只要两头的数相加和相等就可以，第一个答案，我们是把中间数5 填在中间（指方格），“大手拉小手”。那么接下来我们也可以把尾巴数7 放在中间，然后“大手拉小手”；或者把开头数3放在中间，再“大手拉小手”。

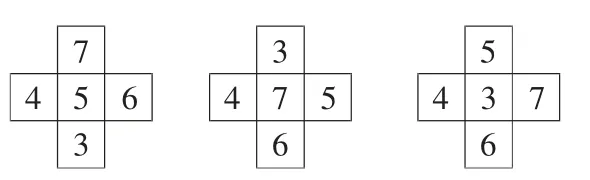
师：谁来当小老师检查？

生：3+6=9，4+5=9。9 都要加7，每行、每列的和都是16。

生：4+7=11，5+6=11，11+3=14，每行、每列的和都是14。

生：这道题和第二题其实是一样的，刚才去掉的头、尾、中间，这里就摆在中间的格子里，剩下的数“大手拉小手”就好了。

片断四：

师：看看，这节课我们解决了这么多有挑战的任务，你有什么想说的吗？

生：这些题目都是差不多的。

生：都可以用“大手拉小手”的办法。

生：如果有多余的数，先要去头、去尾、去中间。

生：填等式也可能变成填格子。

师：填等式还会变吗？

出示问题：把2、4、6、8、10 填入下图的5 个小圆中，使横行和竖列上3 个数的和都相等。

【教学反思】

一、学生的思维是做出来的

《数学课程标准（2011年版）》中指出：有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探究与合作交流是学生学习数学的重要方式。在课堂教学中，教师不仅要为学生设计富有开放性和挑战性的教学任务，而且要懂得和舍得留给学生充足的实操、探索与交流的机会，让学生在动手“做”数学中感知问题本质，探索解题策略，积累解决问题的经验。

学生对一个问题的认识是在做的过程中逐步深化的，解题的方法也是在做的过程中逐步优化的。在用3、4、5、6 组等式时，由于数字少且数值小，很多学生都是直接计算得到答案3+6=4+5 的，采用大数配小数的学生是少数。但在从3、4、5、6、7 中选4 个数组等式时，由于数字有冗余且涉及到了进位加法，学生在实际操作中自然感觉到计算的方法不那么高效，于是转向搭配策略的人数就多了起来。搭配策略的迁移水平是不同的，多数学生比较受限，只想到了大小搭配——3+7=4+6，只有少数继续尝试了“去尾”“去头”法搭配……这种参差的、自发的策略水平恰恰为下一步交流、比较和提升奠定了“愤”“悱”的认知基础和情感氛围。

二、思维发展离不开反思

“学而不思则罔，思而不学则殆。”边学习边反思，不仅可以检查学习过程中的疏漏和错误，还可以理清思路、深化知识、积累经验、优化提高。

在学生做的基础上，组织反思、交流尤其重要。如前面提到学生在5 选4 组等式的活动中，多数学生只能做简单的迁移，得出一个答案，少数学生也只是在懵懂的尝试中找新答案，这时就需要通过交流来归纳、提升。先把多数学生都能想到的答案核对和沉淀下来，引导注意从留下的4 个数转向去掉了哪个数，从而发散思维：还可以去掉哪个数？从一个答案推向多个答案。在此基础上，学生主动质疑：4 可以去掉吗？讨论突出大小搭配策略的适用条件——“连续”的数（实质为和不变的性质：对应加数之间的差相等，即a+b=c+d，有c-a=b-d）。师生、生生之间均在吸取他人思考的基础上继续思考、解释、质疑、拓展，将对问题的认识和策略的优化层层推进，思维从肤浅到深刻、从单一到多元、从碎片到关联。