打磨 打通 打开 高观点视角下的复习与整理
——以《正、反比例复习》为例
2021-03-30钱建兵
文|钱建兵
“高观点”思想是德国杰出的数学家菲利克斯·克莱因于20世纪初在《高观点下的初等数学》这本书中提出来的。克莱因认为,基础数学的教师应该站在更高的(高等数学)视角来审视、理解初等数学问题,只有观点高了,事物才能显得明了而简单;一个称职的教师应当掌握或了解数学的各种概念、方法及其发展与完善的过程以及数学教育演化的经过。数学教材的编排具有螺旋上升的特点,知识之间的层级较为明显,教学中需要在更高的视角审视、理解层级较低的问题,从而理解数学的本质。早期通过铺垫、渗透的知识,在高级阶段通过适当地唤醒、拾取,学习者前后的经验得以延续与贯穿,形成知识的序列与结构。如学习新知过程中的复习铺垫、反思回顾等环节,就是一种唤醒旧经验连接新经验的过程。本文以《正、反比例的复习》为例,着眼于高观点,瞻前顾后,从而达到融会贯通、深度理解知识的教学目标,形成完整的知识结构。
一、打磨已知:在比较中精致结构
格式塔心理学认为:学习主要不是加进新痕迹或减去旧痕迹的问题,而是要使一种完形改变成另一种完形。这种完形的改变可以因新的经验而发生,也可以通过思维而产生,学习就是知觉重组或认知重组,知觉重组或认知重组注重的是认清事物的内在联系、结构和性质。只有通过整理比较,形成清晰的结构,才能更有效地去融合之前的知识与经验,将两个独立存在而实质具有联系的结构进行融合。对概念的清晰认识是建立良好知识结构的前提,所谓清晰,就是要厘清相似概念的联系与区别,从更细致处去把握概念,将原有认识进行打磨,在形成知识结构的基础上整体把握知识的本质与内涵。如对正比例与反比例的理解,不是仅从外部“比值一定”“乘积一定”或是图象上去区别二者,而是要深入概念的整体与内部,增强学生对比例是表示关系即函数思想的理解。“正”“反”是相对的概念,只有通过对比,才能体现自身。
通过两个例子对两个概念进行梳理。经过比较,得出了正、反比例的相同点:都有两个变化的量,一个量的变化引出另一个量的变化,且变化中都有不变的因素。在此基础上,可以打磨细节,让学生说一说对“正”“反”的理解,有的学生从变化方向角度去解释,也有的学生从图形利用图象进行描述。根据学生的回答形成下表,由此学生对正、反比例相同与不同的认识从粗糙走向精致。

?
通过学生条理清楚的表达,以表格、思维导图等形成知识之间的联系。通过具体例子,首先帮学生提取相关概念的内涵与外延;再组织比较,形成了比较清晰的正、反比例的概念结构。要特别重视结构的精致过程,结构越通透,其吸纳整合其他知识、同化融合其他结构的能力就越强。
二、打通旧知:在“吐故”中融合结构
结构融合即建立新结构与原有概念或结构之间的联系,把原有概念与结构纳入新的认知结构中,使原有概念被赋予新的意义与视角。由于之前是以渗透的形式教学,是经过了适合儿童思维水平改造后呈现,所以知识呈现的视角会与正式学习时有所不同。当儿童正式学习某一知识时,因首因效应,对先前改造后学习的知识会有深刻的印象,后期学习时也不会从新的视角去认识,结构的整合并不是自动的。所以教学要在恰当的时候积极寻找中间地带,促进两个结构系统对质,并积极促进旧的结构同化融入到新的知识结构之中。
正比例与反比例在学习了乘、除法的计算之后逐步渗透,教材以探索规律的形式让学生感受变化的思想。如(图1):

图1
这样的例子在教材中非常多,有练习中的也有以规律、性质等教学形式出现的,如商不变的规律、分数的基本性质、比的基本性质等。可以说,通过之前的学习,学生能感受到一个量的变化引起另一个量的变化,对变化的方向也较为清晰,但不能跟正、反比例联系起来,也不能建立起变量的概念,算术的思维始终影响代数思维的发展。对规律的解释,还只是一种经验,缺少相应的理性抽象的思考。因此,从学生思维发展的角度讲,需要一个提升与转变。
从正、反比例的学习过程来看,需要融会贯通才能深度理解。在教学中,我们发现学生是基于具体计算比值相等、乘积相等或图象直观去判断两个量存在哪种比例关系,对于用关系式进行判断,由于不能(或缺少相应的元认知)将自己想到的关系式根据乘、除法之间的关系转化后进行判断,学生对正反比例的判断能力较差。如,三角形的底一定,面积和高是什么比例关系?学生首先想到的是面积计算公式,而不会主动地将这个公式转化成面积除以高等于底除以2,然后判断比例关系,但是却知道“面积不变,底扩大多少,高要缩小多少”这样的关系。
在对正、反比例的概念进行梳理之后,引导学生用比例去思考之前学过的知识,以深化对比例的认识。
首先是乘法中的变化规律。出示(图2):

图2
说一说这是什么规律?能用比例的知识解释吗?并让学生用字母关系式a×b=c(a、b、c 均不为0)表示,说一说三个量的比例关系。在完成抽象表达之后回到情境,说一说常用数量关系中的比例关系:单价×数量=总价、工作效率×工作时间=工作总量……
接着是从比例的视角发现除法中的变化规律。用字母关系式:a÷b=c(a、b、c 均不为0)表示后引导学生用比例的知识解释:商不变的规律、分数的基本性质、比的基本性质。小结:一个乘法或除法关系式的三个量中,只要一个量确定了,就可以确定其他两个量是正比例或反比例关系。可以根据乘法或除法关系式判断比例关系。用比例的眼光看面积、体积的变化规律:正方形边长乘以或除以一个不为0 的数,周长怎么变化?圆的半径扩大3 倍,周长怎么变化?
当学生从现在的学习角度去看原来的知识与结构并获得一种解释时,不仅仅是一种结构的形成,更是理解上的深入。学生会产生“原来那就是比例,原来比例就是之前学习的变化规律”的想法,这样更有助于学生理解比例的意义。通过这样的回顾,从一个更高的视角看原有的知识,“站起来环顾四周”更容易有一种整体感,促进原有知识的同化或顺应,让新结构得以形成,理解得到深入。
三、打开未知:在“纳新”中延伸结构
当旧知通过反思融入结构中,产生一个新结构,结构仍处于平衡状态。这时,教学要引导学生再一次制造冲突,制造新的不平衡,将这个结构开放、生长、延伸。皮亚杰认为,全部数学都可以按照结构的建构来考虑,而且这种建构始终是完全开放的……这种结构或者正在形成“更强的”结构,或者在由“更强的”结构来予以强化。
从复习课的角度讲,复习的要点在于沟通知识之间的联系,形成更大、更清晰、更牢固的知识网络。所谓更大,就是瞻前顾后,站在现在去俯视原有的知识,将原来教材中渗透的、不系统的知识放到现在的一个比较系统的知识中,形成一个结构。瞻前,就是如本课中,对乘、除法运算中的变化规律从正、反比例的角度对其解释。顾后,就是将现有知识放在一个更高的观点上,让学生更近距离地去接触这一知识的本质,正、反比例是函数的学习基础,让学生画比值不同的比例感受一下,为后续学习打开一扇窗。瞻前顾后,复习课应做到上不封顶、下要保底。
如果将正、反比例的学习放在一个更上位的概念系统中看,应该是函数学习的一部分。因此,这一内容的学习应该是中学函数知识的前期准备,在这一准备中,应该有着后续学习所需要的“种子”,正如前期学习乘除法中的变化规律一样。在教学中我是这样渗透和铺垫的。首先通过《学习单》(图3)引导,画出的图象。
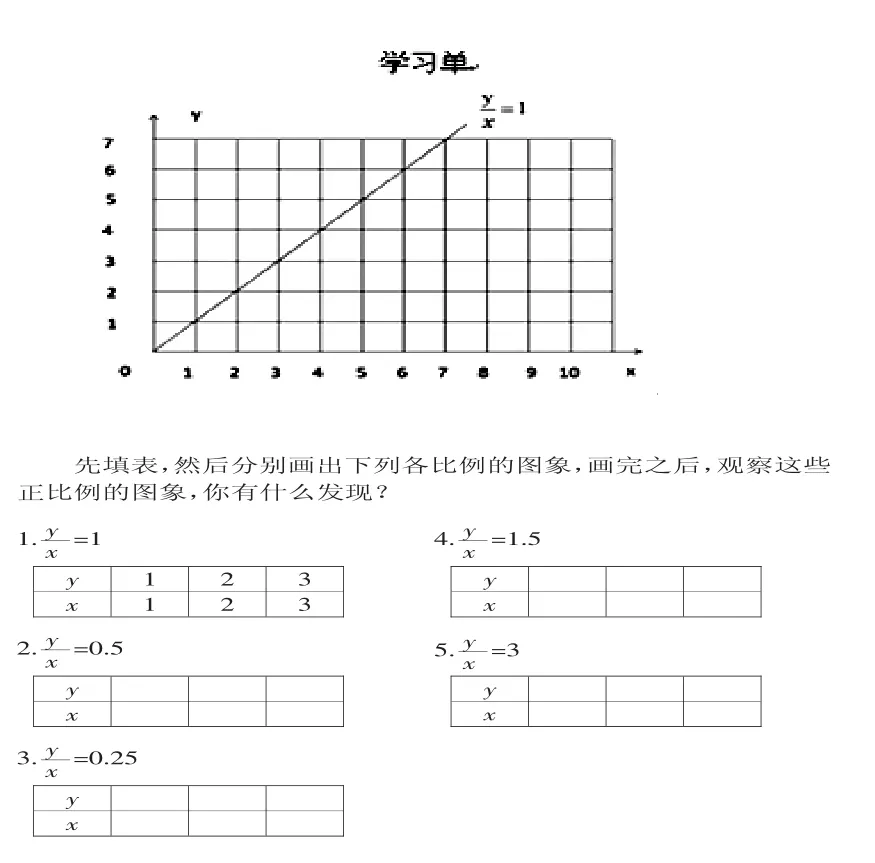
图3

图4
组织观察:这些直线有什么变化?你觉得与什么有关?学生发现直线的倾斜程度与比值有关。再引导学生聚焦直线的倾斜程度:倾斜程度的大小是从哪里看出来的?比值与夹角有什么样的关系呢?这些问题,让学生意识到正比例的价值,更激发了学生探究的欲望。重要的是让学生能对正比例产生问题,问题使结构常新,新的结构始终保持着一种开放的状态。
高观点下的复习整理,要整理、贯通,促使结构的生成。一是知识内部的联系紧密,加强知识之间的联系,从模型、本质的角度去理解知识,促使知识的“原来—现在—将来”能成为一个牢固的整体;二是不断在学生心中产生问题,保持结构的开放,使结构常新。
