热应力引发的轴颈中心位置测量误差分析
2021-03-26许泽玮杨建刚沈德明
许泽玮,杨建刚,沈德明
(1.东南大学 火电机组振动国家工程研究中心,南京 210096;2.南京科远智慧科技集团股份有限公司,南京 211102;3.江苏省热工过程智能控制重点实验室,南京 211102)
载荷对滑动轴承动力特性的影响较大,运行状态下轴承载荷状态可以根据轴颈中心位置判断。轴颈中心在轴承内位置低,说明载荷重;轴颈中心在轴承内位置高,说明载荷轻。因此,轴颈中心位置监测对分析和评判汽轮发电机组等采用滑动轴承的大型旋转机械的运行状态意义重大。
测量轴颈中心位置,需要在轴承上方左45°和右45°各布置一组电涡流传感器,测量静止、不同转速和不同工况下的间隙电压,由间隙电压变化量、传感器灵敏度和轴承间隙可计算得到轴颈在轴瓦内的位置[1]。电涡流传感器固定在轴瓦上,所测值为轴颈与轴瓦间距对应的间隙电压。因此,轴颈位置变化或轴瓦变形导致的传感器移动均会表现为轴颈中心位置变化。然而,目前监测轴颈中心位置时,大多不计轴瓦变形,认为探头到轴颈之间距离的变化仅由轴颈位置变化引起。实际上,轴瓦可以看成一个圆环,在力或温度场作用下,会产生变形。郭力等[2]研究了动静压轴承热变形,发现轴承径向热变形与油膜间隙处于同一数量级。于晓东等[3]研究了静压推力轴承的热变形,发现转速越高,热变形越大,热变形后工作台和底座形状均呈“碗状”。童宝宏等[4]研究了内燃机主轴承的热变形,发现热变形使轴心运动轨迹发生很大变化。岑黎明等[5]认为轴承在外力和自身热变形作用下会影响轴颈中心位置的测量精度,轴心位置测量应综合考虑间隙电压测量数据和轴压变形量的影响。
笔者建立滑动轴承流-固-热耦合动力学模型,计算不同状态下的油膜压力、温度场和轴瓦变形量,分析应力作用下轴瓦变形及其对轴颈中心位置测量值的影响,并以某滑动轴承为例,对某发电机组开机过程中轴颈中心位置的异常现象进行分析。
1 滑动轴承流-固-热耦合模型
图1给出了某滑动轴承结构图,该轴承由轴承座、垫片和轴瓦组成。轴瓦通过下部3块垫片支撑在轴承座上。垫片支撑方式使得轴瓦在轴承座内不受全周约束,轴瓦有变形空间。轴承水平中分面单侧设有供油管,润滑油由供油管流入油槽,由油槽进入轴承后向下流动润滑轴承,并从轴承两侧流出。
1.1 滑动轴承流场计算
润滑油在滑动轴承内的流动包含了气相和液相,引入基于Mixture模型的多相流模型,考虑润滑油在轴承内的两相流动效应[6]:

图1 滑动轴承结构图Fig.1 Structural diagram of sliding bearing
(1)
式中:vm为混合相质量平均速度;vk为第k相的速度;ρm为混合相密度;ηm为混合相黏度;vdr,k为第k相的相对漂移速度;μ0为润滑油初始黏度;T0为润滑油初始温度;T为某点处润滑油实际温度;b为常数;g为重力加速度;F为外部体积力;p为压力;Ek为第k相开口系的总能量;ρk为第k相的密度;SE为体积热源;t为时间。
边界条件为:
(2)
式中:pa为大气压力;pv为空化压力;z为转子轴向位置;l为转子轴向出口位置;Q为轴瓦与油膜的传热量;kl为润滑油传热系数;A为传热面积;Δt1为润滑油与轴瓦表面的温差。
求解滑动轴承流场时,网格划分采用规则六面体网格。兼顾精度和计算时间,在满足网格无关性前提下,轴向、周向和径向网格数分别为250、1 570和10,油膜下半部分网格的周向密度为上半部分的2倍[7]。图2给出了滑动轴承油膜计算域模型。

图2 滑动轴承油膜计算域模型Fig.2 Calculation domain model of sliding bearing oil film
1.2 轴瓦变形计算
轴瓦导热方程为:

(3)
式中:ρ为密度;H为显焓;v为速度;λ为导热系数。
热边界条件为:流固耦合面导入流场温度,垫片和轴瓦各外表面设为与环境导热,如图3所示。
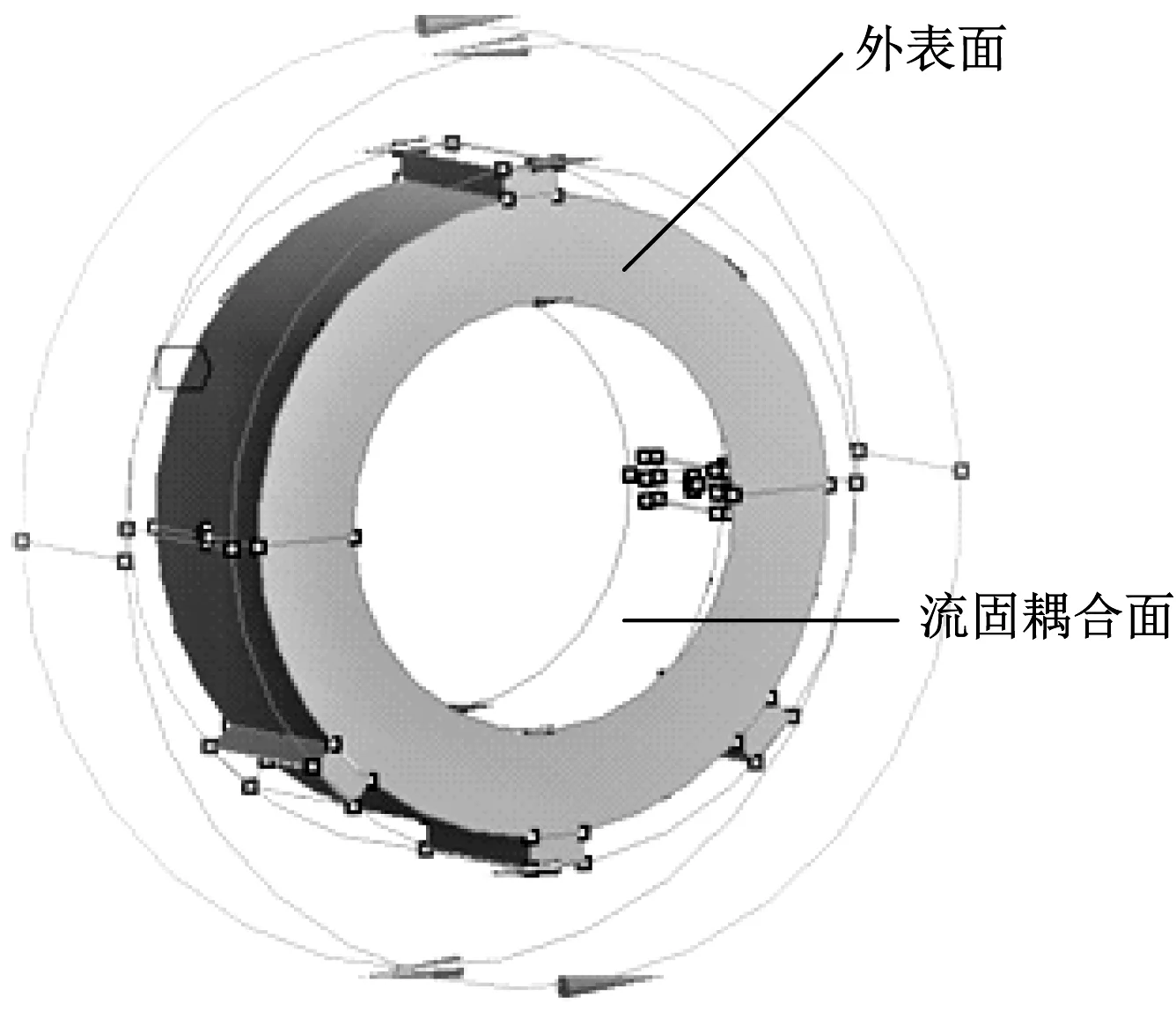
图3 热边界条件示意图Fig.3 Schematic diagram of thermal boundary conditions
热变形线性膨胀方程为:
ΔL=adΔt
(4)
式中:ΔL为温度变化Δt时的相对伸长量;a为线性热膨胀系数;d为直径。
弹性变形方程为:
σ=Dε
(5)
式中:σ为应力;D为弹性矩阵;ε为应变。
综上所述,在高校篮球运动发展的过程当中,如何解决当前存在的问题,是推动高校体育教师培养学生篮球运动发展最根本性的内容。因此,切实的从高校体育教师培养学生篮球运动的发展角度出发,对现存的问题进行解决,具有发展性的意义。
变形边界条件及轴承各部件间的连接方式如表1所示。

表1 各部件连接方式
2 轴承变形计算分析
以某滑动轴承为例,计算轴承温度、压力场及轴瓦变形情况,表2给出了轴承的计算参数[8]。

表2 轴承计算参数
2.1 滑动轴承内流场分析
图4~图6分别给出了滑动轴承油膜中空气体积分数分布、压力分布和温度分布[9]。

图4 轴承油膜中空气体积分数分布Fig.4 Air volume fraction distribution of bearing oil film
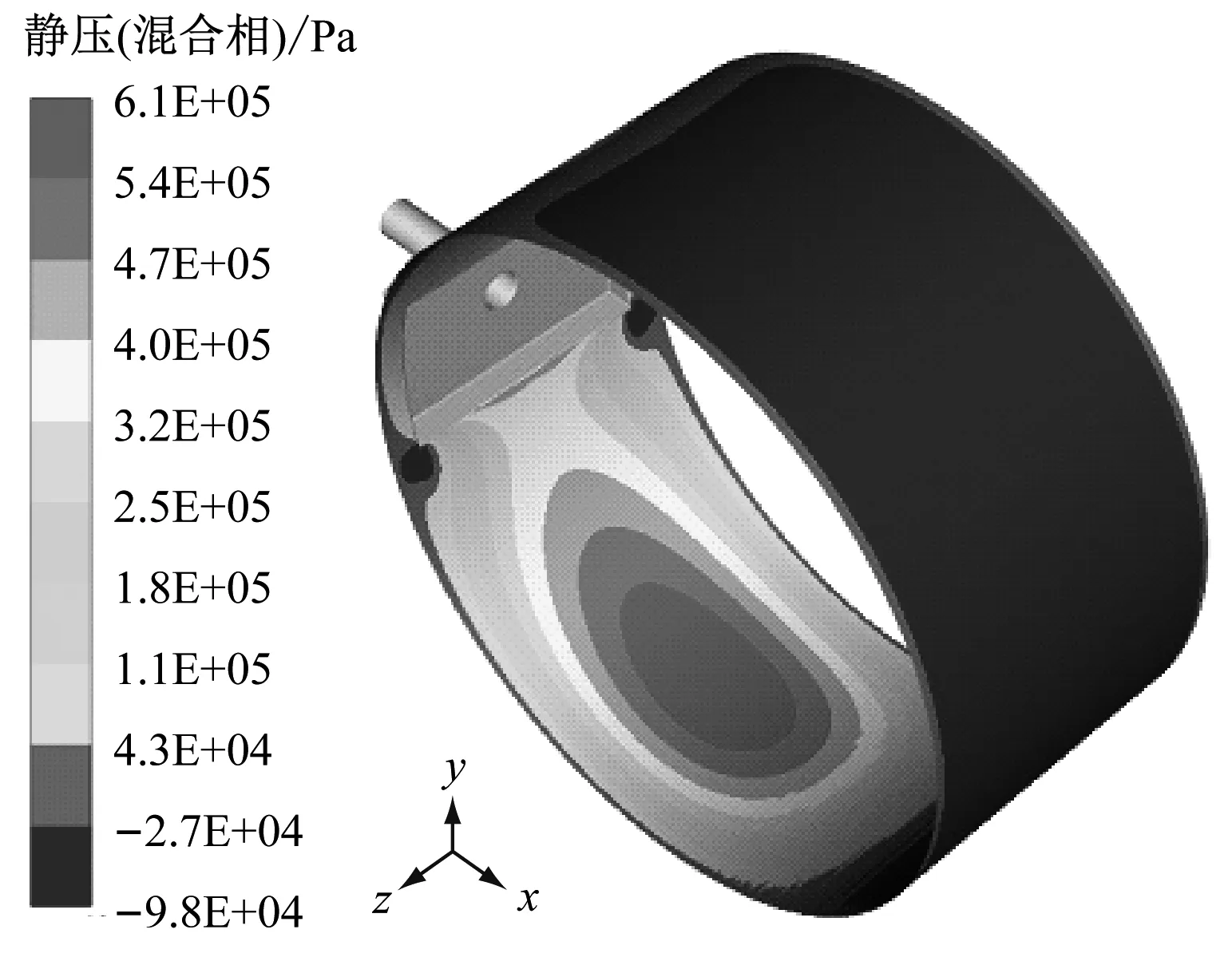
图5 轴承油膜压力分布Fig.5 Pressure distribution of bearing oil film
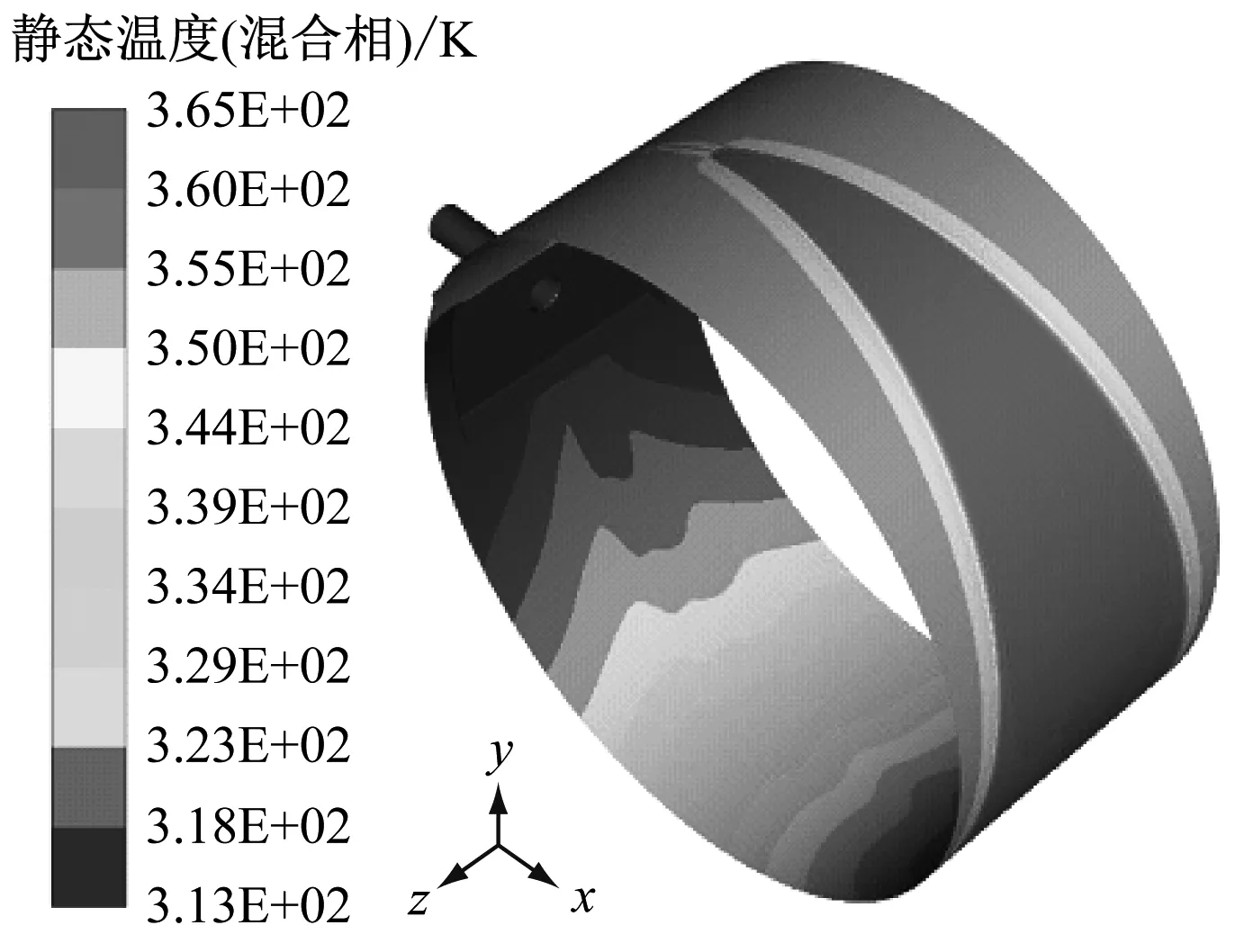
图6 轴承油膜温度分布Fig.6 Temperature distribution of bearing oil film
由图4、图5可知,收敛区内有完整油膜,油膜破裂边界呈现抛物线,汽化比例随着间隙的增大而增大,最大间隙上游附近油汽化比例达到最大。压力由进油口随转动方向逐渐增大,在最小间隙前达到最大值,之后压力随间隙的增大逐渐减小[10]。
从图6可以看出,油膜最高温度为92 ℃,最低温度为40 ℃,温差达52 K。热量产生的原因为黏性力做功。进油口顺着转动方向间隙变小,速度梯度变大,黏性力变大,做功变多,温度升高。产生的热量被流体沿着转动方向带走后,温度高点出现在最小间隙处沿转动方向之后。
图7给出了轴瓦的温度分布。从图7可以看出,油膜黏性剪切作用产生的热量为轴瓦温升热源,轴瓦温度分布规律与油膜温度分布规律一致。轴瓦内表面温差达到52 K。由于散热的影响,远离轴心方向的轴瓦温度分布不均匀情况逐渐缓解。
2.2 轴瓦变形分析
在温度场和压力场的作用下,轴瓦都可能产生变形,此处分别分析这2种因素对轴瓦的影响规律。
图8和图9分别给出了压力和温度作用下轴瓦的变形情况。由图8可知,压力作用下轴瓦变形为立式椭圆形,最大变形量位于进口油槽处,仅1.58 μm。
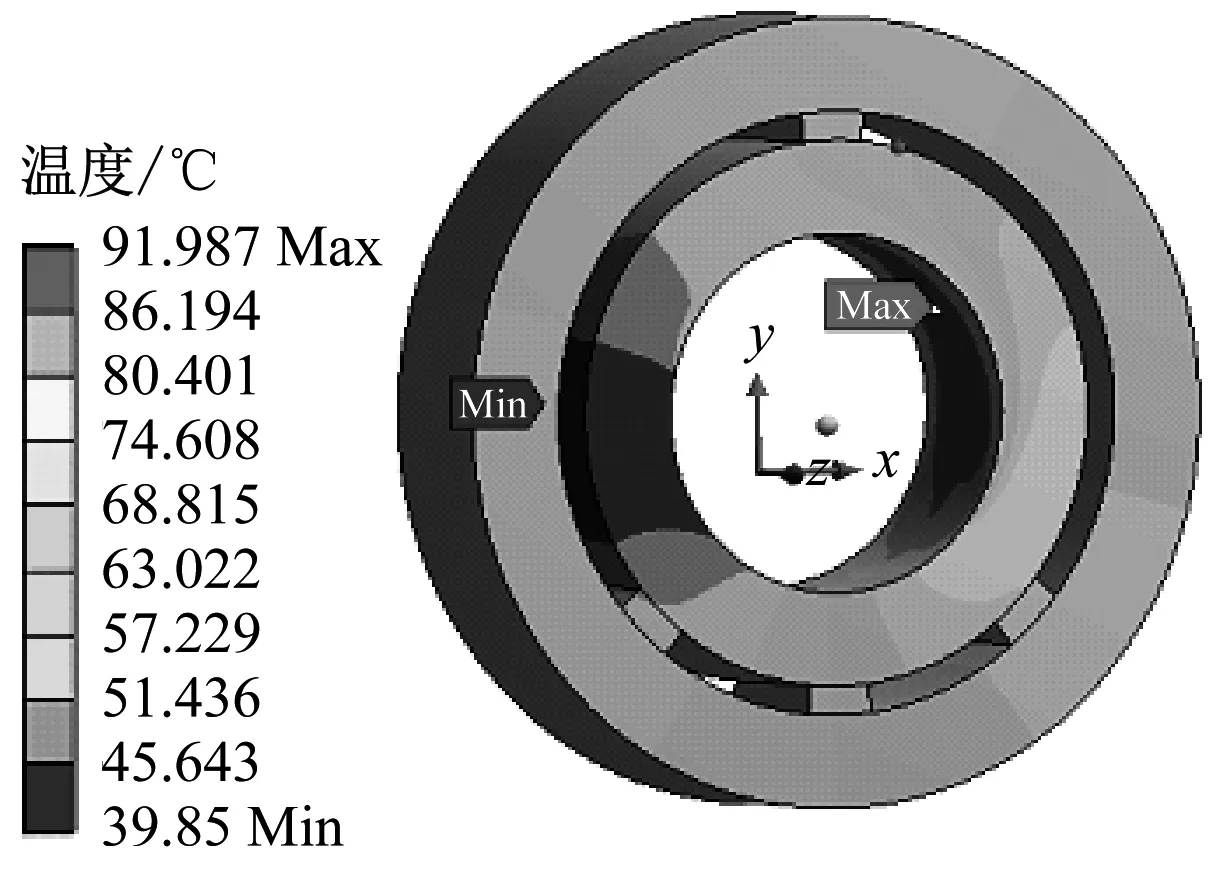
图7 轴瓦温度分布Fig.7 Temperature distribution of the bearing shell

图8 压力作用下的轴瓦总变形量Fig.8 Total deformation of the bearing shell under pressure
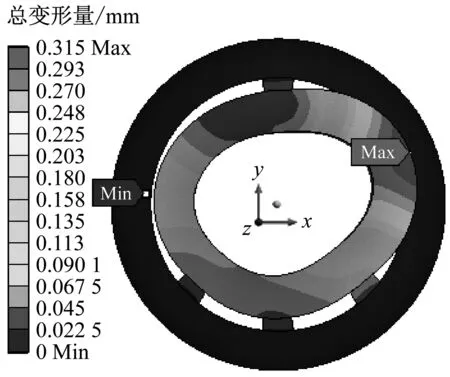
图9 温度作用下的轴瓦总变形量Fig.9 Total deformation of the bearing shell under temperature
由图9可知,温度作用下轴瓦内总变形量最大值为0.315 mm。受轴承上下4个垫片的约束和右上方温度高点热膨胀共同作用的影响,同时钢材变形时金属将沿着变形抵抗力最小的方向流动,故轴瓦向右上方凸出,变成不规则椭圆。
3 轴瓦变形引发的轴颈中心测量误差分析
如图10所示,轴瓦变形会导致轴颈中心位置测量误差。图中X、Y探头分别对应X、Y涡流传感器。
假设轴瓦变形前后,轴颈在轴瓦内的位置没有发生变化。图中M1、M2为X、Y涡流传感器的初始位置,C1、C2分别为X、Y涡流传感器的初始轴颈表面被测点,d1、d2分别为X、Y涡流传感器到轴颈表面的距离;上标*表示热变形后各点坐标。以表2所给参数为例,表3给出了热变形前后探头到轴颈表面距离的测量结果,其中,绝对误差为(d*-d),即轴瓦热变形后涡流传感器到轴颈表面距离与变形前的距离之差,相对误差为(d*-d)/d,即绝对误差与热变形前距离之比。
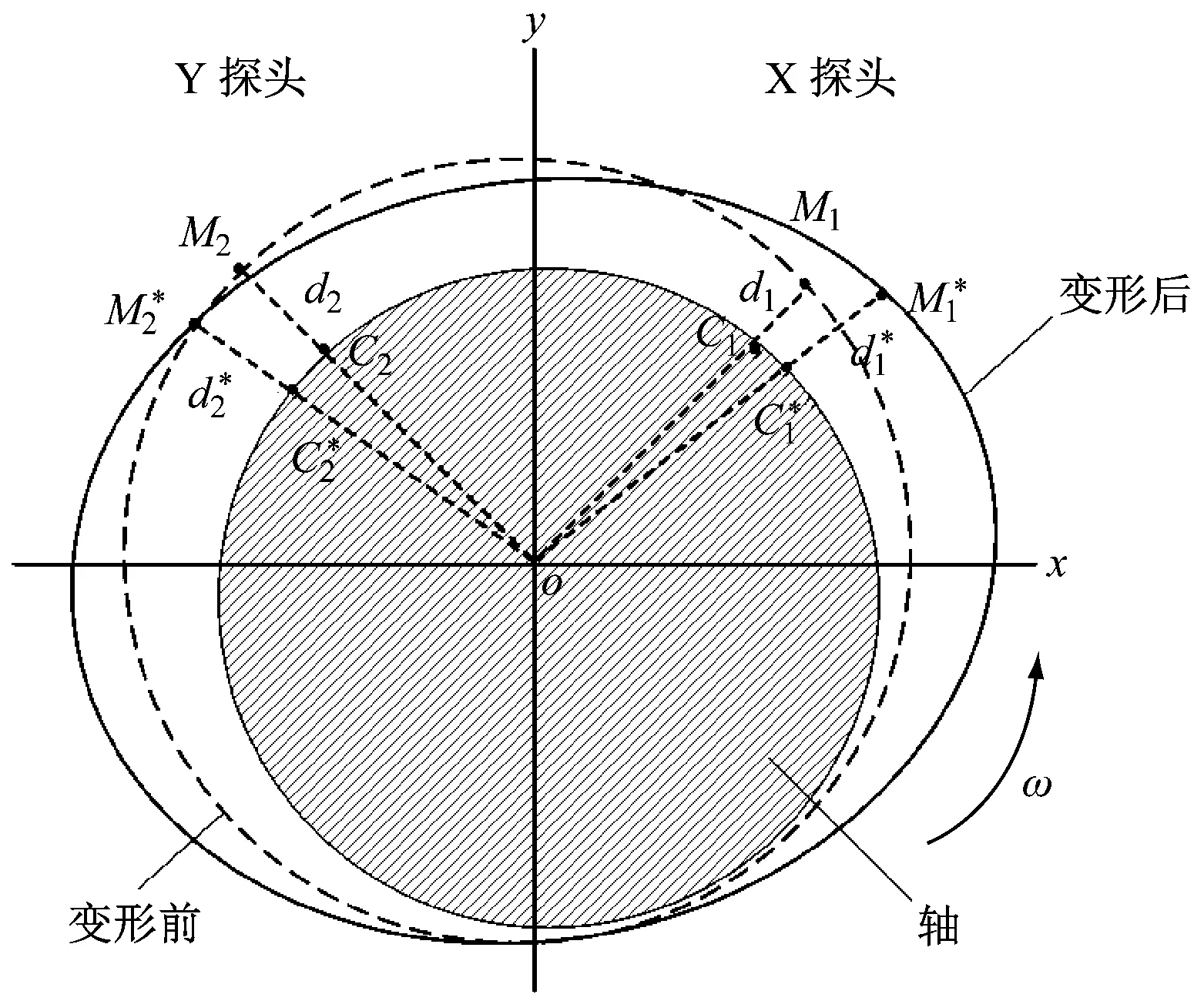
图10 轴瓦变形前后轴颈中心位置测量示意图

表3 涡流传感器测量误差
从表3可以看出,X探头方向的相对误差为30.48%,Y探头方向的相对误差仅为2.76%。受轴瓦热变形的影响,导致X探头随轴瓦向远离轴颈表面方向移动了0.171 9 mm,会得到轴颈向X探头所指方向移动了0.171 9 mm的错误判断。
4 工程实例
图11给出了某厂一台重型燃气轮机在开机过程中实测3号轴承X、Y涡流传感器的间隙电压随转速的变化情况。
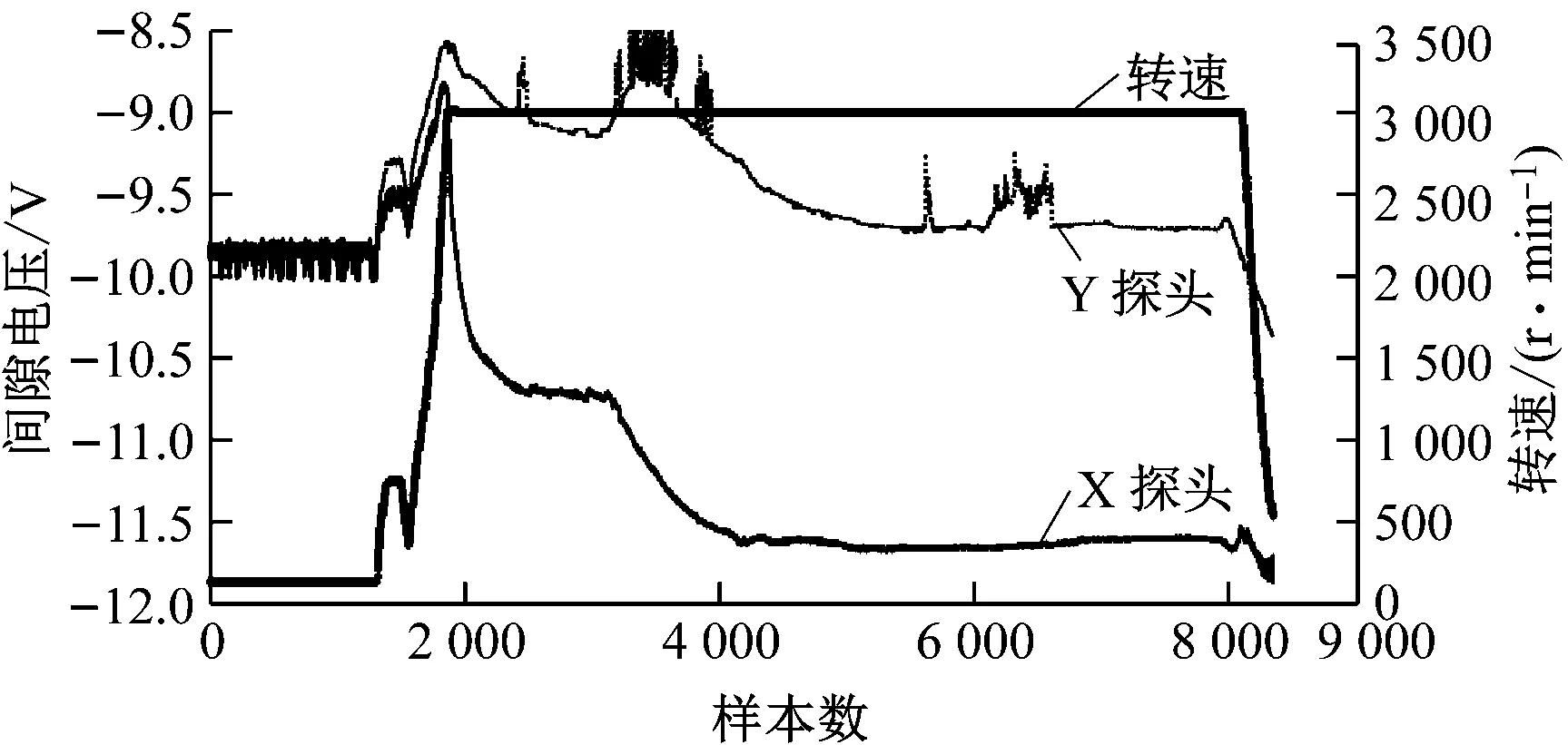
图11 X、Y涡流传感器间隙电压随转速的变化Fig.11 Variation of X, Y probe gap voltage with speed
图12给出了升速过程中不同转速和工况下轴颈中心位置的变化情况。初始盘车转速下轴颈位于轴瓦底部,此时X、Y探头到轴颈表面距离最大。转速从0 r/min到3 000 r/min过程中,油膜力不断增大,轴颈逐渐上升,轴颈中心位置变化比较规则。3 000 r/min后,随着运行时间的延长,轴颈中心位置逐渐向左下方移动,直至超出轴承半径间隙圆。但由于轴瓦的约束,轴颈不可能离开轴瓦,故任何时候间隙电压绝对值均不应大于初始状态下的值,此时X探头间隙电压绝对值却大于初始状态下的值,这种现象在实际工程中是不会发生的。
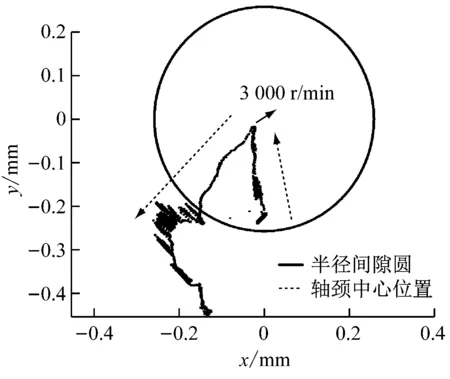
图12 轴颈中心位置随转速的变化Fig.12 Variation of journal center position with speed
分析表明,随转速的提升,X探头所处位置温度逐渐升高,轴瓦逐渐热膨胀,固定在轴瓦上的涡流传感器随之外移,使得涡流传感器与轴瓦之间距离增大,得出轴颈离开轴瓦的错误结论。
5 结 论
(1) 在温度和压力的作用下轴瓦都能产生变形,但温度是导致轴瓦变形的主要因素,压力的影响较小。
(2) 轴瓦热变形对轴颈中心位置测量结果的影响较大,若不考虑轴瓦热变形,轴颈中心位置测量相对误差最大达到30.48%,因此对轴承状态分析的影响不可忽略,该现象值得重视。
