基于动态论域的循环流化床锅炉燃烧系统的模糊自适应PID控制

李丰泽，马素霞

(太原理工大学 电气与动力工程学院，太原 030024)

循环流化床(CFB)技术是清洁煤燃烧技术之一[1]。由于CFB锅炉燃烧系统自身非线性、大延时、多变量耦合的特点，目前的燃烧自动控制系统投入率低，尤其是在机组负荷调整过程中，锅炉主要参数处于不断震荡的状态，过调与回调交替进行，燃烧系统无法稳定运行[2]。

针对以上问题，笔者提出燃烧系统模糊自适应比例积分微分(PID)控制，根据各燃烧参数的动态调整进程，通过模糊推理实时修定PID参数。同时，考虑到CFB锅炉燃烧系统工况变化大，控制全程使用固定的模糊论域，难以取得良好的控制精度，因此引入时变论域的概念，旨在不改变模糊整定规则的前提下，利用伸缩因子对模糊论域范围进行调整，更精准地整定不同工况的PID参数，实现CFB锅炉燃烧系统全工况优良的控制性能[3]。

1 CFB锅炉燃烧系统的解耦

1.1 CFB锅炉燃烧系统控制特性

CFB锅炉燃烧系统是一个非线性、大滞后、多变量强耦合的被控对象[4]。燃烧状态易受负荷扰动、煤质扰动等影响，造成燃烧系统运行不稳定[5]。由于炉内循环物料量大，CFB锅炉燃烧控制过程普遍存在很大的延时，输入量的响应过程较长，这样的大滞后特性很容易造成各燃烧参数的震荡。最重要的是，CFB锅炉燃烧系统的控制对象众多，且相互之间关联耦合严重，调整一个输入量会影响多个被控对象，动态特性复杂，大大增加了控制的难度。图1为CFB锅炉各变量之间的耦合关系。

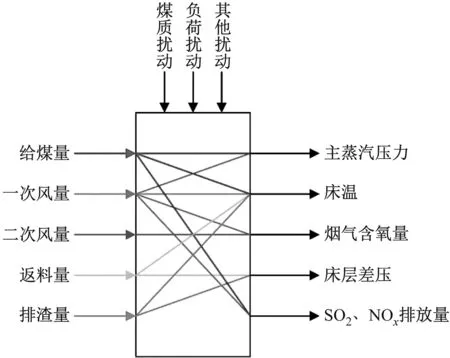
图1 燃烧系统的变量关联耦合示意图Fig.1 Diagram of variable correlation coupling ofcombustion system

其中，床温与主蒸汽压力共同受多个输入变量的影响，耦合程度最严重[6]。作为CFB锅炉稳定运行最重要的2个参数，床温不仅直观地反映了炉内热量的供需关系，而且合适的床温有利于提高炉内脱硫脱硝效率，减少SO2和NOx排放；主蒸汽压力则直观反映了机组负荷指令的跟进效果[7]。床温和主蒸汽压力一般通过一次风量和给煤量进行调节，但存在一次风量逆向调节现象和给煤量调节延迟大等问题，传统模糊PID控制方法无法获得良好的控制性能。笔者设计了前馈补偿解耦控制器和基于动态论域的模糊自适应PID控制器，对CFB锅炉床温和主蒸汽压力的控制性能进行了仿真研究。

1.2 CFB锅炉燃烧系统建模

目前，建立CFB锅炉燃烧系统的模型主要有2种方式：一类是基于流化床燃烧传热特性结合能量守恒、物料守恒建立机理模型，另一类是根据现场阶跃试验结果，由被控参数的响应曲线拟合建立回路间的传递函数模型，或者基于机组历史运行数据利用神经网络等工具建立智能模型[8]。

参阅文献[9]，以某CFB锅炉为研究对象，基于机理建模与现场试验验证，得到100%工况下床温和主蒸汽压力关于一次风量、给煤量的复域传递函数矩阵模型：

(1)

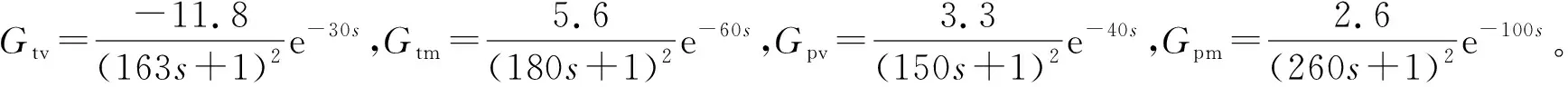
式中：Tb、p0分别为床温和主蒸汽压力；V1、M分别为一次风量和给煤量；Gtv、Gtm、Gpv、Gpm为各回路的传递函数，这些传递函数均已被验证适用于该锅炉75%～110%的负荷范围；s为拉普拉斯算子。

1.3 前馈补偿解耦控制

由于床温与主蒸汽压力之间的强耦合作用，一般的控制方法难以发挥作用，消解耦合是改进控制策略的前提。确定二者与一次风量、给煤量的最佳配对是解耦控制系统设计的基础。马素霞等[10]基于相对增益分析理论(RGA理论)对CFB锅炉燃烧系统各输入输出变量间的影响进行了分析，结果表明调门开度和燃烧率对主蒸汽压力的影响占据主导；一次风量与床温的相对增益最大。因此，选择给煤量作为主蒸汽压力的主调节量，一次风量作为床温的主调节量。

采用前馈补偿法实现床温与主蒸汽压力的解耦，前馈补偿解耦结构图如图2所示，其中T0、T分别为床温的设定值和实际值，p为主蒸汽压力的实际值，C1、C2为解耦后2个独立回路的控制器，U1、U2为2个控制器的输出值，D21、D12为前馈补偿解耦控制器的传递函数。

针对此次进博会，汇丰在中国首次推出全新的数字化贸易融资服务，利用移动通讯技术，让客户可以加快国际贸易交易过程，加强现金流管理并优化供应链管理，从而提高他们的市场竞争力。

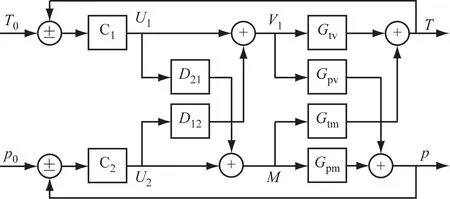
图2 前馈补偿解耦结构图Fig.2 Structure diagram of the feed-forwardcompensation decoupling

根据前馈补偿解耦原理，为消除一次风量-床温、给煤量-主蒸汽压力2个回路的耦合关系，解耦控制器的传递函数模型为：

(2)

在Matlab的Simulink环境中搭建前馈补偿解耦控制系统模型，通过给煤量对主蒸汽压力进行单位阶跃仿真，对比解耦前后床温的响应输出。同理，通过一次风量对床温进行单位阶跃仿真，对比解耦前后主蒸汽压力的响应输出。仿真结果表明，应用解耦策略后，主蒸汽压力与床温的关联耦合明显减弱，形成一次风量-床温、给煤量-主蒸汽压力2个基本独立的控制回路，满足下文动态论域模糊自适应PID控制的设计需求。

2 动态论域模糊自适应PID控制器

2.1 动态论域模糊自适应PID控制器结构设计

随着机组负荷工况的变化，CFB锅炉燃烧系统的数学模型也在不断变化，呈现非线性、动态时变的复杂特性。传统模糊PID控制虽然兼具PID控制简洁性和模糊控制模糊性特质，可针对大惯性、时变系统制定有效的控制策略，但其存在模糊论域、模糊控制规则固定以及模糊变量数量有限等局限性，对于工况变化范围大的CFB锅炉燃烧系统，无法兼顾调节速度和控制精度，控制效果往往不佳[11]。为克服上述局限性，引入时变模糊论域的概念，通过改变伸缩因子对模糊论域进行实时自适应调整，以获得全工况优良的控制性能。图3为模糊论域变化示意图，其中α(t)为伸缩因子在控制过程中随时间的变化；E代表模糊控制的初始论域范围，模糊推理器输入与输出变量均以正大(PB)、正中(PM)、正小(PS)、零(ZO)、负小(NS)、负中(NM)和负大(NB) 共7个语言值进行模糊子集划分。

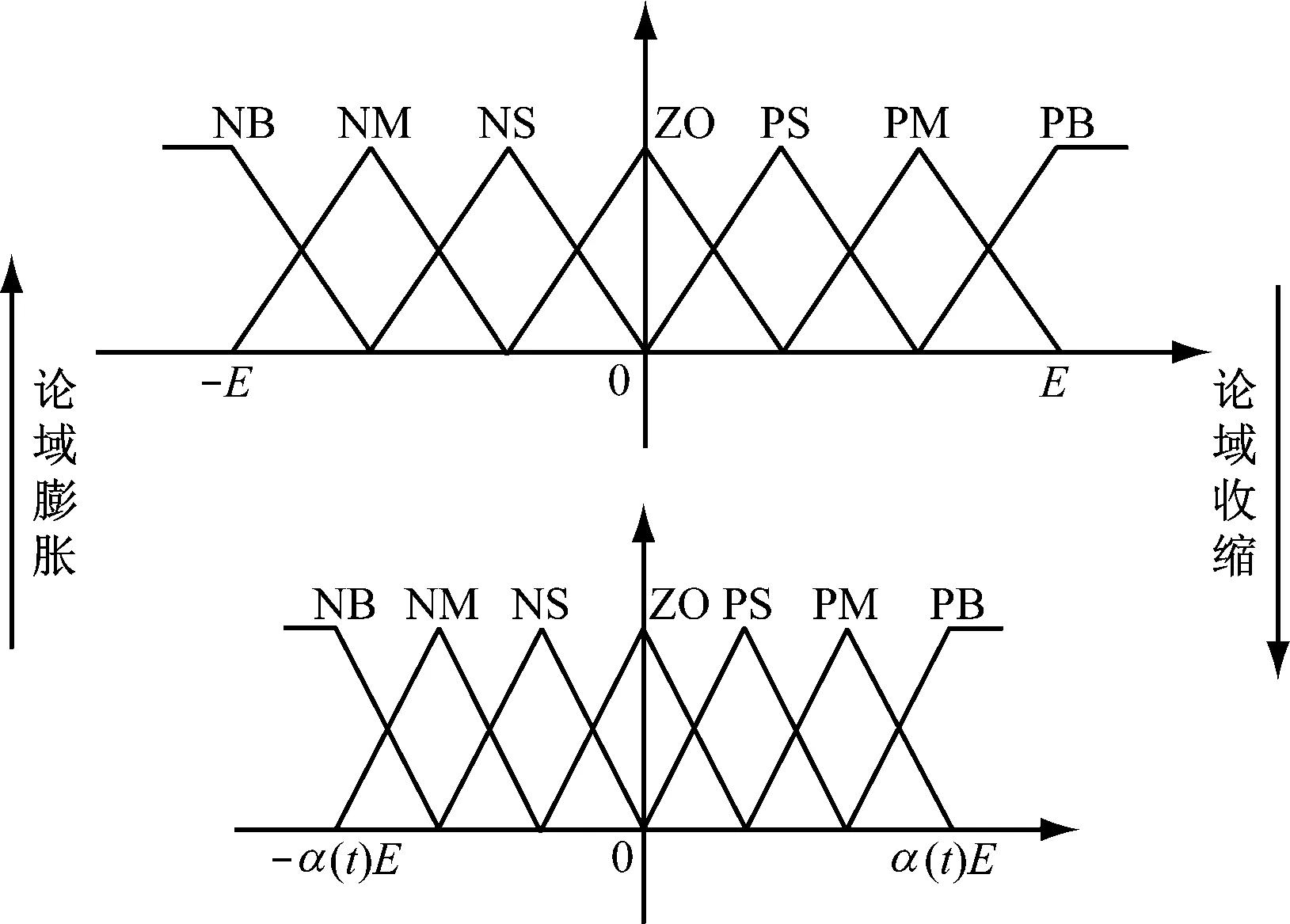
图3 模糊论域变化示意图Fig.3 Diagram of fuzzy universe change

当误差e与误差变化率ec随控制作用逐渐缩小时，如仍使用初始论域[-E,E]，则模糊控制规则触发次数减少，导致控制过程粗糙。若通过伸缩因子α∈[0,1]将论域缩小为[-αE,αE]，虽然模糊变量数量不变，但零点附近单位论域上的模糊变量划分密集，相当于间接增加了模糊控制规则，提高了控制的灵敏度。同理，当初始控制阶段误差e和误差变化率ec较大时，可通过伸缩因子α∈(1,+∞)将论域膨胀为(-αE,αE)，有利于加速系统响应，减少调节时间[12]。

笔者所设计的二维动态论域模糊自适应PID控制，依据输入的误差e和误差变化率ec进行2次自适应参数整定。第一次由伸缩因子函数对伸缩因子进行整定，自适应调节模糊论域范围；第二次根据模糊控制规则在适当范围内对PID参数进行细调修正，满足不同阶段的控制需求。CFB锅炉动态论域模糊自适应PID控制系统的结构见图4。

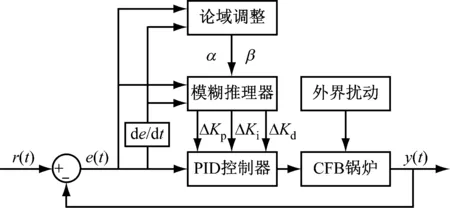
图4 动态论域模糊自适应PID控制系统结构图Fig.4 Structure diagram of dynamic universe fuzzyadaptive PID control system

图4中，r(t)、y(t)分别为被控变量设定值和实际值；论域调整采用双输入双输出结构，输入值为误差e(t)和误差变化率ec(t)，输出值α、β为模糊论域伸缩因子；模糊推理器输出量ΔKp、ΔKi、ΔKd为PID控制器3个参数的修正量。

2.2 论域调整规则

伸缩因子的设计主要有2种方法：基于函数形式设计和基于模糊推理设计。参阅文献[11]，输入变量误差e(t)和误差变化率ec(t)的论域伸缩因子α1和α2的函数为：

(3)

ΔKp、ΔKi、ΔKd的论域伸缩因子β1、β2和β3的函数均为：

(4)

式中：φ1、φ2和φ3为常数，可防止模糊论域伸缩因子趋近于0。

2.3 模糊推理隶属度函数选择

综合CFB锅炉燃烧系统特性与热工现场控制精度需求，针对不同工况和误差e(t)分别制定隶属度函数规则，在偏离设定值较大的区域{NB,NM}、{PM,PB}选取分辨率相对较低的Gauss型隶属度函数，可以提高系统的鲁棒适应性；在设定值附近的区域{NS,ZO,PS}选取分辨率高的Trimf型隶属度函数，可以更好地兼顾燃烧控制的灵敏性和精准性。考虑到控制系统的稳定性，误差变化率ec(t)和ΔKp、ΔKi、ΔKd均选用Trimf型隶属度函数。

2.4 模糊控制规则

以给煤量-主蒸汽压力回路为例来说明模糊控制规则制定原则。

(1) 当主蒸汽压力偏离设定值超过5%，且误差继续升高或无明显变化时，由于CFB锅炉的大滞后特性，比例常数kp应适当增大以加快系统响应，阻止主蒸汽压力的误差继续扩大，与此同时，考虑到燃烧系统的大热惯性，为防止出现长时间积分累计引起大幅度超调，积分常数ki与微分常数kd应取值较小。

(2) 当主蒸汽压力偏离设定值1%～5%，且误差减小时，说明控制系统正在起作用，此时应减小kp，在保证收敛速度的同时防止出现过调现象，同时ki和kd应取值适中。

(3) 当主蒸汽压力偏离设定值小于1%时，取较大的kp和ki可提高控制稳定性和精准性，同时考虑到CFB锅炉的大惯性特点，防止主蒸汽压力在目标值附近震荡，出现过调与回调不断交替的现象，kd应适当取小。

基于以上PID控制器参数调整原则，结合热工现场实际操作经验，制定模糊控制规则表(见表1)。根据表1采用Mamdani法进行推理，得到PID参数修正量的模糊量矩阵，使用加权平均法将其清晰化为PID参数的实际修正量。将实际修正量ΔKp、ΔKi、ΔKd与经粒子群算法基于误差绝对积分(ITAE值)最小原则寻优得到的初始设定PID参数Kp0、Ki0、Kd0求和，可得到调整后的PID参数Kp、Ki、Kd。

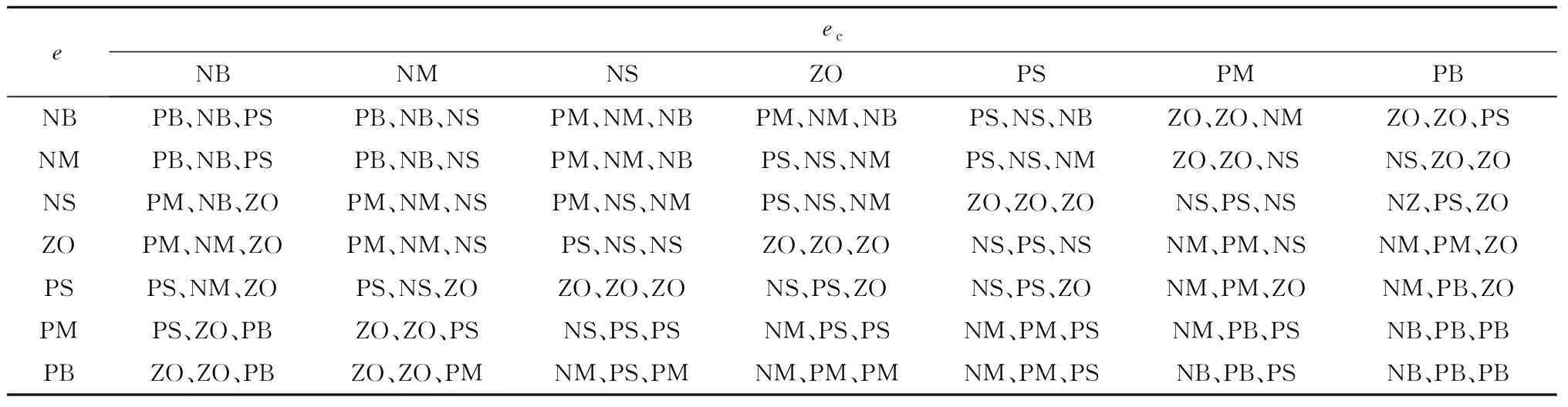
表1 ΔKp、ΔKi、ΔKd模糊控制规则表

3 系统仿真结果与分析

为验证所设计的控制器性能，在Matlab的Simulink环境下，建立CFB锅炉燃烧系统动态论域模糊自适应PID控制系统模型，同时将模糊控制模型以及初始参数相同的模糊PID控制模型设为对照组进行分析对比。给煤量-主蒸汽压力回路的具体模型见图5。

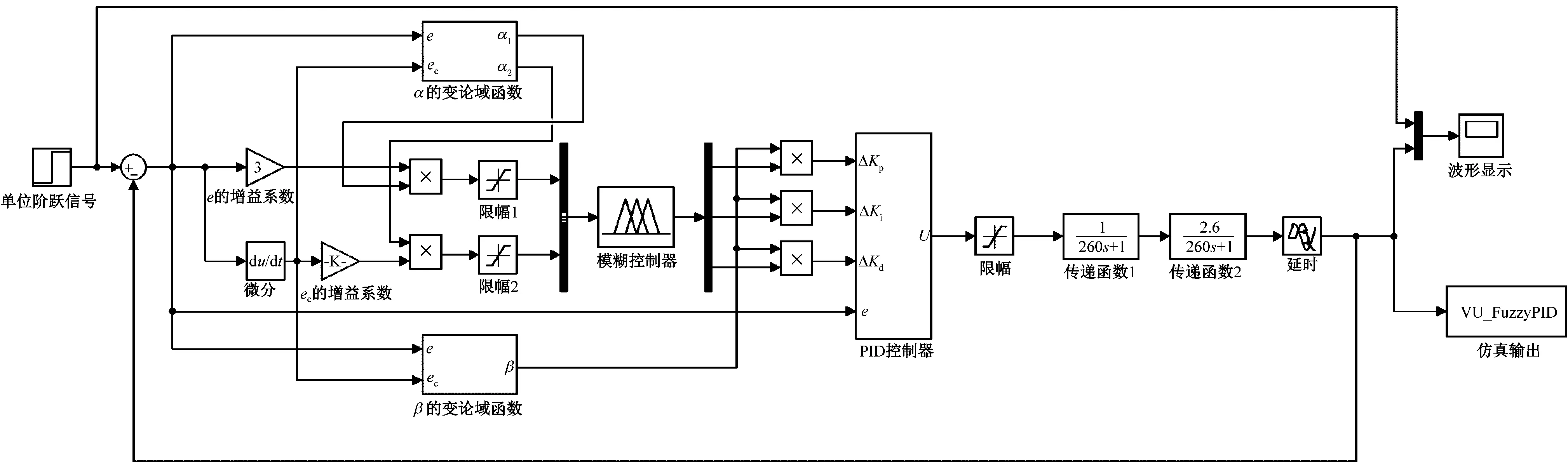
图5 Matlab系统仿真模型

3.1 设定值跟踪试验

首先进行床温和主蒸汽压力设定值跟踪试验，输入信号选择单位阶跃信号，采样周期为0.01 s，仿真时间为2 500 s，3种控制器的动态响应曲线见图6和图7。

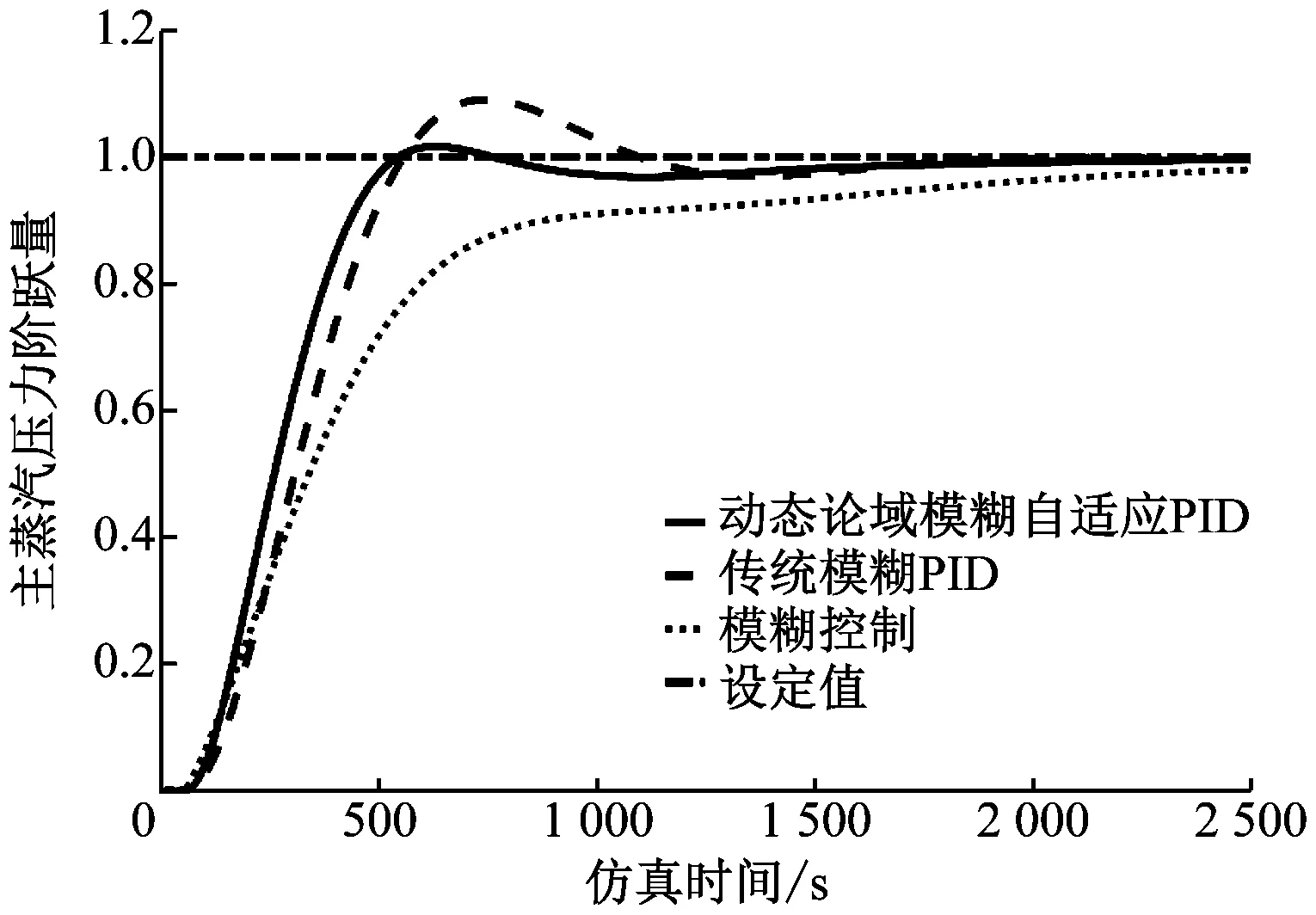
图6 主蒸汽压力阶跃响应仿真曲线Fig.6 Step response curve of main steam pressure by simulation

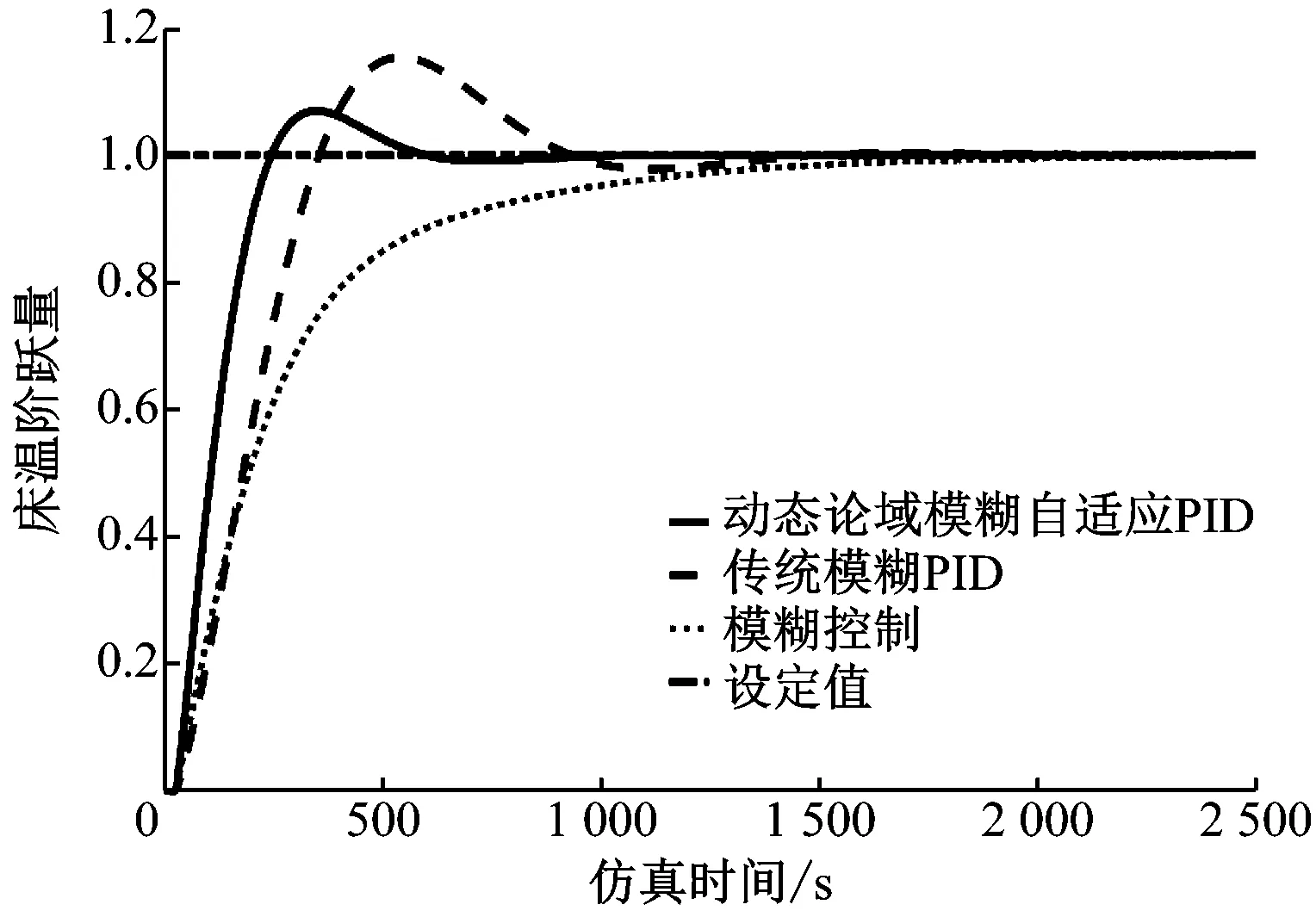
图7 床温阶跃响应仿真曲线Fig.7 Step response curve of bed temperature by simulation

根据图6、图7、表2和表3可知，与传统模糊PID控制器相比，针对CFB锅炉燃烧系统特性设计的动态论域模糊自适应PID控制器的动态响应速度提高近30%，动态超调量减小5%～10%；与模糊控制器相比，动态论域模糊自适应PID控制器的动态响应速度提高50%，具有收敛速度快、稳态精度高的优势；动态论域模糊自适应PID控制的ITAE值远小于其他控制方法，也证明了其优越的综合控制性能。

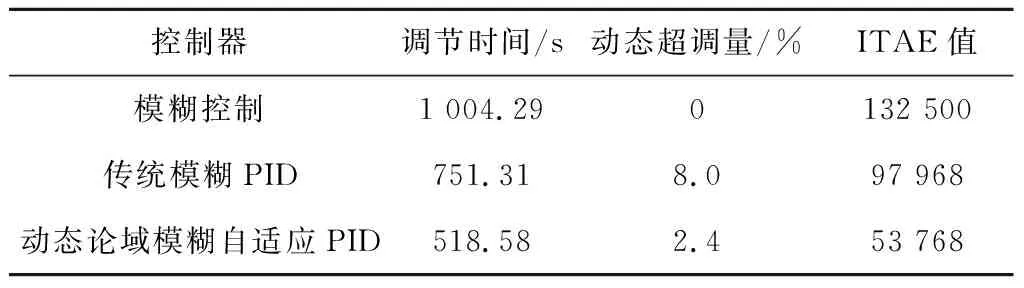
表2 主蒸汽压力曲线的动态性能指标

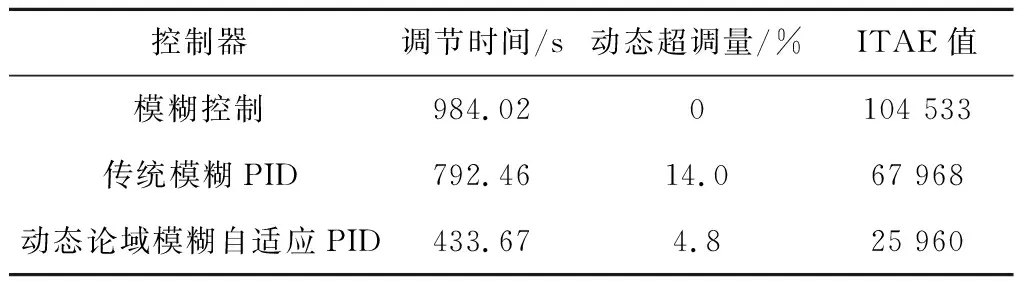
表3 床温曲线的动态性能指标

3.2 鲁棒稳定性分析试验

随着工况的变化，CFB锅炉燃烧系统模型参数变化较大，将其控制系统应用于实际热工现场时，必须进行鲁棒稳定性分析试验[10]。基于Mente-Carlo原理，依据100%工况的标称传递函数矩阵模型，通过参数不确定性假设，将模型中容易发生变化的增益系数、惯性常数基于标称值发生±20%随机扰动，扰动值大小服从均匀分布，使用随机生成的不确定模型进行1 000次随机仿真试验，对控制系统的鲁棒性能进行分析研究。

图8为参数随机扰动下，主蒸汽压力和床温的调节时间(曲线不再超出±5%误差带所需的最小时间)与动态超调量分布情况的散点图。

由图8可知，在参数随机扰动±20%的情况下，主蒸汽压力和床温的调节时间和动态超调量均较小，且分布较为集中，说明动态论域模糊自适应PID控制器具有较强的鲁棒性，能够满足实际热工现场需求。

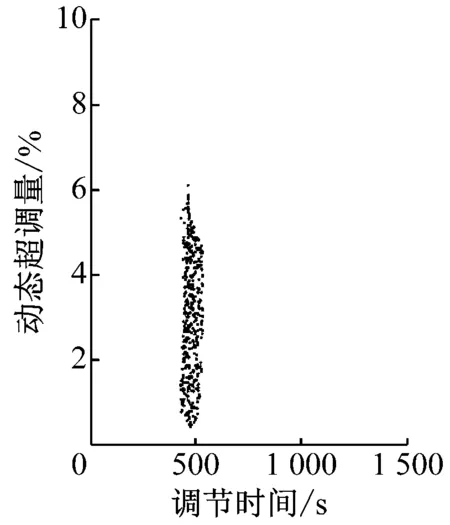
(a) 主蒸汽压力(b) 床温图8 动态论域模糊自适应PID控制系统鲁棒性能分析Fig.8 Robustness property analysis of the fuzzy adaptive PID control system based on dynamic universe

4 结 论

针对CFB锅炉主蒸汽压力与床温强耦合的特点，采用前馈补偿解耦控制器能够有效减弱两者之间的耦合作用。相较于传统模糊PID控制、模糊控制，基于动态论域的模糊自适应PID控制系统响应速度快，动态超调量小，稳态精度高。燃烧系统模型参数不确定性试验结果表明，该控制器具有较强的自适应性和鲁棒性。