超临界压缩空气堆积床蓄冷罐循环性能分析
2021-03-26陈梦东徐桂芝邓占锋廖志荣
陈梦东,徐桂芝,胡 晓,邓占锋,廖志荣
(1.全球能源互联网研究院有限公司,北京 102209;2.华北电力大学 能源动力与机械工程学院,北京 102206)
随着电网中风能、光伏等可再生能源电力的大规模接入,如何克服这些新能源电力间歇性和波动性带来的冲击成为高比例可再生能源电网的关键问题。大规模储电技术是解决这一问题的重要途径。在目前众多的储电技术中,只有抽水蓄能和压缩空气储能(CAES)能够提供高于100 MW的独立储电容量[1]。传统CAES系统存在过度依赖化石燃料和大型储气室的缺点,因此其大规模的应用推广受到限制。为了克服这些缺点,各国学者们相继开发了新的CAES系统,如绝热CAES(A-CAES)、小型CAES(SS-CAES)、液体空气蓄能(LAES)和超临界CAES(SC-CAES)[2-4]。其中,SC-CAES的储能密度可达340 MJ/m3,效率达到67%,具有广阔的发展前景[5-6]。
蓄冷换热器是SC-CAES的关键部件之一。现有研究表明堆积床蓄冷罐可用作蓄冷换热器,其蓄冷介质为岩石颗粒,可直接与空气接触进行冷能的存储[7]。在系统储电(堆积床蓄冷罐释冷)过程中,来自压缩机的常温超临界空气自上而下流过堆积床蓄冷罐,被低温岩石冷却成具有超临界压力的深冷液态空气。在系统放电(堆积床蓄冷罐储冷)过程中,来自低温泵的超临界压力深冷液态空气进入堆积床,并被岩石加热成常温超临界空气。可见,该堆积床蓄冷罐运行过程中最显著的特征是其传热流体在超临界状态下工作。目前,在A-CAES、SC-CAES和LAES系统中,以超临界流体为传热流体的堆积床得到了国内外学者的关注[8-10]。
刘佳[11]的研究结果表明,超临界压力下空气与岩石之间的温差远低于低压下的温差。Chai等[12]搭建了堆积床低温蓄冷实验装置,通过实验发现在超临界压力下堆积床中的温度分布与大气压下的温度分布有很大不同。Morgan等[13]提出了一种蜂窝存储的概念,其中单个蓄冷模块可以串联、并联或独立工作,从而可灵活地改变蓄冷过程中的高宽比以适应能量储存速率,其分析表明,与单一储存模块相比,多模块的设计可以实现更高的系统效率。Hüttermann等[14]的研究结果表明,LAES系统储冷介质的比热容对蓄冷罐效率具有显著影响,并推荐了聚乙烯、聚丙烯、氯化钠和石英石4种深冷储冷介质。李国跃等[15]的实验结果表明,上千次循环后岩石的密度、导热系数和比热容无明显变化。李良星等[16]通过实验研究了砂石颗粒堆积床内的流动特性,结果表明小尺寸砂石颗粒堆积床的两相流动阻力压降随着气相雷诺数的增大呈现上升趋势,相间摩擦力对两相流动阻力有重要影响。
通过以上分析可以发现,针对采用超临界流体的堆积床蓄冷系统循环热性能的研究很少。与采用非超临界流体作为传热流体的堆积床蓄冷罐不同,采用超临界压缩空气作为传热流体的堆积床蓄冷罐,其释冷过程中空气由超临界状态变为液态,储冷过程正好相反,跨临界的变化使压缩空气的热物性急剧变化,从而影响堆积床蓄冷罐性能,但出口截断温度、入口质量流量和蓄冷罐内工作压力等关键参数对堆积床蓄冷罐性能的影响尚不清晰。针对这一问题,笔者采用数值模拟方法研究了采用超临界压缩空气作为传热流体的堆积床蓄冷罐的储释冷动态过程。采用二维热平衡模型对采用超临界压缩空气作为传热流体的堆积床蓄冷罐内储释冷循环过程进行了模拟计算,分析了传热流体出口截断温度、入口质量流量和蓄冷罐内工作压力等关键参数对堆积床蓄冷罐性能的影响。
1 模型及其验证
图1为典型的堆积床蓄冷罐(以下简称蓄冷罐)的储释冷过程示意图,其中岩石作为蓄冷介质,超临界压缩空气作为传热流体。在蓄冷罐的上下出口各安装一个均流器,用以使空气均匀流过蓄冷罐内部的颗粒。在释冷过程中,具有超临界压力的常温空气被泵入蓄冷罐顶部,与岩石颗粒换热并被带走热量,从而变成超临界液态空气,最后从底部流出。在储冷过程中,超临界压力下的液态空气被泵入蓄冷罐底部,将冷能释放到岩石中,最后从顶部流出。
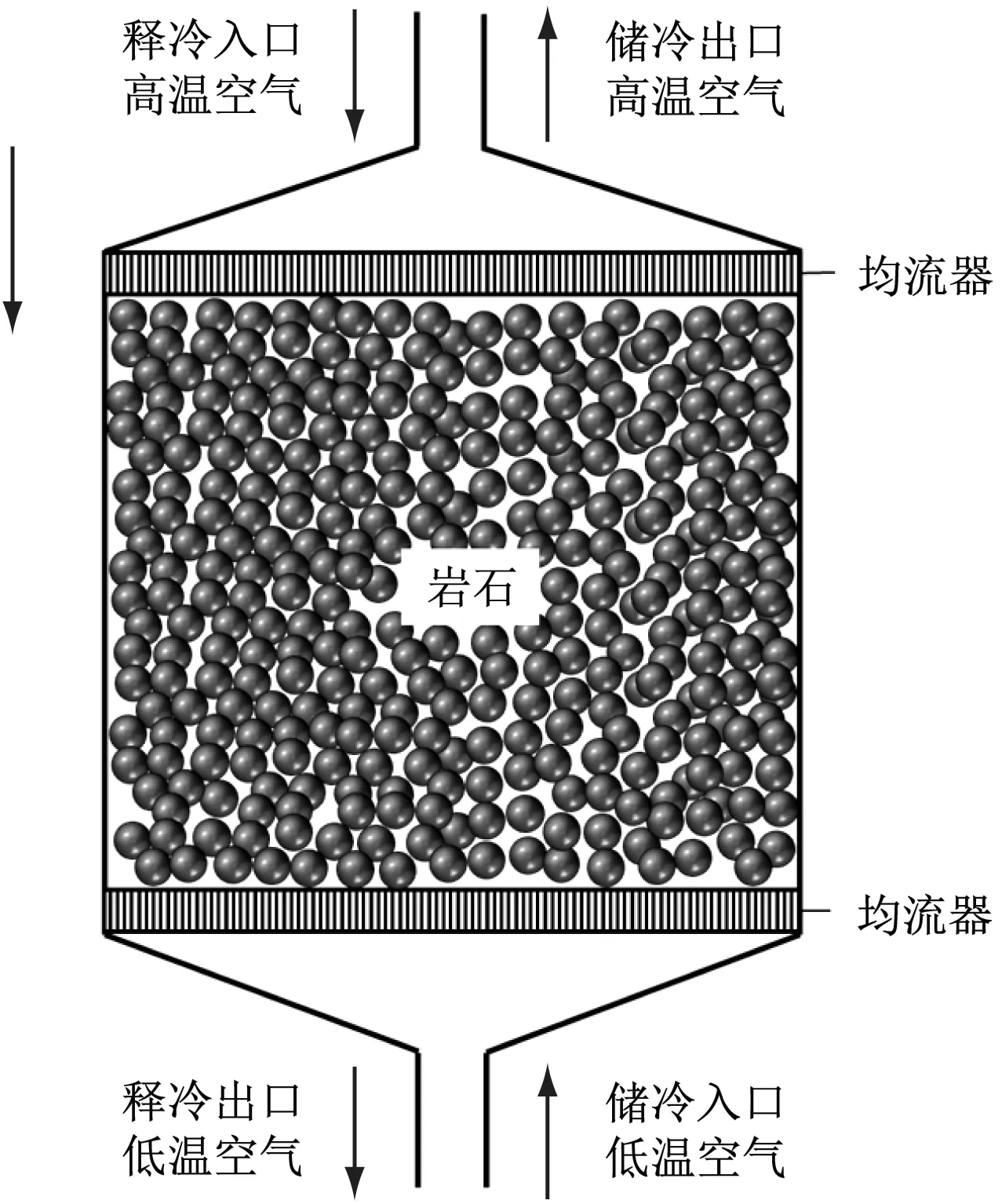
图1 堆积床蓄冷罐示意图(无保温材料)Fig.1 Schematic of the packed bed cold energy storagetank (without adiabatic material)
在模型建立过程中,进行如下假设:固体岩石颗粒各向同性,直径相同,蓄冷罐内岩石颗粒孔隙均匀,蓄冷罐沿轴线呈轴对称结构;2个均流器设计良好,以保证空气均匀流入堆积床区域,因此这2个分流器不计入计算区域;罐体采用绝热材料,隔热良好,绝热材料外表面作为绝热壁面处理;忽略传热流体和固体颗粒之间的温差。基于上述假设,计算域被简化为二维轴对称模型,如图2所示,图中rb为蓄冷罐半径;Hb为蓄冷罐轴向高度。
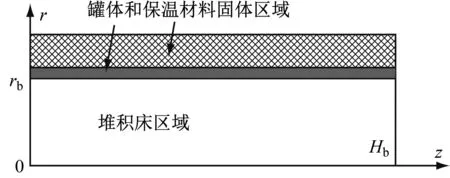
图2 堆积床蓄冷罐物理模型Fig.2 Physical model of the packed bed cold energy storage tank
一般情况下,蓄冷罐多孔区域内压缩空气的流动状态可通过雷诺数Re确定[17]:
(1)
式中:ρl、v和μ分别为传热流体的密度、表观速度和动力黏度;dp为固体颗粒的直径。
本文研究的传热流体雷诺数小于300,因此蓄冷罐内的流动可以作为层流处理。采用多孔介质模型处理堆积床多孔区域,其连续性方程为:
(2)
式中:ε为孔隙率;u为传热流体的速度矢量;t为时间。
采用Brinkman-Forchheimer扩展的Darcy定律模拟堆积床多孔流动,其动量方程为:
(3)
式中:g为重力加速度;p为传热流体的压力;K为表征多孔介质内部渗透性的系数;F为多孔介质惯性阻力系数。
固体颗粒和传热流体的能量方程为:
(4)
式中:keff=εkl+(1-ε)ks;cp,l为传热流体的比热容;cp,s为固体颗粒的比热容;kl为传热流体的导热系数;ks为固体颗粒的导热系数;T为温度;ρs为罐体和保温材料的密度。
罐体和保温材料固体区域的能量方程为:
(5)
式中:cp为罐体和保温材料的比热容。
针对半径为0.4 m、高度为4.0 m的堆积床蓄冷罐进行分析,罐体厚度为1.6 cm。保温材料为膨胀珍珠岩,厚度为20 cm。储释冷循环过程中的初始条件和循环工况参考文献[5]。蓄冷罐内岩石初始温度为87.2 K,绝热材料的外表面在储释冷过程中为绝热边界条件。在释冷过程中,入口位于蓄冷罐顶部,采用质量流量入口边界(释冷过程传热流体质量流量qm,dis,in=0.3 kg/s),温度为300 K,出口位于底部,蓄冷罐的工作压力pdis为13.0 MPa。在储冷过程中,传热流体入口位于底部,采用质量流量入口边界(储冷过程传热流体质量流量qm,ch,in=0.3 kg/s),温度为81.9 K,顶部为压力出口边界,蓄冷罐的工作压力pch为7.0 MPa。
本文计算中石块密度为2 668 kg/m3,低温下石块的比热容和导热系数与温度有关,来源于文献[12]和文献[18]。罐体壳壁由不锈钢制成,其密度、比热容和导热系数依次为8 000 kg/m3、502 J/(kg·K)和16.0 W/(m·K)。绝热材料是膨胀珍珠岩,其密度、比热容和导热系数分别为55 kg/m3、750 J/(kg·K)和0.023 W/(m·K)。传热流体超临界压力空气的物性与温度和压力相关,采用NIST实际气体模型(PEFPROP)进行计算[19],结果见图3。由图3可知,在储释冷过程中空气的密度、黏性系数和导热系数均随着温度的升高而急剧下降。空气比热容则在空气临界点温度附近由于相变的发生而产生剧变,出现峰值,且该峰值随着压力的升高而下降。
针对上述循环工作条件,所研究的蓄冷罐中岩石颗粒的理论最大储冷容量为420 MJ,空气的理论最大储冷容量为20 MJ,因此空气仅占蓄冷罐理论最大储冷容量的4.5%。循环过程中判断蓄冷罐是否达到可重复循环稳定状态的依据为:当前后2次循环过程中储释冷截止时刻蓄冷罐温度的相对误差在0.1%以内。
在蓄冷罐储释冷循环过程中,随着斜温层逐渐往出口处移动,储冷过程的蓄冷罐出口温度逐渐降低,释冷过程的蓄冷罐出口温度逐渐升高,使得储释冷效率越来越低。因此,为了避免储释冷效率过低,实际运行时在储冷过程中当蓄冷罐出口温度下降到储冷截止温度Tch,cut时便停止储冷,释冷过程中当蓄冷罐出口温度上升到释冷截止温度Tdis,cut时停止释冷。参照文献[20],引入储释冷截断因子Rch和Rdis来分析储释冷截止温度、储冷入口温度和释冷入口温度的关系,其定义如下:
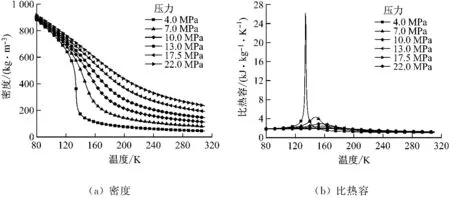
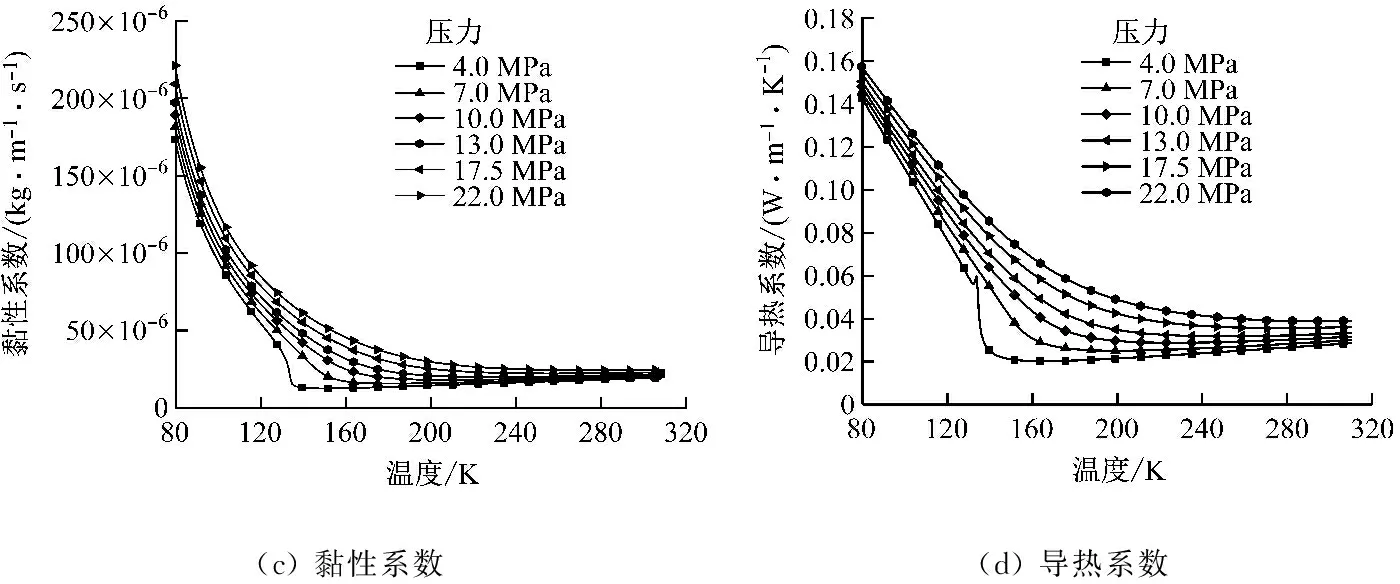
图3 不同压力下超临界压缩空气密度、比热容、黏性系数和导热系数随温度的变化Fig.3 Density, thermal capacity, viscosity and thermal conductivity of supercritical compressedair vs.temperature at different pressures
Tdis,cut=Tdis,high-Rdis(Tdis,high-Tch,low)
(6)
Tch,cut=Tch,low+Rch(Tdis,high-Tch,low)
(7)
式中:Tdis,high为释冷过程入口传热流体温度;Tch,low为储冷过程入口传热流体温度。
为了对循环过程中蓄冷罐的效率进行分析,引入有效容量比来描述实际蓄冷罐储冷容量与蓄冷罐最大理论储冷容量之比,其表达式如下:
(8)
N=εVtank(ρair,dishair,dis-ρair,chhair,ch)
式中:qm,ch,out和hch,out分别为储冷时出口质量流量与焓;hch,in为储冷时入口焓;tch为储冷进行时间;Vtank为蓄冷罐体积;cp,rock为储冷介质的比热容;ρrock为储冷介质的密度;ρair,dis和hair,dis分别为释冷过程空气的密度和焓;ρair,ch和hair,ch分别为储冷过程空气的密度和焓。
利用有限体积法离散计算域[21],控制方程的空间离散均具有二阶精度。采用SIMPLE算法求解上述控制方程,在计算过程中,连续性、速度和能量方程的收敛标准分别为10-3、 10-3和10-6。经过网格和时间步长无关解计算发现17 400个网格和0.4 s的时间步长在收敛区域内,且误差小于1%,因此将其用于本文研究中。
2 结果与验证
2.1 模型验证
为了验证本文模型的可靠性,使用上述数值模型来计算参考文献[11]和参考文献[12]中蓄冷罐的储冷过程。在文献所述的实验中,超临界液氮(温度为103 K,压力为6.5 MPa)流进高温堆积床中,被岩石颗粒加热而变成超临界液氮(液氮的临界点温度约为126 K,压力约为3.4 MPa)。在模型验证计算过程中,堆积床的尺寸、初始条件、边界条件以及液氮和岩石的物性均与参考文献[11]和参考文献[12]中相同。图4给出了不同时间下本文模型计算所得轴向温度分布与实验数据的比较。图中,T1、T3、T5、T7指沿蓄冷罐轴向不同位置的温度。由图4可以看出,模型计算结果与实验数据吻合较好,说明本模型可用于计算蓄冷罐储释冷过程中的流动与传热,其中堆积床内传热流体在超临界压力流体和超临界流体2种状态之间发生相变。
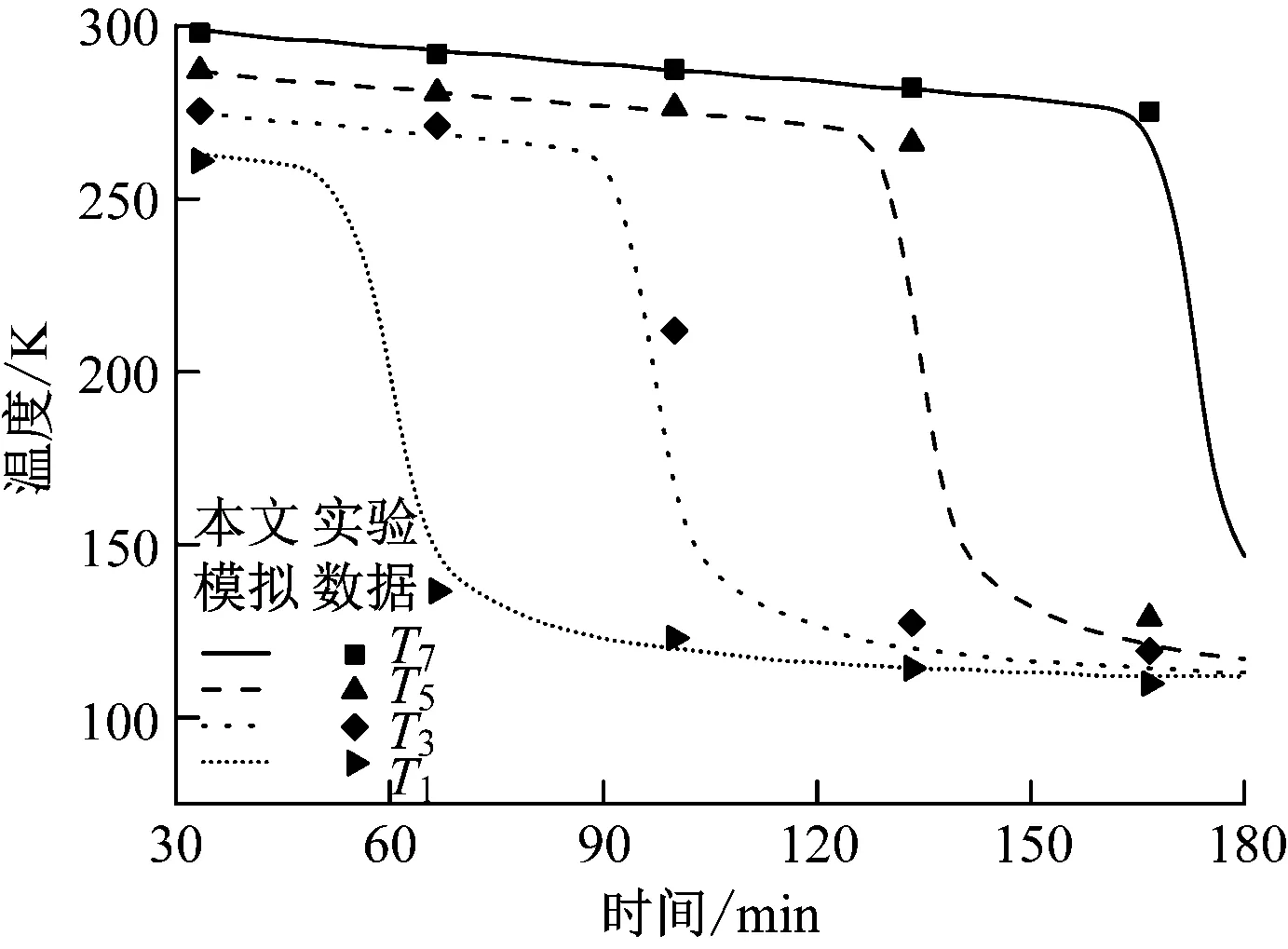
图4 本文模型计算所得轴向温度分布与实验数据的比较
2.2 截断因子的影响
首先分析截断因子对达到可重复循环状态下蓄冷罐储释冷性能的影响。利用上述模型模拟了储释冷截断因子(Rch=Rdis)分别为0.75、 0.8、 0.85、0.9 和0.95 5种工况下的循环过程。这5种工况的储释冷质量流量均为0.3 kg/s,储冷工作压力为7.0 MPa,释冷工作压力为13.0 MPa。图5给出了蓄冷罐达到可重复循环状态下,储释冷截断因子由0.75变化到0.95时,储释冷过程中蓄冷罐出口空气温度、储释冷时间和循环时间的变化。由图5可以看出,不同截断因子下储释冷过程中蓄冷罐出口空气温度具有一致的变化趋势,并且不同截断因子的蓄冷罐出口空气温度之间差距非常小。随着储释冷截断因子由0.75增大到0.95,储冷时间由103 min上升到124 min,释冷时间由116 min上升到168 min,循环时间由219 min提高到292 min。随着截断因子的增大,储释冷时间和循环时间的增长速率逐渐变大,且释冷时间的增长速率高于储冷时间的增长速率。
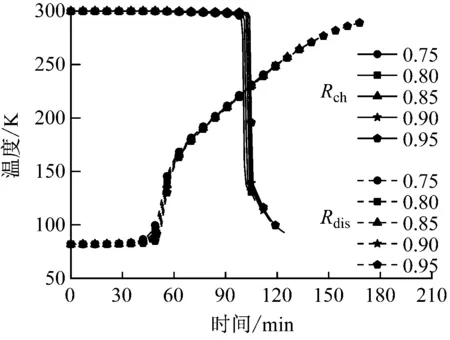
(a) 储释冷过程中蓄冷罐出口空气温度变化
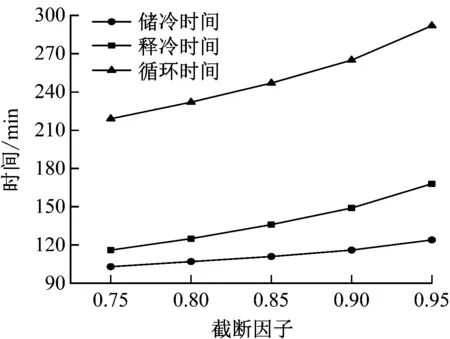
(b) 储释冷时间和循环时间图5 不同储释冷截断因子时可重复循环状态下各性能参数的变化(1)
图6给出了不同储释冷截断因子时可重复循环状态下储释冷截止时刻蓄冷罐轴向温度分布和有效容量比,图中Z表示沿蓄冷罐轴向距离底部的距离。由图6可知,随着截断因子的增大,储释冷截止时刻蓄冷罐内斜温层厚度减小,释冷截止时刻蓄冷罐出口处的温度升高,同时储冷截止时刻蓄冷罐出口处的温度降低。因此,蓄冷罐储释冷截止时刻轴向温差越大,这导致蓄冷罐存储的冷量增加,有效容量比ηcr从89.9%增大到98.4%。但是,总体上当储释冷截断因子大于0.75时,蓄冷罐的有效容量比均在90%以上。
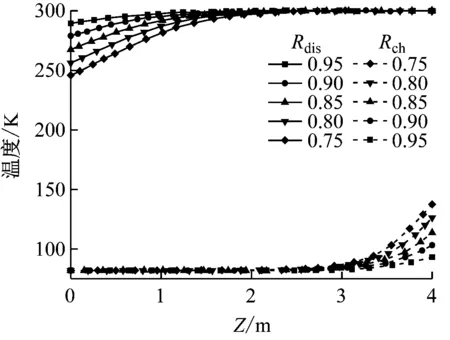
(a) 储释冷截止时刻蓄冷罐轴向温度分布
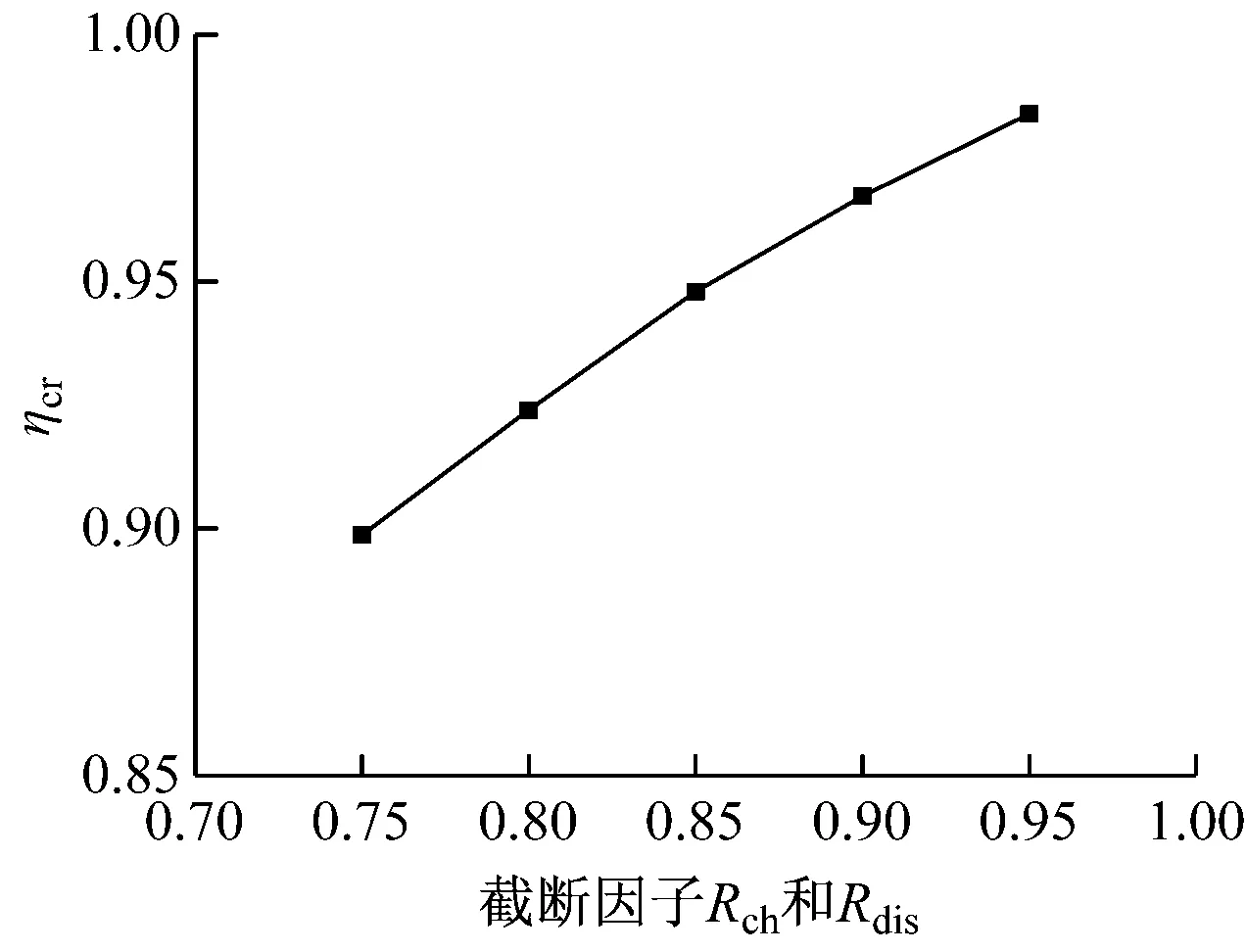
(b) 有效容量比ηcr图6 不同储释冷截断因子时可重复循环状态下各性能参数的变化(2)
2.3 储释冷质量流量的影响
本小节分析储释冷过程中压缩空气质量流量(即储释冷质量流量)对蓄冷罐循环性能的影响,模拟计算了5种不同储释冷质量流量(qm,ch,in=qm,dis,in, 即0.1 kg/s、 0.2 kg/s、 0.3 kg/s、 0.4 kg/s和0.5 kg/s)工况下蓄冷罐的循环过程。这5种工况的储释冷截断因子均为0.85,储冷工作压力为7.0 MPa,释冷工作压力为13.0 MPa。
图7给出了不同储释冷质量流量时可重复循环状态下储释冷过程中蓄冷罐出口空气温度、储释冷时间和循环时间的变化。由图7可以看出,不同储释冷质量流量下储释冷过程的出口温度变化趋势一致。随着储释冷质量流量从0.1 kg/s上升到0.5 kg/s,储冷过程中恒定出口空气温度时间段从296 min缩短到60 min,释冷过程中恒定出口空气温度时间段从140 min缩短到28 min。储释冷循环中储冷时间从418 min下降到81 min,释冷时间从335 min下降到66 min,循环时间则从753 min下降到147 min。储释冷质量流量增大时,储释冷时间减小幅度基本一致。但是随着储释冷质量流量的提高,储释冷时间和循环时间的缩短幅度减小。
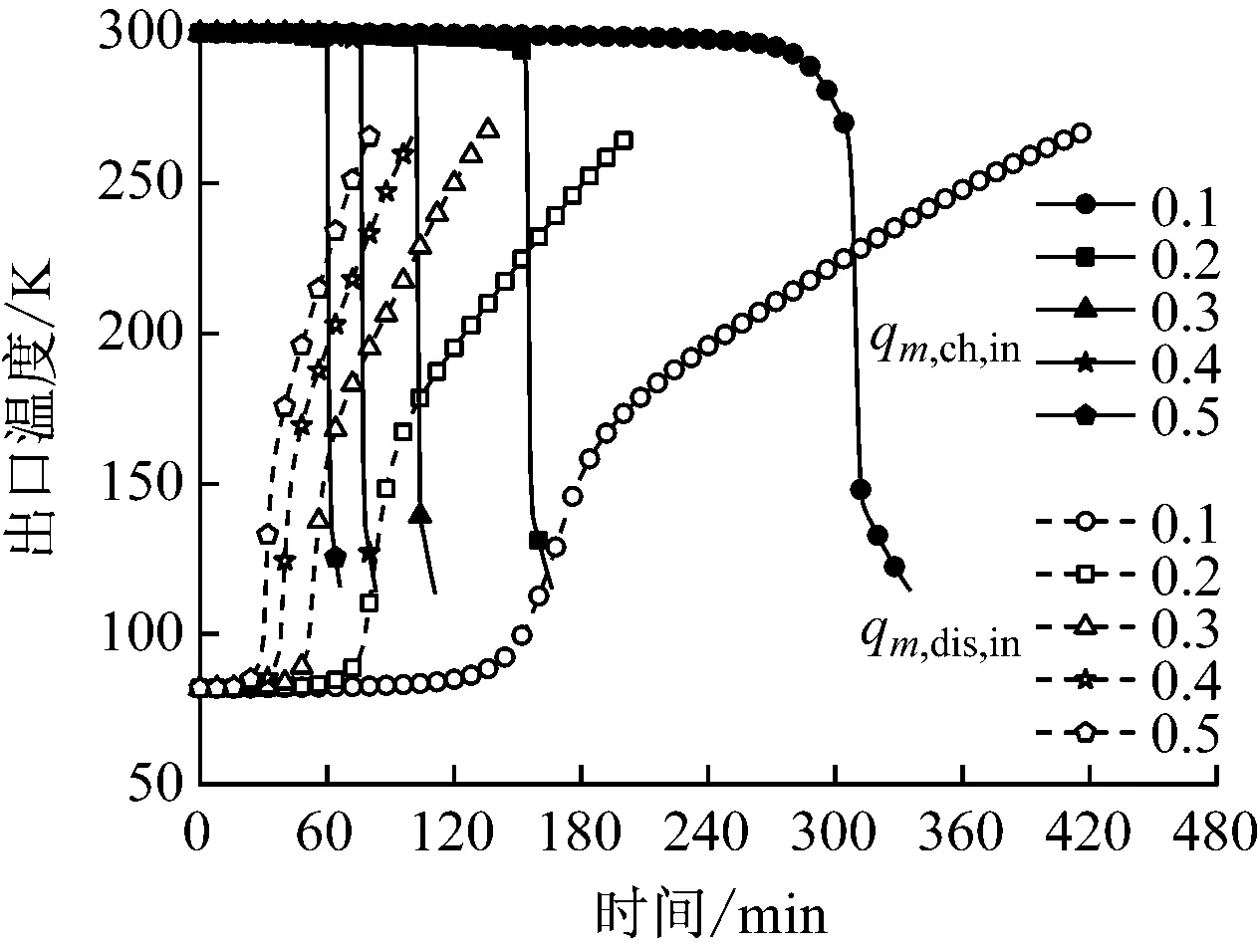
(a) 储释冷过程中蓄冷罐出口空气温度变化
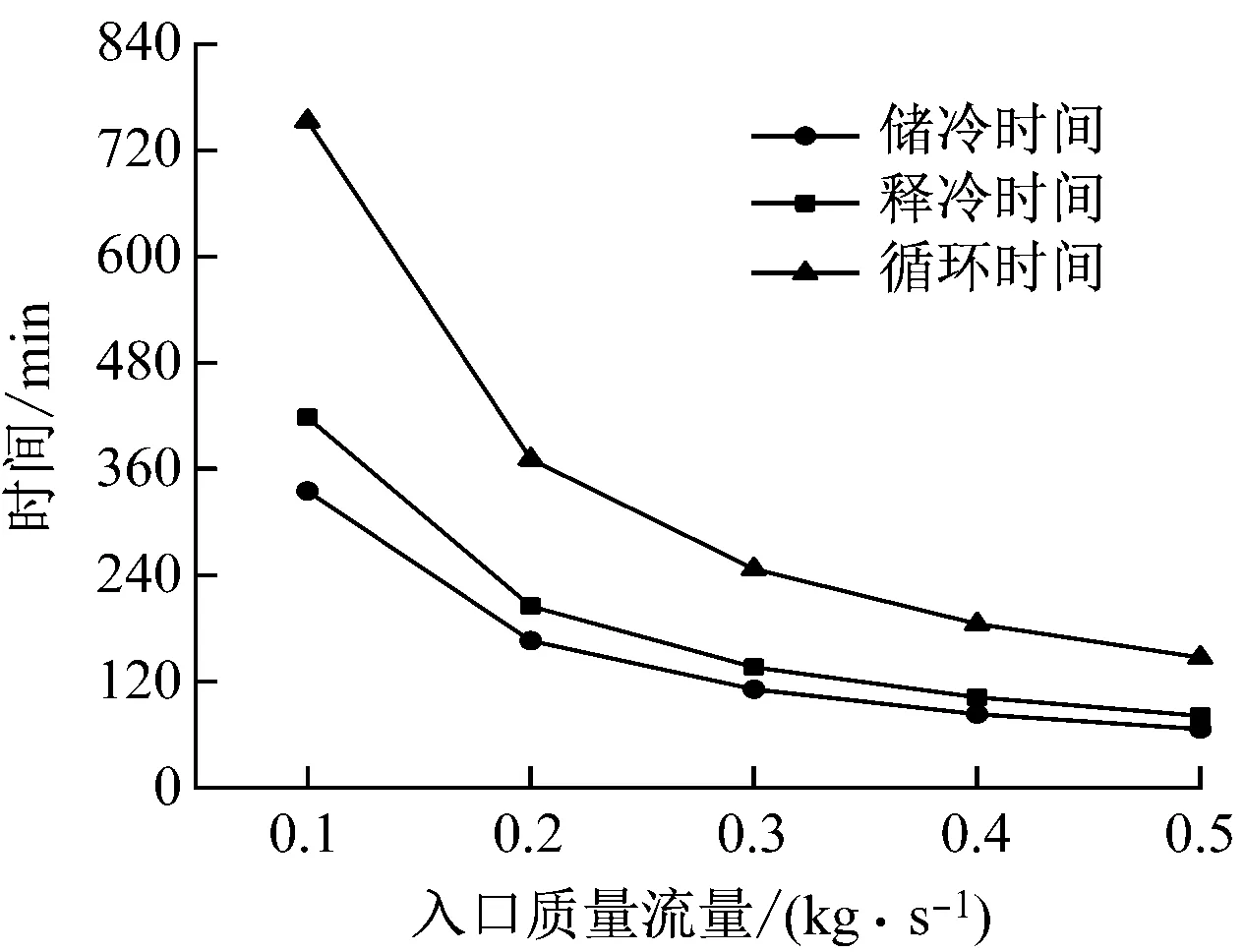
(b) 储释冷时间和循环时间图7 不同储释冷质量流量时可重复循环状态下各性能参数的变化(1)
图8给出了可重复循环状态下储释冷截止时刻蓄冷罐轴向温度分布和有效容量比。由图8(a)可以看出,储释冷截止时刻蓄冷罐轴向温度分布受储释冷质量流量的影响很小。当储释冷质量流量从0.1 kg/s增大到0.5 kg/s时,储释冷截止时刻蓄冷罐出口处温度的轻微变化使得有效容量比由93.7%先上升到94.8%,而后下降到94.4%。
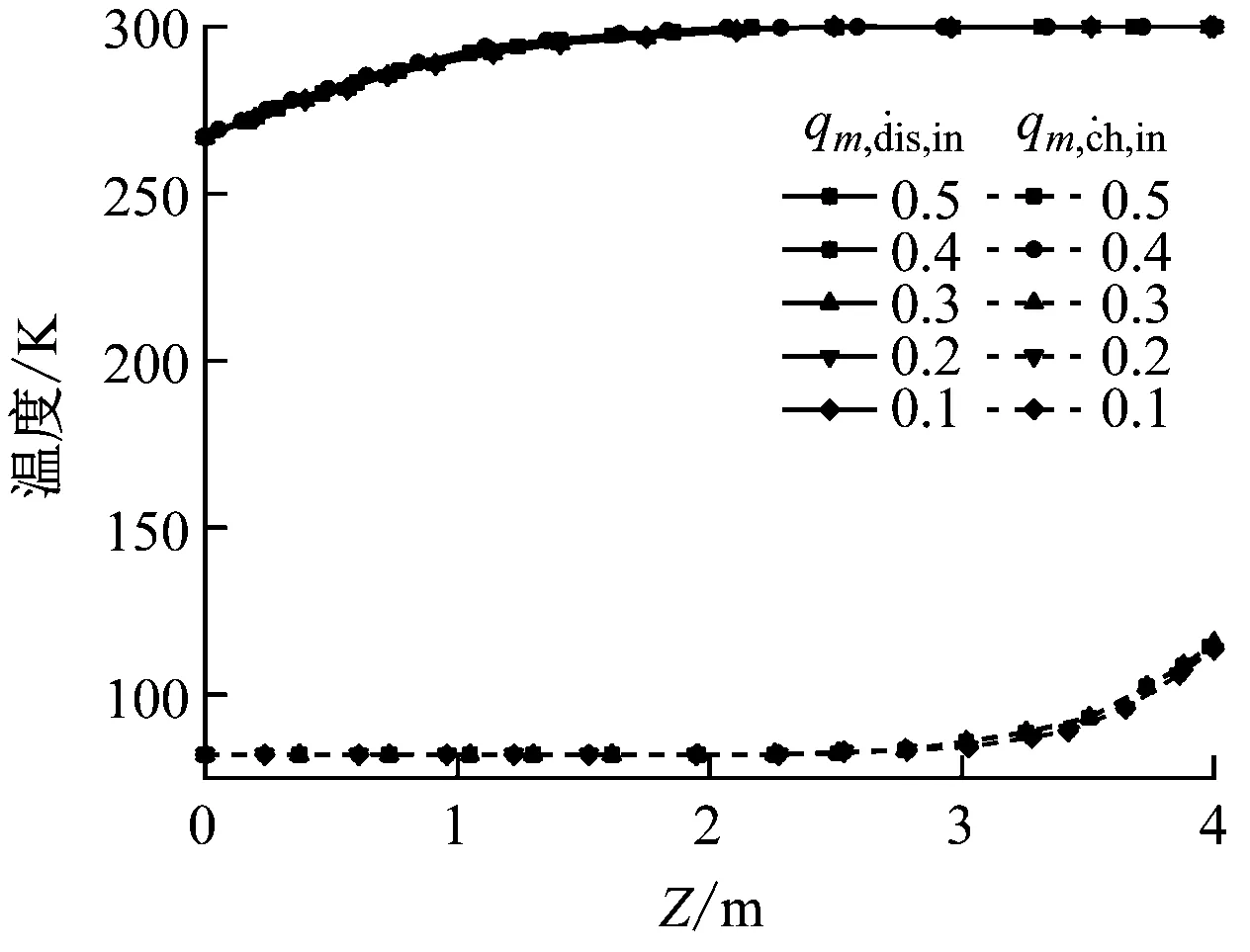
(a) 储释冷截止时刻蓄冷罐轴向温度分布
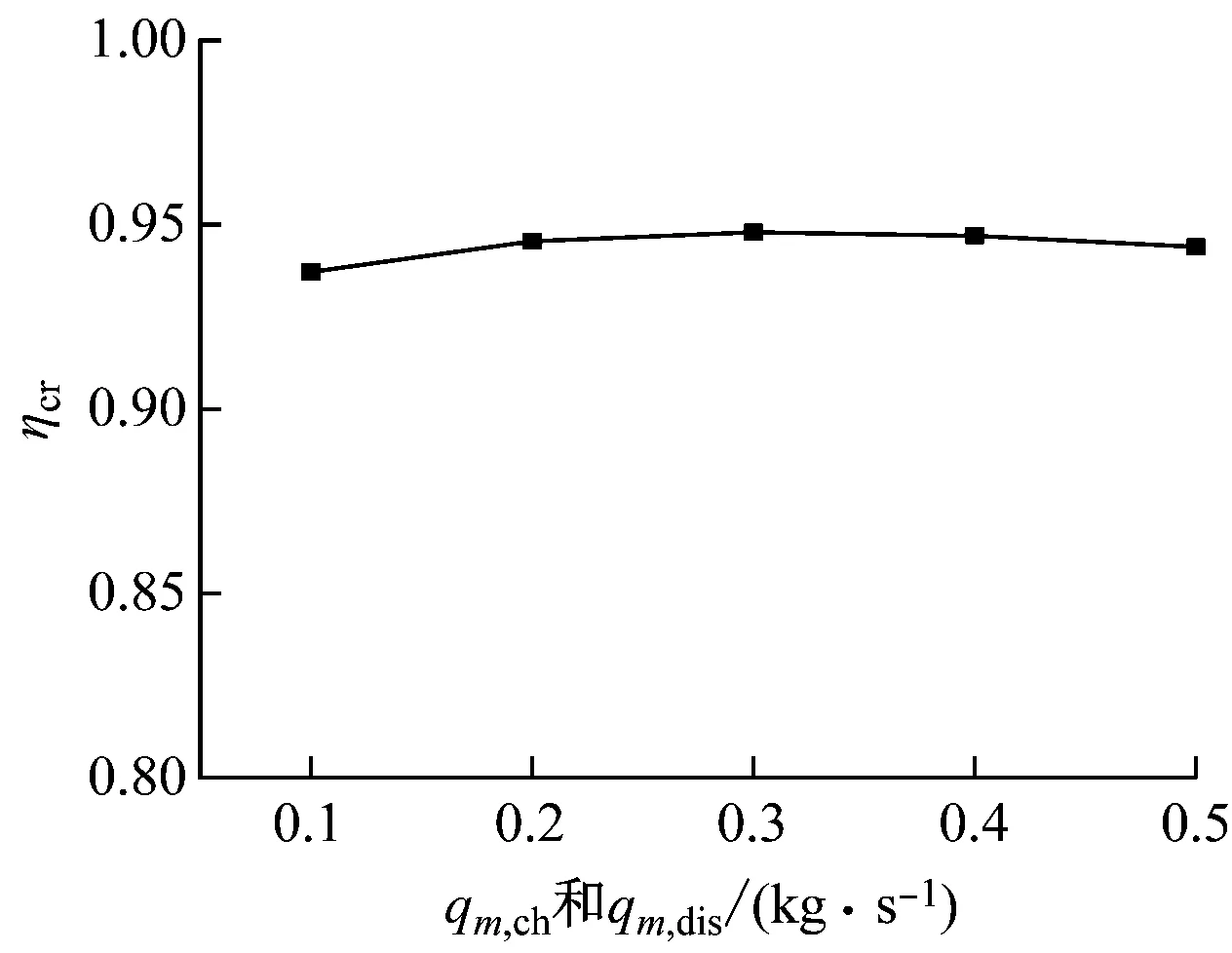
(b) 有效容量比ηcr图8 不同储释冷质量流量时可重复循环状态下各性能参数的变化(2)
2.4 蓄冷罐工作压力的影响
本小节分析储释冷过程中蓄冷罐工作压力对蓄冷罐循环性能的影响。对5种不同的蓄冷罐工作压力(pdis/pch分别为4.0/4.0、 8.5/5.5、 13.0/7.0、 17.5/8.5和22.0/10.0)工况下的储释冷循环过程进行模拟。这5种不同工况的储释冷截断因子均为0.85, 储释冷质量流量均为0.3 kg/s。
图9给出了可重复循环状态下储释冷过程中蓄冷罐出口空气温度、储释冷时间和循环时间的变化。由图9可知,当储冷过程中蓄冷罐工作压力由4.0 MPa增大到10.0 MPa时,储冷过程蓄冷罐出口空气温度的变化趋势几乎一致,储冷时间则由108 min小幅上升到114 min。而在释冷过程中,当蓄冷罐工作压力由4.0 MPa增大到22.0 MPa时,蓄冷罐出口空气温度时间段由29 min延长到55 min,斜温层导致的蓄冷罐出口空气温度上升段则由133 min缩短到77 min。这是由于释冷过程中蓄冷罐工作压力的上升使得斜温层变薄。由图9(b)可知,提高蓄冷罐工作压力有助于缩短循环时间。但是当蓄冷罐工作压力分别高于7.0 MPa和13.0 MPa时,再提高蓄冷罐工作压力,循环时间的缩短非常有限。
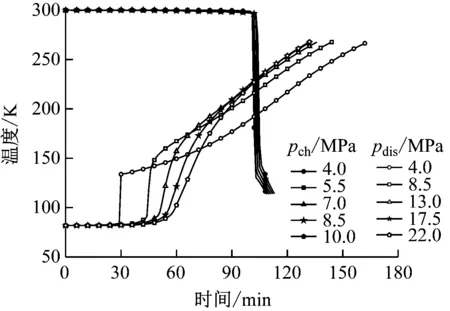
(a) 储释冷过程中蓄冷罐出口空气温度变化
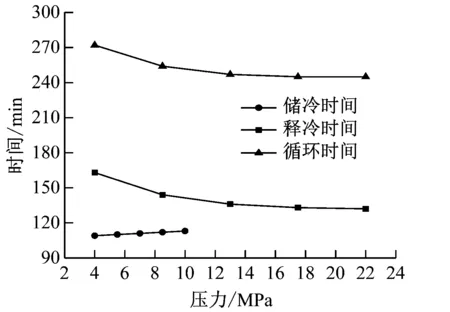
(b) 储释冷时间和循环时间图9 不同蓄冷罐工作压力时可重复循环状态下各性能参数的变化(1)
图10给出了不同蓄冷罐工作压力时可重复循环状态下储释冷截止时刻蓄冷罐轴向温度的分布和有效容量比。由图10可知,提高蓄冷罐工作压力对储释冷截止时刻蓄冷罐轴向温度的影响很小,5种工况下储冷效率均为95.0%左右。这主要是因为存储在蓄冷罐岩石颗粒的冷量不随蓄冷罐工作压力的改变而发生改变。
3 结 论
(1) 随着储释冷过程截断因子的增大,储释冷过程中蓄冷罐出口空气温度的变化趋势非常接近,储释冷斜温层厚度减小,蓄冷罐储释冷时间和循环时间显著增加,有效容量比明显增大。但是当储释冷截断因子高于0.75时,蓄冷罐的有效容量比高于90%。
(2) 随着储释冷质量流量的增加,斜温层移动速度加快,蓄冷罐出口空气温度出现陡增或者骤降的时间明显缩短,储释冷时间及循环时间迅速减小,但其减小的幅度逐渐变小,蓄冷罐的有效容量比变化较小。
(3) 储释冷循环过程中蓄冷罐工作压力的上升对储冷过程的蓄冷罐出口空气温度变化影响较小,但是会明显缩短释冷时间;另一方面对释冷过程的出口空气温度具有显著影响,在缩短释冷时间的同时会延长低温出口段的时间。
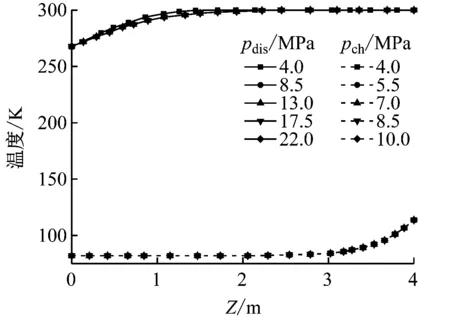
(a) 储释冷截止时刻蓄冷罐轴向温度分布
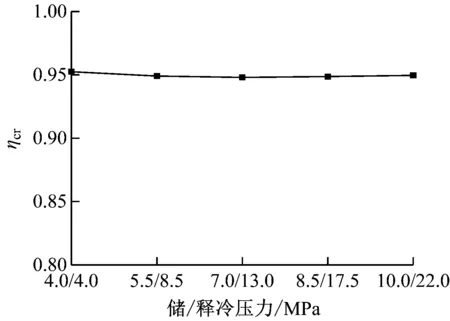
(b) 有效容量比ηcr图10 不同蓄冷罐工作压力时可重复循环状态下各性能参数的变化 (2)
