燃气轮机叶片热裂缺陷的应力形成及演化研究

2021-03-26杨啊涛李海松史卫杰王海洋张琼元杨照宏

动力工程学报 2021年3期

杨啊涛，郭雄，李海松，史卫杰，陶飞，王海洋，张琼元，杨照宏

(1.东方汽轮机有限公司，四川德阳 618000；2.长寿命高温材料国家重点实验室，四川德阳 618000)

铸造高温合金由于添加元素多、合金化程度高，因而具有良好的高温力学性能，在航空发动机和重型燃气轮机的透平叶片中有着广泛的应用，为了追求更高的热效率和功率输出，对透平叶片技术的要求越来越高[1-3]。高温合金叶片主要通过精密铸造方式成型，在制造和服役过程中如果出现裂纹、孔洞等各种缺陷，会导致叶片的机械性能达不到要求，容易发生断裂事故[4-5]。铸造高温合金力学性能优良，但铸造性能极差，再加上透平叶片结构复杂，使得叶片在精铸过程中常常出现缩松/缩孔、热裂和变形等严重缺陷。而热裂作为透平高温叶片的典型缺陷，其在众多缺陷中占比较大、报废率高、可修复性能差，严重制约叶片毛坯合格率。

根据现有文献，Feurer[6]根据热裂机理模型重点分析了凝固阶段转变点在热裂中的作用，指出当合金液补缩速度小于凝固收缩速度时，铸件发生热裂。Clyne等[7]提出热裂形成的主要原因是凝固后期热脆性区由于抵抗应力应变能力低，枝晶臂容易被拉裂。Rappaz等[8]提出了RDG判据，根据合金液的压力降来判断铸件是否产生热裂缺陷，当合金液压力降小于产生热裂的临界压力降时，铸件产生热裂，反之则不会形成热裂。Kool等[9-10]根据众多学者提出的热裂缺陷敏感性判据模型，模拟了铸造工艺因素对热裂缺陷产生的影响，并进行了实验对比。对叶片热裂缺陷形成机理的描述主要体现为以下2种观点：(1) 液膜理论，该理论认为，铸件在凝固末期晶间存在液膜和铸件在凝固过程中受拉应力共同导致热裂的形成，液膜是产生热裂的先决条件，而铸件收缩受阻是产生热裂的必要条件；(2) 强度理论，该理论认为铸件在凝固后期由于收缩受阻会产生拉应力及变形行为，当应力或变形超过合金在该温度下的强度极限或变形能力时，铸件便产生热裂。从研究结论可以看出，高温合金的力学状态是热裂形成的必要条件，因此，研究燃气轮机叶片的应力形成及演化过程对揭示热裂缺陷的形成机理是十分必要的。目前，针对热裂应力状态的研究文献较少，多数研究还是集中在工艺参数对热裂的影响，仅从侧面阐述了应力对热裂的影响行为。

笔者以某重型燃气轮机透平导向叶片为研究对象，采用数值模拟软件Procast分析了叶片铸造凝固区间的力学状态，阐述了热裂缺陷与应力演化的关系，并提出若干应力控制措施，消除了热裂缺陷。

1 实验及计算方法

1.1 叶片及浇注系统结构

选用某空心导向叶片作为研究对象，此叶片为二联体结构，叶片内腔依靠直立结构的陶瓷型芯成型。叶片最大长度约为250 mm，叶身壁厚约为3 mm。叶片上下缘板均有2处挂钩，挂钩的厚度约为15 mm，多挂钩的存在增加了叶片精铸的独立热节，增加了精铸过程中缩松/缩孔的风险。为消除此缺陷，浇注系统结构设计如图1所示。从图1可以看出，此浇注系统呈现框架结构，其结构间的约束较强，采用的组树方式为一带二。

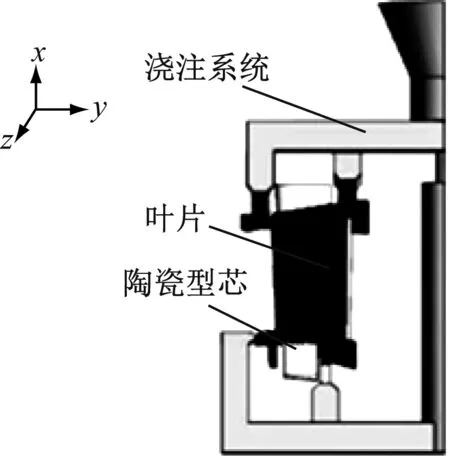
图1 透平叶片及浇注系统结构Fig.1 Structure of turbine blade and gating system

1.2 实验方法

采用熔模精密铸造工艺成型该叶片，合金选用MAR-M-247镍基高温合金，其名义成分(以下括号内的数值为质量分数)为：Cr(8.2%)、Co(9.2%)、Mo(0.5%)、W(9.4%)、Al(5.6%)、Ta(3.2%)、Ti(0.7%)、C(0.08%)、Hf(1.1%)、Ni(余量)。陶瓷型芯选用Si基耐火材料烧结成型。叶片浇注完成并经热处理后，进行X射线、表面荧光渗透检查(FPT)等无损探伤检测。同时，对FPT缺陷显示部位进行解剖处理，制成试样后在光学显微镜下观测缺陷的宏观和微观形貌。其中浇注温度为1 450 ℃，型壳预热温度为1 000 ℃，型壳材料选用EC95耐火材料，型壳层数为10层。

1.3 数值计算方法

1.3.1 温度场数学模型

其热传导过程遵循傅里叶定律：

(1)

热传导平衡微分方程遵循能量守恒方程(式(2)),据此可求解温度场。

(2)

式中：q为沿x方向传递的热流密度，W/m2；c为比热容，kJ/(kg·K)；ρ为流体密度，kg/m3；λ为热导率，W/(m·K)；T为温度，K；Q为合金的凝固潜热，kJ/kg；t为时间，s。

1.3.2 应力场数学模型

热裂缺陷主要在糊状区产生，因此仅分析糊状区的应力演化。因此，高温合金、型壳/型芯采用弹性材料本构模型，遵循胡克定律：

σ=Eε

(3)

式中：σ为正向应力，MPa；E为弹性模量，MPa；ε为正向应变，无量纲。

铸件在凝固过程中会因温差而形成热应力，因此含热应变的总应变表达式为：

(4)

式中：μ为泊松比；α为线膨胀系数，K-1；ΔT为温差，K；τ为切向应力，MPa。

式(4)为应力计算的物理方程，计算应力场时还需用到应力平衡微分方程：

(5)

式中：f为体力，N/m3。

1.3.3 铸造过程多场耦合计算及参数设置

铸造软件Procast在耦合计算温度场-应力场时主要是采取顺序耦合，即计算完温度场，将温度场计算结果作为载荷输入以计算应力场。对叶片及浇注系统进行网格划分，体单元数约为80万。计算采用的材料物性参数见表1。温度场计算边界传热系数为5 W/(m2·K)。

表1 材料物性参数

2 结果及分析

2.1 实验结果

图2(a)为叶片热裂位置示意图。经统计发现，热裂主要分布在图中A、B、C、D4个R角位置，其中B位置出现的热裂概率最高。图2(b)显示了D位置热裂宏观形貌，可以看出该热裂弯扭无序，且热裂宽度较大，有明显氧化色。通过测量热裂尺寸及位置可知，热裂距离上缘板汽道面约8 mm，热裂长度约为20 mm，深度约为3 mm，位于铸件表面。

(a) 热裂分布位置示意图

对叶片热裂缺陷区域进行解剖，并制备试样，置于光学显微镜下观察其微观形貌，结果见图2(c)。从图2(c)可以看出，热裂表面存在明显的贫化层，说明热裂在高温状态下形成；热裂沿途的枝晶呈裸露不连续状态，说明热裂形成于糊状区，同时在热裂附近发现大量共晶组织。

2.2 数值计算可靠性验证

为验证应力场数值计算结果的有效性，采用ATOS蓝光检测设备对浇注前后的铸件模型进行最佳拟合对齐检测，得出铸件的尺寸变化结果，其数值计算及实测结果见图3。

从图3可以看出，无论是叶盆还是叶背以及缘板部位，数值计算及实测得到的变形趋势及量级一致，说明应力、位移数值计算结果具有较高的可靠性，可用于后续的应力场计算及分析。

(a) 数值计算结果在最佳拟合下的尺寸变化

(b) 实测结果在最佳拟合下的尺寸变化图3 应力和位移数值计算与实测结果的对比Fig.3 Comparison of stress and displacementcalculation and experimental results

2.3 叶片凝固过程的应力计算

图4给出了叶片R角A、B、C、D点的应力状态。从图4可以看出，R角各点的应力值在固相质量分数0～1内始终保持正值，说明该R角处在糊状区，呈现持续拉应力状态，且各点拉应力不断增大，并在固相质量分数为1时最大，约为25 MPa。从图4还可以看出，应力增幅较大区间主要集中于固相质量分数0.8～1，说明凝固末期应力增速较快，此时可以推测，若固相质量分数在0.8～1的持续时间较长，累积的拉应力就越大，即凝固区间越大，凝固末期的拉应力也越大。另外，A、B、C、D点在凝固末期的应力极为接近，处于同一量级，表明各点具备同等热裂倾向。

图4 R角位置的应力Fig.4 Stress at R-angle corner position

为了更清晰地描述叶片铸件应力特点，笔者对叶片不同部位的若干点的应力行为进行了分析。所选取的点如图5(a)所示，其中1、2、3点分别为内浇道上表面点，而1′、2′、3′点分别为内浇道壁厚中心点，4点为叶盆面表面点，5点为下缘板挂钩表面点。

从图5(b)可以看出，1点在约200 s时出现拉应力最大值，约为12 MPa，随后应力不断下降，呈现压应力状态。4点相对于1、2、3点在相同的时间内应力增幅最大，说明1、2、3点的凝固速率相近，4点凝固较快，且早早进入固态冷却阶段，这也与温度场计算结果相吻合。图5(c)给出了1、2、3、4点应力与固相质量分数的关系。从图5(c)可以看出，在凝固末期固相质量分数为1时，4点呈现拉应力状态，其应力约为20 MPa；2、3点呈现拉应力状态，其应力约为8 MPa；而1点则呈现压应力状态，其应力约为-3 MPa。图5(d)给出了各点应力与固相质量分数的关系。从图5(d)可以看出，2′点的应力约为0 MPa，3′点的应力约为-5 MPa，而1′点在凝固末期固相质量分数为1时的拉应力约为25 MPa，与前文R角A、B、C、D点的应力相近，但此处并未出现热裂(内裂纹)，因此说明热裂的形成不仅需要满足应力条件，还可能需要其他条件，如凝固状态等。

(a) 点位置

(d) 各点的应力对比

2.4 无型壳作用的应力计算

由于上述计算考虑了实际型壳或型芯对铸件的阻碍作用以及应力。在分析应力形成及演化时，无法区分何种影响因素更大，因此需要计算应力分布。在Procast计算时，对型壳热物性参数正常赋值，对其力学性能参数赋值void，计算结果见图6。

从图6可以看出，B点在凝固区间拉应力最大值不超过10 MPa，而在型壳阻碍作用下，其拉应力最大值约为25 MPa(见图4)，说明型壳对R角处的铸件有绝对的阻碍作用。同理，4点在有、无型壳作用下的拉应力分别约为10 MPa和20 MPa，从图4和图6可以看出，有、无型壳作用时，位置点的应力会有明显区别。从结构上看，R角位置及4点位置具有界面突变或曲率较大的特点，这类结构特点下型壳在热胀冷缩时极易与铸件直接接触，严重制约铸件的收缩。而1、2、3点的应力呈现先拉应力后压应力的状态，与受型壳作用下的应力状态完全不同，这主要是因为铸件在凝固收缩时，与之匹配的型壳由于受热而膨胀，当其与铸件收缩方向一致，且在其他位置型壳的牵制下发生较大的位移，此时对铸件的作用就会体现为压应力。除此之外，1′点在有、无型壳作用下的应力分别为25 MPa和40 MPa，说明了型壳在不同铸件结构下扮演了截然不同的角色，或阻碍铸件收缩，或促进铸件收缩。

(a)

2.5 叶片凝固过程的应力形成及演化

众所周知，铸件由于结构间冷却速率不同而导致收缩量不同，从而引起热应力。选取1、5两相邻点分析凝固区间应力的形成与演化。首先，定义2类温度点分别为Tc(Tc=1 340 ℃，此时对应的固相质量分数为0.7)和Ts，其物理意义分别为开始线收缩的温度和固相线温度，温度高于Tc的区域由于液相较多，体现为液相体积收缩，无应力形成。图7给出了叶片不同点及型壳的温度曲线。

由图7(a)可知，当1点冷却至Tc时，应力开始形成，此时5点已冷却至1 198 ℃。当1点冷却至Ts(1 190 ℃)时，5点已冷却至996 ℃。在此阶段，1点的温降为150 K，5点的温降为202 K，即5点的收缩量更大，由于1点与5点处于相邻位置，两点距离构件的边界具备相同长度，因此此时间段内5点受拉应力，1点受压应力。同时，由于1点与5点为同一材料，具备相同的线膨胀系数，因此1点和5点的应力大小与两点的温降差(52 K)有关。

由图7(a)还可知，当5点冷却至Tc时，开始线收缩，此时1点的温度约为1 380 ℃，尚未开始线收缩，因此1点与5点之间收缩不受阻，不产生应力。当5点继续冷却至1 198 ℃时，1点的温度达到1 340 ℃，开始线收缩，此时1点与5点之间开始产生应力。当5点继续冷却至Ts时，5点凝固结束，此时1点的温度约为1 339 ℃。在此阶段，5点的温降为8 K，1点的温降为1 K。因此，此时间段内5点受拉应力，1点受压应力，1点和5点的应力大小与两点的温降差(7 K)有关。

计算B点型壳阻碍下的应力可知，在凝固阶段，B点的温降为150 K，而型壳的温升为40 K，此位置型壳的膨胀与铸件的收缩方向完全相反，说明型壳的膨胀对B点的收缩起绝对阻碍作用。此时，B点的应力为：

σ(t)=E(|α1(Tc-Ts)|+|α2ΔTB|)

(6)

式中：α1、α2分别为铸件、型壳的线膨胀系数，K-1；ΔTB为型壳在B点凝固阶段的温升或温降，K。

型壳对铸件的作用应视具体情况而定，取决于型壳对铸件的收缩是起拉伸还是压缩作用，这也很好地解释了前文B点与1、2、3点出现截然不同的应力结果的原因。

由以上分析可知，铸件区间的应力大小与温降差有关，要视平均冷却速率而定。对于有些特殊情况，起始冷却较快的构件可能随着凝固的进行，其冷却速率大幅度变缓，甚至小于起始冷却较慢的构件。此时所述构件间的温降累积差值较小，造成应力状态反转，即起始冷却快的构件最终反而形成压应力，起始冷却慢的构件最终反而形成拉应力；型壳对叶片应力的影响主要体现在型壳的位移大小与铸件收缩量是否一致。

2.6 工艺优化及验证

热裂的形成区域具有拉应力大的特点，但拉应力大的区域不一定会导致热裂，这说明应力对于热裂的形成来说是必要条件。从应力的控制角度出发，可以通过减小R角处的拉应力来减小此处的热裂倾向。根据应力的形成及演化，可以设计以下2种方案并进行浇注验证。

图8给出了2种应力控制措施示意图，分别为减薄R角型壳及增大叶片R角半径。经实验验证，2种控制措施均消除了热裂缺陷。减小R角处型壳厚度后，型壳的退让性大大提高，减小了对叶片收缩的阻碍作用；增大R角半径后，既减小了型壳对叶片收缩的阻碍和应力集中，又降低了R角位置的温度梯度，有效减小了叶片因温降差导致的应力。此外，还可以根据应力形成原理提出若干解决措施，如提高型壳预热温度以增加型壳退让性以及减小膨胀量等，合理优化浇注系统以控制叶片应力及型壳位移方向等。