基于数值流形法的反倾层状岩质边坡倾倒破坏模拟

王欢欢， 郭明珠

(北京工业大学城建学部， 北京 100124)

0 引言

反倾岩质边坡是指边坡坡面走向与岩层的倾向相反的边坡[1]。目前，国内外学者对反倾层状岩体的变形特征、破坏形式、成因机制、稳定性分析等方面做了大量研究[2-8]。Goodman和Bray等首先把极限平衡原理用于反倾岩质边坡的稳定性评价中[9]。安明旭等根据反倾岩质边坡弯曲破坏的特点，使用弯曲剪切-滑移破坏模式的分析方法，通过工程实例论证得出岩层倾角越陡、坡角越大，边坡的稳定性越差[10]。张志飞等基于颗粒流程序对反倾岩质边坡变形破坏过程进行模拟，结果表明岩层倾角对边坡整体性失稳破坏有较大影响，随着岩层倾角的增大，边坡后期整体性破坏方式由滑移型逐渐过渡为倾倒型破坏[11]。何怡等利用三维离散元软件3DEC模拟了边坡的倾倒破坏，通过多个算例对比分析发现，岩层倾角、底滑面倾角一定且剪出口高度与岩层厚度比值增大时，边坡产生倾倒破坏与倾倒-滑移破坏的可能性比较大[12]。程东幸等以龙滩水电站工程实例并结合三维离散元3DEC分析在人工进行边坡开挖的情况下，边坡坡角和岩层倾角对层状反倾边坡破坏的影响得出结论，边坡与岩层走向夹角20°左右是边坡发生倾倒变形的分界线[13-14]。左保成[15]、邹丽芳[16]等开展了反倾边坡的力学机理研究并进行了模型试验，分析了反倾边坡的破坏方式及其影响因素。黄润秋对倾倒滑坡进行工程地质分析，发现反倾岩质边坡发生倾倒破坏的斜坡坡角约为30°，其起始破坏的岩层倾角约为45°，对于大规模的深层倾倒来讲，最有利的岩层倾角为50°～70°[17]。骆波采用不连续体理论，利用离散元软件UDEC，在仅考虑自重作用下，建立了软硬互层边坡倾倒变形的因素和成因机制[18]。张沫利用FLAC3D建立反倾模型研究了地震波作用下的反倾边坡的高度、坡角、岩层倾角等对边坡破坏的影响，得出结论反倾斜坡高度越大，坡角越大，岩层倾角越小，反倾斜坡在坡内平行坡表的一定范围内越容易发生变形，甚至破坏[19]。

针对反倾岩质边坡的已有研究大多是以反倾岩质边坡的失稳模式和力学机理为主，采用数值流形法研究反倾岩质边坡不同岩层倾角倾倒破坏的较少。基于此，本文采用数值流形法来建立反倾边坡模型，对反倾岩质边坡岩层倾角的破坏过程进行数值模拟。

1 滑坡概况

贡扎滑坡位于西藏昌都地区芒康县索多西乡贡扎村，是岩质反倾滑坡，其前缘临江，受堆积体前缘阻隔，金沙江在此形成绕堆积体前缘的弧形河道，后缘及两侧均以干沟与山体相隔离，在地形上似圈椅状(图 1)，堆积体轴线走向NE51°，地面高程2384～2646im，总长约1013im，从地形地貌及空间分布特征看，堆积体表面地形平缓，坡度一般为5°～20°，前缘直达江边，与河床覆盖层直接相接。堆积体地貌总体形态如图 2所示。

2 数值流形方法

2.1 基本原理

数值流形方法是石根华博士于1991年提出的一种新的数值方法，其基本原理：“流形”来源于拓扑流形和微分流形，是指把许多个别的重叠的区域连接在一起，去覆盖全部材料体，由此得到的总体位移函数可以用局部覆盖的位移函数来进行计算。该方法使用两套网格(数学网格和物理网格)和两套独立的覆盖(数学覆盖和物理覆盖)，其中数学覆盖是用来定义近似解的精度并且由用户确定，物理覆盖系统是由数学覆盖和物理网格两者组成。物理网格包括材料体的裂缝、边界、块体以及不同材料区域的交界面，是用来定义其积分解的区域，每个物理覆盖都有独立的覆盖位移函数； 其中两个或两个以上的物理覆盖相交的公共区域称之为流形单元，每个单元上的局部位移函数可连接形成整个材料体上的总体位移函数[20]。该方法吸取了连续性和非连续性方法的优点，以数值流形为核心，在非连续变形方法(DDA)的块体系统非连续运动学理论的基础上，融入了有限元和解析法的连续分析方法，因此该方法既可以像有限元一样计算块体的内部变形，也可以像非连续变形方法一样模拟块体系统的力学行为。

2.2 覆盖位移函数和权函数

在数值流形法中数学网格和物理网格可以是任意多边形，因此应力的计算不能采用有限元中的等参单元法和高斯积分法，应采用多项式或解析形函数。形函数是在数学网格的时候定义的，具体形式是：

(1)

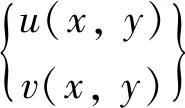
2.3 块体之间的接触处理

数值流形法中规定在每一时间步开始的时候算接触，每一个接触是由两条边形成的。每一对可能接触的边，在其时间步结束的时候，一条边对另一条边的嵌入或是进入均定义为接触。然后在实际的接触中是不允许两条边有嵌入的，所以接触的情况就仅是进入这一种。

该方法规定的接触可以分为角对角和角对边，其中边对边的接触转换为角对边的接触。其中两种接触有不同的参数和不同的刚性弹簧，相同的接触在不同的接触情况下也有不同的接触参数，其法向刚度设置如图 3所示。

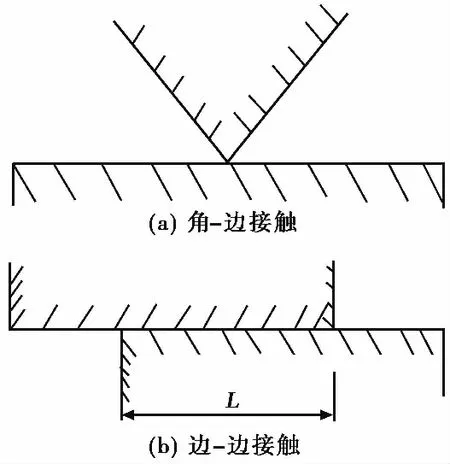
图 3 接触的模拟Fig.3 Simulation of the contact

角-角接触、角-边接触：

PN=k1E

(2)

边-边接触：

(3)

式中，P为接触刚度；E为接触块体的弹性模量；L是边-边接触时的接触长度；K1、K2是接触刚度增强系数，取值为10～100。流形单元采取的接触是罚函数接触，在接触点处允许少量贯入。接触力按照式(4)计算：

(4)

式中，FN，FT分别为法向和切向的接触力；dn、dt为在接触点处的法向和切向的变形。对于点-边接触和因破坏而失去黏接强度和抗拉强度的边-边接触，法向接触力不能为拉，切向接触力不能大于滑动摩擦力。

边-边接触时的接触应力：

(5)

3 算例分析

3.1 计算模型与计算参数

在进行数值计算的过程中，输入的参数会直接影响到数值分析结果的正确性，因此本文参数均以贡扎滑坡的力学试验得到的参数为标准。假设该边坡的基岩是一个类三角形坡体，其高度为1200im，底边长为1600im。通过室内力学试验以及野外调查结果得出的岩石及结构面物理力学参数见表 1。观察各种条件下的模型倾倒破坏模式，其边坡主剖面及网格划分计算模型如图 4、图 5所示。

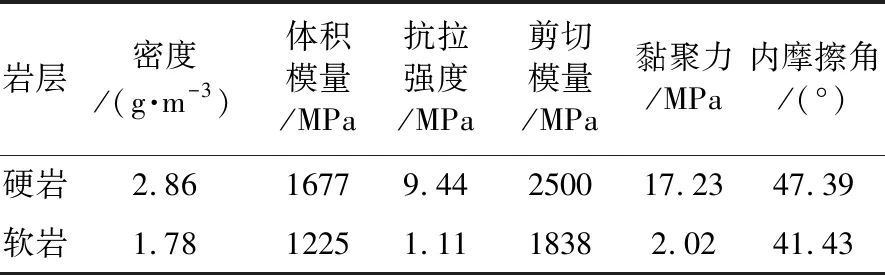
表 1 物理力学参数表Tab.1 Physical and mechanical parameters

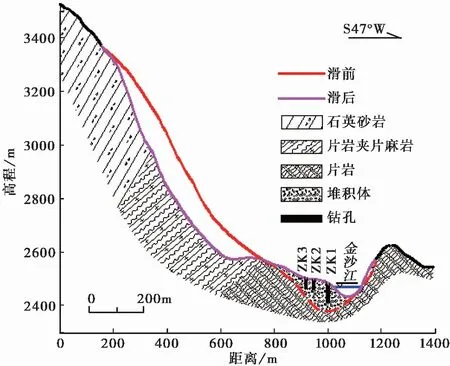
图 4 边坡主剖面图Fig.4 Main section of the slope

图 5 边坡网格划分模型图Fig.5 The model of slope mesh generation

3.2 影响因素分析

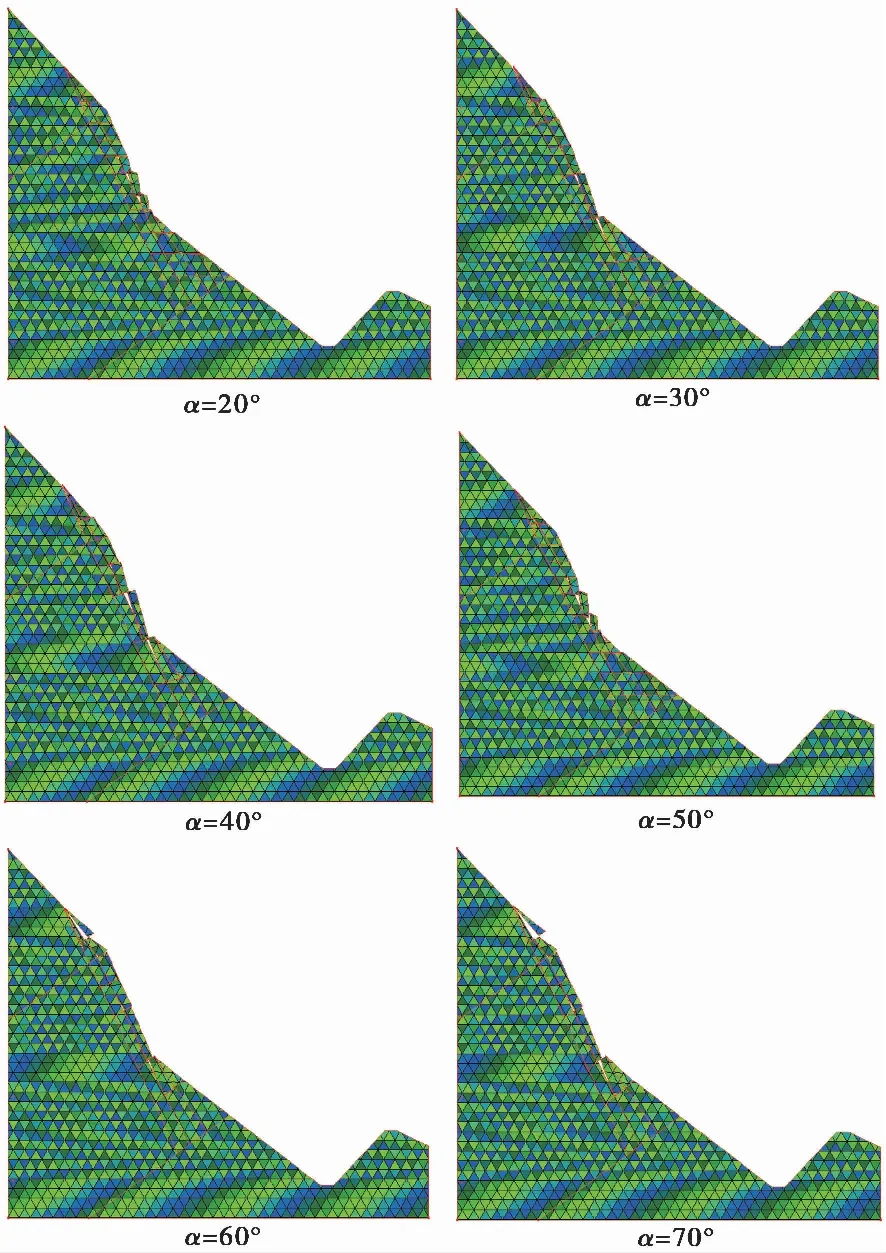
图 6 不同岩层倾角工况下岩石边坡的初始破坏状态Fig.6 Initial failure state of rock slope under different dip angles

模拟中只改变反倾斜坡的岩层倾角α，其他因素不变。通常倾倒滑坡体的岩层倾角在45°以上，主要集中在50°～80°。因此本文取岩层倾角α为20°、30°、40°、50°、60°、70°，模型的边坡坡角为40°，坡高约为1200im。对边坡各模型的倾倒变形模式进行分析。在本次数值模拟中，取计算总步数为2000步，时间步长为0.004s，最大位移比为0.0125，超松弛迭代系数为1.35，取岩石的弹性模量620iGPa，泊松比为0.25，密度软岩1.78×103ikg/m3，硬岩密度2.86×103ikg/m3，仅对边坡的倾角采取不同的值，对边坡的破坏过程进行模拟，岩石边坡的破坏过程如图 6所示。

不同岩层倾角下边坡初始破坏状态如图 6所示。模拟结果表明当岩层倾角小于45°时，反倾斜坡的变形破坏是从边坡中部倾倒区开始的，由于倾倒区的破坏使得上部的稳定区岩石逐级发生破坏成为了倾倒区的主体，从而提供了巨大的下滑力推动下部岩体发生滑移，进而使得整个斜坡发生倾倒破坏； 当岩层倾角大于45°时，变形是由边坡下部逐渐向上部坡顶发展，且边坡上部也会出现十分明显的弯曲变形，呈“点头哈腰”式变形破坏。

4 结论

本文的主要目的是利用数值流行方法来探讨重力作用下层状岩质边坡在不同岩层倾角下的破坏模式。研究结果表明：岩层倾角45°是边坡发生破坏的临界角度，当岩层倾角大于45°时，模拟显示边坡的变形是由边坡下部逐渐向上部坡顶发展，并且边坡上部也会出现十分明显的弯曲变形，呈“点头哈腰”式变形破坏。但是由于此次计算选择的模型较简单，因此与实际的边坡模型结果存在一定的差距。