考虑抢修时间的铁路应急物资配送与失效线路修复的集成优化

何珊珊

(防灾科技学院， 河北 三河 065201)

0 引言

2008年5月12日，四川汶川发生8.0级特大地震，宝成铁路109号隧道山体崩塌，导致正在穿越109号隧道的一列油料车脱线并起火，宝成铁路因此中断。灾害发生后，铁路部门迅速行动，组织抢险，经过12个日夜奋战，装载着救援物资的977次列车从该隧道通过，驶往四川地震灾区[1]。2018年9月12日，陕西省汉中市宁强县发生5.3级地震，兰渝铁路陇南至羊木区间震感明显，为确保行车安全，兰州局集团公司封锁了兰渝铁路部分线路，连夜排险抢修，科学指挥行车[2]。可见，铁路应急处置是确保铁路运输畅通的坚强后盾，对保障国民经济稳定发展有着重要意义。地震等自然灾害不仅威胁着铁路运行的安全，也改变了路网结构和性能，严重影响了铁路应急物资的配送效率[3]。因此，对于震后失效线路的抢修安排至关重要，同时还要考虑如何合理的协调失效线路抢修与应急物资的配送顺序，做到二者的集成优化[4]。

现阶段在应急物流动态网络规划的应用方面，多见关于应急物资配送路径的研究，较少考虑应急路网的损毁情况。施晓岚按照应急物流特性和规划任务，明确地将应急物流网络规划分为静态网络规划与动态网络规划，并指出动态网络规划对灾后救援的重要性[5]。在铁路应急物流网络规划方面，王璞等给出基于层次分析法和包络分析法的铁路应急资源需求紧急度评价方法[6]； 郑斌等利用双层规划方法研究了震后应急物流系统中的公铁多式联运问题，并设计相应的混合遗传算法[7]。在可变路网方面，李志等指出设施中断现象会影响整个物流系统的运行效率[8]； 周愉峰等考虑震后救援初期的阶段性特征、设施中断情景和设施能力限制等因素，建立了一个适用于震后救援初期的应急设施选址-分配模型[9]； 何珊珊等改进了dijkstra算法对路径问题进行优化，建立了机会约束规划模型以解决具有随机抢修时长的路径规划问题[10]； 孙世超建立了以行程时间为动态随机变量的随机时变网络模型[11]； 李耀南等基于路网修复所需资源和路段通行能力，构建了双层修复模型并设计了改进的粒子群优化算法求解，增加了扰动因子，克服传统算法在处理该问题时收敛速度慢且精度低的缺陷[12]。结合以上分析，发现这些研究在模型假设中都没有考虑失效线路的抢修时间，多数认为在优化后的抢修方案中，物资配送途经利好线路时，该利好线路就已经修复连通了，显然在应急物资缺乏的初期，此假设是不符合实际情况的，因为只有在时间窗内修复好该线路，才会改善整体路网情况。

目前，考虑失效线路抢修时间的铁路应急物流动态网络集成优化的研究不多，在抗灾救援活动中有必要根据失效线路的抢修时间这一关键因素，进行应急物资配送与失效线路修复的集成优化，达到应急物流动态网络的系统最优[10]。本文针对应急救援初期时间紧迫、资源有限和路网动态变化等特点，在铁路应急物资配送网络中，列车采用多安置点配送的运输方式，考虑在实际可变路网中的具有大规模物资需求，建立了集成优化模型，同步解决了带有时间因素的抢修失效线路与应急物资配送问题，并考虑了大规模应急物资需求随时间变化的动态性，提高了铁路应急物流调度的执行效率。

1 动态网络集成优化模型构建

图 1是某地震后铁路局域网络示意图，受灾害影响致使调度周期内路网中的某些线路失效而无法通行，随着主干线不断被修复，路网会显现随时间变化的状态，相对以往静态铁路网最优配送路线的方法，将不同抢修方案带来的动态路网情况引入铁路应急物流调度优化问题是值得进一步研究的，其本质就是在资源有限和路网动态变化的情况下，寻求应急救援效益最大化而主动选择利好的路网结构。

1.1 模型假设

为保证研究的合理性和有效性，首先对问题作如下假设：(1)应急救援初期，救援中心的供应物资小于需求量，可分别用于配送至安置点和投入修复失效线路； (2)有效线路在定义时间间隔内正常通行，失效线路的抢修完成时间可以事前预知； (3)在某个应急救援阶段，应急物资的实际需求量随时间的推移而变化，且变化率为定值； (4)各应急物资安置点对物资要求的最迟满足时间可知，可以理解为超过该时间节点会造成一定的生命财产损失； (5)列车从应急救援中心出发后，中途不再返回救援中心； (6)在安置点产生的装卸时间不计。

1.2 线路抢修时间窗约束

线路抢修时间是指在图 1中的动态路网中，失效线路p在抢修时间tp之前，对应边是不连通的，若该失效线路是利好线路，对于从该边一个顶点向另一个顶点行进的出发时刻必须要大于等于tp，也就是说必须等待到该边连通为止才可以出发。

下面用数学规划语言表达抢修时间窗约束，引入广义抢修时间变量Tp即：

(1)

式中，P为失效线路集合；yp为0-1变量，yp=0表示该失效线路不在利好路网中，因此不用抢修，此边不连通，可以认为Tp=+∞；yp=1表示该失效线路是利好线路，必须抢修至该边连通，抢修完成时间为预计时刻tp。

(2)

式中，K车次集合；xijk为0-1变量，xijk=1表示列车k从节点i到节点j，否则为0；Tik为列车k到达安置点i的时刻，若Tik≥Tp，则直接沿着该线路向另一个顶点j行进时配送，否则，必须在顶点i处停车等待至时刻Tp后出发。

从整个系统来讲，即使在利好线路顶点处停车等待，造成的损失也会比绕行的损失要小，这时到达顶点j的时刻表示为：

(3)

式中，A=J∪{o}，J为物资安置点集合，o为应急救援中心；tijk为配送列车k从节点i到节点j所需的行进时间。由于超过各应急物资安置点对物资要求的最迟满足时间会造成一定的生命财产损失，有必要考虑配送物资产生的延误时间，由以下约束条件确定：

Tok=0，∀k∈K

(4)

0≤Tjk-Δtjk≤dlj·zjk

(5)

Δtjk≤M·zjk，∀j∈J，k∈K

(6)

式中，zjk为0-1变量，若zjk=1，表示k车为安置点j配送，允许有延时Δtjk≤M(M为任意大的正数)且满足式(5)，若zjk=0，表示k车不为安置点j配送，延时Δtjk=0。dlj为安置点j应急物资的最迟满足时限。

1.3 集成建模

在满足失效线路抢修时间约束的前提下，对铁路应急物流动态网络进行集成优化，得到最佳的失效线路抢修方案、列车行车路线及各个应急物资安置点的配送量和延误成本，达到铁路物资运输效率最优。优化目标主要体现在如下表达式：

(7)

目标函数z中第一部分表示带有安置点的配送物资总延时，由于在应急配送过程中，延误的资源量越大，产生的时效性就越差，用此目标体现应急物资配送的时效性。Yj为安置点j的物资配送量：

(8)

式中，s为应急物资救援中心供应量；qj为安置点j的初始物资需求量；dp为抢修线路p所占用的应急物资量。式(8)表示安置点j由于应急物资匮乏同时抢修失效线路占用导致，并将其余物资按初始需求量加权分配的实际配送量。

目标函数第二部分表示安置点总的物资未满足量，η为两目标均衡系数。需要强调的是，这里考虑了物资未满足量随时间变化的动态性。为了符合应急救援初期的实际背景，随着时间的推移，物理环境的变化，受灾人数的上升使得物资需求量发生变化，由于配送的计划性，致使物资未满足量也会发生变化，同时为了简化数学模型，设物资需求变化率为α，采用如下形式的关于时刻t的需求量函数：

qj(t)=qj(1+α)t

(9)

则安置点j的实际未满足量可以表示为：

Uj(t)=qj(t)-Yj

(10)

其他配送约束如下：

(11)

(12)

(13)

(14)

(15)

ck为车次k的载重，式(11)表示列车的载重量约束，式(12)表示从救援中心派出的列车数不超过总列车数，式(13)表示每个安置点仅且只被执行一次，式(14)～式(15)表示决策变量之间的关系。

综上，考虑抢修时间因素的铁路应急物流动态网络规划的集成优化就是以式(7)为目标函数，以式(1)～式(6)，式(8)～式(15)为约束条件的集成优化数学模型。

2 模型求解

基于建立的集成优化模型属于NP-hard问题，本文采用改进的遗传算法对集成优化模型进行求解，设计自适应交叉概率和自适应变异概率来降低过早收敛的可能性，同时加快寻优速度，图 2为改进遗传算法流程图。

2.1 编码方案设计

本文遗传算法中的每个染色体包含抢修方案和行车配送路线两个方面，所以设计了为每条染色体有2个子串构成，子串1有︱p︱个基因位(︱p︱为失效线路数量)，采用二进制编码，随机产生︱p︱个0-1变量，每个基因位的取值为1代表抢修对应失效线路，反之不抢修； 子串2有︱J︱个基因位(︱J︱为应急物资安置点数量)，采用浮点数编码，随机产生︱J︱个介于(1，k+1)的互不相等的浮点数(保留两位小数)，浮点数的整数部分为车次编号，被同一列车服务的安置点所对应的浮点数整数部分相同，小数部分升序排列表示列车服务个安置点的顺序。

假定某问题中失效线路有3条，应急救援中心有3趟列车，有8个安置点需要应急物资，按照如下方式进行编码：

(1)随机产生3个0-1整数编码和8个介于(1， 4)之间的浮点数构成一个染色体：

0-1-1-1.42-3.25-3.76-2.73-2.43-1.89-3.57-2.21

后八位浮点数与安置点一一对应。

(2)将后八位浮点数按从小到大分组排序：(1.42， 1.89)、(2.21， 2.43， 2.73)、(3.25， 3.57， 3.76)。

(3)根据分组排序的结果可知，编码方案表示抢修失效线路2和3，列车行驶线路为：

车次1： 0-1-6； 车次2： 0-8-5-4； 车次3： 0-2-7-3。

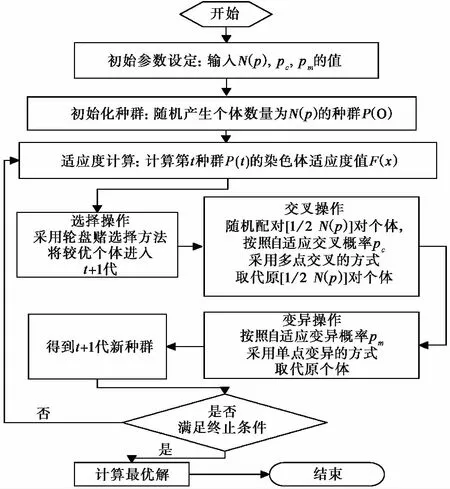
图 2 改进遗传算法流程图Fig.2 Flow chart of the improved genetic algorithm

2.2 设计自适应交叉和变异概率

(16)

(17)

3 算例分析

假设某地区突发地震灾害，附近7个救援安置点需要依靠铁路局域网从应急救援中心紧急调运物资，受地震灾害影响较大，安置点之间以及与应急救援中心之间部分线路失效，需要选择抢修利好线路，可缩短列车运行时间，但也要消耗有限的物资。

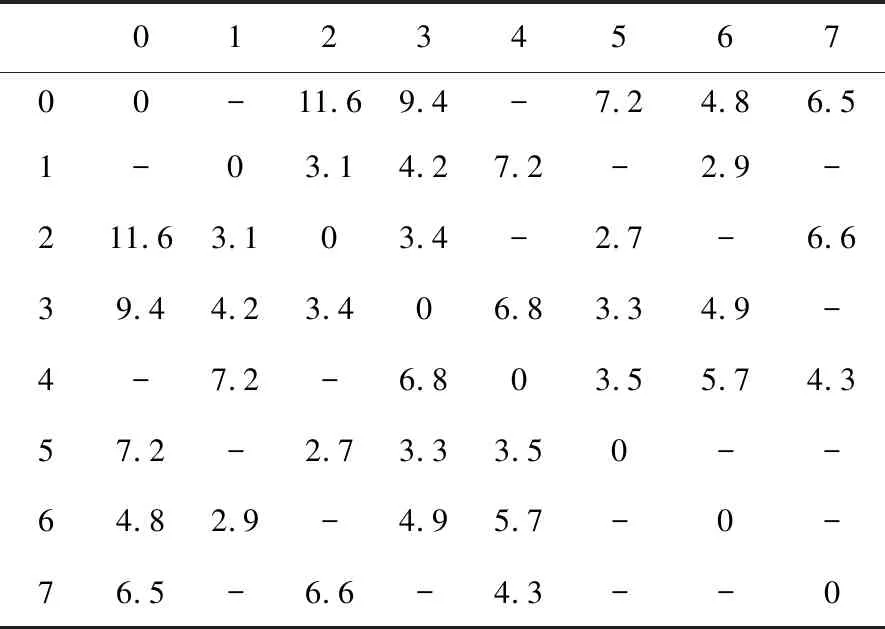
表 1 列车运行时间(h)Tab.1 Train operation time(h)

假设应急救援中心能供给的物资在调度之前已确定，数量有限，且中途无物资补给。根据1.1节假设条件，对有关数据作如下处理和说明：应急救援中心仓库供应救援物资190t； 列车2列，最大载重为90t，运行时速恒定，α取0.05，η取0.8，列车在应急救援中心点与7个安置点之间的运行时间如表 1所示。对失效线路进行编号，安置点1与安置点3之间的路段编号为线路A，安置点1与安置点6之间的路段为线路B，抢修线路A和线路B所需要的物资成本为10t，抢修完成时刻为10h。记应急救援开始时刻为0h，安置点物资需求量及最迟满足时限由MATLAB随机产生，见表 2。

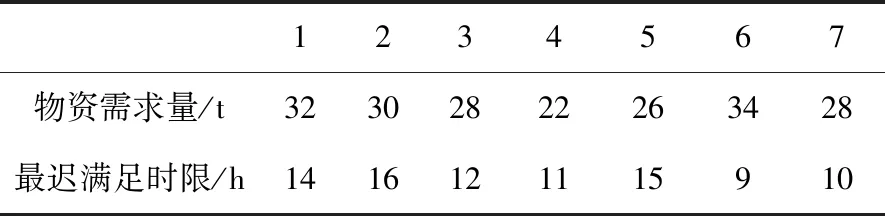
表 2 物资需求量及最迟满足时限Tab.2 Material demand and deadline

根据上述数据，采用改进遗传算法对模型进行求解。程序经多次调试，遗传算法控制参数设定如下：种群规模为200，最大迭代次数为1000，交叉概率λ1=0.7，λ2=0.9，变异概率λ3=0.005，λ4=0.01。

运行程序一次性求得最优目标函数值为56.8，列车行驶路线见表 3。算法收敛时间在116s，收敛速度较快，最佳抢修方案及列车运行线路如表 3所示，安置点实际物资未满足量及延时时长如表 4所示。

表 3 最佳抢修方案和最优线路Tab.3 Optimal repair route and optimal route

表 4 需求未满足量和时延成本Tab.4 Insufficient demand and delay cost

为体现所建数学模型的集成优化优势，现对四种确定路网结构分别逐一进行求解得到列车最优线路如表 5所示。

表 5 四种路网下的最优线路Tab.5 Optimal route under four kinds of railway network

对比发现，采用改进遗传算法求解的集成优化模型能一次性得出失效线路的最佳抢修方案和列车行驶线路，提高了可变铁路网下应急物流调度数学算法的执行效率。

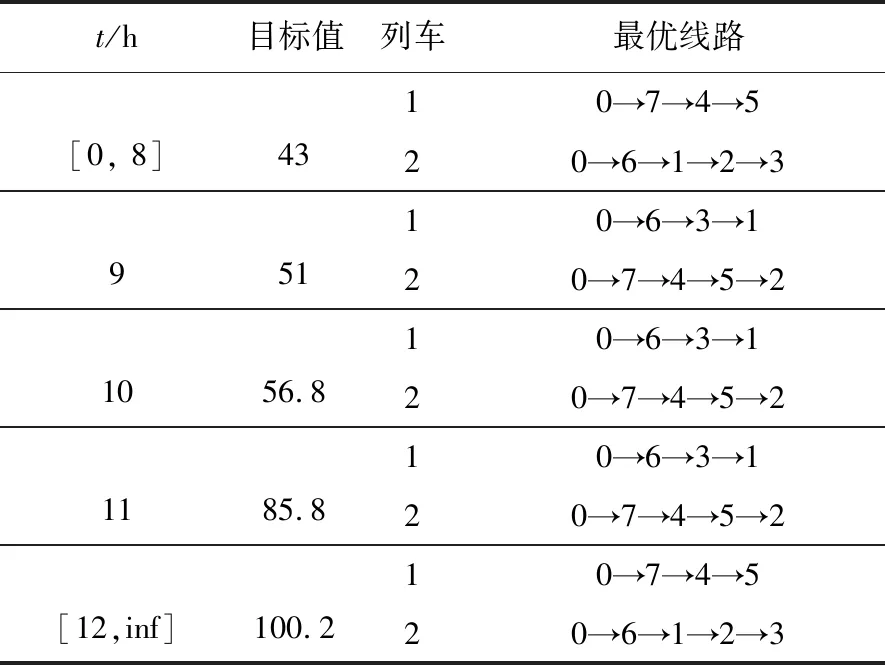
表 6 只抢修线路A时抢修时刻ta的灵敏性分析Tab.6 Sensitivity analysis of ta under repairing line A alone

由于抢修失效线路会占用一定的物资量，非利好线路可以不用抢修，所以全部线路抢修不一定会优于部分利好线路的抢修。

另外，抢修失效线路的完成时刻作为已知参数，其变化也会导致目标函数值和列车最优路线发生变化。在最佳路网结构即只抢修线路A的情况下，目标函数值及最优线路随失效线路抢修时刻参数ta变化的灵敏度分析如表 6所示。

算例结果表明，相对其它路网结构，最佳抢修方案的目标值随参数扰动相对稳定，仍然具有较大优势。

4 结论

针对震后应急物资配送过程中，铁路网络存在失效线路导致路网结构会发生动态变化的情况，对抢修失效线路的选择和列车的配送线路集成优化，模型从实际背景出发，主要考虑了失效线路的抢修时间，建立集成优化模型，并设计了基于改进遗传算法的一次性求解策略进行求解，通过算例分析验证了模型和算法的可行性及有效性，对铁路应急救援的作业调度人员制定列车行驶方案具有一定的指导意义。进一步的研究主要集中在抢修方案的复杂因素方面，将其作为下一步研究方向。