结构抗震设计中地震动参数选取的几个基本问题

郭 迅， 何 福， 周 洋

(防灾科技学院 中国地震局建筑物破坏机理与防御重点实验室，河北 三河 065201)

0 引言

我国现行建筑抗震设计规范确定的基本原则是“小震不坏，中震可修，大震不倒”[1]，具体操作时作为基本设防烈度的中震一般不直接表现出来； 并且同一烈度对应多个表征地震动强度的加速度值或系数，这样的做法给工程师带来理解上的困难，实践中不便操作。实际上，地震动参数的内涵非常丰富，包括设防烈度、超越概率、地震动持时、频谱特性、断层影响等，结构设计时不同的验算内容对应不同的选择。1989年之前，我国几个版本的抗震设计规范均采用确定性理论，只要场地的设防烈度确定，地震作用就随之确定，结构抗震性能的好坏用结构系数来体现。引入概率理论以后，表述地震作用的多个参数如何恰当地使用对许多工程师是一个挑战。本文利用几个具体案例阐明地震动参数选取的注意事项。

1 地震动参数选取现状

图 1 时程分析法7度小震地震动PGA为0.035gFig.1 The PGA is 0.035g for small earthquake event corresponding to intensity 7 in the time history analysis method

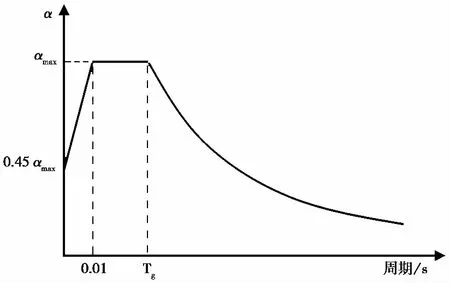
图 2 设计反应谱中地震影响系数与结构周期的关系Fig.2 Relationship between seismic influence coefficient and structural period in design response spectrum

以7度区(0.10g)为例来说明地震动强度的各参数的使用。对于7度区的结构，当采用时程反应分析方法求解结构构件强度验算所需的地震内力时，对应7度小震阶段，需要将选定的地震动时程的PGA(地震动峰值加速度)调整为0.035g(图 1)； 当采用反应谱方法求解构件强度验算所需的地震内力时，同样属于小震阶段，反应谱平台高度取值αmax=0.08(图 2)。进行结构抗倒塌验算时，应选取7度大震对应的参数，当采用时程反应分析法时，需要将选定的地震动时程的PGA调整为0.22g； 按照反应谱法求解地震内力或变形时，反应谱平台高度取值αmax=0.50。至此，描述7度地震动强度的参数已经有4个了。此外， 7度地震的中震对应的PGA为0.10g，这样描述7度(0.10g)地震的5个参数就齐全了。位于8度(0.20g)区的结构，描述地震动强度的5个参数几乎加倍(仅大震水平地震影响系数最大值由0.50增加为0.90)。同样道理，其他烈度由低到高，每提高1度，除大震水平地震影响系数最大值外，其他各参数量值加倍，上述各参数取值见表 1和表 2。

表 1 用于时程分析的地震加速度峰值(cm/s2)Tab.1 PGA for time-history analysis(cm/s2)

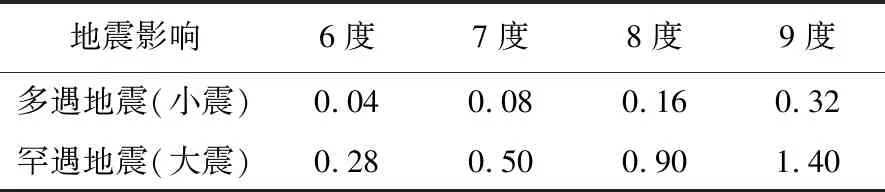
表 2 水平地震影响系数最大值Tab.2 Peak value of horizontal seismic influence coefficient

2 地震力取值的历史沿革

从上述实例可知，给定烈度以后地震动参数的选取是容易混淆的。我国早期的抗震设计规范(比如1964版[2]和1978版[3])非常简单。以地面加速度峰值来描述，规定7度对应0.10g， 8度对应0.20g，依此线性规律类推。自1989版抗震设计规范[4]开始采用概率理论，假定某一地区的地震动强度分布符合概率理论中的极值Ⅲ型分布，小震50年超越概率63.2%，中震50年超越概率10%，大震50年超越概率2%～3%(图 3)。中震对应设防烈度，也称基本烈度，与老规范的烈度相对应。每一地区的设防烈度由《中国地震动峰值加速度区划图》[5]确定。小震比中震低1.55度，其加速度取值约为中震的1/3； 大震比中震高1度，其加速度取值约为中震的2倍，这是依据概率理论对旧规范的继承和发展。此外，在计算地震剪力时用到的地震影响系数还涉及到结构地震放大效应，比如反应谱平台高度比出发点高出2.25倍(图 2)。超越概率与放大效应绞缠在一起，对地震力大小的理解造成困难。为便于理解，需要从源头梳理一下地震力发展的历史沿革。

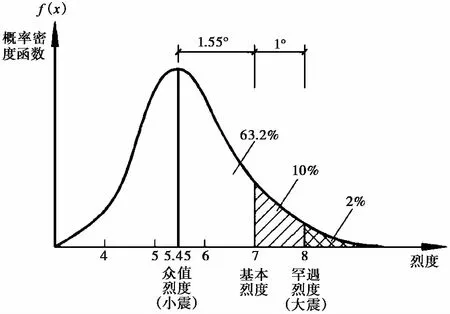
图 3 地震烈度概率密度分布示意图Fig.3 Distribution of probability density of seismic intensity

早期规范(我国1978版及之前)是不考虑概率问题的。1891年日本发生浓尾地震，明治维新以来用现代材料和结构形式建造的一批房屋遭受严重破坏。日本的大森房吉[6]基于对实际震害的思考，提出将地震效应视为作用于建筑物上的水平推力，大小相当于建筑物自重的十分之一，这是“刚性法”的最初萌芽。1906年美国旧金山大震发生后，日本的佐野利器[7]结合浓尾地震震害情况，得出多层房屋受到的水平地震荷载总量也是重力的十分之一，该研究同大森房吉一样，不考虑动力放大效应，地震作用相当于静水平力，所以称之为“静力法”。1933年美国长滩地震获得强震记录以后，Biot[8]及Housner[9]等提出并发展了反应谱的概念，把结构视为图 4所示的弹性体，在往复地震作用下，楼板相对地面有放大效应，平均放大倍数β约为2.5。

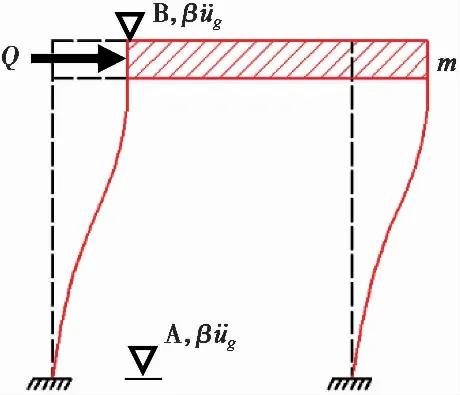
图 4 弹性结构对地震动的放大效应Fig.4 The amplifying effect of elastic structure on ground motion

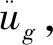
(1)

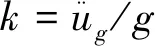
Q=βkmg=βkW=αW

(2)

其中，α=βk是无量纲的、考虑放大效应的地震影响系数；W为产生地震荷载的建筑物总重量，包括恒载和楼面活荷载。

在1974版规范中，总水平地震荷载表达为Q0=Cα1W，这里引入了结构影响系数C，对于钢框架结构C取值0.25，对于混凝土框架结构C取值0.30。为便于说明，仅考虑反应谱平台段，这时α1=αmax，当设计(设防)烈度为7度、8度、9度时αmax分别取0.23、0.45、0.90。以7度为例，抗震设计时，用于构件强度验算时的地震剪力变成：

Q0=CαmaxW=0.3×0.23W=0.07W

(3)

也就是说，水平地震力的值相当于结构重量的7%。地震剪力与结构重量之比习惯上也称为基底剪力系数。显然，式(3)表征的地震剪力值与现行规范(GB 50011-2010)相当。现行规范指出，多遇地震(小震)作用下结构截面抗震验算的结构总水平地震作用标准值(7度)为

FEk=αmaxGeq=0.08Geq

(4)

8度、9度也类似，可见，规范地震荷载取值没有大的改变，但是技术途径却有很大不同。1974版规范认为，式(1)确定的地震力是基于结构为弹性假定得出的，而结构遭受地震作用时，构件一般表现出一定的塑性耗能特性，动力放大减小，不同结构类型耗能特性略有差异。结构系数C就是要考虑这一影响而把地震力进行折减。而基于概率理论的1989版和2010版规范处理方法截然不同，对于7度区，考虑放大效应后地震剪力为FEk=2.25×0.1Geq=0.23Geq这与式(3)中1974版规范不考虑折减的结果相同，这就造成很大的矛盾，设防烈度相同，地震力相差近三倍。按照图 3所示的概率分布曲线，把设防烈度7度折减到5.45度，地震力幅值减少到三分之一，变成FEk=1/3×2.25×0.1Geq=0.08Geq，这就与1974版规范相当了。

简而言之，虽然经过百余年的发展沿革，地震作用的取值经历了确定性的静力法、动力法及基于概率理论的动力法的演变，但是烈度基准及同一烈度下结构地震作用的取值基本没有改变，把握了这一点，就不容易混淆了。

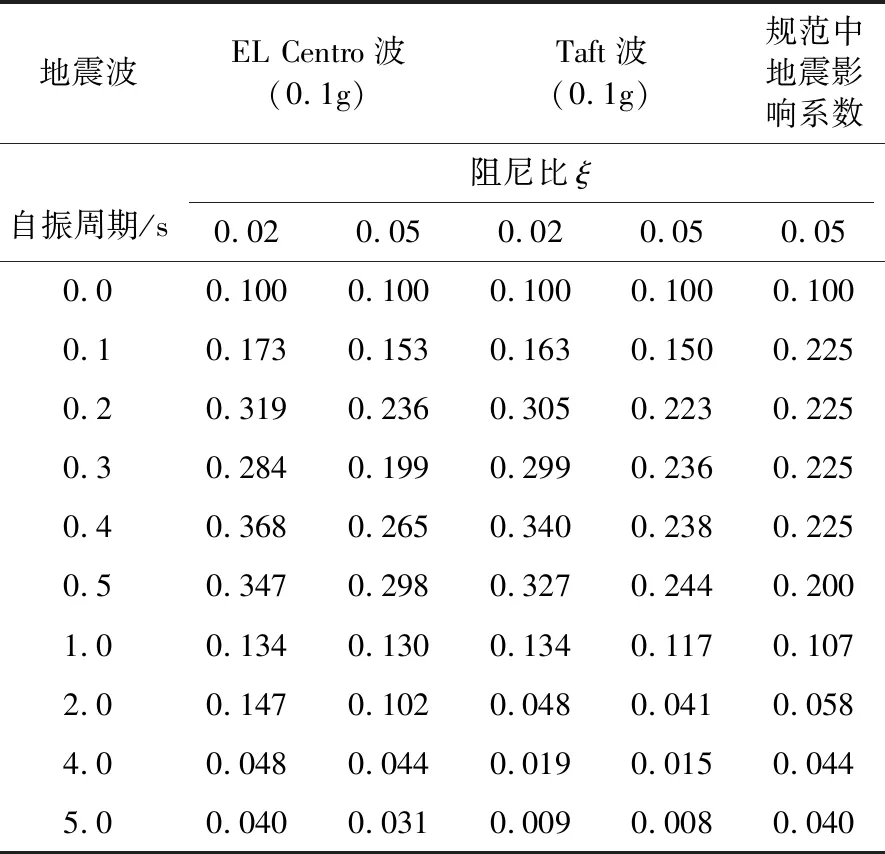
表 3 基底剪力系数的对比Tab.3 Comparison of base shear coefficients

3 地震动参数选取案例分析

结构抗震分析中最常用的实际地震波包括El Centro波和Taft波，如图 1所示。笔者将用反应谱来展示两个实际地震波对应的基底剪力系数并与规范给定的地震影响系数做对比。

图 5 典型地震动的地震影响系数及其 与设计反应谱的对比Fig.5 Seismic influence coefficientn of typical ground motion and its comparison with design response spectrum

将El Centro和Taft地震波按比例将峰值换算成0.10g(相当于7度)，当阻尼比分别为2%和5%时计算的反应谱值列于表 3，对应5%阻尼比的值绘于图 5。取场地特征周期为0.45s，按照规范计算7度中震对应的反应谱也绘于同一坐标系下。从表 3和图 5可以看出，当结构周期在1.0s以内时，地震剪力放大明显，特别是结构周期介于0.20～0.60s时，放大最明显，这时对应的普通民用建筑层数为3～8层。对应7度设防水平，结构受到的地震剪力相当于结构自身重量的20%～30%，如果考虑结构塑性耗能或者折算到7度对应的小震，地震剪力又回到10%左右，这与百年前大森房吉等用简单的基于刚性假定的静力法相当。当结构周期超过2.0s时(30层以上的剪力墙结构)，结构基本周期对应的基底剪力系数比对应的地震系数的一半还小。

4 案例分析

作为参数选取的案例，探讨一下超越概率的使用范围，这也是在工程实践当中很容易混淆的问题。我国当前有十几个地震模拟振动台正在设计或建造中，有一个重要问题需要解决，那就是怎样确定振动台厂房的抗震设防烈度。显然，振动台台面不但给被试验对象-结构模型施加地震力，还通过作动器将反作用力施加给振动台基础。通常振动台的基础也作为厂房的基础。比如，实验时传给基础的地震动峰值为0.1g，一年至少进行几十次这样的实验，厂房“频繁”遭遇强度为0.1g的地震动，按照超越概率理论， 0.1g显然满足小震的频度，那么设防烈度应该是小震的3倍，即0.3g，这对大多数地区都是挑战。这样的理解是错误的。

现行结构荷载规范将荷载分为永久荷载、可变荷载和偶然荷载三类，地震属于偶然荷载，假定其大小符合极值Ⅲ型分布(这就是超越概率的具体体现)，并具有极大的不确定性。振动台运行时的反作用力传给厂房，尽管形式上相当于地震作用，但是这种荷载具有明确的概率分布规律，其上限是明确的，一般不超过0.1g[10]，不存在超越概率的问题，因而可以视为可变荷载(与一般活荷载类似)参与荷载组合，其效果与锻锤的动力影响类似。因此，厂房的抗震设防仍然可以按照其所在地地震动参数区划图规定的设防烈度执行。

5 结论与建议

引入概率理论后，同一设防烈度对应多个表征地震强弱的参数，不容易准确把握。如果把握了地震力取值的发展过程，把握其中不变的核心并考虑规范的沿革并未打破地震力取值的连续性，理解起来就容易得多。早期地震力取值依据确定性理论，只要建设场地的烈度确定，其对应的地震力就唯一确定； 引入超越概率概念后，同一烈度对应三个等级的加速度峰值，峰值越大对应的超越概率越小，此外还引出关联的小震和大震的地震影响系数。

近20年来，全球获取了几万条高质量强震记录，大大丰富了人们对地震动的理解。比如，地震动的不确定性比原来预想得更强，远非极值Ⅲ型概率密度函数所能描述。2008年汶川地震中获得了近1.0g的地震记录，同时有多处迹象表明地震动强度超过1.0g； 2011年日本 3·11 地震时有3个站获得超过2.0g的地震记录。尽管地震动如此强烈，即便是极震区也有大量房屋顽强地“站立”，一部分破坏轻微。事实说明，结构抗震设计是难以定量操作的，正如某知名教授所言“结构抗震七分靠概念，三分靠计算”。只要抗震概念把握得好，实现房屋抗震“七级不坏、八级不倒”[11]并非难事。