地震作用下反倾向层状岩质边坡弯曲倾倒稳定性分析

2022-08-30苏立君徐兴倩娄高中

长江科学院院报 2022年8期

屈新，苏立君，徐兴倩，吕谦，娄高中

(1.安阳工学院土木与建筑工程学院，河南安阳 455000； 2.中国科学院水利部成都山地灾害与环境研究所，成都 610041； 3.云南农业大学水利学院，昆明 650201)

1 研究背景

倾倒破坏是(似)层状岩体边坡常见的一种破坏模式，在自然边坡和工程边坡中均有发生，其中，在反倾向层状边坡中最为常见。然而，由于人们对反倾向边坡的认识的局限性(反倾向边坡的坡体结构属于相对稳定的类型)，该类边坡一直未能引起人们的重视，直至大量反倾向边坡倾倒破坏现象被逐渐揭露[1]。频繁发生的倾倒失稳事故不仅严重制约了工程结构的施工安全及后期的正常运营，而且也严重威胁着人们的日常生活和生命财产安全[2-4]。

为了解决此类工程地质问题，大量专家学者投身到反倾向层状边坡的稳定性分析当中，目前已取得了显著的成果[5-9]。已有研究表明，反倾向层状边坡的失稳破坏常常与人类工程活动、自然灾害密切联系在一起，比如采矿、修筑公路、地震或者不适宜的生活活动等[10-11]。为了探究地震荷载对反倾向层状边坡倾倒稳定性的影响规律，大量专家学者对此问题开展了深入研究。刘才华和陈从新[12]基于传递系数的概念，提出了地震作用下反倾向层状边坡块体倾倒破坏的分析方法，并得出当地震影响系数小于其临界值时，边坡发生倾倒破坏，否则边坡发生滑动破坏。李春生[13]结合FLAC软件和振动台试验探讨了含软弱夹层反倾向岩质边坡地震响应规律和变形破坏机理，并得出坡面放大效应影响因素之间的关系：坡高>坡角>软弱夹层倾角、厚度和位置。刘云鹏等[14-15]详细探讨了地震作用下反倾向边坡岩层破坏区域的分布特征，即沿最大弯折带及坡脚处发生剪切破坏，而在坡体浅表部，尤其是坡缘部位，主要表现为张拉破坏。郑允等[16]针对岩块长细比较大的情况，推导了地震作用下岩块极限平衡微分方程，分析了地震作用下反倾向边坡的块体倾倒破坏模式以及块体倾倒稳定性的影响规律。吴丹妮[17]以石大关梯子槽斜坡作为研究区，通过数值模拟和监测资料反演的手段，得出了地震作用下反倾向边坡影响边坡稳定性的主控因素之间的关系：持时>幅值>坡角>倾角>频率>坡形系数(CSF)。

上述研究充分考虑了地震荷载对反倾向边坡块体倾倒破坏的影响，却鲜有涉及地震荷载对弯曲倾倒破坏的影响研究(当前关于弯曲倾倒破坏的研究多只考虑了自重作用的情形)，地震荷载对反倾向边坡弯曲倾倒稳定性的影响规律尚不清楚。此外，在采用理论分析方法进行反倾向边坡弯曲倾倒稳定性分析时，通常需要将层间相互作用力简化为集中力，但集中力的作用位置是随着层间分布力的变化而变化的，不应该是一个常量。

为了解决上述问题，本文提出一种分析地震作用下反倾向层状边坡弯曲倾倒稳定性的极限平衡方法，该方法认为边坡发生破坏时，坡体内部应力达到极限平衡状态，即基于边坡破坏面计算得到的坡脚岩层剩余下滑力(倾倒力)为0。基于静力等效替代思想，推导了层间力分布形式和推力线高度的计算公式。基于严格的力学推导确定岩层的稳定区域、破坏区域及破坏区岩层的破坏模式，并通过逐步迭代的方式计算坡脚剩余下滑力(倾倒力)。最后，选用皖南板岩边坡作为工程实例验证本文方法的有效性，并探讨地震荷载对该边坡稳定性的影响规律。

2 地质几何模型

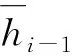
(1)

图1 反倾向层状边坡地质几何模型Fig.1 Geological geometric model of countertendency layered slope

基于已有弯曲倾倒破坏研究的分析结论[18-20]，采用以下几条假设来简化弯曲倾倒破坏的分析过程：

(1)各个岩层的厚度相等。

(2)相邻岩层界面满足极限摩擦平衡条件。

(3)在临界破坏状态，潜在破坏岩层沿边坡破坏面处于极限平衡状态。

3 层间力作用位置的推导

采用理论分析方法进行反倾向层状边坡的弯曲倾倒稳定性分析时，通常需要将层间作用力简化为集中力。对于层间力的作用位置，即推力线高度χ，不同学者得出了不同结论：Aydan和Kawamoto[18]结合底摩擦试验和理论分析方法，发现层间力作用在接触边界的中点处，即χ=0.5。Zheng等[5]采用通用离散单元法(Universal Distinct Element Code，UDEC)软件验证了Aydan和Kawamoto的结论的合理性。Adhikary等[19]将离心机试验破坏数据和理论分析结论进行对比研究，得出χ=0.6。屈新等[6]、郑允等[20]、Qu和Diao[3]从理论分析的角度进一步验证了Adhikary等的结论。然而，各个层间作用力的分布情况并不相同，推力线高度χ并不是一个常量，而是随着层间分布力的变化而变化。推力线高度χ的详细推导过程如下：

平面半无限边坡如图2所示，距离坡顶高度为Li的岩层i其顶部承受的竖向荷载GS为

GS=γLi。

(2)

式中γ为岩层重度。

(3)

式中：n为岩层总数；ntp为坡顶岩层编号。

依据坡面几何条件和静力平衡条件可知，坡面A点(岩层i的顶部)的竖向卸荷荷载G′S为

G′S=γLisinβ。

(4)

图2 平面半无限边坡示意图Fig.2 Schematic diagram of plane semi-infinite slope

岩层i的顶部侧向压力σS为

σS=k0γsin2β。

(5)

式中k0为侧压力系数。

岩层i的底部侧向压力σH为

(6)

于是，岩层i的层间力分布情况如图3(a)所示，将层间分布力等效替换为集中力后，其等效结果如图3(b)所示。图中Pi、Pi-1分别为岩层i受到岩层i+1、i-1的法向推力。

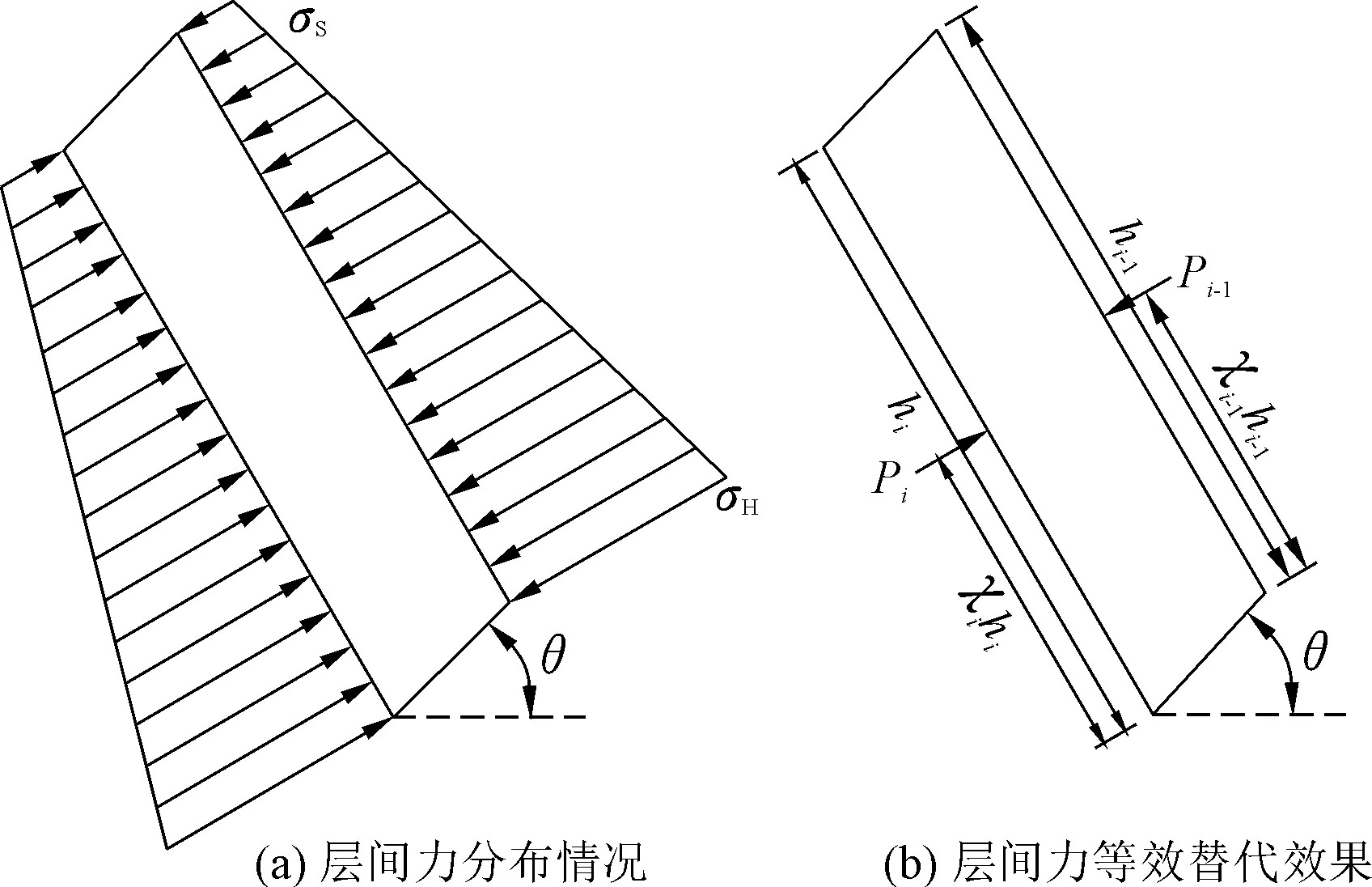
图3 层间力分布情况及等效替代效果Fig.3 Distribution of interlayer interaction force and its static equivalent substitution effect

那么，岩层i的推力线高度χi的表达式为

4 地震作用下反倾向层状边坡弯曲倾倒稳定性分析

4.1 基本思路

野外观测数据[20]显示，由柔性岩体组成的反倾向层状边坡弯曲倾倒破坏面是位于岩层法平面上方的直线型平面。边坡发生破坏时，坡体内部应力达到极限平衡状态，即基于此破坏面计算得到的坡脚岩层剩余下滑力或者倾倒力为0。由于计算机的精度有限，并不能完全保证搜索角θj取值的连续性，导致未必存在某个θj使得边坡剩余下滑力或者倾倒力为0，只可能让坡脚剩余下滑力或者倾倒力尽可能地逼近于0。显然，上述问题实质上是一个最优化问题，即

(8)

式中：Pn是坡脚岩层发生剪切滑移破坏时的剩余下滑力；Tn是坡脚岩层发生弯曲拉裂破坏时的剩余倾倒力；fj(θj)为Pn、Tn两者中的大者；F为fj(θj)绝对值的最小值；nn是搜索次数，本文取为106。搜索角θj可由式(9)确定，即

θj=jΔθr。

(9)

其中，Δθr=β0/nn。

4.2 确定坡顶稳定区域

(10)

(11)

其中，β1=η+θ0。

野外观测发现，坡顶岩层易发生弯曲倾倒破坏[21-22]。对于坡顶第一块发生弯曲倾倒破坏的岩层，由于其不受到其上部岩层的作用力，而下部岩层仅提供抵抗力，所以此岩层发生破坏只可能是岩层重力和地震荷载导致的。若岩层在自重和地震荷载作用(下部岩层作用力为抵抗力)下发生弯曲倾倒破坏，那么位于破坏面上部的等效高度hi必定大于岩层在自重和地震荷载作用下的极限高度h0。h0的表达式为

b(cosα-ksinα))/[6(sinα+kcosα)] 。

(12)

式中σt为岩层抗拉强度。坡顶最后一块稳定岩层的编号nc可通过式(13)确定，则坡顶稳定区域为岩层1—岩层nc。

(13)

4.3 确定潜在破坏区岩层的破坏模式

由4.2小节可知，边坡的潜在破坏区域为岩层nc+1—岩层n。根据野外观测、试验研究、数值模拟和理论分析发现，反倾向层状边坡岩层的破坏模式为剪切滑移破坏和弯曲拉裂破坏[17-18]。对于破坏区任意岩层i，若其发生剪切破坏，则必定满足摩尔-库伦准则，即

τ=σtanφ+c。

(14)

式中：τ为切应力；σ为正应力；φ为内摩擦角；c为黏聚力。

如图4所示，对岩层i进行受力分析，则其底面的切向力Si和法向力Ni分别为：

Si=wisinθ+kwicosθ+Qisinθj+Picosθj-

Qi-1sinθj-Pi-1cosθj；

(15)

Ni=wicosθ-kwisinθ+Qicosθj-Pisinθj-

Qi-1cosθj+Pi-1sinθj。

(16)

式中：wi为岩层i位于破坏面上部的重力；Qi为岩层i与岩层i+1之间的摩擦力；Qi-1为岩层i与岩层i-1之间的摩擦力。

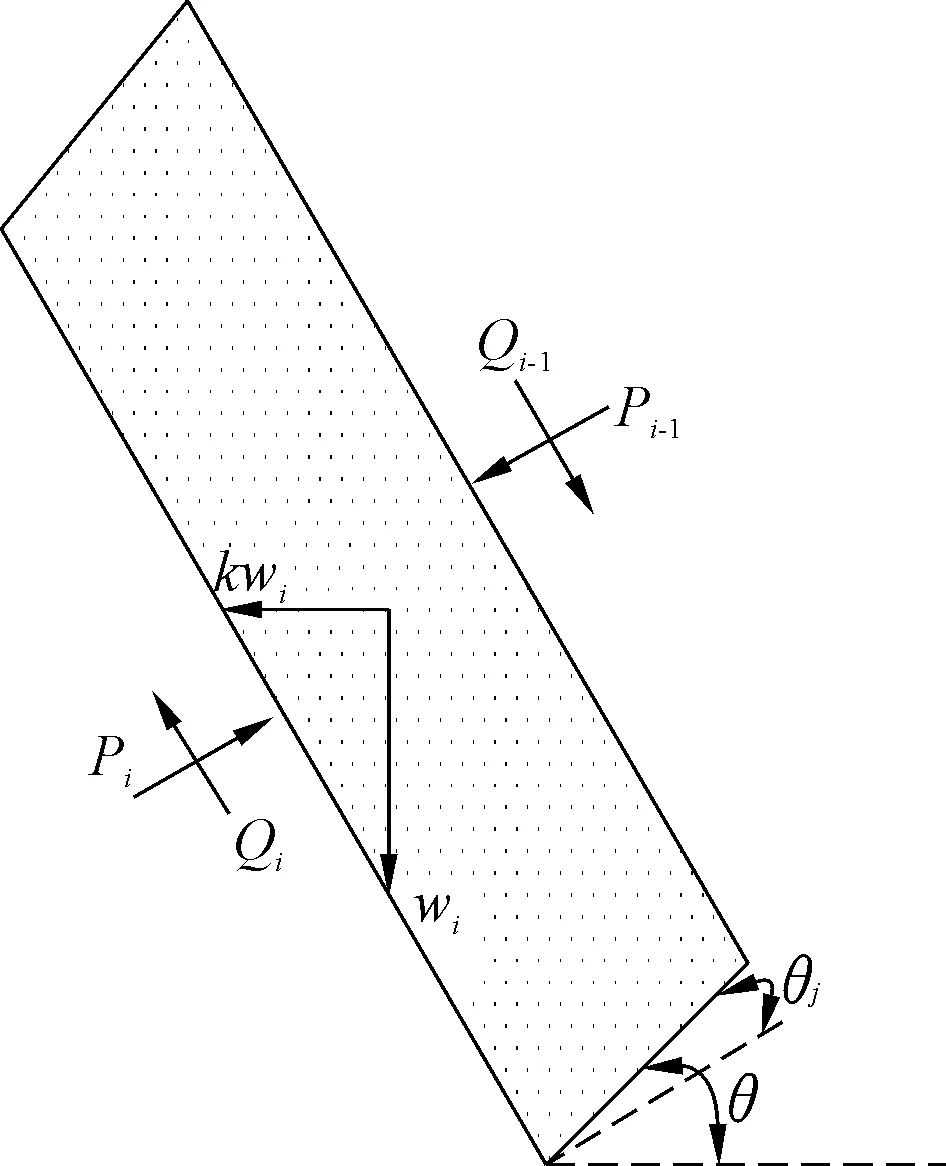
图4 岩层i剪切破坏受力分析Fig.4 Force analysis of stratum i for shear failure

相邻岩层之间满足库仑摩擦定理，即

Qi=Pitanφi，Qi-1=Pi-1tanφi。

(17)

式中φi为层间内摩擦角。

于是，Pi可表示为

Pi=[max(Pi-1，0)-(cosθ(tanφ-tanθ-

k-ktanθtanφ)wi+cb/cosθj)]/

[(1+tanφitanθj)cosθj]+tanφcosθj·

(tanθj-tanφi) 。

(18)

若岩层i发生弯曲拉裂破坏，则必定满足最大拉应力理论，根据材料发生组合变形(弯曲变形和轴向压缩变形)时拉压应力的计算公式，有

(19)

式中：Mi为岩层i底面的弯矩；I为惯性矩；Ni为岩层i底面的轴力；σmax为最大拉压应力。

如图5所示，岩层i发生拉破坏，则弯矩和轴力分别为：

(20)

Ni=wicosα-kwisinα+Qi-Qi-1。

(21)

式中：Ti为弯曲拉裂破坏时岩层i受到岩层i+1的法向推力；Ti-1为弯曲拉裂破坏时岩层i受到岩层i-1的法向推力。

图5 岩层i弯曲拉裂破坏受力分析Fig.5 Force analysis of stratum i for tension failure

相邻岩层之间满足库仑摩擦定理，即

Qi=Titanφi，Qi-1=Ti-1tanφi。

(22)

于是，Ti可表示为

(23)

对岩层i而言，若Pi≥Ti，即岩层i发生剪切破坏时向下部岩层传递的剩余下滑力大于其发生弯曲拉裂破坏时向下部岩层传递的剩余倾倒力，那么岩层i发生剪切破坏所需的上部推力小于发生弯曲拉裂破坏所需的上部推力，此时岩层i将发生剪切破坏；反之，岩层i将发生弯曲拉裂破坏。

在计算过程中，如果出现max(Pii，Tii)<0(nc+1≤ii≤n)，那么岩层nc+1—岩层ii将不会发生破坏，岩层ii与ii+1之间的相互作用力为0。如果max(Pii，Tii)>0，那么岩层nc+1—岩层ii会发生破坏，岩层ii与ii+1之间的相互作用力为max(Pii，Tii)。稳定区岩层1—岩层nc之间的相互作用力满足Pi=Ti=0(1≤i≤nc)，再根据式(18)和式(23)，确定坡脚剩余下滑力或者倾倒力max(Pn，Tn)。

4.4 确定边坡剩余下滑力、破坏面和稳定系数

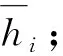
按照式(24)同步折减岩体强度参数(黏聚力c、内摩擦角φ、层间内摩擦角φi、抗拉强度σt)使边坡剩余下滑力(倾倒力)F等于0，此时对应的折减系数Fs即为边坡的稳定系数。

(24)

式中：c′、φ′分别是折减后的黏聚力和内摩擦角；φi′是折减后的层间内摩擦角；σt′是折减后的抗拉强度。

5 算例分析

5.1 皖南反倾向板岩边坡

选取皖南反倾向板岩边坡[22]作为本文的工程实例。根据文献[22]，边坡参数如表1所示，反倾向板岩边坡破坏示意图如图6所示。

表1 皖南反倾向板岩边坡计算参数

图6 皖南反倾向板岩边坡示意图Fig.6 Schematic profile of slate slope in south Anhui

基于本文的计算方法，不同岩层间的推力线高度如图7所示，皖南反倾向板岩边坡发生弯曲倾倒破坏，边坡破坏面位于岩层法平面上方10.05°。稳定区域为岩层1—岩层8(图8)，破坏区域为岩层9—岩层400，其中弯曲拉裂破坏区为岩层9—岩层384，剪切破坏区为岩层385—岩层400。边坡稳定系数为0.735 2，收敛曲线如图9所示；边坡剩余下滑力为1.926 6×107N(表2)。采用Aydan 和Kawamoto[18]的方法求得的稳定系数为0.664 4，边坡剩余倾倒力为3.803 2×107N，岩层破坏总数为400，即所有岩层全部发生弯曲倾倒破坏。采用郑允等[21]的方法计算得到的稳定岩层为岩层1—岩层21，岩层387—岩层400发生剪切破坏，其余岩层全部发生弯曲倾倒破坏。上述3种方法得到的皖南板岩边坡破坏面如图10所示。

图7 不同岩层间的推力线高度Fig.7 Non-dimensional height of the point of application of normal force among different strata

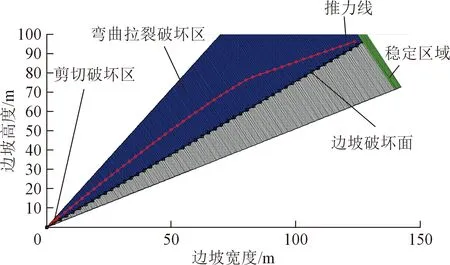
图8 皖南板岩边坡破坏区域、破坏面及不同岩层间的推力线位置Fig.8 Failure plane and failure zones of slate slope in south Anhui and the point of application of normal force

图9 皖南反倾向板岩边坡稳定系数收敛曲线Fig.9 Convergence curves of stability coefficient of slate slope in south Anhui by different methods

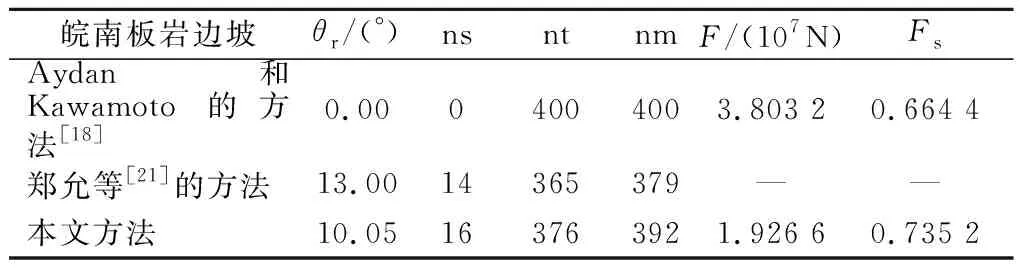
表2 皖南板岩边坡计算结果对比

图10 不同方法得到的皖南反倾向板岩边坡破坏面Fig.10 Slope failure planes of slate slope in south Anhui by different methods

Aydan和Kawamoto[18]认为边坡破坏面是岩层法平面，但事实上在岩层破坏发育深度达到其法平面之前边坡已经发生了整体性破坏，并且他们忽略了坡脚岩层发生剪切破坏的可能性，因此，他们高估了边坡的稳定性。郑允等[21]的计算方法忽略了部分坡顶稳定岩层，因为只有当坡顶岩层位于破坏面上部等效高度大于极限高度时，岩层才会发生破坏，所以，他们的计算方法低估了边坡的稳定性。此外，Aydan和Kawamoto[18]、郑允等[20]的计算方法将不同岩层间的推力线高度视为常数，显然与实际情况不符，并且他们高估了推力线高度。综上，本文得到的皖南反倾向板岩边坡破坏面及稳定系数是合理可信的。

5.2 地震作用对反倾向边坡稳定性的影响

以上述皖南反倾向板岩边坡为工程案例，研究地震荷载对反倾向边坡稳定性的影响。当地震影响系数k分别取0、0.1、0.2、0.3和0.4时，破坏角θr、剪切破坏岩层数目ns(剪切破坏区域)、弯曲拉裂破坏岩层数目nt(弯曲拉裂破坏区域)、岩层破坏总数nm(边坡整体破坏区域)、坡脚剩余下滑力F和边坡稳定系数Fs的数值列入表3，变化规律见图11、图12。

根据表3和图10—图11可知：

(1)当地震影响系数k为0、0.1、0.2、0.3和0.4时，坡脚剩余下滑力都>0，稳定系数<1，说明边坡处于失稳状态，将发生弯曲倾倒破坏。并且随着地震影响系数的增大，边坡稳定系数减小，坡脚剩余下滑力增大，说明边坡越不稳定。

(2)随着地震影响系数的增大，破坏角增大，边坡破坏面向坡面上移，破坏岩层的发育深度变浅，说明边坡孕育变形破坏时间缩短，此时，边坡容易发生浅层破坏。

(3)随着地震影响系数的增大，剪切破坏岩层数目增多(剪切破坏区域扩大)，弯曲拉裂破坏岩层数目和岩层破坏总数减小(弯曲拉裂破坏区域和浅层破坏区域缩小)，破坏岩层的发育深度变浅，边坡可能会进一步发生多级破坏。究其原因是，地震影响系数的增大导致边坡孕育变形破坏时间缩短，容易发生浅层破坏，岩层位于破坏面上部高度减小，岩块长细比减小，岩层抗倾倒能力增加，此时岩层更容易发生剪切破坏，故剪切数目增多，弯曲拉裂破坏岩层数目和岩层破坏总数减小。

表3 皖南板岩边坡稳定性参数随地震影响系数变化情况

图11 皖南板岩边坡稳定系数收敛曲线随地震影响系数变化情况Fig.11 Convergence curves of stability coefficient of slate slope in south Anhui with the change of seismic coefficient

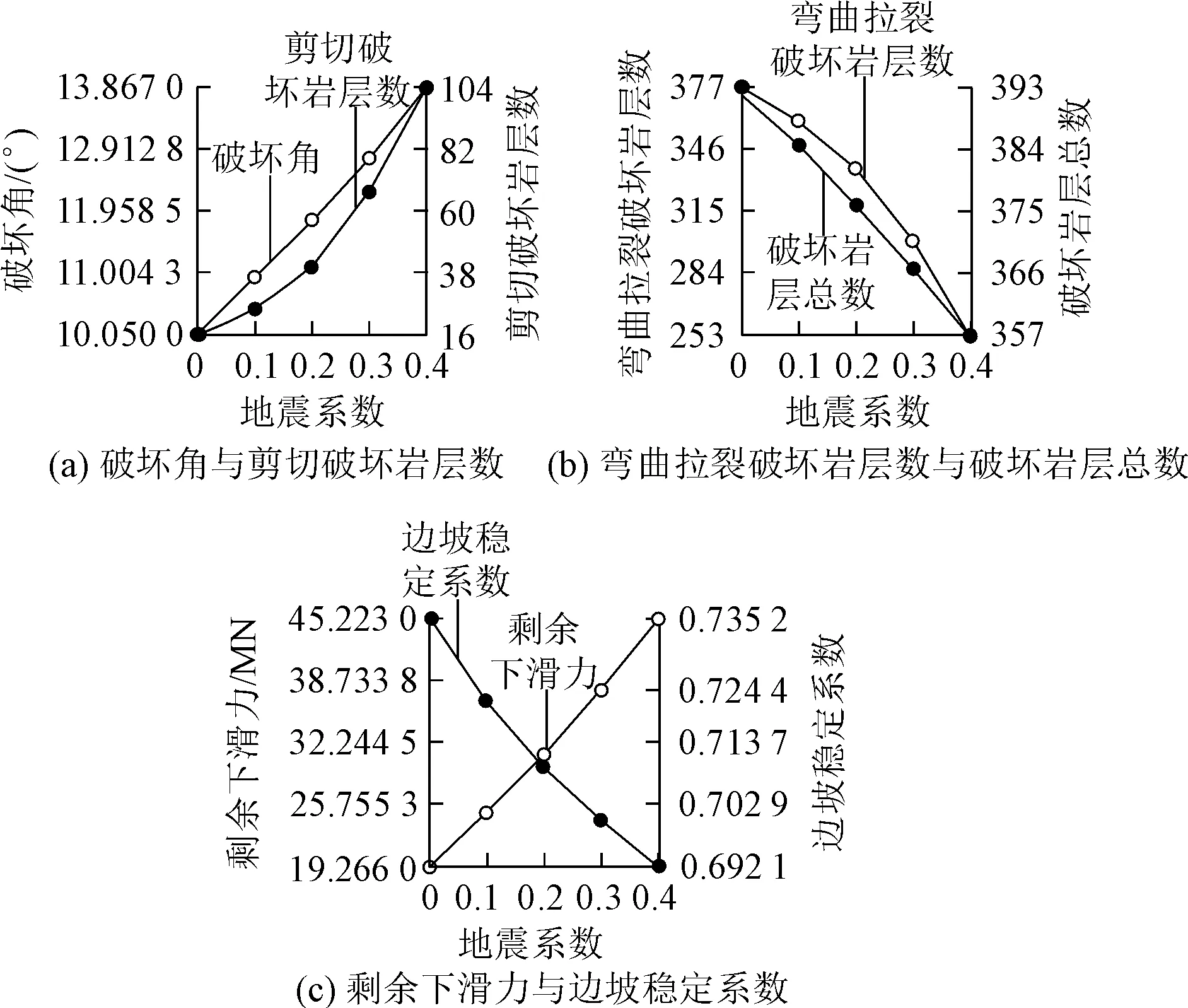
图12 不同边坡参数随地震影响系数变化情况Fig.12 Different parameters of slate slope in south Anhui with the change of seismic coefficient

6 结论与展望

6.1 结论

本文提出了一种分析地震作用下反倾向层状边坡弯曲倾倒稳定性的极限平衡方法。该方法将整个边坡分为稳定区、弯曲拉裂区和剪切破坏区，详细推导了层间力分布形式，修正了不同岩层的推力线高度；基于严格的力学推导确定了不同岩层的破坏模式，并采用最优化的思想确定了边坡破坏面。最后结合工程实例证明了本文方法的有效性，探讨了地震荷载对该边坡稳定性的影响规律。结果表明：随着地震影响系数的增大，破坏角、剪切破坏岩层数目和坡脚剩余下滑力增大，而弯曲拉裂破坏岩层数目、岩层破坏总数和边坡稳定系数减小，边坡更容易发生浅层破坏，变得更不稳定。