闭环控制DC/DC变换器带恒功率负载的稳定性研究

尹英龙，刘宝泉

（陕西科技大学 电气与控制工程学院，西安 710021）

在直流微电网中，电力电子变换器在电力系统的大规模应用［1-3］，给电力系统引入了大量非线性负载，对电力系统的稳定性产生诸多不利影响［4］。恒功率负载作为一种典型的非线性负载［5］，在DC/DC分布式系统以及大部分直流微电网的场景中占有越来越大的比例，尤其是当闭环控制的多个电力电子变换器级联时，后级通常可以等效为前级的恒功率负载。

目前的稳定性研究以小信号扰动为主，利用小信号分析方法可以忽略系统中微小的非线性因素，对建立的模型线性化处理从而推导出稳定性判据，能够解决平衡点附近的稳定性问题［6］，但恒功率负载和电力电子变换器自身特性给系统带来的非线性不可忽略。为了寻求对含恒功率负载的系统进行有效控制的方法，对其进行大信号下的稳定性分析尤为重要。在直流微网中，大信号稳定性是指系统受到大扰动时系统的稳定性［7］，例如起动、负载突变以及系统中有非线性负载等工况［8-9］。

目前，针对大信号的稳定性分析主要有两种方法，一是Lyapunov特征值法估计，将原系统状态方程线性化后，通过系统雅克比矩阵的特征值来判断系统在平衡点的稳定性，当特征值均有负实部时，该系统在平衡点处稳定，但该方法涉及多维矩阵的复杂计算，不便于实际的操作。第二种方法是利用混合势函数理论，它是一种基于Lyapunov直接法的特殊分析方法［10］，根据系统中元器件的能量关系，列写能量方程，进一步计算出解析形式的稳定性判据。在电力系统中基于这一方法研究人员开展了大量工作并得到了诸多成果。文献［11］利用混合势函数结合验证了无源控制下的燃料电池-超级电容器（FC-UC）系统的稳定性。文献［12］利用混合势函数对三相PWM整流器级联DC/DC变换器系统（双闭环系统）进行了大信号分析，得到大扰动下的稳定边界（不等式），并进行了简单的仿真验证。文献［13］使用混合势函数推导了下垂控制的含CPL和LC滤波器的直流系统稳定性判据，并通过仿真验证了该判据的有效性。文献［14-16］利用混合势函数理论分析了开环控制的电力电子变换器在大信号扰动下的稳定边界，得到了解析形式的稳定性判据，为系统的设计提供了准则。文献［17］利用混合势函数理论对直流微电网级联系统中恒功率负载和储能单元充放电功率参数对稳定性的影响进行研究并得到了稳定性判据。文献［18-19］将级联系统中负载变流器等效为恒功率负载，基于回转器理论建立DC/DC变换器统一的大信号模型，并推导了基于该模型的混合势函数稳定性判据，定量地分析了控制器参数对电流控制型BUCK/BOOST变流器稳定性的影响。文献［20-22］利用混合势函数的方法建立了双级LC滤波器和4种阻尼滤波器的系统大信号模型，并推导各种滤波器对大扰动下的稳定性的影响。文献［23］假设电流内环跟踪电压外环实时变化，简化了电压电流双闭环的等效电路并在此基础上利用混合势函数方法分析稳定性并得出稳定性判据。

当前研究主要以开环为主，而闭环控制型（VMC）的电力电子装置还没有过多的涉及。本文以BUCK变换器为研究对象，控制方法采用电压电流双闭环，控制器选用比例积分控制器，建立了大信号平均模型，列写了系统的混合势函数，得到了大信号稳定的充分条件；进一步利用这一条件设计系统参数，得到渐进稳定域；并通过构造能量函数，利用Lyapunov稳定性判据验证了稳定域的存在性。最后，通过仿真验证了所求稳定运行条件的合理性。

1 闭环控制BUCK电路的大信号模型

根据图1所示BUCK电路的简化结构，设占空比为D，恒功率负载功率为P0，输入电压为U1可以得到BUCK电路带CPL状况下的大信号平均模型：

BUCK电路采用电压电流双闭环控制，设电压外环的比例系数kvp，积分系数kvi，参考电压为vref，电流内环的比例系数kip，积分系数kii，PWM比较器配置锯齿波幅值vs=1，电路如图2所示。

图1 BUCK变换器简化电路图

图2 带CPL的双闭环控制BUCK变换器电路图

电压电流双闭环控制建立了电感电流与占空比的关系，有

根据电压环和电流环的连接关系，有

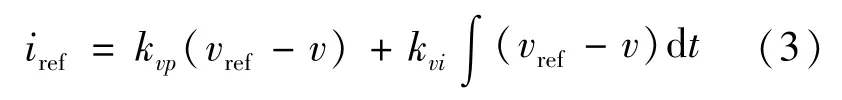
则电压闭环控制的占空比D可以表示为

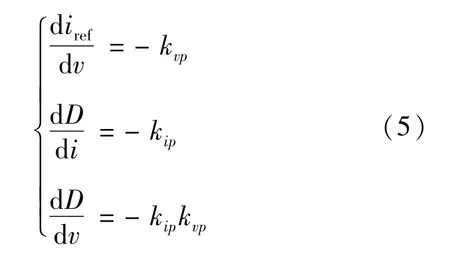
则电压电流双闭环控制下的占空比D可以改写为：

2 闭环控制BUCK 电路的混合势函数模型

2.1 混合势函数理论概述

1964年R.K.BRAYTON和J.K.MOSER提出了一种非线性网络的理论，这是混合势函数理论首次用于电力系统的稳定性分析。这种方法从能量的角度出发，结合Lyapunov稳定性分析方法，对满足式（7）的网络求解大信号稳定充分条件及具体的大信号渐进稳定域。

首先要列写电路的混合势函数P（i，v），它是由电流势函数A（i）、电压势函数B（v）以及由于电路拓扑引起的能量变化（i，γv-α）3部分组成，即：

根据式（8），分别求出P（i，v）中电流势函数和电压势函数对电感电流和电容电压的二阶导数Aii和Bvv，进而求解最小特征值λ1和λ2分别为：

由此可以得到系统在大信号扰动下稳定的充分条件为λ1+λ2＞0，设混合势函数关于电感电流和电容电压的一阶偏导数为Pi和Pv，进一步构造Lyapunov能量函数P*（i，v）为

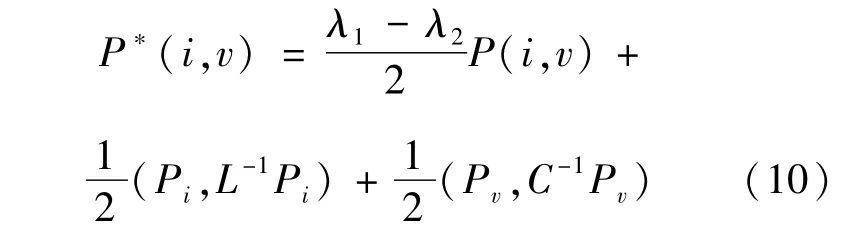
再求出能量函数对时间的导数d P*／d t，利用Lyapunov第二方法，找到使P*正定、d P*／d t负定的区域（i，v），即为系统在大信号下的渐进稳定域。

2.2 闭环控制BUCK变换器的混合势函数

由电路中所有非储能元件可以列写出电流势函数，若元件不能直接写出电流势函数，可以列写电压势函数。图2中所示BUCK电路中所有非储能元件包括电压源U1和恒功率负载CPL。其中恒功率负载的额定功率是P0，则电流势函数可以记作P（i）。

电路中无电阻元件，开关前后的电源可以近似等效为受控电压源，所有非储能元件可以用电流势函数表示：

恒功率负载Po的电流势函数转化为电压势函数：

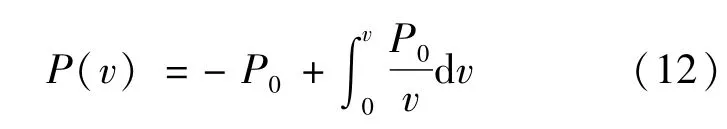
电容C的能量：

混合势函数P（i，v）为式（11）～（13）的和，求和整理后结果如下：

将所列写的P（i，v）代入式（7）检验，混合势函数列写正确。进一步将式（6）代入式（14），即可得到闭环控制的BUCK变换器带CPL的混合势函数：

3 闭环控制BUCK电路稳定性分析

3.1 闭环系统大信号稳定的充分条件

设A（i）、B（v）和（i，γv-α）分别为式（14）中的电流势函数、电压势函数和其他部分，有

设A（i）和B（v）对电感电流的二阶偏导数分别为Aii（i）和Bvv（v），有

设矩阵L-1／2Aii（i）L-1／2和C-1／2Bvv（v）C-1／2的最小特征根为λ1和λ2，有

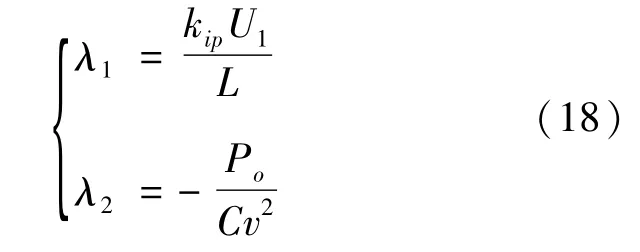
大信号扰动下，要该变换器稳定工作，需要λ1和λ2满足λ1+λ2＞0，即

由恒功率负载的性质，有

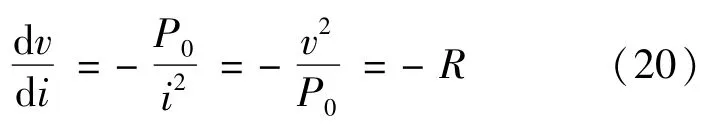
又有系统稳态平衡点为（UL，IL），恒功率负载满足-RL=-UL／IL，则大信号稳定判据式（20）可以改写为

3.2 闭环系统的渐进稳定域

基于式（21）所示的大信号稳定判据，对图2所示系统模型进行参数设计，具体取值如表1所示。

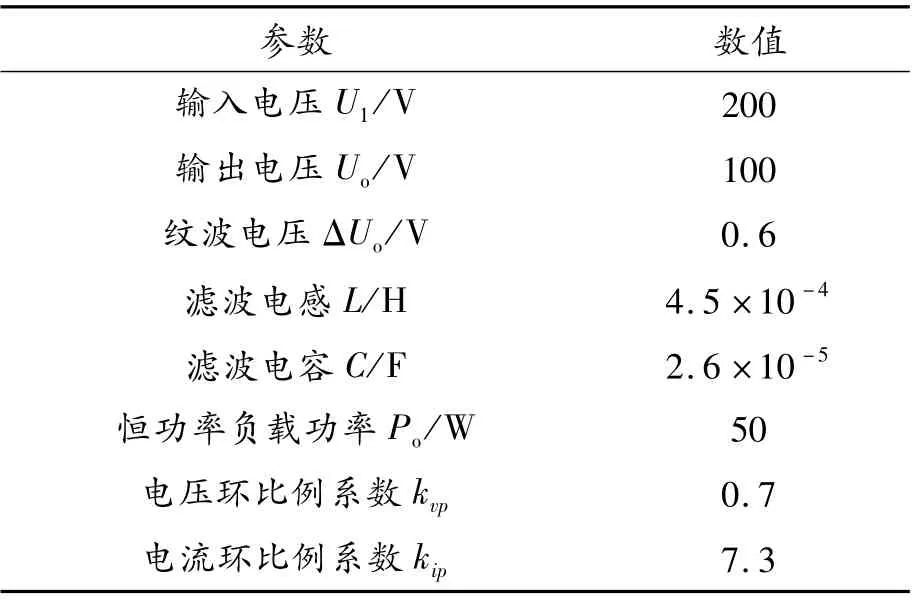
表1 200 V/100 V BUCK电路电压闭环部分参数

根据第2节构造Lyapunov能量函数的方法，先求解Pi和Pv，有

下面构造Lyapunov能量函数P*，并在能量函数的基础上对时间t求导得到d P*（i，v）／d t：

当P*（i，v）正定、d P*（i，v）／d t负定时，可以推得系统的渐进稳定域。以200 V/100 V BUCK变换器为例，把表1的参数代入式（24）（25）中计算，应用Matlab绘图工具分别绘制电压闭环条件下的P*（i，v）及d P*（i，v）／d t随电感电流i、电容电压v的三维曲线图，分别如图3、4所示。

图3 Lyapunov能量函数P*（i，v）三维图

图4 d P*（i，v）／d t三维图

从图中可以看出：存在着同时满足P*（i，v）在P*=0平面以上和d P*（i，v）／d t在d P*／d t=0平面以下2个条件的区域，找到同时满足2个条件的区域在i-v平面上的投影，即为该系统的渐进稳定域。

该系统在进行电能转换时的渐进稳定域可以表示为

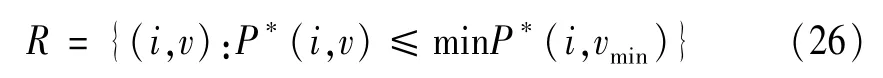
根据式（26），可以绘制系统的渐进稳定域，稳态工作点（100 V，5 A）包含在稳定域中，如图5所示。

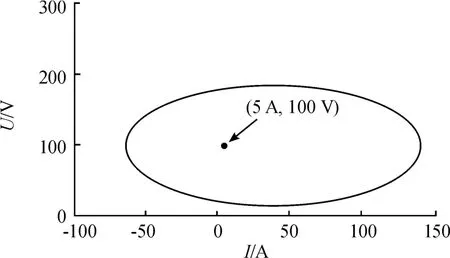
图5 系统渐进稳定域示意图

4 仿真验证

本文主要采用Matlab/Simulink元件库搭建双闭环控制的BUCK电路带恒功率负载仿真模型，具体如图6所示，其中恒功率负载（CPL）模块由含受控电流源单端口的电路模拟。

图6 带恒功率负载的BUCK电路仿真模型

利用表1中的电压电流双闭环控制的BUCK电路系统参数，对所求充分性条件的合理性进行仿真验证，如图7所示。先改变恒功率负载的功率取值，取满足充分条件的两组功率值P0=200 W（图（a））和P0=500 W（图（b）），该系统电压在短暂一段时间振荡后能够稳定在100 V输出；再取超出稳定条件的功率值（P0=5 kW）仿真，如图8所示，系统电压在不断大幅振荡，无法达到给定的输出电压值。

进一步对满足充分条件的系统进行加载实验，验证大信号扰动下系统的稳定性。在带恒功率负载为500 W 和800W 的系统稳定运行后分别突加10Ω的负载，如图9所示，电压值均在加载之后短暂波动，很快恢复到期望的输出电压值100 V，说明恒压负载的大信号扰动下系统能够稳定运行。再对带恒功率负载Po=1 kW 的系统进行负载功率阶跃的仿真，如图10所示，在稳定运行后分别加载至2 kW 和3 kW，电压值在短暂波动后迅速回到100 V，说明在功率突增的大信号扰动下，系统仍能稳定运行。

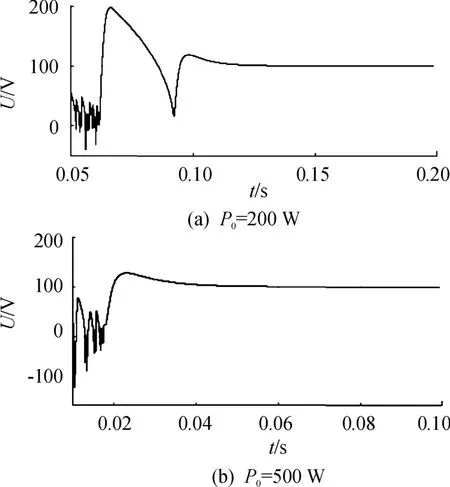
图7 恒功率负载满足充分条件时的电压波形

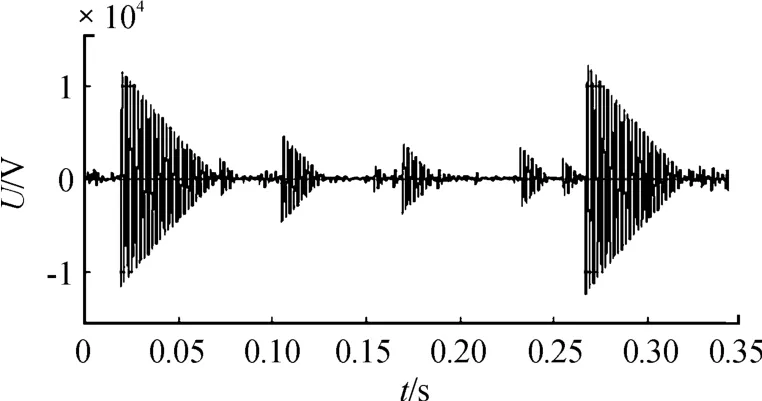
图8 恒功率负载不满足充分条件时的电压波形

图9 稳定运行后突加电阻负载的电压波形

图10 P0=1 kW 稳定运行后突加恒功率负载的电压波形

5 结束语

本文基于大信号扰动的稳定性研究闭环系统涉及不多，以双闭环控制的BUCK变换器带恒功率负载系统为研究对象，利用混合势函数的理论，得到了系统稳定的充分条件。该条件与恒功率负载的负阻抗特性、电流环的比例系数以及系统的电感电容参数均有关，且该条件为系统的参数设计提供了依据。设计的系统可以进一步构造能量函数，通过Lyapunov稳定性判据推导渐进稳定域。该稳定域的存在性表明满足充分条件的系统在大信号扰动下可以稳定运行，仿真验证了该条件的正确性。