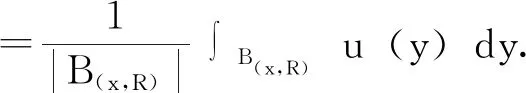偏微分方程均值公式的物理推导

刘 瑞，陈静华

(宜春学院 数学与计算机科学学院，江西 宜春 336000)

拉普拉斯方程[1]，是由拉普拉斯(p.-s. Laplace)在1784年所提出来的，拉普拉斯方程是一种比较典型的椭圆型方程，它具有广泛的应用背景，例如满足此类椭圆型的方程有静电学中的电势。由于此方程是通过势函数的方式来描写了引力场和电场等一些物理对象的性质，所以进行求解Laplace方程是我们在各种特殊领域中常常遇到的一类非常重要的问题[2]。

满足拉普拉斯方程的函数叫调和函数[3]，调和函数在偏微分方程中的运用十分广泛，因为它有很多好的性质。其中一条性质是调和函数满足均值公式，但是在数学里面均值公式的证明非常详细并且繁琐，它是由拉普拉斯方程来的，在数学上有很多的应用，并且被研究得非常透彻，例如在偏微分方程中的应用等。但是很少有人考虑数学里面的均值公式和拉普拉斯方程的物理背景，那么拉普拉斯方程和均值公式具体有什么样的物理意义呢？这就是我们这篇文章所要探讨的，本文从最基本的牛顿万有引力来推导拉普拉斯方程和均值公式。

下面我们引入本文将要出现的一些定义：

定义1 在引力场中有质量为M的物体，某点处单位质量物体所受到的引力为该点的万有引力，记为F，即

其中G为万有引力常数，r为两个物体之间的距离。

定义2 在引力场中有质量为M的物体，某点处单位质量的物体对应的引力势能为该点的引力势，记为U，即

1 符号说明

本文所涉及到的符号作以下说明：

球BR：以R为半径，以原点为球心的球；球：B(x,R)以R为半径，以x为球心的球；球面∂B(x,R)：以R为半径，以x为球心的球面；Rn：n维欧式空间。

2 势函数与拉普拉斯方程

势理论首先建立在力学中，牛顿万有引力定律建立之后，在18世纪，物理学的一个非常重要问题是确定一个物体与另一个物体引力之间的大小。例如：地球与外部质点的之间引力；太阳与行星的之间的引力；地球与另一连续分布物体之间的引力等等。若不能把两个物体都当作质点，就必须要考虑不同物体的形状和质量主要分布的情况。

下面我们从万有引力出发，通过具体公式来看各种情形的势函数的表达式及性质。

2.1 单个质点的势函数

由牛顿万有定律可知，设在P0(x0,y0,z0)点有质量为m0的质点，p(x，y，z)点有质量m的质点，那么质点p与质点p0之间的万有引力为:

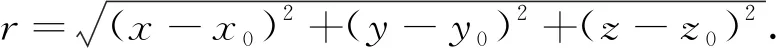
若令

则该质点对处于它周围的质点有引力的作用，该力的大小与质量m成正比，与距离r成反比。

由势函数定义可知，p点引力场的引力势函数为:

那么，引力与引力场的势函数有如下关系

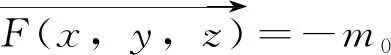
所谓说势函数是指把一个物体放在某个场里面，这个场就会对这个物体产生吸引力或排斥力，并且这个场在不同的位置产生的吸引力或排斥力也不同。

定理1 拉普拉斯发现，若p(x，y，z)是一个孤立的点，则其对应的势函数u(x，y，z)为调和函数，即

Δu(x，y，z)=0.

证明：因为

其中G，m是常数，所以

因此，

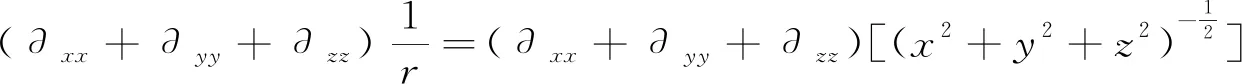
=0.

2.2 多个质点的势函数

若现在考察的质点有许多个，例如在点a1，a2…al处有质量分别为M1，M2…Ml的l个质点，则该l个质点所产生的引力场势函数为:

其中G是重力常数。同理，该势函数也是调和函数。

2.3 连续分布的势函数

如果我们考虑的质点是连续质点，例如它的质量均匀的分布在一个球上，并且质点分布的的密度函数为ρ(x)，则它对应的势函数为:

其中Ω表示连续分布的质点代表的几何图形。此处积分是对y积分，因此求拉普拉斯算子可以证明该势函数也为调和函数。

定理2 在物理上，实际上势函数是把单位质量物体移到无穷远处做的功，即

前面我们已经知道了势函数的各种表现形式，那么对于一些特殊分布的质点它的势函数是怎样的呢？

定理3 单位球的势函数与单个质点的势函数一样，即

(r表示质点到单位球球心的距离)。

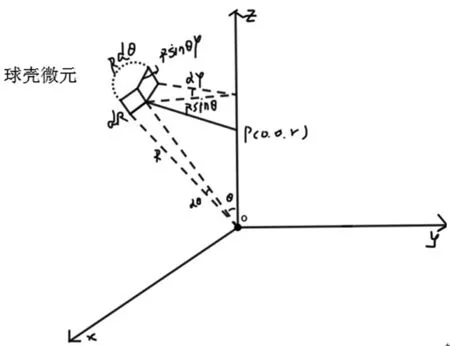
证明：若质点均匀分布在单位球BR上，其总质量为M，如图

令u(x)=u(r)，|x|=r.其中r表示p点到球心的距离，和定理1一样证明，可得

Δu=0.

则

可以发现上式是一个简单的常微分方程，可采用变量分离的方法求解，所以

等同于求解

则

lnu′(r)=-2lnr+c，

两边同时取指数

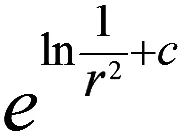
对上式两边取不定积分，则

(1)

又因为

(2)

综合(1)(2)式，则

c=-GM，D=0

即

结论：说明球体物体的势函数与质量成正比，与距离r成反比，即与单个质点的势函数一样。

2.4 球壳外的势函数

定理4 对于一个质量均匀分布的球壳{R1<|x|

证明：略(和定理3一样证明)。

2.5 球壳内的势函数

定理5 对于一个质量均匀分布的球壳{R1<|x|

u(x，y，z)=c.

(其中c为常数)。

证明：如图

设p是球壳内任意一点，我们考虑球壳在p点处的势函数，不失一般性，设p点处的坐标为p(0，0，r)；r

dv=Rsinθdφ·Rdθ·dR，

=R2sinθdφdθdR.

因此，该处的势函数为:

其中

l2=R2+r2-2Rrcosθ.

因此，势函数为：

=(R2-R1)2πGρ(y)R

=c

因为密度均匀分布，ρ(y)是一个常数。

3 均值公式

现在设Ω是Rn上的一个开集，且u是Ω上的一个调和函数，我们将从势函数的角度来推导调和函数的均值公式，它说明函数u在点x∈Ω上的取值u(x，y，z)等于u在球面∂B(x,R)上的平均值，也等于它在球B(x,R)上的平均值。[1]

定理6 假设u是调和函数，并在B(x,R)={y∈Rз|x-y|

则

接下来我们利用势函数

来证明均值公式，为计算方便，设Gm为常数1，令

由定理1可知

Δu(x，y，z)=0.

由上述推导可知，要证明均值公式，即证

也就是要证

也就是需要证明在空间a点处关于单位质量的球面∂B(x,R)的势函数等于在x处单位质量所产生的引力在空间a点处的引力势。

证明：如图

由于空间a点是空间中任意的一点，为不失一般性，则设a点的坐标为(0，m，0)，球面任意一个微元圈的圆心记为E(0，e，0)，由于球的半径为R，则小圆环半径为r=Rcosθ，点a到小圆环圆心E处的距离为d=m-Rcosθ，则

小圆环周长：2πr=2πRsinθ.

小圆环面积：S=2πR2sinθdθ.

点a到球面上的微元圈的距离为：

因此，在空间a点处的势函数为：

因此，定理得证。